Каким свойством обладает мнимая единица

Ìíèìàÿ åäèíèöà — â îñíîâíîì êîìïëåêñíîå ÷èñëî, êâàäðàò êîòîðîãî ðàâíÿåòñÿ îòðèöàòåëüíîé åäèíèöå:  .
.
×èñëî  íàçûâàåòñÿ ìíèìîé åäèíèöåé.
íàçûâàåòñÿ ìíèìîé åäèíèöåé.
Ìíèìàÿ åäèíèöà íå îòíîñèòñÿ ê ïðèâû÷íîìó íàì ìíîæåñòâó äåéñòâèòåëüíûõ ÷èñåë, à èñïîëüçóåòñÿ äëÿ ðàñøèðåíèÿ ýòîãî ìíîæåñòâà.
Ìíèìàÿ åäèíèöà — ýòî ÷èñëî, ó êîòîðîãî êâàäðàò ðàâíÿåòñÿ ìèíóñ åäèíèöå. Òî åñòü i — ýòî îäíî èç ðåøåíèé óðàâíåíèÿ:
 èëè
èëè  .
.
È òîãäà åãî âòîðûì ðåøåíèåì óðàâíåíèÿ áóäåò  , ÷òî ìîæíî ïðîâåðèòü ïîäñòàíîâêîé.
, ÷òî ìîæíî ïðîâåðèòü ïîäñòàíîâêîé.

Êîìïëåêñíàÿ ïëîñêîñòü. Âñå òî÷êè íà ïëîñêîñòè ñîîòâåòñòâóþò êîìïëåêñíîìó ÷èñëó. Êîîðäèíàòû a è b ñîîòâåòñòâóþò äåéñòâèòåëüíîé è ìíèìîé ÷àñòè êîìïëåêñíîãî ÷èñëà.
Ïðèìåðû ðàñ÷åòîâ ñ ìíèìîé åäèíèöåé.
Èíòåðåñíî òî, ÷òî âñå ìíîãî÷ëåíû èìåþò êîðíè, åñëè áðàòü â ðàñ÷åò ìíèìóþ åäèíèöó, åñëè òî÷íåå, êîëè÷åñòâî êîðíåé ðàâíÿåòñÿ ñòåïåíè ìíîãî÷ëåíà, ñ òî÷íîñòüþ äî êðàòíîñòè êîðíåé.
Íàïðèìåð:

Ñòåïåíè ìíèìîé åäèíèöû .
Ñòåïåíè i ïîâòîðÿþòñÿ öèêëè÷íî:










Ýòî ìîæíî çàïèñàòü äëÿ ëþáîé ñòåïåíè òàêèì îáðàçîì:

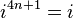


ãäå n — âñÿêîå öåëîå ÷èñëî.
Îòñþäà:  , ãäå mod 4 ýòî îñòàòîê îò äåëåíèÿ íà 4.
, ãäå mod 4 ýòî îñòàòîê îò äåëåíèÿ íà 4.
×èñëî  îêàçûâàåòñÿ âåùåñòâåííûì ÷èñëîì:
îêàçûâàåòñÿ âåùåñòâåííûì ÷èñëîì:

Êîðíè èç ìíèìîé åäèíèöû .
 ïîëå êîìïëåêñíûõ ÷èñåë êîðåíü n-îé ñòåïåíè èìååò n ðåøåíèé. Íà êîìïëåêñíîé ïëîñêîñòè êîðíè èç ìíèìîé åäèíèöû ðàñïîëîæåíû â âåðøèíàõ ïðàâèëüíîãî n-óãîëüíèêà, êîòîðûé âïèñàí â îêðóæíîñòü åäèíè÷íîãî ðàäèóñà.

Ýòî ñëåäóåò èç ôîðìóëû Ìóàâðà è òîãî, ÷òî ìíèìóþ åäèíèöó ìîæíî ïðåäñòàâèòü â òðèãîíîìåòðè÷åñêîì âèäå:

 ÷àñòíîñòè,  è
è 
Êðîìå òîãî, êîðíè èç ìíèìîé åäèíèöû ìîæíî ïðåäñòàâèòü â ïîêàçàòåëüíîì âèäå:


Êîðíè êâàäðàòíûå èç ìíèìîé åäèíèöû.

Êîðíè êóáè÷åñêèå èç ìíèìîé åäèíèöû (âåðøèíû òðåóãîëüíèêà).
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó àëãåáðû äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
×èñëà. Êîìïëåêñíûå (ìíèìûå) ÷èñëà. | |
| Êîìïëåêñíûå ÷èñëà (ìíèìûå ÷èñëà) ÷èñëà, êîòîðûå èìåþò âèä: x + iy , ãäå x è y âåùåñòâåííûå ÷èñëà, i ìíèìàÿ åäèíèöà (âåëè÷èíà, äëÿ êîòîðîé âûïîëíÿåòñÿ ðàâåíñòâî: i 2 = -1 ). | |
| ×èñëà. Êîìïëåêñíûå (ìíèìûå) ÷èñëà. | |
Ранее мы с вами разобрали пару крайне важных, в нашем мире, чисел: число Эйлера и число ПИ. Сегодня мы с вами узнаем еще об одном интересном и важном числе.
Мнимая единица, по сути, его нельзя назвать числом в привычном нам понимании. Это число не вещественное, а комплексное. Давайте пойдем по порядку.
Сперва история
Первые заметки о нем были обнаружены в записях Джероламо Кардано — итальянский математик живший в 16 веке. Он ввел его, когда решал кубические уравнения. Позже, когда ученые обнаружили эти записи, они начали производить с ним различные действия.
Основной вклад в развитие этой теории вложил ранее знакомый нам Леонард Эйлер. Тогда родился комплексный анализ, а позже и теория функций комплексного переменного (ТФКП). Леонард распространил основные функции в комплексную плоскость. Было сформулировано множество принципов, алгебраические действия не отличались от привычного вещественного анализа, но было сделано одно существенное допущение: в этой теории есть число, квадрат которого равен отрицательному числу. И это мнимая единица. Обозначается она как i, и такое название она получила благодаря все тому же Эйлеру (в некоторых других науках, таких как электротехника, встречается обозначение j, так как буква i занята для обозначения тока).
По определению мнимая единица — это число, квадрат которого равен -1 (i^2 = -1). Давайте попробуем поразмыслить, что это значит.
Для нахождения площади квадрата, мы возводим длину стороны этого квадрата в квадрат. То есть, мнимая единица — это сторона квадрата, у которого отрицательная площадь. Да, на реальности мы такого не встретим, именно по этому она называется мнимой. Но какой от нее тогда толк? Об этом немного позже.
Немного введу в курс дела
В комплексном анализе числовая прямая расширяется до комплексной плоскости, где осью абсцисс представлена вещественная прямая, а осью ординат — мнимая. Существует несколько способов записи комплексного числа: в виде пары чисел, в алгебраической форме, тригонометрической и вытекающей отсюда показательной.
Все формы представления в порядке, написанном выше
Самая красивая формула математики
Я хочу показать вам одну красивую формулу в математике, а для этого необходимо немного разобраться в комплексном анализе.
Давайте взглянем на комплексную плоскость поподробнее. На ней числа отмечаются точками, и каждой соответствует своя координата.
Но так же возможно векторное представление, где начало вектора лежит в начале координат, а конец на точке.
Благодаря этому возможно ввести показательное представление. Где число перед экспонентой показывает длину вектора, а угол в показателе равен углу между вещественной осью и этим вектором.
А теперь давайте рассмотрим следующий случай: пусть длина вектора равняется 1, а угол будет равен пи, то есть, пол оборота. Так мы попадем в точку -1 на вещественной оси.
То есть e^(i*pi) = -1. Переписав ее в несколько другом виде можно получить следующее выражение:
Это так называемая формула Эйлера (на самом деле это лишь частный случай этой формулы). И вся ее красота состоит в том, что она содержит в себе все знаменитые константы и числа.
Важность этого числа
Комплексный анализ очень важен для нашей жизни. В физике с его помощью описывают все волновые процессы. Вообще, говорят, что все волны и поля существуют в комплексном пространстве, а то, что мы видим, только тень «истинных» процессов. Квантовая механика, где и атом и другие материальные объекты — волны, делает такую трактовку более убедительной.
Так же, современная аэродинамика не обходится без ТФКП, где функции Жуковского могут давать необходимые профили крыла.
И это еще не все. Во многих отраслях так или иначе могут присутствовать элементы этой теории, поэтому ее важность нельзя отрицать.
Если данная статья была вам интересна, то не забывайте ставить пальцы вверх, я постарался написать для вас наиболее понятно. Так же подписывайтесь на канал, если еще не сделали этого! До скорых встреч и всего доброго! 🙂
Источник: https://www.equitieslab.com/wp-content/uploads/2017/04/816dfd710806e20aa40a7cd8c76d2e2d-e1557431746385.jp
Все из нас учились в школе и изучали математику, для кого-то это был скучный предмет и на уроках вы пускали бумажные самолетики, а для кого-то математика занимала не последнее место в списке любимых школьных предметов.
Каждый новый учебный год, изучение математики начинается с повторения пройденного материала и часто оно начиналось с разговора о числах. В с 1 по 4 класс вы знакомились с натуральными числами это: 1, 2, 3, 4, … (нужны при счёт (нумерации) предметов), потом познакомились с целыми числами (здесь грамотнее сказать «со множеством целых чисел»; оно обозначается буквой Z), это числа: -4,-3,-2,-1,0,1,2,3, … и т. д. в обе стороны, здесь нужно заметить, что множество целых чисел содержит в себе как натуральные числа (N), нуль и отрицательные числа, они появляются когда у нас нехватка чего-либо или у нас убыток чего-нибудь, например минус 120 рублей на счете мобильного телефона.
В средних классах вас уже знакомят с понятием дроби и определяют понятие рациональных и иррациональных чисел, где рациональные (обозначение Q) это числа, которые можно представить в виде обыкновенной дроби вида m/n, где m это целая число (называется числителем), а n натуральное число (называется знаменателем), например: 1/3, 2/3, 6/2, эти числа появляются, когда мы делим целый объект на части и берём их некоторое количество и тогда мы говорим, что взяли некоторое количество долей от общего. Иррациональные (от лат. irratio «несоотносимый»), числа ( I ), это такие числа, которые нельзя представить в виде обыкновенной дроби, например √2, для него можно указать только примерное значение (в виде десятичной дроби), т. е. √2≈1,4 (кстати, если вы хотите научиться вычислять квадратный корень любого числа, то в конце статьи вы можете найти все необходимые ссылки.) Немного погодя вас знакомят с заключительным множеством чисел, называемый множеством действительных (или вещественных) (обозначается как R от лат. realis «реальный, вещественный») чисел, оно объединяет все предыдущие множества чисел: натуральных, целых, рациональных и иррациональных. Математически можно записать получение множества вещественных чисел из других так: R ={N, Z, Q, I}, здесь фигурные скобки обозначают множества, а то, что внутри них называется элементами множества, но т. к. во множестве рациональных чисел уже содержаться и натуральные, и целые числа, то предыдущая запись эквивалентна такой: R={Q, I}.
После этого у вас должна сложится следующая картина в иерархии числовых множеств
Иерархия чисел. Источник: https://upload.wikimedia.org/wikipedia/commons/thumb/4/48/Diagramma_di_Venn_dei_numeri-ru.svg/1200px-Diagramma_di_Venn_dei_numeri-ru.svg.png
До зеленой области (на рисунке) всё понятно, но что можно сказать на счёт синей области, в которую входят все остальные множества. Эта область и называется, интересным названием— множеством комплЕксных чисел, здесь буква «е» сделана заглавной для того, чтобы можно было отличить обычное произношение слова от слова которое употребляют математики. Понятно, что кто-то мог только в первый раз услышать это слово, некоторые уже знакомы с ним, но многие могут задать вопрос: «Как эти числа появились и зачем нужны они, ведь уже и так достаточно по на придумывали разных чисел, не хватает что ли?» Разберемся по порядку. Для начала ответим на первую часть вопроса: «Как появились эти числа?» Что бы ответить на этот вопрос нужно разобрать одно интересное, но, на первый взгляд, простое уравнение:
x²+1=0,
найдем корни
x²= -1,
здесь уже могут некоторые удивится, как может квадрат числа быть отрицательным? Да, такие решения уравнений могут встречаться и они не редкость. Вот корни уравнения:
x[1, 2]=±√(-1).
Математика здесь подошла уже не к таким уж очевидным вещам, но я хочу сделать замечание для тех кто говорит, что такие абстракции это бред больной фантазии математиков. Чтобы понять причину появления нового множества чисел нужно разбираться в истории математики, здесь только скажем, что введение этих чисел было обусловлено возможностью решать уравнения, пример которых был показан выше и другие причины.
Следующая часть вопроса, «где они применяются?» Электротехника —например. Для расчета цепей переменного тока поголовно используются комплексные числа. Это очень удобно, представлять реактивные токи по мнимой оси, а активные по действительной (слова трудно понимаемые, но и понимать нам их сейчас не надо). Расчеты сводятся по сути к сложению, умножению, вычитанию и делению комплексных чисел. А без них пришлось бы решать интегрально-дифференциальные уравнения, что во много раз сложнее. А это тоже трудная задача. Если ещё нужен пример, то вот например, в квантовой механике тоже используются комплексные числа, для вычисления волновой функции, которая выглядит вот так:
волновая (пси-)функция
Теперь разберемся с определением и видом комплексных чисел:
Определение.
Ко́мпле́ксные числа — числа вида a+bi , где a и b— вещественные числа, i— мнимая единица , то есть число, для которого выполняется равенство:
i²=–1 (ничего не напоминает?.. Да это квадрат нашего x -са, уравнения— x²+1=0).
Мни́мая едини́ца — комплексное число, квадрат которого равен −1 (минус единице), то есть i²=—1.
Вообще общий вид комплексного числа такой: z=a+bi, где число a называется действительной частью, а число b его мнимой частью, также встречается трактовка того, что мнимой частью называют произведение b и мнимой единицы i.
Далее разберемся с тем, какие арифметические действия можно производить над комплексными числами.
Вообще говоря, действия над комплексными числами определены так, чтобы над операциями выполнялись все три основных свойства :
- Коммутативность(переместительное свойство)— это когда a+b=b+a;
- Ассоциативность(сочетательное свойство)— это когда a+(b+c)=c+(a+b);
- Дистрибутивность (распределительное свойство)— это когда a(b+c)=ab+ac.
Ну например:
2+3i=a, 5+5i=b; Найти — a+b=? Решение:
2+3i+5+5i=7+8i. И так со всеми любыми другими операциями: умножением, делением, вычитанием, возведением в степень…
Умножение проходит как и при обычном произведении сумм чисел, например, найти произведение чисел: a=2+4i и b=1-2i. Получим, a•b=(3+5i)(1-2i)=3•1-6i+5i+10=13-i. Хочу заметить, что, когда мы находили произведение 5i на (-2i), то перемножая их мы получим квадрат i, а он как мы знаем равен (-1) и поэтому произведение равно 10.
С делением немного сложнее. Для начала нужно ввести новое понятие, а именно сопряженное комплексное число данному комплексному числу. Оно определяется просто…
Сопряженным числом z’ числу z=a+bi называется такое число, что z’=a-bi.
То есть в сопряженном числе знак между действительной и мнимой частями всегда противоположен знаку того числа, с которым он сопряжен. Можно даже так запоминать знак сопряженного числа: если z=a±bi, то z’=a∓bi.
Теперь можно поговорить о том как делить комплексные числа.
Если у нас есть два комплексных числа одно из которых мы делим на другое, то нам нужно числитель и знаменатель дроби домножить на число сопряженное знаменателю. Затем произвести перемножение в числителе и знаменателе и при возможности упростить полученные выражения.
Например, разделить a=3-i на b=7+2i.
a/b=(3-i)/(7+2i)=((3-i)•(7-2i))/((7+2i)•(7-2i))=(19-13i)/53=(19/53)-13i/53.
Можете попробовать сами решить вот такой пример: (9+i)/(3-2i).
Ответ: 25/13+21i/13.
Комплексные числа в математике также как и обычные числа могут быть изображены графически, мы помни как в школе мы рисовали числовую ось и на ней обозначали числа, это выглядело как-то так:
Числовая ось. Источник: https://www.smp.org.py/images/eventos/recta.jpg
Но комплексные числа на то и комплексные (от лат. complex «сложный»), потому что состоят из двух частей: действительной и мнимой, поэтому представление комплексных чисел нуждалось в модификации числовой оси, конкретно — требовалось добавить ось, которая была бы перпендикулярна нашей изначальной оси (теперь, называемой действительной; обозначение Re), назвав её мнимой (обозначение Im от лат. imaginarium «воображенный, выдуманный»), а саму систему изображения чисел — комплексной плоскостью. Выглядит она так:
Комплексная плоскость. Источник: https://i.imgur.com/WCasQl7.png
По рисунку видно, что таким образом комплексное число задается с помощью значений «икса (x)» и «игрека (y)», которые задают наше комплексное число z. Кстати, с помощью графического способа представления чисел можно показать сопряженные числа вот так
Сопряженные комплексные числа. Источник: https://upload.wikimedia.org/wikipedia/commons/thumb/7/7c/Complex_conjugate_picture-01.svg/220px-Complex_conjugate_picture-01.svg.png
На рисунке сопряженное комплексное число число обозначено буквой z с чертой над ней.
Да, и ещё одна форма представления чисел — тригонометрическая, она как раз представлена на этом рисунке. Чтобы описать комплексное число тригонометрически нам нужно модифицировать комплексную плоскость, а именно нужно выбрать одну из осей в качестве направления отсчета угла поворота (далее скажем чего). Далее нужно выбрать точку отсчета (или начало отсчета) оставим точку центра системы координат (— точка их пересечения) и от неё отложить так называемый полярный радиус (в физике ему дано иное название и вы его возможно слышали — это радиус-вектор). Тогда на плоскости комплексное число можно задать, т. е. описать точку, которая это число обозначает, как угол поворота этого полярного радиуса и его длины от начала отсчета до этой точки (см. предыдущий рисунок). Из такого представления (описания) можно выразить привычные нам абсциссу (действительную часть) комплексного числа и ординату (мнимую часть) комплексного числа через определения синуса и косинуса, т. е. его абсцисса x равна: x=rcos(ϕ), а ордината y=rsin(ϕ). Тогда комплексное число равно: z=x+yi=rcos(ϕ)+risin(ϕ)=r(cos(ϕ)+isin(ϕ)). С помощью тригонометрической записи комплексных чисел можно записать одно из важнейших соотношений, называется оно «Формулой Муавра»
Формула Муавра
Она показывает то, как возводить комплексные числа в натуральную степень. Её доказательство просто, здесь оно не приведено — его можно найти в Интернете.
Подводя итог, скажу, что помимо комплексных чисел были придуманы еще более фантастические числа, называемые гиперкомплексными, это: кватернионы, октонионы(O) и седенионы, но это уже слишком сложная тема, чтоб на пальца её рассказать.
Вот собственно это всё, что я хотел вам рассказать, так сказать вы, прочитав эту статью, получили базовые представления о комплексном исчислении. Удачи!
Ссылки:
— Извлечение квадратных корней столбиком;
— Гиперкомплексные числа;
— Реальность комплексных чисел;
— Подписывайтесь на наш канал и вступайте в группу во ВКонтакте.
Единица — вздор! Единица — ноль!
~ Маяковский про мнимую единицу
Мнимая единица (讠, один с точечкой) — это:
- … мнимое число, которое определяется так: мнимая единица, умноженная на мнимую единицу, умноженная на мнимую единицу ещё раз, и ещё умноженная два раза на мнимую единицу, умноженная на мнимую единицу равна −1. Если то, что говорится в предыдущем предложении истинно, то оно ложно, если ложно — то истинно.
- выше была приведёна упрощённая формулировка для двоечников. Крайне сложная формулировка такова: .
Эта вторая формулировка крайне сложна. Чтобы её понять и привести к простой, нужно разбить одно окно чем-нибудь, другое — головой. И сравнить осколки обоих стёкол и состояние головы и крыши до и после процедуры.
История открытия[править]
История мнимой единицы такова. Математик, напившись, сел за компьютер. Там он открыл блокнот, чтобы напечатать чистый лист из принтера и высморкаться в него. Но из-за пьянки он нечаянно нажал знак i. Шрифт был большим, потому что вчера он учил ребёнка примеру . Вот он и напечатал этот лист. И высморкался в него. Поэтому лист стал мятым. Он сказал: «Мятая единица с точечкой». А его друг не расслышал и сказал: «Мнимая единица… Эээ… Эх, какая водочка! Козявочкин, к доске! Вот тебе, двоечник, ещё пример. Вот это число в квадрате равно…». А наш математик ответил: «О, да, давай ещё стопочку! Ааа… Ты что, не знаешь отрицательных чисел? Нужно слушать, что говорят на уроке. Ответ равен минус одному». И они стали продолжать пить. Открытие осталось бы незапомненным, если бы не вор, который пробрался украсть компьютер. Он нёс с собой диктофон. И записывал всё, что говорили пьяные учёные. Зачем — неизвестно. Вор украл компьютер. Он хотел включить его, подключив к молниеотводу один провод, а другой — засунув себе в рот. Ударила молния… Дальше понятно. А диктофон нашёл пьяница и бросил его в окно дома учёных с целью разбить его. Он добился своего, но в то же время оказал невообразимое содействие науке. Учёные-математики после отрезвления прочитали запись в диктофоне и поняли, что они совершили открытие! Записав, что они сказали тогда, в математической форме, они получили выражение:
Но оно было очень сложное, и понять его не удалось даже этим двум математикам. Математик, который напечатал мнимую единицу и высморкался в лист, поблагодарил своего друга за исправление. Вскоре, проанализировав осколки разбитого окна, математики решили, что данных для того, чтобы понять их слова, недостаточно. Поэтому они стали думать. Но вдруг один из них понял, что надо делать. И разбил головой другое окно. Сделав записи состояний окон, головы и крыши, он, проведя сложнейшие расчёты, решил, что крыша у него съехала и что мнимая единица, умноженная на мнимую единицу, умноженная на мнимую единицу ещё раз, и ещё умноженная два раза на мнимую единицу, умноженная на мнимую единицу равна .
Основные свойства[править]
После того, как сбрендившие учёные поняли, что такое мнимая единица, стали выводить разные формулы. Например:
, поэтому , далее: ,
В итоге доказано, что , т.е отрицательные и положительные числа неотличимы.
Теперь докажем одно из самых важных свойств мнимой единицы — то, что в любом выражении её можно заменить на . Точку можно поставить и справа, содержание от этого не изменится. Действительно, ведь мнимая единица — это единица с точечкой, то есть со знаком умножения, что и требовалось доказать.
Далее:
В итоге мы получили e-нное представление числа — это
Тождество Эйлера[править]
Существует следующее тождество:
Его высказал Эйлер, один из трезвых учёных, во сне. Поэтому его называют тождеством Эйлера. До сих пор учёные всего мира не понимают смысл этой формулы и удивляются её странностью. Не меньше удивления вызывает то, что этот великий математик подарил открытие миру в спящем состоянии. Он, проснувшись, показывал, что ничего не помнит, что ему «опять снились эти формулы бессмысленные». Но никто и не подумал пренебрегать великим открытием. Все без исключения должны верить тому, что сказал Эйлер, поскольку он уже сделал много великих открытий. Он просто не захотел раскрывать строгого доказательства. Известны несколько доказательств, но известны и их опровержения.
Доказательство[править]
Т.к , данную формулу можно переписать в виде: . Первую формулу также перепишем: . Перемножим эти формулы:
В итоге мы получили верное равенство, которое вытекает из исходного, поэтому тождество Эйлера доказано!
Опровержение[править]
Т.к мнимая единица — это 1 с точечкой, или проще говоря, . Поэтому:
Тождество опровергнуто.
Опровержение опровержения[править]
Не верьте этому опровержению, Эйлер говорил правду!!! (остальные 54 308 428 790 203 478 762 340 052 723 346 983 453 487 023 489 987 231 275 412 390 872 348 472 восклицательных знака были удалены автоматическим фильтром)
Следствие 1[править]
Из тождества Эйлера следует нечто совсем уж парадоксальное. Перепишем тождество Эйлера в таком виде:
Поскольку в правой части равенства стоит действительное число, значит и в левой части тоже действительное число. В таком случае мы можем смело возвести обе части этого равенства в квадрат:
Отсюда неминуемо следует, что , а значит, . Говорят, когда Эйлер это обнаружил, он свернулся в ленту Мёбиуса и укатился в Соловецкий монастырь, где и закончил свои дни в полном безумии. Тем не менее, официальная наука доказала, что Эйлер заразился безумием от Фридриха Ницше, к тому времени ещё бывшего одним из носителей бесов безумия.
Следствие 2[править]
Еще раз рассмотрим вышеприведённое тождество Эйлера:
А теперь возведем обе его части в любую целую нечётную степень n:
А значит, при любом нечётном n,
. Логарифмируя по основанию е, получаем
Сокращая на , получаем n=1, то есть каждое нечётное целое число равно единице.
Отсюда со всей очевидностью следует божественность мироздания, множественность параллельных миров и реальность существования чебурашек в дикой природе.
Интересные факты[править]
- Если пользоваться мнимой единицей, то существует вероятность 65 % сдать ЕГЭ по математике на 95 баллов путем выноса мозга проверяющим.
- Вполне возможно, что успех компании Apple принесла именно мнимая единица, подсознательно влияющая на моск и вызывающая мнимое представление о реальных вещах.
- Поделить мнимую единицу на ноль можно: получается Мнимая бесконечность.
- Кроме мнимой единицы существуют и мнимая двойка, тройка, четверка и т. д. Однако ими не пользуются, ибо нефиг!
- Британские ученые доказали, что если выйти в плоскость комплексных чисел, то по замкнутому контуру можно проходить сквозь двери. Однако всех, кто пытался доказать это на практике, засосало в нуль-телепорт.
- Исходя из вышеописаного явления, можно предположить, что черная дыра может существовать только в плоскости комплексных чисел.
- Существует мнение, что изображение мнимой единицы получилось путем банального переворачивания знака !. Возможно это сделали для того, чтобы показать, насколько это число опасно и таинственно, и лучше глубоко не лезть в эти дебри. Скорее всего так и есть: в последнее время почти никто не занимается изучением мнимой единицы, особенно после экспериментов британских ученых. И только безумные ученые изредка решаются рискнуть своими задницами ради очередного, никому не нужного, мнимого открытия.
Человекам далеко не сведущим в математике, физике и алгебре, да что уж там — геометрии, рассуждения о мнимой единице представляется полным бредом. Прежде чем о ней рассуждать необходимо определиться, что такое отрицательные числа в природе. Дак, вот их НЕТ. Также как не может быть отрицательной скорости. Отрицательные числа прибывают в нашем воображении из-за того, что мы принимаем какое-либо значение за НОЛЬ. К примеру
рассмотрим температуру вещества, а именно абсолютный ноль по Цельсию, это −273,15 °C (-459,67° по Фаренгейту), то есть полный покой вещества, когда его атомы «обездвижены» — вот это и есть НОЛЬ. Отсюда следует отрицательные числа, которые кажутся таковыми, следует записывать в скобках, например так:(-1). Физический смысл отрицательной степени — отсутствует.
далее
в нормальном виде
приведем в нормальный вид , раскроем скобки и получим , именно так должна выглядеть формула,МЫ ЖЕ ЗНАЕМ со школы «При перемножении одного положительного и одного отрицательного числа результат всегда будет отрицательным числом!»(кстати, никто не может объяснить этого правила в физическом смысле!) отсюда следует вывод в физическом смысле ВСЕ ОТРИЦАТЕЛЬНЫЕ ЧИСЛА = 0 Их не существует!
В итоге Эйлером доказано, что 1=-1, такой же единице только по другую сторону шкалы!!!
