Какое из свойств магнитного поля выражает теорема гаусса
Анонимный вопрос · 27 января 2019
1,0 K
Имею естественно научное образование, в юношестве прикипел к литературе, сейчас…
Это теорема для магнитной индукции, звучит так:
> поток вектора магнитной индукции через любую замкнутую поверхность равен нулю
В виде формулы выглядит так Читать далее
Кто изобрел пушку Гаусса?
Информация из Википедии
Пушка Гаусса (англ.Gauss gun, Coil gun, Gauss cannon) — одна из разновидностей электромагнитного ускорителя масс. Названа по имени немецкого учёного Карла Гаусса, заложившего основы математической теории электромагнетизма. Следует иметь в виду, что этот метод ускорения масс используется в основном в любительских установках, так как не является достаточно эффективным для практической реализации. По своему принципу работы (создание бегущего магнитного поля) сходна с устройством, известным как линейный двигатель.
А теперь проще
Сама пушка представляет из себя трубку-ствол обмотанную ч/л пропускающим ток, создается магнитное поле, соответственно железо помещенное в ствол стремится к середине установки
После прохождения через центр, соответственно, начинает притягиваться обратно но при правильной сборке снаряд (чаще всего намагниченный, дабы невилировать данный эффект) быстро проходит через центр и выходит из ствола
Нет ли такой теории, что Земля и Луна — это два магнита разной полярности?
Заходим и слушаем: https://soundcloud.com/soulbringer-1
Если вы имеет ввиду то что луна вращается вокруг земли по принципу отталкивающихся магнитов, то такой официальной теории нет. Но не удивлюсь, если какие-то фрики придумают такую теорию, а потом её покажут по телеканалу РЕН-ТВ. А если вы спрашиваете про магнитные поля, то они у земли и у луны есть. Например на земле вы можете наблюдать их эффект посмотрев на компас. На луне тоже есть небольшие магнитные поля.
Прочитать ещё 1 ответ
Кто первый из учёных доказал, что вокруг проводника с током существует магнитное поле?
Опыт Эрстеда заключается в следующем. На столе располагают магнитную стрелку, которая ориентируется с севера на юг в магнитном поле Земли, и параллельно ей сверху проводник, соединённый с источником тока. При замыкании цепи стрелка повернётся на 90° и встанет перпендикулярно проводнику. При размыкании цепи стрелка вернётся в первоначальное положение. Если изменить направление тока на противоположное, то стрелка повернётся в обратную сторону. Опыт Эрстеда доказывает, что вокруг проводника, по которому течёт электрический ток, существует магнитное поле, которое действует на магнитную стрелку.
Объясните теорему Гёделя о неполноте простым языком для нематематика пожалуйста. Постулаты, практическое значение, влияние на философию?
Не хотелось мне отвечать на этот вопрос, но судя по тому какую херню тут пишут — все же придется.
Во-первых Теорема Геделя — это Теорема о свойствах конкретной формальной системы — арифметике Пеано (один из способов аксиоматического описания натуральных чисел). Теорема утверждает о том, что в арифметике Пеано существует формула, которую нельзя ни доказать ни опровергнуть средствами самой арифметики.
Вот собственно и все, особого практического значения здесь нет никакого. Однако философское осмысление теоремы разные люди начали переиначивать на свой лад. Некоторые кибернетики говорили, что она утверждает невозможность искусственного интеллекта как такового. Физиологи говорили, например, о тщетности опытов с собаками Павлова, от которых требовалось детерминированное поведение. Физики говорили о невозможности описания сложных физических объектов (черных дыр и проч.). Про что говорили журналисты, я вообще молчу. И меньше всего интерпретацией занимались, наверно, сами математики.
Все эти утверждения возможно и верны, но они не имеют никакого отношения к теореме Геделя. Потому что теорема Геделя утверждает только о свойствах арифметики Пеано. И даже факт того, что какие-то формулировки не могут быть доказаны самой системой — не является смертельным, так как 1) они могут быть неинтересны в практическом смысле, 2) могут быть доказаны в рамках другой формальной системы.
Прочитать ещё 1 ответ
Для полноценного описания электростатического поля заданной системы зарядов в вакууме достаточно экспериментально подтвержденного закона Кулона и принципа суперпозиции. Но при этом существует возможность свойства электростатического поля охарактеризовать в ином обобщенном виде, не опираясь на утверждения касательно кулоновского поля точечного заряда.
Поток вектора напряженности
Зададим новую физическую величину, описывающую электрическое поле – поток Φ вектора напряженности электрического поля. Предположим, что в пространстве, содержащем заданное электрическое поле, имеется некая достаточно малая площадка ΔS.
Определение 1
Элементарный поток вектора напряженности (через площадку S) – это физическая величина, равная произведению модуля вектора E→, площади ΔS и косинуса угла α между вектором и нормалью к площадке:
ΔΦ=EΔScos α=EnΔS.
В данной формуле En является модулем нормальной составляющей поля E→.
Рисунок 1.3.1. Иллюстрация элементарного потока ΔΦ.
Пример 1
Теперь возьмем для рассмотрения некую произвольную замкнутую поверхность S. Разобьем заданную поверхность на площадки небольшого размера ΔSi, рассчитаем элементарные потоки ΔΦi поля через эти малые площадки, после чего найдем их сумму, что в итоге даст нам поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):
Φ=∑∆Φi=∑Em∆Si
Когда речь идет о поверхности замкнутого типа, всегда используется внешняя нормаль.
Рисунок 1.3.2. Расчет потока Ф через произвольную замкнутую поверхность S.
Теорема Гаусса. Доказательство
Теорема или закон Гаусса для электростатического поля в вакууме является одним из основных электродинамических законов.
Теорема 1
Поток вектора напряженности электростатического поля E→ через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε0.
Уравнение Гаусса имеет вид:
Φ=1ε0∑qвнутр
Доказательство 1
Докажем указанную теорию: для этого исследуем сферическую поверхность (или поверхность шара) S. В центре заданной поверхности расположен точечный заряд q. Любая точка сферы обладает электрическим полем, перпендикулярным поверхности сферы и равным по модулю:
E=En=14πε0·qR2,
где R является радиусом сферы.
Поток Φ через поверхность шара запишется, как произведение E и площади сферы 4πR2. Тогда: Φ=1ε0q.
Следующим нашим шагом будет окружение точечного заряда произвольной поверхностью S замкнутого типа; зададим также вспомогательную сферу R0(рис. 1.3.3).
Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд.
Возьмем для рассмотрения конус с малым телесным углом ΔΩ при вершине. Рассматриваемый конус задаст на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки являются одинаковыми. В самом деле:
ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS’,
где выражением ΔS’=ΔS cos α определяется площадка, которая задастся конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Поскольку ∆S0∆S’=R02r2, то ∆Φ0=∆Φ. Из полученного следует вывод о том, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
Φ=Φ0=qε0.
Так же мы можем продемонстрировать, что, когда замкнутая поверхность S не охватывает точечный заряд q, поток Φ равен нулю. Этот случай проиллюстрирован на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, т.е. в этой области не наблюдается обрыва или зарождения силовых линий.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов является следствием из принципа суперпозиции. Поле любого распределения зарядов возможно записать в виде векторной суммы электрических полей точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S сложится из потоков Φi электрических полей отдельных зарядов. Когда заряд qiрасположен внутри поверхности S, он дает вклад в поток, равный qiε0. В случае расположения заряда снаружи поверхности его вклад в поток есть нуль.
Так, мы доказали теорему Гаусса.
Замечание 1
Теорема Гаусса, по сути, есть следствие закона Кулона и принципа суперпозиции. Однако, взяв за изначальную аксиому утверждения теоремы, следствием станет закон Кулона, в связи с чем теорему Гаусса порой называют альтернативной формулировкой закона Кулона.
Опираясь на теорему Гаусса, в определенных случаях легко определить напряженность электрического поля вокруг заряженного тела (при наличии заранее угаданных симметрии заданного распределения зарядов и общей структуры поля).
Применение теоремы Гаусса
Пример 2
В качестве примера можно рассмотреть задачу, в которой необходимо вычислить поле тонкостенного полого однородно заряженного длинного цилиндра с радиусом R. Такая задача имеет осевую симметрию, и из соображений симметрии электрическое поле должно иметь направление по радиусу. Таким образом, чтобы иметь возможность применить теорему Гаусса, оптимально выбрать поверхность замкнутого типа S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
Рисунок 1.3.4. Иллюстрация поля однородно заряженного цилиндра. OO’ – ось симметрии.
Если r≥R, то весь поток вектора напряженности пройдет через боковую поверхность цилиндра, поскольку поток через оба основания есть нуль. Формула площади боковой поверхности цилиндра запишется как: 2πrl. Применим закон Гаусса и получим:
Φ=E2πrl=τlε0.
В указанном выражении τ является зарядом длины цилиндра. Далее можно записать:
E=τ2πε0r.
Данное выражение не имеет зависимости от радиуса R заряженного цилиндра, а значит оно применимо и к полю длинной однородно заряженной нити.
Чтобы найти напряженность поля внутри заряженного цилиндра, необходимо создать замкнутую поверхность для случая r<R. В соответствии с симметрией задачи поток вектора напряженности через боковую поверхность цилиндра должен быть, и в этом случае он равен Φ=E2πrl. Исходя из гауссовской теоремы, этот поток находится в пропорции к заряду, расположенному внутри замкнутой поверхности. Заряд этот равен нулю, откуда вытекает, что электрическое поле внутри однородно заряженного длинного полого цилиндра тоже есть нуль.
Точно так же теорема и формула Гаусса применимы для определения электрического поля в иных случаях, когда распределение зарядов охарактеризовано какой-либо симметрией, к примеру, симметрией относительно центра, плоскости или оси. Во всех этих случаях необходимо выбирать замкнутую гауссову поверхность подходящей формы.
Пример 3
К примеру, в случае центральной симметрии поверхность оптимально выбрать в виде сферы, у которой центр расположен в точке симметрии. Когда мы имеем симметрию относительно оси, подходящим видом замкнутой поверхности будет соосный цилиндр, закрытый с обоих торцов (аналогично рассмотренному выше примеру).
При отсутствии симметрии и невозможности угадать общую структуру поля, теорема Гаусса не сможет быть применена для упрощения решения задачи по определению напряженности поля.
Пример 4
Разберем еще пример распределения зарядов при наличии симметрии: нахождение поля равномерно заряженной плоскости (рис. 1.3.5).
Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность.
Здесь гауссову поверхность S оптимально задать как цилиндр некой длины, замкнутый с обоих концов. Ось цилиндра является перпендикуляром к заряженной плоскости; в свою очередь, торцы цилиндра находятся на одинаковом расстоянии от нее. В соответствии с симметрией поле равномерно заряженной плоскости должно везде иметь направление по нормали. Применим теорему Гаусса и получим:
2E∆S=σ∆Sε0 или E=σ2ε0.
Здесь σ является поверхностной плотностью заряда или зарядом, приходящимся на единицу площади.
Выражение, которое мы получили для электрического поля однородно заряженной плоскости, возможно использовать и для плоских заряженных площадок конечного размера: здесь расстояние от точки, в которой мы определяем напряженность поля, до заряженной площадки должно быть значимо меньше размеров площадки.
Экспериментально установленные закон Кулона и принцип суперпозиции позволяют полностью описать электростатическое поле заданной системы зарядов в вакууме. Однако, свойства электростатического поля можно выразить в другой, более общей форме, не прибегая к представлению о кулоновском поле точечного заряда.
Введем новую физическую величину, характеризующую электрическое поле – поток Φ вектора напряженности электрического поля. Пусть в пространстве, где создано электрическое поле, расположена некоторая достаточно малая площадка ΔS. Произведение модуля вектора на площадь ΔS и на косинус угла α между вектором 
и нормалью 
к площадке называется элементарным потоком вектора напряженности через площадку ΔS (рис. 1.3.1):
где En – модуль нормальной составляющей поля
 |
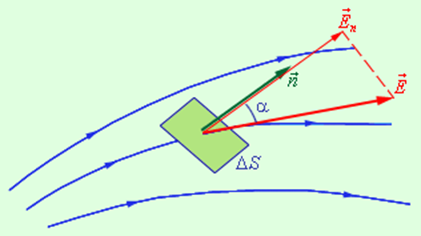| Рисунок 1.3.1. К определению элементарного потока ΔΦ |
Рассмотрим теперь некоторую произвольную замкнутую поверхность S. Если разбить эту поверхность на малые площадки ΔSi, определить элементарные потоки ΔΦi поля через эти малые площадки, а затем их просуммировать, то в результате мы получим поток Φ вектора через замкнутую поверхность S (рис. 1.3.2):
В случае замкнутой поверхности всегда выбирается внешняя нормаль.
 |
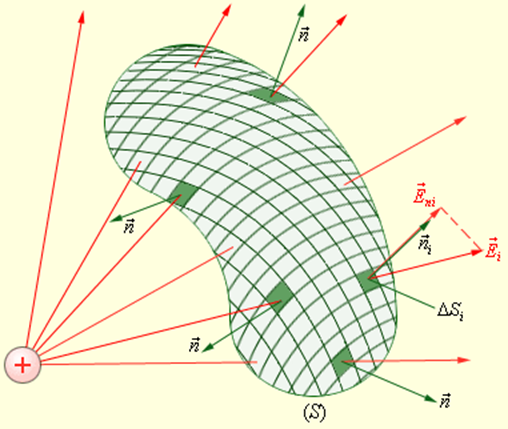| Рисунок 1.3.2. Вычисление потока Ф через произвольную замкнутую поверхность S |
Теорема Гаусса утверждает:
Поток вектора напряженности электростатического поля 
через произвольную замкнутую поверхность равен алгебраической сумме зарядов, расположенных внутри этой поверхности, деленной на электрическую постоянную ε.
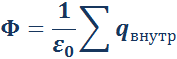
Для доказательства рассмотрим сначала сферическую поверхность S, в центре которой находится точечный заряд q. Электрическое поле в любой точке сферы перпендикулярно к ее поверхности и равно по модулю
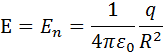
где R – радиус сферы. Поток Φ через сферическую поверхность будет равен произведению E на площадь сферы 4πR2. Следовательно, 
Окружим теперь точечный заряд произвольной замкнутой поверхностью S и рассмотрим вспомогательную сферу радиуса R0 (рис. 1.3.3).
 |
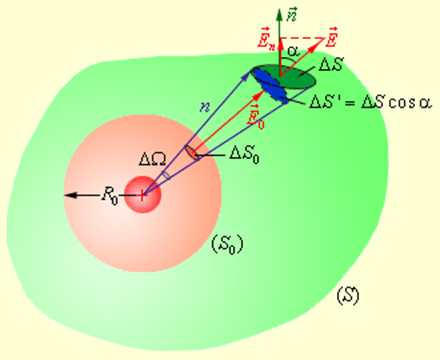| Рисунок 1.3.3. Поток электрического поля точечного заряда через произвольную поверхность S, окружающую заряд |
Рассмотрим конус с малым телесным углом ΔΩ при вершине. Этот конус выделит на сфере малую площадку ΔS0, а на поверхности S – площадку ΔS. Элементарные потоки ΔΦ0 и ΔΦ через эти площадки одинаковы. Действительно,
ΔΦ0 = E0ΔS0, ΔΦ = EΔS cos α = EΔS ‘.
Здесь ΔS’ = ΔS cos α – площадка, выделяемая конусом с телесным углом ΔΩ на поверхности сферы радиуса n.
Так как 
, a 
, следовательно 
Отсюда следует, что полный поток электрического поля точечного заряда через произвольную поверхность, охватывающую заряд, равен потоку Φ0 через поверхность вспомогательной сферы:
Аналогичным образом можно показать, что, если замкнутая поверхность S не охватывает точечного заряда q, то поток Φ = 0. Такой случай изображен на рис. 1.3.2. Все силовые линии электрического поля точечного заряда пронизывают замкнутую поверхность S насквозь. Внутри поверхности S зарядов нет, поэтому в этой области силовые линии не обрываются и не зарождаются.
Обобщение теоремы Гаусса на случай произвольного распределения зарядов вытекает из принципа суперпозиции. Поле любого распределения зарядов можно представить как векторную сумму электрических полей 
точечных зарядов. Поток Φ системы зарядов через произвольную замкнутую поверхность S будет складываться из потоков Φi электрических полей отдельных зарядов. Если заряд qi оказался внутри поверхности S, то он дает вклад в поток, равный 
если же этот заряд оказался снаружи поверхности, то вклад его электрического поля в поток будет равен нулю.
Таким образом, теорема Гаусса доказана.
Теорема Гаусса является следствием закона Кулона и принципа суперпозиции. Но если принять утверждение, содержащееся в этой теореме, за первоначальную аксиому, то ее следствием окажется закон Кулона. Поэтому теорему Гаусса иногда называют альтернативной формулировкой закона Кулона.
Используя теорему Гаусса, можно в ряде случаев легко вычислить напряженность электрического поля вокруг заряженного тела, если заданное распределение зарядов обладает какой-либо симметрией и общую структуру поля можно заранее угадать.
Примером может служить задача о вычислении поля тонкостенного полого однородно заряженного длинного цилиндра радиуса R. Эта задача имеет осевую симметрию. Из соображений симметрии электрическое поле должно быть направлено по радиусу. Поэтому для применения теоремы Гаусса целесообразно выбрать замкнутую поверхность S в виде соосного цилиндра некоторого радиуса r и длины l, закрытого с обоих торцов (рис. 1.3.4).
 |
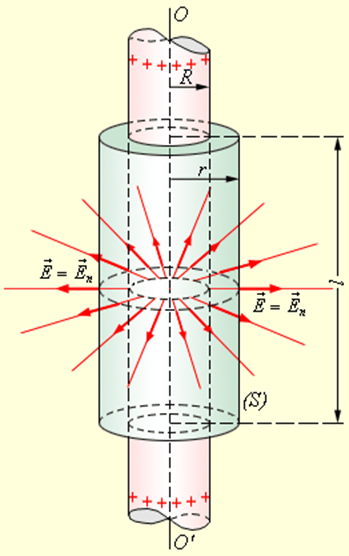| Рисунок 1.3.4. Вычисление поля однородно заряженного цилиндра. OO’ – ось симметрии |
При r ≥ R весь поток вектора напряженности будет проходить через боковую поверхность цилиндра, площадь которой равна 2πrl, так как поток через оба основания равен нулю. Применение теоремы Гаусса дает:
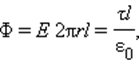
где τ – заряд единицы длины цилиндра. Отсюда
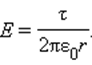
Этот результат не зависит от радиуса R заряженного цилиндра, поэтому он применим и к полю длинной однородно заряженной нити.
Для определения напряженности поля внутри заряженного цилиндра нужно построить замкнутую поверхность для случая r < R. В силу симметрии задачи поток вектора напряженности через боковую поверхность гауссова цилиндра должен быть и в этом случае равен Φ = E 2πrl. Согласно теореме Гаусса, этот поток пропорционален заряду, оказавшемуся внутри замкнутой поверхности. Этот заряд равен нулю. Отсюда следует, что электрическое поле внутри однородно заряженного длинного полого цилиндра равно нулю.
Аналогичным образом можно применить теорему Гаусса для определения электрического поля в ряде других случаев, когда распределение зарядов обладает какой-либо симметрией, например, симметрией относительно центра, плоскости или оси. В каждом из таких случаев нужно выбирать замкнутую гауссову поверхность целесообразной формы. Например, в случае центральной симметрии гауссову поверхность удобно выбирать в виде сферы с центром в точке симметрии. При осевой симметрии замкнутую поверхность нужно выбирать в виде соосного цилиндра, замкнутого с обоих торцов (как в рассмотренном выше примере). Если распределение зарядов не обладает какой-либо симметрией и общую структуру электрического поля угадать невозможно, применение теоремы Гаусса не может упростить задачу определения напряженности поля.
Рассмотрим еще один пример симметричного распределения зарядов – определение поля равномерно заряженной плоскости (рис. 1.3.5).
|
| Рисунок 1.3.5. Поле равномерно заряженной плоскости. σ – поверхностная плотность заряда. S – замкнутая гауссова поверхность |
В этом случае гауссову поверхность S целесообразно выбрать в виде цилиндра некоторой длины, закрытого с обоих торцов. Ось цилиндра направлена перпендикулярно заряженной плоскости, а его торцы расположены на одинаковом расстоянии от нее. В силу симметрии поле равномерно заряженной плоскости должно быть везде направлено по нормали. Применение теоремы Гаусса дает:
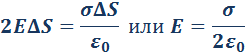
где σ – поверхностная плотность заряда, т. е. заряд, приходящийся на единицу площади.
Полученное выражение для электрического поля однородно заряженной плоскости применимо и в случае плоских заряженных площадок конечного размера. В этом случае расстояние от точки, в которой определяется напряженность поля, до заряженной площадки должно быть значительно меньше размеров площадки.