Какие бывают свойства фигур
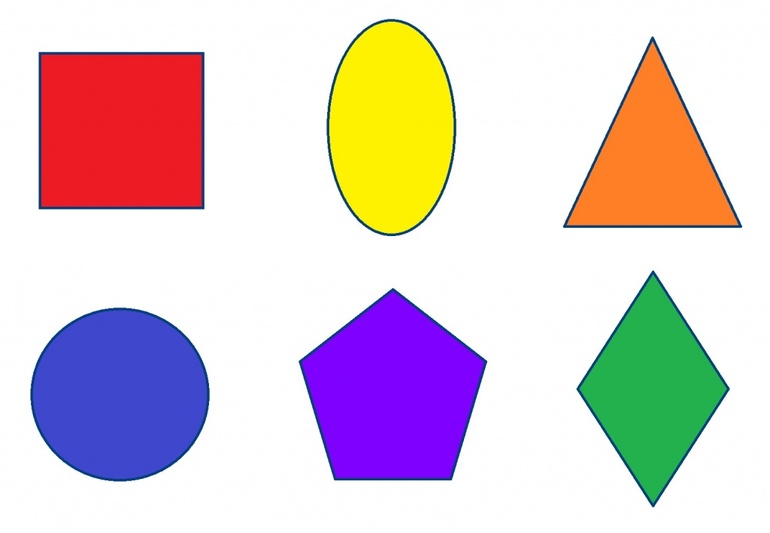
В статье дается определение, основные свойства и формулы для следующих геометрических фигур:
Четырехугольник (общее для всех четырехугольников)
Квадрат
Прямоугольник
Параллелограмм
Ромб
Трапеция
Треугольник
Окружность
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a2или S=d2/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2
где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)
где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1)2+(d2)2=(a2+b2)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
Площадь по двум сторонам и углу между ними: S=a*b*sin α
Площадь по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
где a, b — длины сторон, d1, d2 –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d1*d2)/2
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a2 · sin α
Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a
где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2
где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь по сторонам и углу между ними: S=(a*b)/2* sin γ
Площадь по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
Площадь по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d1, d2 –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
- Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
- Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
- В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
- Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Основные формулы:
Длина окружности: L = 2πR
Площадь круга: S = π*r2 или S = π*d2/4
где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.
Александр А. · 18 мая 2019
6,8 K
Копирайтер, увлекаюсь психологией и философией. Люблю искусство и моду
Фигуры на плоскости изучают раздел геометрии- планиметрия. Геометрическая фигура-это любое множество точек.
Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской. Например, отрезок, прямоугольник – это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида.
Основные свойства простых фигур выражаются в аксиомах:
- Какова бы ни была прямая, существуют точки, принадлежащие этой прямой и не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Эта аксиома выражает основное свойство принадлежности точек и прямых на плоскости.
- Из трех точек на прямой одна и только одна лежит между двумя другими.
Этой аксиомой выражается основное свойство расположения точек на прямой.
- Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Очевидно, что аксиома 3 выражает основное свойство измерения отрезков.
- Прямая разбивает плоскость на две полуплоскости.
Этим предложением выражается основное свойство расположения точек относительно прямой на плоскости.
Правда ли, что всю геометрию и тригонометрию можно доказать теоремой Пифагора? :D?
математик-системный программист, асу тп для аэс.
теорема пифагора действительно очень важна и очень часто используется в самых разных задачах, но база геометрии в другом, и сама теорема пифагора в школьном курсе также доказывается.
доказательство всегда базируется на системе аксиом, которые считаются непогрешимыми в рамках предметной области и не доказываются. и одной теоремы пифагора тут мало.
есть понятия, что такое точка,прямая, длинна, площадь — они также вводятся императивно и не «доказываются», в том числе из теоремы пифагора.
для школьной геометрии кроме аксиом евклида, предполагается (с какого-то лапласиана это им «очевидно») работа всей школьной алгебры(т.е. по факту к списку аксиом евклида и теоремы паша, добавляются аксиомы алгебры). в целом для «доказательства» теорем из школьной программы, кажется, евклидовой аксиоматики было достаточно (разве что, дополненная теоремой паша, которая там «подразумевалась», но из евклида явно вовсе не выводится).
ещё в школьной геометрии(могу ошибаться, но как помню) не выводится число «пи» оно задаётся как известное откуда-то, и формулы площадей круга, объёмов шара и площадь сферы вроде бы не выводились(возможно в курсе алгебры старших классов при интегрировании поднимался вопрос получения пи через ряды и формул площадей и объёмов через интегралы).
Прочитать ещё 1 ответ
Что такое аксиома пример геометрия?
На месте Евклида я бы начал так: Для упрощения расчетов (размышлений) будем строить геометрию на идеальной плоскости, реально не существующей в природе. Такую плоскость можно построить через любые три точки, не лежащие на одной прямой.А на этой плоскости через любые две точки можно провести одну прямую, уходящую в бесконечность. Через точку, не лежащую на этой прямой, можно провести параллельную ей и нигде и никогда с ней не пересекающейся. Вот,наверное, всё. И никаких аксиом и постулатов.
Прочитать ещё 1 ответ
Какое определение у точки ?
У вас такой набор хэштегов, что вы кажется даже не про геометрию, но будем думать, что все же про нее.
Следует дополнить ответ выше. Действительно, точка — не определяемое понятие. Но человек, не знакомый с математикой, возгласит: А почему мы её не определяем? Какая геометрия наука если она оперирует тем, что не может даже определить?
Углубимся в историю. Евклид(основатель геометрии, древнегреческий математик) в своих «Началах» таки определяет точку, как «то, часть чего есть ничто». Но согласитесь, это определение какое-то странное, непонятное. Так же Евклид определяет и другие основные понятия геометрии:
«Линия — длина без ширины. Края же линии — точки. Прямая линия есть та, которая равно лежит на всех своих точках. Поверхность есть то, что имеет только длину и ширину. Края же поверхности — линии. Плоская поверхность есть та, которая равно лежит на всех своих линиях.»
Ну очень странные определения. Эти определения — описательны и не конкретны. Например не понятно что такое длина и ширина в определении линии. Проблема также и в том, что ничего существенного из них не следует, никаких важный свойств, которые мы могли бы применить. Поэтому в геометрии есть требование к своим определениям, они должны быть конструктивны. Т.е. должны быть конкретны и из них должно следовать что-то существенное. В дальнейшей математики заметили, что эти определения не используются при доказательстве теорем(ведь из них ничего и не следует) поэтому их можно опустить, седлать не определяемыми.
Важнейшие свойства основных понятий (точка, прямая и т.д.), из которых что-то следует, описываются в аксиомах(кстати, неверно говорить, что это то, что не надо доказывать. Вернее будет сказать, что «Аксиома — это утверждение принимаемое в рамках нашей теории без доказательства». Так например есть геометрия Лобачевского где заместо аксиомы параллельности, взяли её отрицание, поэтому сама аксиома параллельности в ней неверна. Или числа(которые, кстати мы тоже строим аксиоматически), может определить разным набором аксиом, в каждом из которым аксиома из другого набора будет теоремой, которую еще предстоит доказывать). А через эти аксиомы построили Евклидову геометрию.
P.S. Прошу прощения за уход в сторону, но думаю, что и этот разговор не лишний.
Прочитать ещё 1 ответ

Общая характеристика
Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.
Основные понятия о составляющих
Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.

Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.
Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).
Виды линий:

- Замкнутая. Когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
- Разомкнутая. Начало и окончание не соединяются.
- Прямая. Обозначается буквой а или b.
- Ломаная. Заключается в соединенных отрезках не под углом 180 градусов. Линия обозначается перечислением всех вершин.
- Кривая.Отличная от прямой линии.
Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.
Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.
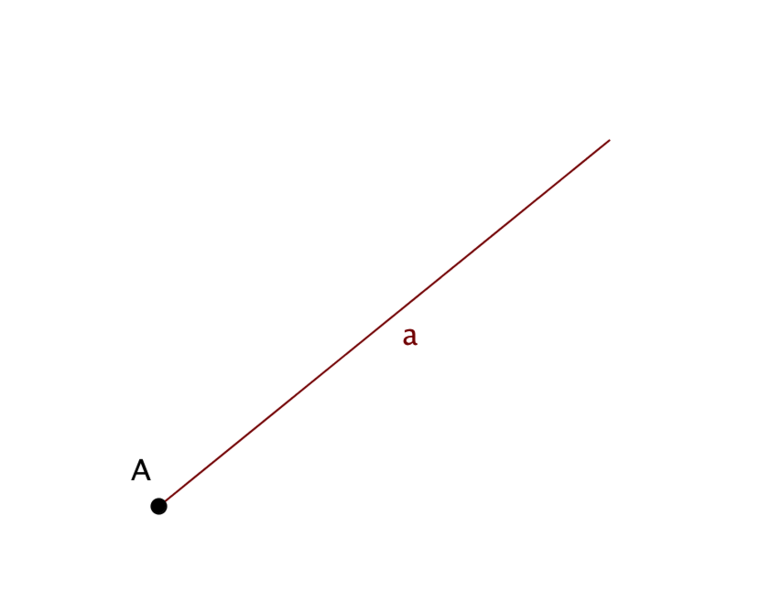
Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.
Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.
Стандартные объекты
К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.
Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.
Виды треугольника в зависимости от угла (У):
- Прямой. Один У будет прямым, два — менее 90 градусов.
- Острый. Градусная мера больше 0, но меньше 90 гр.
- Тупой. Один У тупой, два других будут острыми.
Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.
Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.
Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.
Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.
Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.
Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.
Сложные модели
В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.
Определение тела и пространства

Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.
Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).
Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.
В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).

Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.
Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.
Объемные фигуры:
- Шар.
- Конус.
- Параллелепипед.
- Цилиндр.
- Сфера.
Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.
Виды многогранников:
- Тетраэдер (четырехгранник). Это правильный треугольник.
- Куб (гексаэдр). Грани являются квадратом.
- Октаэдр. Имеется шесть вершин и восемь граней.
- Икосаэдр. Равносторонние треугольники являются гранями. Имеется 12 граней и 12 вершин.
- Додекаэдр. Правильные шестиугольники, имеется 12 граней, 20 вершин.
В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.
Познавательные игрушки детям
Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.
Основной материал для обучения детей:
- Яркие карточки с основными фигурами, формами. Шаблоны будут наглядным пособием перед школой.
- Раскраски, прописи, рабочая тетрадь. На каждой странице тетради представлены простейшие графические упражнения и задания. Выполняя их, малыш познакомится с геометрией и узнает названия фигур.
- Специальная детская литература.
Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.

Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.
Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.
Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.
Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.
Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.
