Свойства параллелограмма какой класс

В этом разделе мы рассматриваем геометрический объект параллелограмм. Все элементы параллелограмма наследуются от четырехугольника, поэтому рассматривать их мы не будем. А вот свойства и признаки заслуживают детального рассмотрения. Мы разберем:
- чем признак отличается от свойства;
- рассмотрим основные свойства и признаки, которые изучают в программе 8 класса;
- сформулируем еще два дополнительных свойства, которые получим при решении опорных задач.
2.1 Определение параллелограмма
Чтобы правильно давать определения понятиям в геометрии, нужно не просто их заучивать, а понимать, как они формируются. В этом деле нам хорошо помогают схемы родовых понятий. Давайте посмотрим, что это такое.
Наш учебный модуль называется «Четырехугольники» и четырехугольник является ключевым понятием в этом курсе. Мы можем дать следующее определение четырехугольнику:
Четырёхугольник-это многоугольник, у которого четыре стороны и четыре вершины.
В этом определении родовым понятием будет многоугольник. Теперь дадим определение многоугольнику:
Многоугольником называется простая замкнутая ломаная вместе с частью плоскости, которую она ограничивает.
Ясно, что родовым понятием здесь выступает понятие ломаная. Если мы пойдем далее, то придем к понятию отрезка, а затем к конечным понятиям точка и прямая. Таким же образом мы можем продолжить нашу схему вниз:

Если мы потребуем, чтобы у четырехугольника две стороны были параллельны, а две нет, то мы получим фигуру, которая называется трапецией.
Трапеция – четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
А в случае, когда все противоположные стороны параллельны, мы имеем дело с параллелограммом.
Параллелограмм – четырехугольник, у которого противоположные стороны параллельны.
2.2 Cвойства параллелограмма
Свойство 1. В параллелограмме противоположные стороны равны и противоположные углы равны.

Докажем это свойство.
Дано: ABCD — параллелограмм.
Доказать: $angle A = angle C, angle B = angle D, AB = CD, AD = BC.$
Доказательство:
При доказательстве свойств любого геометрического объекта всегда вспоминаем его определение. Итак, параллелограмм – четырехугольник, у которого противоположные стороны параллельны. Ключевым моментом здесь выступает параллельность сторон.
Построим секущую ко всем четырем прямым. Такой секущей будет диагональ BD.

Очевидно, что нужно рассмотреть углы, образованные секущей и параллельными прямыми. Так как прямые параллельны, то накрест лежащие углы равны.
Теперь можно увидеть два равных треугольника по второму признаку.
Из равенства треугольников непосредственно следует первое свойство параллелограмма.
Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.

Дано: ABCD — параллелограмм.
Доказать: $AO = OC, BO = OD.$
Доказательство:
Логика доказательства здесь такая же, как и в предыдущем свойстве: параллельность сторон и равенство треугольников. Первый шаг доказательства тот же, что у первого свойства.
Вторым шагом мы доказываем равенство треугольников по второму признаку. Обратите внимание, что равенство $BC=AD$ можно принять без доказательства (используя Свойство 1).
Из этого равенства следует, что $AO = OC, BO = OD.$

2.3 Опорная задача №4 (Свойство угла между высотами параллелограмма)

Дано: ABCD — параллелограмм, BK и BM — его высоты, $angle KBM = 60^0$.
Найти: $angle ABK$, $angle A$
Решение:
Приступая к решению этой задачи, нужно иметь ввиду следующее:
высота в параллелограмме перпендикулярна обеим противоположным сторонам
Например, если отрезок $BM$ проведен к стороне $DC$ и является его высотой ($BM perp DC$), то этот же отрезок будет высотой к противположной стороне ($BM perp BA$). Это следует из параллельности сторон $AB parallel DC$.

Далее мы можем найти $angle A$ из прямоугольного $bigtriangleup ABK$: $angle A = 90^0-30^0=60^0$

При решении этой задачи, ценным является свойство, которое мы получаем.
Дополнительное свойство. Угол между высотами параллелограмма, проведенными из его вершины, равен углу при соседней вершине.
2.4 Опорная задача №5 (Свойство биссектрисы параллелограмма)

Биссектриса угла А параллелограмма ABCD пересекает сторону BC в точке L, AD=12 см, AB =10 см.
Найти длину отрезка LC.
Решение:
- $angle 1 = angle 2$ (АК — биссектрисса);
- $angle 2 = angle 3$ (как накрест лежащие углы при $AD parallel BC$ и секущей АL);
- $angle 1 = angle 3$, $bigtriangleup ABL -$ равнобедренный.
Далее несложно найти длину отрезка LC = 2 см.
По ходу решения задачи мы получили свойство:
Дополнительное свойство. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Тема и номер урока в теме: Параллелограмм, №1
Предмет математика
Класс 6
Базовый учебник : Учебник: Математика. Арифметика. Геометрия. 6 класс: учеб.для общеобразовательных учреждений с приложением на электронном носителе / Е.А. Бунимович и др. –2-е изд. – М.: Просвещение, 2013. – 223 с.: ил. – (Академический школьный учебник)
(Сферы)
Цели урока:
образовательная– обобщение и развитие знаний обучающихся о геометрических фигурах группы многоугольников и их свойствах, формирование навыка применения полученных знаний в жизненных ситуациях.
развивающая – развитие логического мышления, математического аппарата, познавательного интереса к предмету, самостоятельности; читательских компетенций.
воспитательная – формирование морально-этической стороны личности, эстетического сознания, научной эстетики; тренировка стрессоустойчивости.
2.Задачи:
— образовательные (формирование познавательных УУД):
применять знания о многоугольниках, уметь выделять данный тип из многообразия геометрических фигур, определять их общие свойства, изображать их на плоскости.
— воспитательные (формирование коммуникативных и личностных УУД):
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи; понимать смысл поставленной задачи; слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.
— развивающие (формирование регулятивных УУД)
развивать умение анализировать, сравнивать, обобщать, делать выводы, самостоятельно ставить цели, развивать внимание, формировать коммуникативную компетенцию учащихся; выбирать способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия, контроль и оценка процесса и результатов деятельности.
3. Методы:
по источникам знаний: словесные, наглядные;
по степени взаимодействия учитель-ученик: эвристическая беседа;
относительно дидактических задач: подготовка к восприятию;
относительно характера познавательной деятельности: репродуктивный, частично-поисковый.
4.Планируемые результаты: Распознавать на чертежах рисунках в окружающем мире параллелограммы. Изображать параллелограммы с использованием чертежных инструментов. Исследовать свойства параллелограмма используя эксперимент, наблюдение, измерение, моделирование. Использовать компьютерное моделирование и эксперимент для изучения свойств параллелограмма. Формулировать, обосновывать и опровергать с помощью контрпримеров утверждения о свойствах параллелограмма. Сравнивать свойства параллелограмма различных видов: ромба, квадрата, прямоугольника.
5. Оборудование: Учебник: Математика. Арифметика. Геометрия. 6 класс: учеб. для общеобразовательных учреждений с приложением на электронном носителе / Е.А. Бунимович и др. –2-е изд. – М.: Просвещение, 2013. – 223 с.: ил. – (Академический школьный учебник) (Сферы), Тетрадь-тренажер Математика. Арифметика. Геометрия. 6 класс: пособие для учащихся общеобразовательных учреждений/ Е.А. Бунимович и др. – 3-е изд. – М.: Просвещение, 2013. – 128 с.: ил., мультимедиа проектор, компьютер, рабочие тетради учащихся, раздаточный материал (калька, модели квадрата, прямоугольника, ромба), циркуль.
6. Тип и особенности: урок открытия и изучения новых знаний через экспериментальную проверку, с помощью наблюдений. Урок в форме эвристической беседы
7. Формы работы учащихся:Фронтальная, парная, индивидуальная.
8. Структура урока
Класс 6. Урок № 143 Тема: «Параллелограмм и его свойства»
Этапы урока
Задачи этапа
Визуальный ряд
Деятельность учителя
Деятельность учащихся
Формируемые УУД
Организационный этап
Создать благоприятный психологический настрой на работу
На доске дата и название темы: «Параллелограмм и его свойства»
Приветствие обучающихся.
Проверка учителем готовности класса к уроку; организация внимания.
Личностные —умение выделять нравственный аспект поведения
Коммуникативные — умение слушать
Регулятивные –организовать себя, настроиться на работу.
Актуализация знаний и умений
Определить цель занятия
Продемонстрировать необходимость знания точного определения
На столах учащихся открыт учебник с. 206 п. 44
Рубрика «Вы узнаете»
Какой четырехугольник называется параллелограммом.
Какими свойствами обладает параллелограмм
Какие выделяют виды параллелограммов
Заготовленные в лаборатории ЭП различного вида четырехугольники
— Слева на странице учебника 204 обозначена цель сегодняшнего занятия. Сформулируйте, ребята, что мы сегодня должны узнать?
Читают рубрику.
Содержание рубрики:
Какой четырехугольник называется параллелограммом.
Какими свойствами обладает параллелограмм
Какие выделяют виды параллелограммов
Регулятивные – прогнозирование своей деятельности. Выделение и осознание того, что уже пройдено.Постановка учебной задачи на основе известного
Познавательные—поиск и выделение необходимой информации. Логический анализ объектов с целью выделения признаков.
Коммуникативные — умение с достаточной полнотой и точностью выражать свои мысли, слушать и вступать в диалог
Личностные — самоопределение ,смыслообразование.
— Для изучения данной темы нам необходимо вспомнить:
какие вы знаете многоугольники; какие прямые называются параллельными.
— Многоугольники бывают: треугольники, четырехугольники (прямоугольник, квадрат).
— Параллельными называются прямые, которые не пересекаются
— А каким инструментом мы можем построить многоугольник и параллельные прямые
— С помощью линейки и чертежного треугольника
— Из приведённых в лаборатории четырехугольников, как вы считаете какие могут быть названы параллелограммом?
ABCD; MNKF; QPER
Рубрика «Математический блокнот»
— Слово параллелограмм – греческого происхождения, в переводе оно означает «изображающийся параллельными»
— Как Вы считаете все ли названные вами четырехугольники можно назвать параллелограммами?
ABCD- параллелограмм
MNKF- нет
QPER- параллелограмм
Целеполагания (построение отрезков циркулем и линейкой) в новой теме.
Объяснение материала
Флеш-определение ЭП
— Давайте прослушаем определение параллелограмма и изобразим эту фигуру в тетради (1 часть флеш — демонстрации)
Просмотр флеш-демонстрации (определение параллелограмма)
Изображают параллелограмм
Познавательные-поиск и выделение необходимой информации. Структурирование знаний. Анализ объектов. Построение логической цепи рассуждений
Регулятивные-планирование, прогнозирование
Коммуникативные—
умение слушать и вступать в диалог
— Теперь рассмотрим свойства параллелограмма. Для этого проведем эксперимент (2 часть флеш-демонстрации) свойство симметрии.
Учащиеся работают в соответствии с флеш – демонстрацией (свойство симметрии параллелограмма)
Эксперимент с калькой позволяет нам открыть и другие свойства параллелограмма:
При повороте противоположные стороны и углы параллелограмма «поменялись местами». Какой можно сделать вывод?
При повороте отрезки ОА и ОС, а также ОD и ОВ поменялись местами. Каждая диагональ займет свое место.
Какой можно сделать вывод об отрезках диагоналей?
Посмотрим, что данное свойство дает нам удобный способ построения параллелограмма.
Вывод:
Противоположные стороны равны
Вывод:
Противоположные углы равны
Вывод:
Диагонали точкой О делятся пополам.
Просмотр флеш-демонстрации (построение параллелограмма с помощью свойств диагоналей)
Применение ранее изученного, повторение
Демонстрация этапов проведения эксперимента
Виды параллелограммов
Ребята, прямоугольник, ромб, квадрат также являются параллелограммами
Просмотр флеш-демонстрации (виды параллелограммов)
Познавательные- понимание и выделение необходимой информации. Структурирование знаний. Анализ объектов.
Регулятивные-планирование своей деятельности для решения поставленной задачи и контроль полученного результата
Коммуникативные— обмен знаниями между членами группы для принятия эффективных совместных решений
Личностные– развитие навыков сотрудничества
Работа с моделями (на столах модели: квадрат, прямоугольник, ромб)
Работа в парах.
Учитель раздаёт каждой паре по три модели четырехугольников.
(Приложение 1)
Задание 1.
Ребята, используя перегибы моделей по диагоналям, убедитесь, что данные четырехугольники имеют те же свойства что и параллелограмм.
Задание 2
Можете ли вы назвать свойства данных фигур, отличающиеся от свойств параллелограмма?
Работают в парах.
Выполняют перегибы, анализируют и делают выводы, контролируя действия друг другу.
Результаты исследования, высказываются парами и обобщаются.
Использование нового алгоритма и приведение аргументов
Актуализировать необходимость выполнения правдоподобных, точных построений
Работа с учебником
А теперь поработаем по учебникам
Выполним № 685 стр. 208 (устно), № 693 стр. 209
№ 685
ABTF; ACDF; BCDE.
№ 693
Отвечают на вопросы (устно), в тетрадях выполняют рисунки.
Познавательные-выделение и формулирование познавательной цели, рефлексия способов и условий действия.Анализ и синтез объектов.
Регулятивные— планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, саморегуляция
Коммуникативные-умение слушать и вступать в диалог, коллективное обсуждение проблем (при необходимости)
Личностные-анализ речевыхконструкций
Выполнение заданий из тетради- тренажера
Работаем с тренажером
стр. 130 № 290
№ 290 учащимся необходимо проанализировать и опровергнуть утверждения с помощью контрпримера
Подведение итогов урока
Дать качественную оценку работы класса и отдельных обучаемых
На партах открыты стр. 207 учебника, на экране тоже -рубрика «Вопросы и задания»
— На какой из вопросов Рубрики «Вы узнаете» вы получили ответ сегодня на уроке, и на какие вопросы раздела «Вопросы и задания» вы можете теперь ответить.
Указывают, читают и отвечают на вопросы
рубрики
Познавательные-выделение и формулирование познавательной цели, рефлексия способов и условий действия.
Регулятивные-оценка промежуточных результатов и саморегуляция для повышения мотивации учебной деятельности
Коммуникативные— участие в коллективном обсуждении проблем.
Личностные-жизненное самоопределение, ценносто-смысловая ориентация обучающихся
Информирования о домашней работе
Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания.
Работа с учебником и тетрадью —
тренажером
Учебник: Глава 11 п. 44, стр. 206 – 207 № 687, 895
Тренажер: стр. 131 № 293
Познавательные—
поиск и выделение необходимой информации
Регулятивные— оценка промежуточных результатов и саморегуляция для повышения мотивации учебной деятельности
Личностные-нравственно -этическая ориентация
Работа дома с текстом по карточкам.
Сказка (Приложение 2)
Собрались все четырехугольники на лесной поляне и стали обсуждать вопрос о выборе своего короля. Долго спорили и никак не могли прийти к единому мнению. И вот один старый параллелограмм сказал: «Давайте все отправимся в царство четырехугольников. Кто первым придет, тот и будет королем» Все согласились. Рано утром отправились все в далекое путешествие. На пути путешественников повстречалась река, которая сказала: «Переплывут меня только те, у кого диагонали пересекаются и точкой пересечения делятся пополам» Часть четырехугольников осталась на берегу, остальные благополучно переплыли и отправились дальше. На пути им повстречалась высокая гора, которая сказала, что даст пройти только тем, у кого диагонали равны. Несколько путешественников осталась у горы, остальные продолжили путь. Дошли до большого обрыва, где был узкий мост. Мост сказал, что пропустит тех, у кого диагонали пересекаются под прямым углом. По мосту прошел только один четырехугольник, который первым добрался до царства и был провозглашен королем.
1. Кто стал королем?
2. Кто был его основным соперником?
3. Кто первым вышел из соревнования?
Рефлексии
Инициировать рефлексию детей по поводу психоэмоционального состояния, мотивации, их собственной деятельности и взаимодействия с учителем и другими детьми в классе
Если вы считаете, что вы поняли тему сегодняшнего урока, то хлопните три раза в ладоши.
Если вы считаете, что не достаточно усвоили материал, то хлопните всего один раз.
Если вы считаете, что вы не поняли тему сегодняшнего урока, то хлопать не надо.
Вы аплодировали себе и своим новым знаниям. Спасибо за урок.
Регулятивные—оценка своей деятельности и других
Личностные-смыслообразование
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
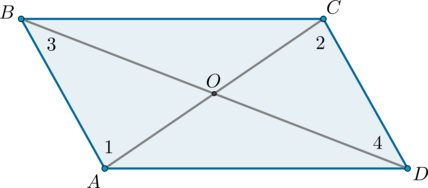
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
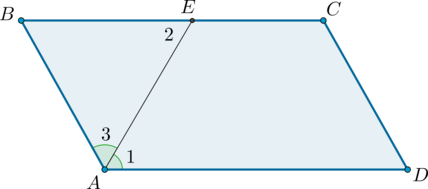
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
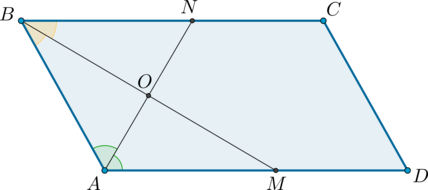
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ — (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).
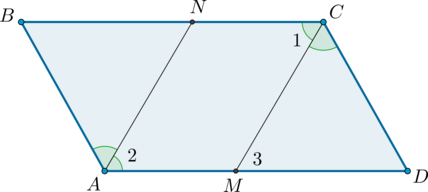
Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).



