Свойства касательной к окружности в каком классе

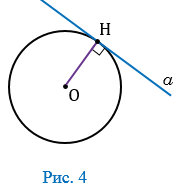
Касательная к окружности — прямая, имеющая с окружностью одну общую точку, которая называется точкой касания прямой и окружности. На рисунке 1 прямая — касательная к окружности, точка Н — точка касания прямой и окружности с центром в точке О.

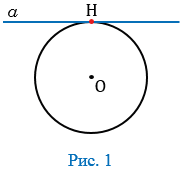
Свойство касательной к окружности

Теорема

Доказательство

Дано: — касательная к окружности с центром в точке О, Н — точка касания (Рис. 2).

Доказать: ОН.

Доказательство:

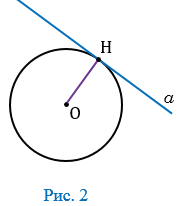
Предположим, что ОН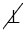. Тогда радиус ОН является наклонной к прямой . При этом перпендикуляр, проведенный из точки О к прямой , меньше наклонной ОН, тогда расстояние от центра О окружности до прямой меньше радиуса. Следовательно прямая и окружность будут иметь две общие точки, что противоречит условию: прямая — касательная. Поэтому наше предположение неверно, значит, ОН . Теорема доказана.

Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Доказательство

Дано: АВ и АС — касательные к окружности с центром в точке О, В и С — точки касания (Рис. 3).

Доказать: АВ = АС и 3 =4.

Доказательство:

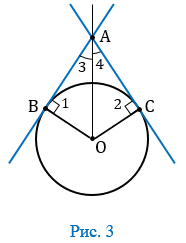
1 =2 = 900, т.к. ОВАВ, ОСАС по теореме о свойстве касательной (смотри выше), поэтому 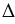АВО и 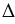АСО прямоугольные. При этом ОВ = ОС (радиусы), АО — общая, следовательн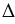о, АВО =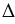АСО (по гипотенузе и катету). Из равенства треугольников следует, что АВ = АС и 3 =4. Что и требовалось доказать.

Теорема, обратная теореме о свойстве касательной (признак касательной)

Теорема

Доказательство

Дано: ОН — радиус окружности с центром в точке О, Н, ОН (Рис. 4).

Доказать: — касательная.

Доказательство:

По условию радиус ОН , поэтому расстояние от центра окружности до прямой равно радиусу, и, следовательно, прямая и окружность имеют только одну общую точку, значит, данная прямая является касательной к окружности (по определению касательной). Теорема доказана.

Задача

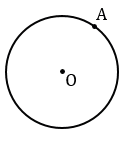
Через данную точку А окружности с центром О провести касательную к этой окружности.

Дано: точка А лежит на окружности с центром в точке О.

Провести касательную к окружности так, что А.

Решение:

Строим с помощью циркуля окружность с центром в точкеО, отмечаем на данной окружности точку А.

Далее проводим прямую ОА и строим прямую , проходящую через точку А перпендикулярно к прямой ОА. Для этого с помощью циркуля строим окружность произвольного радиуса с центром в точке А (всю окружность строить необязательно, смотри выделенное красным). Точки пересечения данной окружности с прямой ОА обозначаем буквами В и С.

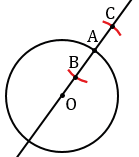
Затем строим две окружности радиуса ВС с центрами в точках В и С (полностью окружности строить необязательно, смотри выделенное синим и зеленым цветом). Данные окружности пересекаются в двух точках, обозначим их Р и Q. Через точки Р и Q с помощью линейки проводим прямую , которая будет перпендикулярна к прямой ОА.

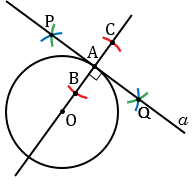
Итак, ОА, ОА — радиус, следовательно, — искомая касательная к окружности с центром в точке О радиуса ОА (по признаку касательной).

Описание презентации по отдельным слайдам:

Инфолавка — книжный магазин для педагогов и родителей от проекта «Инфоурок»

Проверен экспертом

Общая информация

Вам будут интересны эти курсы:

Учитель Хильченко Е.П. УРОК №____ КЛАСС___________ ДАТА______________

«Касательная к окружности и её свойства»

Цели:

Образовательные: ввести понятие касательной, точки касания,

рассмотреть свойство касательной и её признак; обеспечить овладение основными алгоритмическими приёмами построения касательной к окружности; сформировать умения применять теоретические знания к решению задач.

Развивающие: развитие мышления и математической речи.

Воспитательные: работать над формированием умений наблюдать, подмечать закономерности, обобщать, проводить рассуждения по аналогии,

привитие интереса к математике.

Требования к уроку: знать понятие касательной к окружности, точки касания, свойство касательной и её признак; уметь строить касательную к окружности; уметь применять знания при решении задач.

Тип урока: урок сообщения и усвоения новых знаний.

Формы работы: индивидуальная, фронтальная.

Методы: частично-поисковые, наглядные, словесные.

Оборудование: карточки с заданиями, циркуль, треугольник, линейка, презентация.

Структура урока:

1. Организационный момент.

2. Актуализация знаний.

— повторение изученного материала;

— подготовка к восприятию нового материала.

3. Объяснение новой темы.

4. Закрепление нового материала.

5. Самостоятельная работа.

6. Домашнее задание.

7. Подведение итогов.Ход урока

1. Организационный момент. (1мин)

Учитель: Здравствуйте, ребята. Этот урок мы посвятим изучению свойства касательной к окружности, научимся строить её, а также научимся применять теоретические знания к решению задач.(Учащиеся записывают тему) Давайте сначала отметим отсутствующих и повторим материал прошлого урока.

Учитель фиксирует отсутствующих.

2. Актуализация знаний.

-повторение изученного материала(5 мин.):

Учитель задает учащимся вопросы.

1.Что такое окружность, радиус окружности?

2. Какие случаи взаимного расположения прямой и окружности могут быть?

3. Прокомментируйте каждый случай.

На 1, 2 вопросы отвечают по одному ученику; на 3 три ученика. Остальные учащиеся могут дополнят товарищей.

После ответы проверяются с помощью презентации (слайд 2)

— подготовка к восприятию нового материала(2-3 мин):

Учитель: В тетради начертите окружность произвольного радиуса с центром в точке О, проведите три прямые, так чтобы получилось разное количество общих точек у прямой и окружности.

Один ученик выполняет задание у доски.

Обозначим прямые и полученные точки:

a,b,c и С,В,H.

Повторить

d

d>r нет общих точек

d=r 1 общая точка

3. Объяснение новой темы. (10мин.)

Учитель: На этом уроке мы рассмотрим свойства окружности и прямой c.

1. Работа с учебником.

Учитель: На страница 159 найдите и прочитайте определение касательной к окружности.

После один ученик читает вслух, остальные слушают, учитель комментирует (слайд 3)

Определение. Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности.

Учащиеся называют на рисунке точку касания и прямую касательную к окружности.

(C- точка касания, прямая с – касательная к окружности)

Все это фиксируется в тетрадях учащихся.

Учитель: Какими же свойствами обладает эта прямая? Чтобы ответить на этот вопрос, проведите отрезок соединяющий центр окружности и точку касания, измерьте получившийся угол.

Ученики измеряют получившийся угол.(90)

Учитель: Что можно сказать о касательной и радиусе?

Учащиеся: Они перпендикулярны.

Учитель: Правильно, молодцы. А теперь давайте прочитаем теорему.

2. Теорема: Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.(слайд 4)

Доказательство разбирается в ходе беседы.

Учащиеся делают новый чертёж.

Допустим, что прямая р не перпендикулярна к радиусу ОА(На рисунке сделать построение другим цветом). Сравните расстояние от центра окружности до прямой р с радиусом окружности.

Назовите перпендикуляр к прямой р (ОВ) и наклонную (ОА)

Ученики называют перпендикуляр к прямой и наклонную.

Учитель: Расстояние от точки О до прямой р , это ОВ, меньше радиуса окружности ОА, который в данном случае будет являться наклонной по отношению к прямой р, а расстояние от точки О до прямой р – перпендикуляр, а, как известно, любая наклонная больше перпендикуляра, проведённого из той же точки к той же прямой, т. е. ОВ<ОА.

Учитель: Сколько тогда общих точек у прямой р и окружности?

Учащиеся: 2

Учитель: Может ли прямая р быть касательной к окружности? Почему?

Учащиеся: Т.к. прямая р имеет две общие точки с окружностью, то она не может быть касательной по определению.

Учитель: Верно ли предположение, что прямая р не перпендикулярна радиусу окружности? О чём это говорит?

Учащиеся: Предположение не верно, следовательно прямая р перпендикулярна радиусу ОА.

3. Теперь запишем это доказательство в тетради.

Дано: окр. (О; r=ОА), р-касательная

A к окружности, А-точка касания.

Доказать: рОА.

Доказательство:

Предположим, что рОА, тогда ОА наклонная к прямой р, а ОВр, т. к. ОВ<ОА, то расстояние от центра окружности О до прямой р меньше радиуса, следовательно прямая р и окружность имеют две общие точки, что противоречит условию: прямая р – касательная, т. о. р ОА. Теорема доказана.

4. Закрепление нового материала (13 мин)

1.Решите задачи.(слайд 6)(6 мин)

Задания выполняются на доске учащимися, учитель по необходимости помогает им.

2. Гимнастика для глаз. (2мин)

Глубоко вдохните, зажмурив глаза как можно сильнее. Напрягите мышцы шеи, лица, головы. Задержите дыхание на 2-3 секунды, потом быстро выдохните, широко раскрыв на выдохе глаза. Повторить 5 раз.

Закройте глаза, помассируйте надбровные дуги и нижние части глазниц круговыми движениями — от носа к вискам.

Закройте глаза, расслабьте брови. Повращайте глазными яблоками слева направо и справа налево. Повторить 5 раз.

Поставьте большой палец руки на расстоянии 25-30 см. от глаз, смотрите двумя глазами на конец пальца 3-5 секунд, закройте один глаз на 3-5 секунд, затем снова смотрите двумя глазами, закройте другой глаз. Повторить 5 раз.

3. Построение касательной. (5 мин.)

Ученик, подготовленный заранее, объясняет построение касательной к окружности в заданной точке. Учащиеся выполняют построение в тетради.

Дано: окружность, О — центр, А — лежит на окружности.

Построить касательную к окружности в точке А.

Построение:

ОА – прямая.

От точки А отложим ОА=ОА.

Из точек О и О проведём окружности, радиусом большим ОА.

Через точки пересечения окружностей проведём прямую а.

Прямая а будет касательной по определению.

Самостоятельная работа.(8 мин)

Учитель: А теперь, ребята, чтобы закрепить ваши полученные сегодня на уроке знания сделаем самостоятельную работу.

6. Д?