От каких свойств маятника зависит его угловая скорость
Механическая система, которая состоит из материальной точки (тела), висящей на нерастяжимой невесомой нити (ее масса ничтожно мала по сравнению с весом тела) в однородном поле тяжести, называется математическим маятником (другое название – осциллятор). Бывают и другие виды этого устройства. Вместо нити может быть использован невесомый стержень. Математический маятник может наглядно раскрыть суть многих интересных явлений. При малой амплитуде колебания его движение называется гармоническим.
Общие сведения о механической системе

Формула периода колебания этого маятника была выведена голландским ученым Гюйгенсом (1629-1695 гг.). Этот современник И. Ньютона очень увлекался данной механической системой. В 1656 г. он создал первые часы с маятниковым механизмом. Они измеряли время с исключительной для тех времен точностью. Это изобретение стало важнейшим этапом в развитии физических экспериментов и практической деятельности.
Если маятник находится в положении равновесия (висит отвесно), то сила тяжести будет уравновешиваться силой натяжения нити. Плоский маятник на нерастяжимой нити является системой с двумя степенями свободы со связью. При смене всего одного компонента меняются характеристики всех ее частей. Так, если нитку заменить на стержень, то у данной механической системы будет всего 1 степень свободы. Какими же свойствами обладает математический маятник? В этой простейшей системе под воздействием периодического возмущения возникает хаос. В том случае, когда точка подвеса не двигается, а совершает колебания, у маятника появляется новое положение равновесия. При быстрых колебаниях вверх-вниз эта механическая система приобретает устойчивое положение «вверх тормашками». У нее есть и свое название. Ее называют маятником Капицы.
Свойства маятника
Математический маятник имеет очень интересные свойства. Все они подтверждаются известными физическими законами. Период колебаний любого другого маятника зависит от разных обстоятельств, таких как размер и форма тела, расстояние между точкой подвеса и центром тяжести, распределение массы относительно данной точки. Именно поэтому определение периода висящего тела является довольно сложной задачей. Намного легче вычисляется период математического маятника, формула которого будет приведена ниже. В результате наблюдений над подобными механическими системами можно установить такие закономерности:
• Если, сохраняя одинаковую длину маятника, подвешивать различные грузы, то период их колебаний получится одинаковым, хотя их массы будут сильно различаться. Следовательно, период такого маятника не зависит от массы груза.
• Если при запуске системы отклонять маятник на не слишком большие, но разные углы, то он станет колебаться с одинаковым периодом, но по разным амплитудам. Пока отклонения от центра равновесия не слишком велики, колебания по своей форме будут достаточно близки гармоническим. Период такого маятника никак не зависит от колебательной амплитуды. Это свойство данной механической системы называется изохронизмом (в переводе с греческого «хронос» — время, «изос» — равный).
Период математического маятника
Этот показатель представляет собой период собственных колебаний. Несмотря на сложную формулировку, сам процесс очень прост. Если длина нити математического маятника L, а ускорение свободного падения g, то эта величина равна:
T = 2π√L/g
Период малых собственных колебаний ни в какой мере не зависит от массы маятника и амплитуды колебаний. В этом случае маятник двигается как математический с приведенной длиной.
Колебания математического маятника
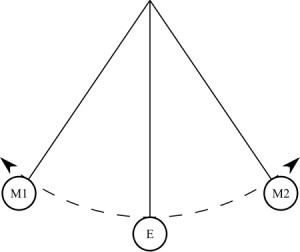
Математический маятник совершает колебания, которые можно описать простым дифференциальным уравнением:
x + ω2 sin x = 0,
где х (t) – неизвестная функция (это угол отклонения от нижнего положения равновесия в момент t, выраженный в радианах); ω – положительная константа, которая определяется из параметров маятника (ω = √g/L, где g – это ускорение свободного падения, а L – длина математического маятника (подвес).
Уравнение малых колебаний вблизи положення равновесия (гармоническое уравнение) выглядит так:
x + ω2 sin x = 0
Колебательные движения маятника
Математический маятник, который совершает малые колебания, двигается по синусоиде. Дифференциальное уравнение второго порядка отвечает всем требованиям и параметрам такого движения. Для определения траектории необходимо задать скорость и координату, из которых потом определяются независимые константы:
x = A sin (θ0 + ωt),
где θ0 – начальная фаза, A – амплитуда колебания, ω – циклическая частота, определяемая из уравнения движения.
Математический маятник (формулы для больших амплитуд)
Данная механическая система, совершающая свои колебания со значительной амплитудой, подчиняется более сложным законам движения. Для такого маятника они рассчитываются по формуле:
sin x/2 = u * sn(ωt/u),
где sn — синус Якоби, который для u < 1 является периодической функцией, а при малых u он совпадает с простым тригонометрическим синусом. Значение u определяют следующим выражением:
u = (ε + ω2)/2ω2,
где ε = E/mL2 (mL2 – энергия маятника).
Определение периода колебания нелинейного маятника осуществляется по формуле:
T = 2π/Ω,
где Ω = π/2 * ω/2K(u), K – эллиптический интеграл, π — 3,14.
Движение маятника по сепаратрисе
Сепаратрисой называют траекторию динамической системы, у которой двумерное фазовое пространство. Математический маятник движется по ней непериодически. В бесконечно дальнем моменте времени он падает из крайнего верхнего положения в сторону с нулевой скоростью, затем постепенно набирает ее. В конечном итоге он останавливается, вернувшись в исходное положение.
Если амплитуда колебаний маятника приближается к числу π, это говорит о том, что движение на фазовой плоскости приближается к сепаратрисе. В этом случае под действием малой вынуждающей периодической силы механическая система проявляет хаотическое поведение.
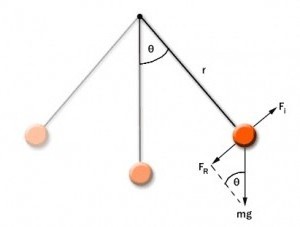
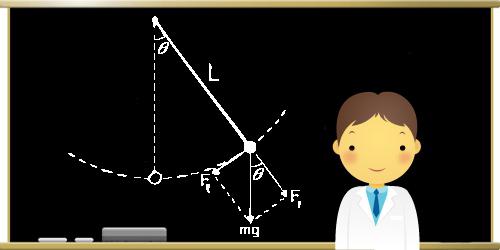
При отклонении математического маятника от положения равновесия с некоторым углом φ возникает касательная силы тяжести Fτ = –mg sin φ. Знак «минус» означает, что эта касательная составляющая направляется в противоположную от отклонения маятника сторону. При обозначении через x смещения маятника по дуге окружности с радиусом L его угловое смещение равняется φ = x/L. Второй закон Исаака Ньютона, предназначенный для проекций вектора ускорения и силы, даст искомое значение:
mg τ = Fτ = –mg sin x/L
Исходя из этого соотношения, видно, что этот маятник представляет собой нелинейную систему, поскольку сила, которая стремится вернуть его в положение равновесия, всегда пропорциональна не смещению x, а sin x/L.
Только тогда, когда математический маятник осуществляет малые колебания, он является гармоническим осциллятором. Иными словами, он становится механической системой, способной выполнять гармонические колебания. Такое приближение практически справедливо для углов в 15–20°. Колебания маятника с большими амплитудами не является гармоническим.
Закон Ньютона для малых колебаний маятника

Если данная механическая система выполняет малые колебания, 2-й закон Ньютона будет выглядеть таким образом:
mg τ = Fτ = –m* g/L* x.
Исходя из этого, можно заключить, что тангенциальное ускорение математического маятника пропорционально его смещению со знаком «минус». Это и является условием, благодаря которому система становится гармоническим осциллятором. Модуль коэффициента пропорциональности между смещением и ускорением равняется квадрату круговой частоты:
ω02 = g/L; ω0 = √ g/L.
Эта формула отражает собственную частоту малых колебаний этого вида маятника. Исходя из этого,
T = 2π/ ω0 = 2π√ g/L.
Вычисления на основе закона сохранения энергии
Свойства колебательных движений маятника можно описать и при помощи закона сохранения энергии. При этом следует учитывать, что потенциальная энергия маятника в поле тяжести равняется:
E = mg∆h = mgL(1 – cos α) = mgL2sin2 α/2
Полная механическая энергия равняется кинетической или максимальной потенциальной: Epmax = Ekmsx = E
После того как будет записан закон сохранения энергии, берут производную от правой и левой частей уравнения:
Ep + Ek = const
Поскольку производная от постоянных величин равняется 0, то (Ep + Ek)’ = 0. Производная суммы равняется сумме производных:
Ep’ = (mg/L*x2/2)’ = mg/2L*2x*x’ = mg/L*v + Ek’ = (mv2/2) = m/2(v2)’ = m/2*2v*v’ = mv* α,
следовательно:
Mg/L*xv + mva = v (mg/L*x + m α) = 0.
Исходя из последней формулы находим: α = — g/L*x.
Практическое применение математического маятника
Ускорение свободного падения изменяется с географической широтой, поскольку плотность земной коры по всей планете не одинакова. Там, где залегают породы с большей плотностью, оно будет несколько выше. Ускорение математического маятника нередко применяют для геологоразведки. В его помощью ищут различные полезные ископаемые. Просто подсчитав количество колебаний маятника, можно обнаружить в недрах Земли каменный уголь или руду. Это связано с тем, что такие ископаемые имеют плотность и массу больше, чем лежащие под ними рыхлые горные породы.
Математическим маятником пользовались такие выдающиеся ученые, как Сократ, Аристотель, Платон, Плутарх, Архимед. Многие из них верили в то, что эта механическая система может влиять на судьбу и жизнь человека. Архимед использовал математический маятник при своих вычислениях. В наше время многие оккультисты и экстрасенсы пользуются этой механической системой для осуществления своих пророчеств или поиска пропавших людей.
Известный французский астроном и естествоиспытатель К. Фламмарион для своих исследований также использовал математический маятник. Он утверждал, что с его помощью ему удалось предсказать открытие новой планеты, появление Тунгусского метеорита и другие важные события. Во время Второй мировой войны в Германии (г. Берлин) работал специализированный Институт маятника. В наши дни подобными исследованиями занят Мюнхенский институт парапсихологии. Свою работу с маятником сотрудники этого заведения называют «радиэстезией».
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки на конце невесомой нерастяжимой нити или лёгкого стержня и находящуюся в однородном поле сил тяготения[1]. Другой конец нити (стержня) обычно неподвижен. Период малых собственных колебаний маятника длины L, подвешенного в поле тяжести, равен
и не зависит, в первом приближении, от амплитуды колебаний и массы маятника. Здесь g — ускорение свободного падения.
Математический маятник служит простейшей моделью физического тела, совершающего колебания: она не учитывает распределение массы. Однако реальный физический маятник при малых амплитудах колеблется так же, как математический с приведённой длиной.
Характер движения маятника[править | править код]
Математический маятник со стержнем способен колебаться только в какой-то одной плоскости (вдоль какого-то выделенного горизонтального направления) и, следовательно, является системой с одной степенью свободы. Если же стержень заменить на нерастяжимую нить, получится система с двумя степенями свободы (так как становятся возможными колебания по двум горизонтальным координатам).
При колебаниях в одной плоскости маятник движется по дуге окружности радиуса , а при наличии двух степеней свободы может описывать кривые на сфере того же радиуса[1]. Нередко, в том числе в случае нити, ограничиваются анализом плоского движения; оно и рассматривается далее.
Уравнение колебаний маятника[править | править код]
Колебания математического маятника описываются обыкновенным дифференциальным уравнением (ДУ) вида
где ― положительная константа, определяемая исключительно из параметров маятника.
Неизвестная функция ― это угол отклонения маятника в момент от нижнего положения равновесия, выраженный в радианах; , где ― длина подвеса, ― ускорение свободного падения.
Уравнение малых колебаний маятника около нижнего положения равновесия (т. н. гармоническое уравнение) имеет вид:
Приведённые уравнения предполагают, что потерь энергии в системе нет.
Решения уравнения движения[править | править код]
Гармонические колебания[править | править код]
Малые колебания маятника являются гармоническими. Это означает, что смещение маятника от положения равновесия изменяется во времени по синусоидальному закону[2]. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимые константы:
где — амплитуда колебаний маятника, — начальная фаза колебаний, — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями.
Нелинейный маятник[править | править код]
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где — это синус Якоби. Для он является периодической функцией, при малых совпадает с обычным тригонометрическим синусом.
Параметр определяется выражением
где — энергия маятника в единицах t−2.
Период колебаний нелинейного маятника составляет
где K — эллиптический интеграл первого рода.
Для вычислений практически удобно разлагать эллиптический интеграл в ряд:
,
где — период малых колебаний, — максимальный угол отклонения маятника от вертикали.
При углах до 1 радиана (≈60°) с приемлемой точностью (ошибка менее 1 %) можно ограничиться первым приближением:
Точная формула периода, с квадратичной сходимостью для любого угла максимального отклонения, обсуждается на страницах сентябрьского выпуска журнала «Заметки американского математического общества» 2012 года[3]:
где — арифметико-геометрическое среднее чисел 1 и .
Движение по сепаратрисе[править | править код]
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, а затем останавливается, возвратившись в исходное положение.
Факты[править | править код]
Несмотря на свою простоту, математический маятник связан с рядом интересных явлений.
- Если амплитуда колебания маятника близка к , то есть движение маятника на фазовой плоскости близко к сепаратрисе, то под действием малой периодической вынуждающей силы система демонстрирует хаотическое поведение. Это одна из простейших механических систем, в которой хаос возникает под действием периодического возмущения[4].
- Если точка подвеса не неподвижна, а совершает колебания, то у маятника может появиться новое положение равновесия. Если точка подвеса достаточно быстро колеблется вверх-вниз, то маятник приобретает устойчивое положение «вверх тормашками». Такая система называется маятником Капицы.
- В условиях вращения Земли при достаточно длинной нити подвеса плоскость, в которой маятник совершает колебания, будет медленно поворачиваться относительно земной поверхности в сторону, противоположную направлению вращения Земли (маятник Фуко).
Примечания[править | править код]
Ссылки[править | править код]
- Коллекция Java-апплетов, моделирующая поведение математических маятников, в частности маятника Капицы.
- Java-апплет, моделирующий колебание математического маятника при наличии вязкого трения с черчением фазовой траектории.
- Учебный фильм «Математический и физический маятник», производство СССР
См. также[править | править код]
- Физический маятник
- Маятник Фуко
Определение физического и математического маятников
В качестве конкретного примера тела, вращающегося вокруг оси, рассмотрим движение маятников.
Физическим маятником называется твердое тело, обладающее горизонтальной осью вращения, вокруг которой оно совершает колебательные движения под действием своего веса (рис. 119).
Рис. 119
Рис. 120
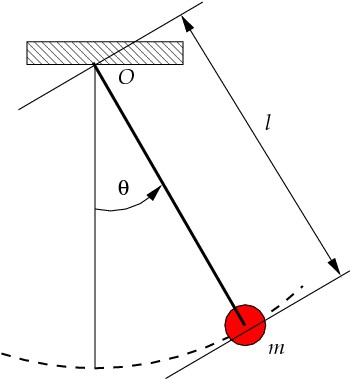
Положение маятника полностью определяется углом его отклонения от положения равновесия, и поэтому для определения закона движения маятника достаточно найти зависимость этого угла от времени.
Уравнение вида:
называется уравнением (законом) движения маятника. Он зависит от начальных условий, т. е. от угла и угловой скорости Таким образом,
Предельным случаем физического Маятника является математический маятник, представляющий (как указывалось ранее — глава 2, § 3) материальную точку, соединенную с горизонтальной осью, вокруг которой она вращается, жестким невесомым стержнем (рис. 120). Расстояние материальной точки от оси вращения называется длиной математического маятника.
Уравнения движения физического и математического маятников
Выберем систему осей координат так, чтобы плоскость ху проходила через центр тяжести тела С и совпадала с плоскостью качания маятника, как это показано на чертеже (рис. 119). Ось направим перпендикулярно к плоскости чертежа на нас. Тогда на основании результатов предыдущего параграфа уравнение движения физического маятника запишем в виде:
где через обозначен момент инерции маятника относительно его оси вращения и
Поэтому можно написать:
Активной силой, действующей на маятник, является его вес момент которого относительно оси привеса будет:
где — расстояние от оси вращения маятника до его центра масс С.
Следовательно, приходим к следующему уравнению движения физического маятника:
Так как математический маятник является частным случаем физического, то записанное выше дифференциальное уравнение справедливо и для математического маятника. Если длина математического маятника равна а вес его то момент инерции его относительно оси вращения равен
Так как расстояние центра тяжести математического маятника от оси равно то окончательно дифференциальное уравнение движения математического маятника можно написать в виде:
Приведенная длина физического маятника
Сравнивая уравнения (16.8) и (16.9), можно заключить, что если параметры физического и математического маятников связаны соотношением
или
то законы движения физического и математического маятников одинаковы (при одинаковых начальных условиях).
Последнее соотношение указывает на ту длину, которую должен иметь математический маятник, чтобы двигаться так же, как соответствующий физический маятник. Эта длина называется приведенной длиной физического маятника. Смысл этого понятия заключается в том, что изучение движения физического маятника можно заменить изучением движения математического маятника, представляющего собой простейшую механическую схему.
Первый интеграл уравнения движения маятника
Уравнения движения физического и математического маятников имеют один и тот же вид, следовательно, уравнение их движения будет
где
Так как единственной силой, которая учитывается в этом уравнении, будет сила тяжести, принадлежащая потенциальному силовому полю, то имеет место закон сохранения механической энергии.
Последний можно получить простым приемом, именно умножим уравнение (16.10) на тогда
или
Интегрируя это уравнение, получим
Определяя постоянную интегрирования Си из начальных условий найдем
Решив последнее уравнение относительно получим
Это соотношение представляет собой первый интеграл дифференциального уравнения (16.10).
Определение опорных реакций физического и математического маятников
Первый интеграл уравнений движения позволяет определить опорные реакции маятников. Как указывалось в предыдущем параграфе, реакции опор определяются из уравнений (16.5). В случае физического маятника составляющие активной силы по осям координат и моменты ее относительно осей будут:
Координаты центра масс определяются формулами:
Тогда уравнения для определения реакций опор принимают вид:
Центробежные моменты инерции тела и расстояния между опорами должны быть известны по условиям задачи. Угловое ускорение в и угловая скорость со определяются из уравнений (16.9) и (16.4) в виде:
где
Таким образом, уравнения (16.12) полностью определяют составляющие опорных реакций физического маятника.
Уравнения (16.12) еще упрощаются, если рассматривать математический маятник. Действительно, так как материальная точка математического маятника расположена в плоскости то Кроме того, так как закреплена одна точка, то Следовательно, уравнения (16.12) обращаются в уравнения вида:
где
Из уравнений (16.13) с использованием уравнения (16.9) следует, что реакция опоры направлена вдоль нити I (рис. 120). Последнее представляет собой очевидный результат. Следовательно, проектируя составляющие равенств (16.13) на направление нити, найдем уравнение для определения реакции опоры вида (рис. 120):
Подставляя сюда значение и учитывая, что запишем:
Последнее соотношение определяет динамическую реакцию математического маятника. Заметим, что статическая реакция его будет
Качественное исследование характера движения маятника
Первый интеграл уравнения движеиия маятника позволяет провести качественное исследование характера движения его. Именно, запишем этот интеграл (16.11) в виде:
В процессе движения подкоренное выражение должно быть либо положительным, либо обращаться в некоторых точках в нуль. Допустим, что начальные условия таковы, что
В этом случае подкоренное выражение нигде не обращается в нуль. Следовательно, при движении маятник будет пробегать все значения угла и угловая скорость со маятника имеет один и тот же знак, который определяется направлением начальной угловой скорости, или угол будет либо все время возрастать, либо все время убывать, т. е. маятник будет вращаться в одну сторону.
Направления движения будут соответствовать тому или иному знаку в выражении (16.11). Необходимым условием реализации такого движения является наличие начальной угловой скорости, так как из неравенства (16.14) видно, что если то ни при каком начальном угле отклонения получить такое движение маятника невозможно.
Пусть теперь начальные условия таковы, что
В этом случае найдутся два таких значения угла при которых подкоренное выражение обращается в нуль. Пусть они соответствуют углам, определяемым равенством
Причем будет где-то в диапазоне изменения от 0 до . Далее, очевидно, что при
подкоренное выражение (16.11) будет положительным и при сколь угодно мало превышающем оно будет отрицательным.
Следовательно, при движении маятника его угол изменяется в диапазоне:
При угловая скорость маятника обращается в нуль и угол начинает уменьшаться до значения . При этом изменится знак угловой скорости или знак перед радикалом в выражении (16.11). Когда достигает значения угловая скорость маятника вновь обращается в нуль и угол опять начинает увеличиваться до значения
Таким образом, маятник будет совершать колебательные движения
Амплитуда колебаний маятника
При колебательных движениях маятника максимальная величина его отклонения от вертикали называется амплитудой колебания. Она равна которое определяется из равенства
Как следует из последней формулы, амплитуда колебания зависит от начальных данных основных характеристик маятника или его приведенной длины.
В частном случае, когда маятник отклонен от равновесного положения и отпущен без начальной скорости то будет равно , следовательно, амплитуда не зависит от приведенной длины.
Уравнение движения маятника в конечной форме
Пусть начальная скорость маятника равна нулю, тогда первый интеграл уравнения движения его будет:
Интегрируя это уравнение, находим
Будем вести отсчет времени от положения маятника, соответствующего тогда
Преобразуем подынтегральное выражение с помощью формулы:
Тогда получим:
Полученный интеграл называется эллиптическим интегралом первого рода. Он не может быть выражен с помощью конечного числа элементарных функций.
Обращение эллиптического интеграла (16.15) относительно его верхнего предела представляет уравнение движения маятника:
Это будет хорошо изученная эллиптическая функция Якоби.
Период колебания маятника
Время одного полного колебания маятника называется периодом его колебания. Обозначим его Т. Так как время движения маятника от положения до положения такое же, как время движения от то Т определится формулой:
Далее, так как при движении от до скорость отрицательна, то перед интегралом следует взять знак минус. Тогда
Сделаем замену переменных, положив
При изменяющихся в пределах от 0 до будет меняться от 0 до . Далее,
и, следовательно,
Последний интеграл называется полным эллиптическим интегралом первого рода (значения его даются специальными таблицами).
При подынтегральная функция стремится к единице и .
Приближенные формулы малых колебаний маятника
В случае когда колебания маятника имеют небольшую амплитуду (практически не должно превышать 20°), можно положить
Тогда дифференциальное уравнение движения маятника преобретает вид:
где приведенная длина маятника.
Это уравнение интегрируется в элементарных функциях. Общее решение его имеет вид:
где А и постоянные, зависящие от начальных условий определяемые из формулы:
или
Уравнение движения маятника в конечной форме (16.17) является периодической функцией от I. Это уравнение описывает колебательное движение с амплитудой А (зависящей от начальных условий) и периодом, который определяется формулой:
Как следует из формулы, период не зависит от начальных условий и определяется только приведенной длиной маятника. Это свойство малых колебаний маятника называется изохронностью. Оно используется, например, в часах, где благодаря изохронности обеспечивается точность хода.
Использование маятников для экспериментального определения ускорения силы тяжести на земной поверхности
Как следует из предыдущего, период колебания маятника зависит от Этим обстоятельством можно воспользоваться для экспериментального определения Обычно для этого применяется при бор, называемый оборотным маятником. Последний состоит из стержня с двумя призмами (рис. 121), ребра которых лежат на одной прямой с центром масс маятника, по обе стороны от него. Ребро может двигаться вдоль . Оборотный маятник может качаться относительно осей, совпадающих с ребрами . Принцип действия этого прибора основывается на следующем свойстве осей качания маятников. Как указывалось, приведенная длина маятника определяется формулой:
Рис. 121
Преобразуем это выражение, используя теорему Гюйгенса — Штейнера. Именно,
где — момент инерции маятника относительно оси, параллель ной оси его качания и проходящей через его центр масс, М — масса маятника. Тогда
Но где — радиус инерции маятника относительно оси, проходящей через центр масс. Следовательно,
Отсюда видно, что приведенная длина маятника всегда больше расстояния от его центра до оси подвеса. Отложим от точки О вдоль линии отрезок и заставим этот маятник качаться около новой оси, параллельной первоначальной, но проходящей через точку О. В этом случае роль отрезка а будет играть отрезок
и приведенная длина V равна:
или
Таким образом, приведенная длина маятника, а следовательно и закон его движения вокруг осей О и О не изменяется. Возвращаясь к оборотному маятнику, заставим его качаться относительно оси, совпадающей с ребром О, а потом — с ребром О. Затем, передвигая призму О вдоль , добьемся такого положения, когда периоды этих колебаний будут одинаковы. Это значит, что
Определив эту длину и измерив амплитуду колебаний и период колебаний Т, обращаясь к формуле (16.16), где найдем:
где
При малых колебаниях формула для определения сильно упрощается и имеет вид:
