Определи по рисункам каким свойством обладают элементы пересечения множеств

Математика часто оперирует абстрактными объектами, для задания связи между которыми существуют различные операции, такие как пересечение и объединение множеств.
Понятие множества является интуитивным, не определяемым. Оно обычно ассоциируется с набором чего-либо, группой каких-то предметов или живых объектов, совокупностью некоторых условий, рассматривается как класс, семейство в некоторой классификации, промежуток числовой прямой. Например, в геометрии рассматриваются линии как множества точек.
То, из чего состоит множество, называется его элементами.
Графическим изображением, служащим для наглядности рассматриваемых объектов, является круг Эйлера.
Что такое пересечение множеств
Для любого набора множеств их пересечением называется множество, состоящее из всех элементов, принадлежащих одновременно каждому из заданных. Другими словами, это совокупность всех общих элементов.
С помощью кругов Эйлера-Венна пересечение можно изобразить так:
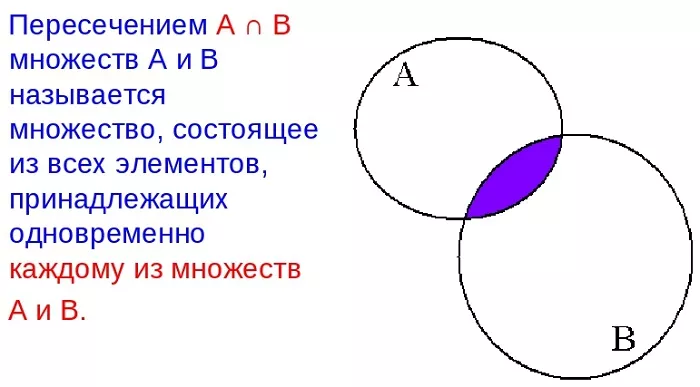
Знак пересечения: ∩.
Часто применяется для определения решений систем уравнений и неравенств.
Ассоциируется с обычным умножением двух числовых объектов.
Что такое объединение множеств
Для любого набора множеств, их объединением называется множество, состоящее из всех элементов, принадлежащих хотя бы одному из заданных.
Изображение кругами Эйлера выглядит следующим образом:
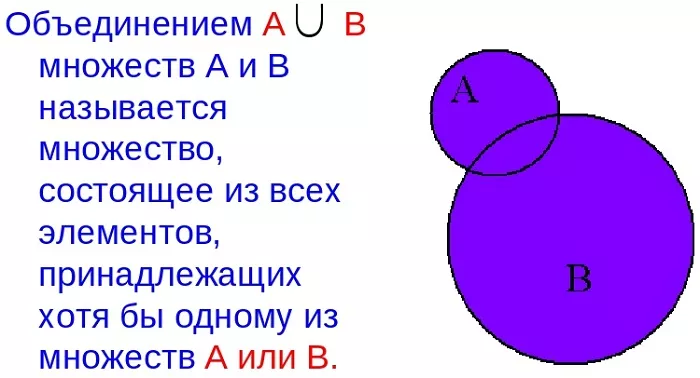
Знак объединения: ∪.
Часто используется при решении уравнений и неравенств, подчёркивая наличие серий корней и решений, нескольких используемых промежутков числовой прямой.
В обычной математике близко по смыслу с операцией, называемой «сложение».
Для решения задач нужно знать о следующих свойствах:
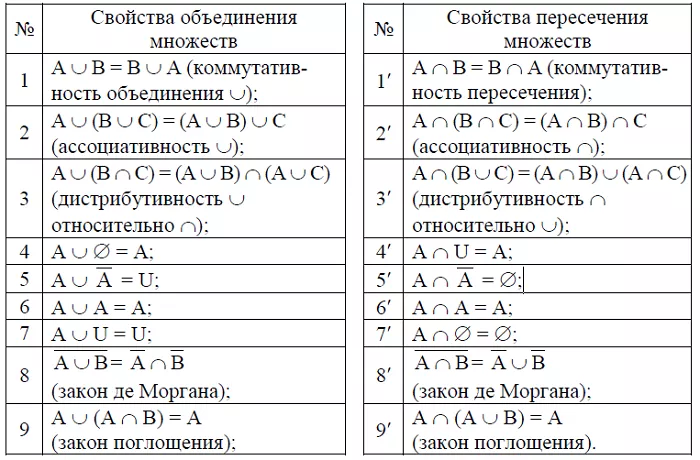
1. Коммутативность (перестановочность):
A ∩ B = B ∩ A;
A ∪ B = B ∪ A.
Эти свойства распространяются на любое количество компонентов. Следуют из определения операций.
2. Ассоциативность (расстановка скобок):
(A ∩ B) ∩ C = A ∩ (B ∩ C);
(A ∪ B) ∪ C = A ∪ (B ∪ C).
Данные свойства также применимы к большому количеству компонентов. Позволяют опускать скобки и упрощать запись.
3. Дистрибутивность (раскрытие скобок):
(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C);
(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C).
4. Закон идемпотентности (идентичности):
A ∩ A = A;
A ∪ A = A.
Множество, не содержащее ни одного элемента, называется пустым. Обозначается перечёркнутым нулём: Ø
Выполнение операций с Ø:
A ∩ Ø = Ø;
A ∪ Ø = Ø.
Прослеживается аналог со сложением и умножением на ноль.
Операции над множествами
Помимо объединения и пересечения существуют другие операции:
Для двух множеств A и B можно определить их разность как набор элементов, входящих в A и не содержащихся в B:
(AB)
Рассматривая некоторое множество в качестве содержащего все остальные, можно прийти к понятию «дополнение», как к совокупности всех элементов, не входящих в A:
Благодаря этой операции свойства объединения и пересечения можно расширить/
Закон де Моргана:
![]()
![]()
Примеры решения задач
Задача №1
B A, B ∪ A.
Пусть
![]()
Выписать все элементы множества
![]()
где
![]()
Решение.
При поиске M операции выполняются последовательно.
B A состоит из всех элементов B, которые не принадлежат A, поэтому:
![]()
B ∪ A включает в себя все элементы, принадлежащие хотя бы одному из множеств A или B. Таким образом:
![]()
M = (B A) (B ∪ A) состоит из всех элементов B A, которые не принадлежат B ∪ A, следовательно, M = Ø.
Задача №2
Доказать методом включений тождество:
![]()
Решение.
Необходимо доказать выполнение включений:
![]()
и
![]()
Шаг 1.
Выбирается произвольный x из (A ∩ B) ∪ C. По определению операции объединения x ∈ B ∩ A или x ∈ C.
Если x ∈ B ∩ A, то по определению пересечения x ∈ B и x ∈ A.
Так как x ∈ A, то x ∈ C ∪ A; так как x ∈ B, то x ∈ C ∪ B, следовательно, x ∈ (A ∪ C) ∩ (B ∪ C).
Если x ∈ C, то x ∈ C ∪ A и x ∈ C ∪ B, а значит: x ∈ (A ∪ C) ∩ (B ∪ C).
Поскольку x ∈ (A ∩ B) ∪ C был выбран произвольно, утверждается, что любой элемент этого множества содержится в (A ∪ C) ∩ (B ∪ C), то есть:
![]()
Шаг 2.
Выбирается произвольный y из (A ∪ C) ∩ (B ∪ C).
По определению операции пересечения y ∈ C ∪ A и y ∈ C ∪ B.
Так как y ∈ C ∪ A, то y ∈ A или y ∈ C; так как y ∈ C ∪ B, то y ∈ C или y ∈ B. Таким образом, y ∈ C или y ∈ A и y ∈ B.
Если y ∈ A и y ∈ B, то y ∈ B ∩ A, а, следовательно, y ∈ (A ∩ B) ∪ C; если y ∈ C, то также y ∈ (A ∩ B) ∪ C.
Поскольку y из (A ∪ C) ∩ (B ∪ C) выбирался произвольно, утверждается, что любой элемент этого множества содержится в (A ∩ B) ∪ C, то есть
![]()
Шаг 3.
Из пунктов 1 и 2 вытекает, что
![]()
Доказано.
1. Коммутативность: А п В = В п А.
Обосновать это свойство очень просто. Любой элемент, принадлежащий общей части множеств А и В, т.е. А п В, принадлежит общей части множеств В и А, т.е. В п А, и наоборот.
2. Ассоциативность: А п (В п С) = (А п В) п С.
Докажем это свойство. Нам нужно доказать, что множество в левой части равенства равно множеству в правой части равенства. По определению равенства множеств нужно показать, что А п (В п С) с (А п В) n С, т.е. любой элемент х, принадлежащий А п (В п С), принадлежит и множеству (А п В) п С, а также, что (А п В) п С с А п (В n С), т.е. любой элемент у, принадлежащий (А п В) n С, принадлежит А п (В п С).
- 1) Пусть х — произвольный элемент из множества А п (В п С), т.е. х е е А п (В n С). По определению пересечения множествхе А ихе В п С, а значит, хе А, ихе В, ихе С, т.е. х принадлежит общей части трех множеств А, В и С. Это значит, что х е А п В ихе С, т.е. х е (Л п В) п С.
- 2) Пусть у — произвольный элемент множества (Ап В) п С, т.е. уе (Ап пВ) пС. По определению пересечения у е АпВ и у е С, т.е. у е А, и у е В, и у е С. Следовательно, у е А и у е (В п С), т.е. у е А п (В п С). Свойство доказано.
Это свойство можно проиллюстрировать с помощью диаграммы Эйлера — Венна (рис. 2.6).

Рис. 2.6. Иллюстрация доказательства свойства ассоциативности
- 3. А п U = A.
- 4. Идемпотентность пересечения А пА = А.
Объединение. Следующая операция над множествами называется объединением.
Определение 2.4. Объединением множеств А и В называется новое множество, которое обозначается А и В и состоит из всех элементов, принадлежащих хотя бы одному из множеств А или В, т.е. ЛиВ = {ххе А или х е В).
Например, если А = {1, 2, 3}, В = {1, 3, 4}, то А и В = {1, 2, 3, А).
Покажем объединение двух множеств на диаграмме Эйлера — Венна (рис. 2.7).

Рис. 2.7. Объединение множеств
п
Объединение п множеств записывают так: УД = Д и А2 и…и Дг
/=1
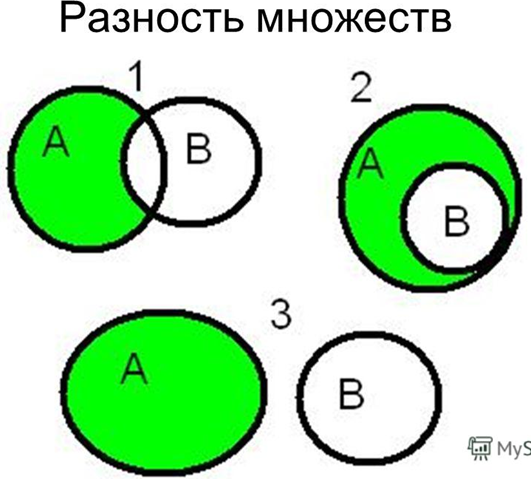
Разность. Кроме операций пересечения и объединения над множествами можно выполнять еще одну операцию — нахождение разности.
Определение 2.5. Разностью множеств А и В называется новое множество, которое обозначается А В и состоит из всех элементов множества Ау не принадлежащих множеству В, т.е. А В = {х х е А и х ? В).
Например, если А = {1, 2, 3}, В = {1, 3, 4}, то А В = {2}.
Па рис. 2.8 показана разность множеств с использованием диаграммы Эйлера — Война.

Рис. 2.8. Разность множеств
Упражнение 2.1
Найдите разность множеств ВА, если А = {1,2,3}, В = {1,3,4}. Равны ли разности
АВиВА?
С разностью связано такое понятие, как дополнение одного множества до другого.
Определение 2.6. Дополнением множества А до множества В, если Лей, называется множество, которое обозначается А(В) и состоит из всех элементов В, не принадлежащих А. Очевидно, что А(В) = В А, при условии что А с В.
Говоря о дополнении множества Л, часто имеют в виду дополнение его до универсального множества, т.е. A(U) = U А. Иногда для обозначения дополнения множества до универсального используют значок А.
Кстати, изображать универсальное множество принято в виде прямоугольника.
Перечисленные выше операции используются при решении задач. Рассмотрим такую задачу.
Пример 2.4
Пусть в студенческой группе, насчитывающей 25 человек, 20 человек занимаются легкой атлетикой, 18 человек — волейболом и нет ни одного человека, кто бы не занимался другим видом спорта или ни одним из видов спорта. Есть ли в этой группе студенты, занимающиеся и легкой атлетикой, и волейболом? Сколько студентов этой группы занимаются только волейболом?
Решение
В данной задаче в качестве универсального множества следует рассматривать множество всех студентов группы (их 25). Кроме того, в него входят два подмножества: множество студентов группы, занимающихся легкой атлетикой (их 20); множество студентов группы, занимающихся волейболом (их 18). Общее количество занимающихся двумя видами спорта — 38 (20 + 18) — больше, чем студентов в группе. Происходит это потому, что студентов, которые занимаются обоими видами спорта, мы учли дважды — они входят и в первое, и во второе подмножества, т.е. в их пересечение. Их количество равно 13 (38 — 25). Из этого следует, что только волейболом занимаются 5(18- 13) студентов группы.
На диаграмме это решение будет выглядеть так (рис. 2.9).
В приведенном примере нас интересовали не только множества и их связи (например, наличие пересечения и объединения множеств), но и количество элементов в них, так как все рассматриваемые множества являются конечными. Количество элементов конечного множества А называют мощностью множества и обозначают т(А)[.
При решении этого примера мы воспользовались принципом включения-исключения, который выражается некоторой формулой. Приведем ее для случая двух конечных множеств Ах и А2:
т(Ах и А2) = т(А{) + т{А2) — т(Ах п А2).
В случае если Ах п А2 — 0, последний член формулы будет равен нулю.
Этот принцип позволяет определить мощность объединения конечного числа конечных множеств, которые могут пересекаться друг с другом.
В общем случае формула включения-исключения выглядит следующим образом:

Пример 2.5

Рис. 2.9. К примеру 2.4
На первом курсе по одной из образовательных программ обучаются 34 студента. Каждый из них пользуется хотя бы одним из видов городского транспорта для поездки к месту учебы: метро, автобусом и троллейбусом. Всеми тремя видами транспорта пользуются 5 студентов, метро и автобусом — 13 студентов, метро и троллейбусом — 14 студентов, троллейбусом и автобусом — 9 студентов. Сколько студентов пользуются только одним видом транспорта?
Решение
Такого вида задачи чаще всего решаются с использованием диаграмм Эйлера — Венна. Обозначим А — рассматриваемое множество студентов, которые добираются до места учебы на метро; В — множество студентов, которые пользуются автобусом; С — множество студентов, пользующихся троллейбусом.
Учитывая условие задачи, их можно изобразить следующим образом.
По условию, объединение этих множеств содержит 34 элемента. В области, где все три множества пересекаются, находятся 5 элементов. В пересечении множеств А и В должно находиться 13 элементов, но 5 из них уже учтены. Это означает, что в области, изображающей множество студентов, которые пользуются только метро и автобусом, находятся 13-5 = 8 элементов. Таким же образом, расставим числовые дан- [1]
ные в те области, где это возможно. Найдем их сумму: 8 + 4 + 5 + 9 = 26. Это число характеризует число студентов, которые пользуются двумя и тремя видами транспорта, чтобы доехать до места учебы.

Рис. 2.10. К примеру 2.5
Незаполненными числами окажутся области, которые изображают множество студентов, пользующихся только одним видом транспорта (либо метро, либо автобусом, либо троллейбусом). Их число равно 34 — 26 = 8. Это и есть ответ задачи.
Объясните, можно ли по данному условию задачи определить, сколько студентов пользуются каждым видом транспорта.
Определение 2.7. Декартовым произведением множеств А и В называется новое множество, обозначаемое Ах В, элементами которого являются всевозможные пары (а, 6), где а е А, b е В, т.е. Ах В = {(а, Ь) а е Л, be В}.
Например, если А = {1, 2, 3}, В = {1, 3, 4}, то Ах В = {(1, 1), (1, 3), (1, 4), (2,1), (2, 3), (2,4), (3,1), (3, 3), (3,4)}.
Декартово произведение множеств является особенной операцией, так как множество, полученное в результате ее выполнения, является частью универсального множества, состоящего не из отдельных элементов, как исходные множества Л и В, а из пар соответствующих элементов.
Кстати, с декартовым произведением связано понятие координатной плоскости. Ведь если рассматривать множество координат точек координатной плоскости, то оно является декартовым произведением R х R, где первое множество действительных чисел R — координаты точек оси X, а второе R — координаты точек оси У.
Множества и его элементы
УРОК 9 РЕШЕНИЕ ЗАДАЧ. Самостоятельная работа.
Цель: Систематизация знаний по теме «Множества и его элементы».
Повторение, проверка д/з:
Что обозначает слово «множество»?
Что мы называем элементом множества?
Что бывает элементами множества?
Как различают множества по числу элементов?
Какими способами можно задать множество? (перечисление элементов, характеристическое свойство)
Какое свойство называется характеристическим свойством?
Какие множества называются равными?
Какие математические «иероглифы» мы используем для сокращенной записи?
Что такое подмножество?
Что такое круги Эйлера? Зачем они? (Круги Эйлера – геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления)
Что такое объединение множеств? Знак объединения.
Что такое пересечение множеств? Знак пересечения. Решить упражнение 1.
Что такое разность множеств? Знак разности. Проверить упражнения 1, 2 из д/з.
Что такое дополнение множества?
Решить упражнение 2, 3, 4.
Проверить упражнения из домашнего задания:
Найти разность множеств: К = {1; 2; 3; 7; 8; 9} и М = {0; 2; 8}. Решение: К М = {1; 3; 7; 9}.
Даны множества: А = {a; b; c; d}, В = {c; d;} .
Найти: а) А В; б) В А; в) (А В) ∪ (В А). Решение: а) А В = {a; b}; б) В А = ; в) (А В) ∪ (В А) = {a; b} ∪ = {a; b}.
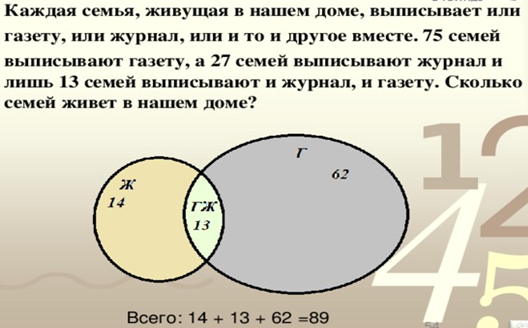
Каждая семья, живущая в нашем доме выписывает или газету, или журнал, или и то и другое вместе. 75 семей выписывают газету, а 27 семей выписывают и газету, и журнал. Сколько семей живет в нашем доме?
Решение:

Упражнение 1: Даны два множества А = {2; 4; 6; 8; 10} и В = {3; 6; 9; 12}. Найти объединение и пересечение этих множеств.
Решение: А ∪ В = {2; 4; 6; 8; 10; 3; 6; 9; 12}, А ∩ В = {6}.
Упражнение 2: Даны два множества Х = {0; 1; 3; 5} и У = {1; 2; 3; 4}. Найти разность множеств Х и У и разность множеств У и Х. Сделайте вывод.
Решение: Х Y = {0, 1, 3, 5} {1, 2, 3, 4} = {0, 5}. Y X = {2; 4}.
Упражнение 3: Объяснить рисунки:

Упражнение 4: Какое число является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Решение: Нуль является дополнением множества натуральных чисел относительно множества неотрицательных целых чисел.
Самостоятельная работа (с последующей взаимопроверкой и проверкой)
Вариант 1
№1 Записать множество А натуральных делителей числа 12.
№2 В данном множестве В = {лев, лисица, гиена, слон, рысь} все элементы, кроме одного, обладают некоторым свойством. Запишите это характеристическое свойство и найдите элемент, не обладающий им.
№3 Даны множества: А = {1, 2, 3, 4, 5, 6} и В = {3, 4, 5, 6, 7, 8}. Найти объединение, пересечение и разность этих множеств.
Вариант 2
№1 Записать множество А натуральных делителей числа 18.
№2 В данном множестве С = {яблоко, груша, огурец, слива, абрикос} все элементы, кроме одного, обладают некоторым свойством. Запишите это характеристическое свойство и найдите элемент, не обладающий им.
№3 Даны множества: А = {3, 4, 5, 6, 7, 8} и В = {4, 5, 6, 7, 8, 9, 10}. Найти объединение, пересечение и разность этих множеств.
Взаимопроверка, проверка.
РЕШЕНИЕ:
Вариант 1:
№1 А = {1, 2, 3, 4, 6, 12}
№2 В = {х│х — хищники}, слон – лишний элемент
№3 А ∪ В = {1, 2, 3, 4, 5, 6, 7, 8}; А ∩ В = {3, 4, 5, 6}; А В = {1, 2}.
Вариант 2:
№1 А = {1, 2, 3, 6, 9, 18}
№2 В = {х│х — фрукты}, огурец – лишний элемент
№3 А ∪ В = {3, 4, 5, 6, 7, 8, 9, 10}; А ∩ В = {4, 5, 6, 7, 8}; А В = {3}
РЕШЕНИЕ ЗАДАЧ
Проверить упражнение 3 из д/з (все предложенные детьми варианты решений).
Дома вы решаете задачи №3 разными способами. Сегодня на уроке мы разберем их решение, используя круги Эйлера.
Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи.
Напомню: круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления.
Упражнение 4: Составьте рассказ по рисунку:
Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче.
Решим простую задачу, применив круги Эйлера:
Задача 1: В детском саду 52 ребенка. Каждый из них любит пирожное или мороженое. Половина детей любит пирожное, а 20 человек – пирожное и мороженое. Сколько детей любит только мороженое?
Аналогичным способом можно решить и домашнее упражнение 3. Давайте попытаемся это сделать!
Рассмотрим решение методом кругов Эйлера задач из прошлых д/з:
Задача: Каждый учащийся в классе изучает английский или французский язык. Английский язык изучают 25 учащихся, французский — 27 учащихся, а два языка — 18 учащихся. Сколько учащихся в классе?
Решение:

Задача: Из 220 школьников 16 играют в баскетбол, 175 в футбол, 24 не играют в эти игры. Сколько человек одновременно играют в баскетбол и в футбол?
Решение:

И новые задачи:
Задача 2: В классе 30 учащихся. Из них 18 человек занимаются в секции легкой атлетики, 10 – плаванием, 3 человека – и тем и другим. Сколько человек не занимается ничем?
Решение:

Задача 2: Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах?
Решение:

Всеми тремя спортивными снарядами владеют три человека, значит, в общей части кругов вписываем число 3. На скейтборде и на роликах умеют кататься 10 человек, а 3 из них катаются еще и на сноуборде. Следовательно, кататься только на скейтборде и на роликах умеют 10-3=7 ребят. Аналогично получаем, что только на скейтборде и на сноуборде умеют кататься 8-3=5 ребят, а только на сноуборде и на роликах 5-3=2 человека. Внесем эти данные в соответствующие части. Определим теперь, сколько человек умеют кататься только на одном спортивном снаряде. Кататься на сноуборде умеют 30 человек, но 5+3+2=10 из них владеют и другими снарядами, следовательно, только на сноуборде умеют кататься 20 ребят. Аналогично получаем, что только на скейтборде умеют кататься 13 ребят, а только на роликах – 30 ребят. По условию задачи всего 100 ребят. 20+13+30+5+7+2+3=80 – ребят умеют кататься хотя бы на одном спортивном снаряде. Следовательно, 20 человек не умеют кататься ни на одном спортивном снаряде.
Ответ: 20 человек не умеют кататься ни на одном спортивном снаряде.
Подведение итогов урока, рефлексия
Мне больше всего удалось…
Для меня было открытием то, что …
За что ты можешь себя похвалить?
Что на ваш взгляд не удалось? Почему? Что учесть на будущее?
Мои достижения на уроке.
Домашнее задание: упражнения:
Найти объединение, пересечение и разность множеств А и В, если А = {1; 2; 3; 4; 5; 6} и В = {2; 4; 6; 8; 10; 12}.
Решение: А ∪ В = {1; 3; 4; 5; 6; 8; 10; 12}, А ∩ В = {2; 4; 6}, А В = {1; 3; 5}.
Даны множества: А – множество всех натуральных чисел, кратных 10 и В = {1; 2; 3; … 41}. Найти: А ∩ В.
Из 52 школьников 23 собирают значки, 35 собирают марки, а 16 – и значки, и марки. Остальные не увлекаются коллекционированием. Сколько школьников не увлекабтся коллекционированием?
