Назовите свойства равнобедренного треугольника какие из них
Содержание:
- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
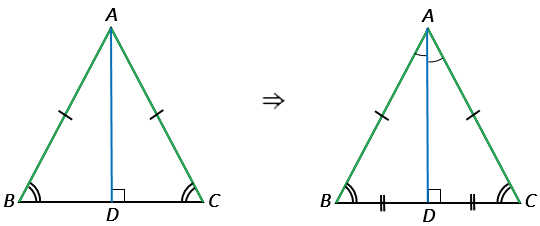
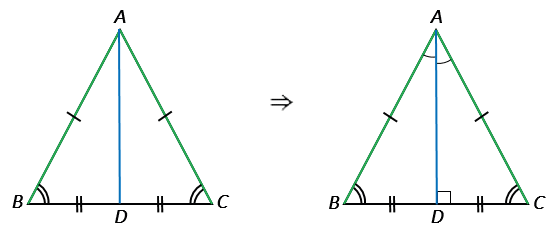
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
- Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок — BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a sin( beta /2)= a sqrt { 2-2 cos beta }
- b = 2a cos alpha
Формулы длины равных сторон — (а):
- a=frac { b } { 2 sin(beta /2) } = frac { b } { sqrt { 2-2 cos beta } }
- a=frac { b } { 2 cosalpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = frac { b } { 2 } *tgalpha
- L = a sqrt { (1 + cos beta)/2 } =a cos (beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
- L = sqrt { a^ { 2 } -b^ { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=frac { 1 } { 2 } *bh
Смотри также:
- Теорема о сумме углов треугольника
- Формулы площади поверхности, основания, сечения призмы
- Площадь поверхности куба, формулы и примеры
- Основные формулы по математике
- Справочные материалы ЕГЭ от ФИПИ по математике
Равнобедренный треугольник, свойства, признаки и формулы
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Равнобедренный треугольник (понятие)
Свойства равнобедренного треугольника
Признаки равнобедренного треугольника
Формулы равнобедренного треугольника
Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник
Равнобедренный треугольник (понятие):
Равнобедренный треугольник – это треугольник, у которого две стороны равны между собой по длине.
Две равные стороны равнобедренного треугольника называются боковыми, а третья неравная им сторона – основанием.
Рис. 1. Равнобедренный треугольник
АВ = ВС – боковые стороны, АС – основание,
∠ АВС – вершинный угол, ∠ BАC и ∠ BСA – углы при основании
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним).
Угол, образованный боковыми сторонами, называется вершинным углом, а углы, одной из сторон которых является основание, называются углами при основании.
Различают следующие виды равнобедренных треугольников:
– остроугольный – все углы острые;
– прямоугольный – угол при вершине прямой, а при основании углы острые;
– тупоугольный – угол при вершине тупой, а при основании углы острые;
– равносторонний (или правильный) – все стороны равны и все углы равны.
Свойства равнобедренного треугольника:
1. В равнобедренном треугольнике углы при основании равны.
Рис. 2. Равнобедренный треугольник
∠ BАC = ∠ BСA
2. Биссектрисы, медианы и высоты, проведённые из этих углов равны между собой.
Рис. 3. Равнобедренный треугольник
АН1 = СН2 – высота, АМ1 = СМ2 – медиана, АL1 = СL2 – биссектриса, проведённые из углов при основании
3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Рис. 4. Равнобедренный треугольник
ВD – биссектриса, высота и медиана, проведенные к основанию – это один и тот же отрезок
4. Центры вписанной и описанной окружностей лежат на медиане (биссектрисе, высоте), проведенной к основанию равнобедренного треугольника.
Рис. 5. Равнобедренный треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
Признаки равнобедренного треугольника:
– если в треугольнике два угла равны, то он равнобедренный;
– если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
– если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
– если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
Формулы равнобедренного треугольника:
Пусть a – длина двух равных сторон равнобедренного треугольника, b – длина основания, h – высота (биссектриса, медиана) равнобедренного треугольника, проведенная к основанию, α – углы при основании, β – вершинный угол, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6, 7, 8).
Рис. 6. Равнобедренный треугольник
Формулы длины основания (b):
,
,
.
Формулы длины равных сторон (а):
.
Формулы углов:
Рис. 7. Равнобедренный треугольник
,
,
.
Формулы периметра (Р) равнобедренного треугольника:
Рис. 8. Равнобедренный треугольник
,
.
Формулы площади (S) равнобедренного треугольника:
,
,
.
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности
2 460
Понятие равнобедренного треугольника
Введем для начала определение треугольника.
Выберем на плоскости три произвольные точки, которые будут удовлетворять условию аксиомы 1. Соединим эти точки между собой отрезками. Тогда
Определение 1
Треугольником будем называть такую геометрическую фигуру, которая состоит из трех точек, не имеющих общей прямой, соединенных отрезками.
Определение 2
Точки в рамках определения 1 называются вершинами треугольника.
Определение 3
Отрезки в рамках определения 1 называются сторонами треугольника.
Введем теперь понятие равнобедренного треугольника.
Определение 4
Треугольник будем называть равнобедренным, если две его стороны будут равны между собой.
Определение 5
Равные стороны в рамках определения 4, будем называть боковыми, а третью – основанием (рис. 1).
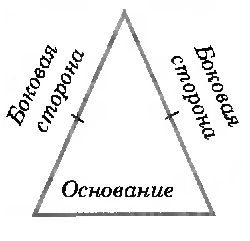
Замечание 1
Отметим, что если боковые стороны равнобедренного треугольника также равняются его основанию, то треугольник будем называть равносторонним.
Свойства равнобедренного треугольника
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Введем свойства равнобедренного треугольника в виде теорем.
Теорема 1
Углы при основании равнобедренного треугольника будут равными.
Доказательство.
Пусть нам дан треугольник $ABC$, в котором $AB=AC$. Проведем биссектрису $AD$ к основанию данного нам треугольника (рис. 2).
Так как $AD$ – биссектриса, то будет верно равенство
$∠1=∠2$
Для треугольников $ABD$ и $ACD$ сторона $AD$ является общей. Следовательно, треугольники $ABD$ и $ACD$ равны по первому признаку. Но тогда будет верно, что
$∠B=∠C$
Теорема доказана.
Замечание 2
Из этой теоремы можно выделить признак равнобедренности треугольника. Если в треугольнике будут иметься два равных угла, то он будет являться равнобедренным.
Теорема 2
Высота, медиана и биссектриса в равнобедренном треугольнике являются одной и той же прямой.
Доказательство.
Пусть нам дан треугольник $ABC$, в котором $AB=AC$. Проведем биссектрису $AD$ к основанию данного нам треугольника (рис. 3). Докажем, для начала, что $AD$ является медианой.
Так как $AD$ – биссектриса, то будет верно равенство
$∠1=∠2$
Для треугольников $ABD$ и $ACD$ сторона $AD$ является общей. Следовательно, треугольники $ABD$ и $ACD$ равны по первому признаку. Но тогда верно, что $BD=DC$. Следовательно, $AD$ – медиана.
Докажем теперь, что $AD$ — высота. Введем следующие обозначения. Пусть $∠1=α$, $∠B=β$.
Так как $AD$ – биссектриса, то $∠A=2α$.
По теореме о сумме углов в треугольнике, из треугольника $ABC$ будем иметь
$∠A+∠B+∠C=180^0$
То есть
$2α+2β=180^0$
$α+β=90^0$
Из треугольника $ABD$ будем иметь
$∠BDA+α+β=180^0$
Тогда
$∠BDA=180^0-(α+β)=180^0-90^0=90^0$
Следовательно, $AD$ — высота.
Теорема доказана.
Пример задач
Пример 1
Пусть дан треугольник $ABC$. Доказать, что если в нем $BD$ будет и высотой и медианой, то треугольник является равнобедренным.
Доказательство.
Для этого нам нужно доказать, что $AB=BC$.
Изобразим рисунок по условию задачи (рис. 4).
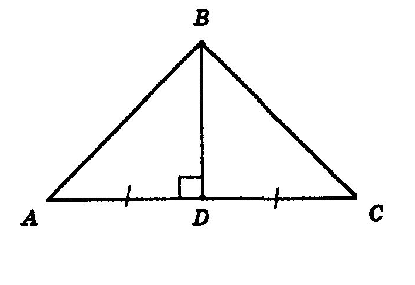
Так как $BD$ является медианой, то по определению 4 будет верно равенство
$AD=DC$
Так как $BD$ является высотой, то по определению 6 будет верно равенство
$∠ADB=∠BDC=90^0$
У треугольников $ADB$ и $BDC$ сторона $BD$ будет общей, следовательно, по всему сказанному выше эти треугольники равняются по первому признаку. Но тогда и стороны $AB$ и $BC$ равны.
Пример 2
Пусть дан треугольник $ABC$. Доказать, что он будет равнобедренным в условиях рисунка 5.
Доказательство.
По условию задачи угол 1 равняется углу 2, а сторона $BD$ равняется стороне $CD$. Так как у треугольников $ADB$ и $ADC$ сторона $AD$ является общей, то треугольники $ADB$ и $ADC$ будут равняться по первому признаку. Но тогда и стороны $AB$ и $AC$ также равны между собой. Следовательно, данный треугольник будет равнобедренным.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Свойства равнобедренного треугольника
1. Теорема
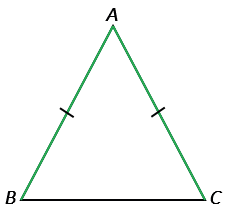
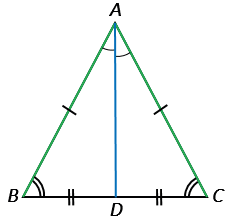
Дано: 
АВС — равнобедренный, ВС — основание.
Доказать: 
В = С.
Доказательство:
Проведем биссектрису АD из вершины А к стороне ВС.
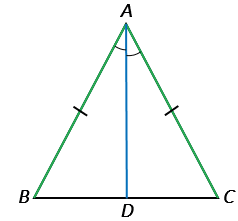
Рассмотрим АВD и АСD: АВ = АС по условию (АВС — равнобедренный), АD — общая сторона, BAD = CAD, так как АD — биссектриса по построению, 
АВD = АСD по первому признаку равенства треугольников В = С,потому что в равных треугольниках против равных сторон лежат равные углы (В лежит против стороны АС, С. — против стороны АВ).
Теорема доказана.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике два угла равны, то такой треугольник равнобедренный.
2. Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
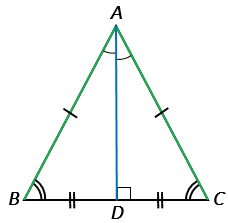
Дано: АВС — равнобедренный, ВС — основание, АD — биссектриса.
Доказать: АD — медиана и высота.
Доказательство:
Рассмотрим АВD и АСD: АВ = АС по условию (АВС — равнобедренный), АD — общая сторона, BAD = CAD, так как АD — биссектриса по условию, АВD = АСD по первому признаку равенства треугольников ВD = DC и ADВ = ADС.
Мы доказали, что ВD = DC точка D — середина стороны ВС, тогда АD является медианой АВС (по определению медианы).
Мы доказали, что ADВ = ADС, причем ADВ и ADС — смежные углы, поэтому ADВ + ADС = 1800, тогда ADВ = ADС =900, т.е. АD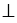
BC, а это означает, что AD является высотой АВС (по определению высоты).
Теорема доказана.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике медиана и высота совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.
3. Теорема
В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике медиана и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.
4. Теорема
В равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике высота и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.
Важно помнить, что данные теоремы справедливы только в том случае, если высота, медиана и биссектриса равнобедренного треугольника проведены к его ОСНОВАНИЮ.
Если треугольник равносторонний, то данные теоремы справедливы для медиан, биссектрис и высот, проведенных к каждой из сторон треугольника.
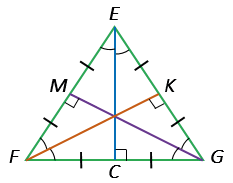
EFG — равносторонний:
- ЕС — биссектриса, медиана и высота, проведенная к стороне FG,
- FK — биссектриса, медиана и высота, проведенная к стороне ЕG,
- GM — биссектриса, медиана и высота, проведенная к стороне ЕF.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 9,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 16,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 490,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 733,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 824,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 828,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 861,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 862,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 910,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Свойства равнобедренного треугольника выражают следующие теоремы.
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Докажем одну из них, например теорему 2.5.
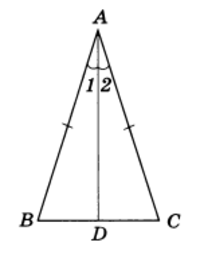
Рис.1
Доказательство. Рассмотрим равнобедренный треугольник ABC с основанием ВС и докажем, что ∠ В = ∠ С. Пусть AD — биссектриса треугольника ABC (рис.1). Треугольники ABD и ACD равны по первому признаку равенства треугольников (АВ = АС по условию, AD — общая сторона, ∠ 1 = ∠ 2, так как AD — биссектриса). Из равенства этих треугольников следует, что ∠ В = ∠ С. Теорема доказана.
С использованием теоремы 1 устанавливается следующая теорема.
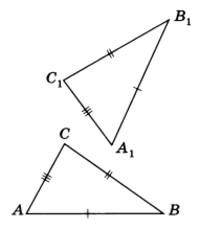
Рис.2
Теорема 5. Третий признак равенства треугольников. Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны (рис. 2).
Замечание. Предложения, установленные в примерах 1 и 2, выражают свойства серединного перпендикуляра к отрезку. Из этих предложений следует, что серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.
Пример 1. Доказать, что точка плоскости, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Решение. Пусть точка М равноудалена от концов отрезка АВ (рис. 3), т. е. AM = ВМ.
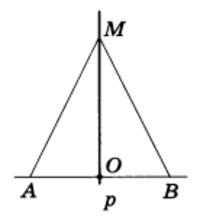
Рис.3
Тогда Δ АМВ равнобедренный. Проведем через точку М и середину О отрезка АВ прямую р. Отрезок МО по построению есть медиана равнобедренного треугольника АМВ, а следовательно (теорема 3), и высота, т. е. прямая МО, есть серединный перпендикуляр к отрезку АВ.
Пример 2. Доказать, что каждая точка серединного перпендикуляра к отрезку равноудалена от его концов.
Решение. Пусть р — серединный перпендикуляр к отрезку АВ и точка О — середина отрезка АВ (см. рис. 3).
Рис.3
Рассмотрим произвольную точку М, лежащую на прямой р. Проведем отрезки AM и ВМ. Треугольники АОМ и ВОМ равны, так как у них углы при вершине О прямые, катет ОМ общий, а катет ОА равен катету ОВ по условию. Из равенства треугольников АОМ и ВОМ следует, что AM = ВМ.
Пример 3. В треугольнике ABC (см. рис. 4) АВ = 10 см, ВС = 9 см, АС = 7 см; в треугольнике DEF DE = 7 см, EF = 10 см, FD = 9 см.
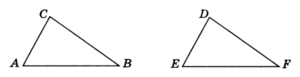
Рис.4
Сравнить треугольники ABC и DEF. Найти соответственно равные углы.
Решение. Данные треугольники равны по третьему признаку. Соответственно равные углы: А и Е (лежат против равных сторон ВС и FD), В и F (лежат против равных сторон АС и DE), С и D (лежат против равных сторон АВ и EF).
Пример 4. На рисунке 5 АВ = DC, ВС = AD, ∠B = 100°.
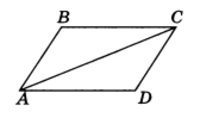
Рис.5
Найти угол D.
Решение. Рассмотрим треугольники ABC и ADC. Они равны по третьему признаку (АВ = DC, ВС = AD по условию и сторона АС — общая). Из равенства этих треугольников следует, что ∠ В = ∠ D, но угол В равен 100°, значит, и угол D равен 100°.
Пример 5. В равнобедренном треугольнике ABC с основанием AC внешний угол при вершине C равен 123°. Найдите величину угла ABC . Ответ дайте в градусах.
Видео-решение.