На каком математическом свойстве основаны эти равенства

После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.

Что такое числовое равенство

Первый раз мы сталкиваемся с числовыми равенствами еще в начальной школе, когда происходит знакомство с числами и понятием «столько же». Т.е. самые примитивные числовые равенства это: 2=2, 5=5 и т.д. И на том уровне изучения мы называли их просто равенствами, без уточнения «числовые», и закладывали в них количественный или порядковый смысл (который несут натуральные числа). Например, равенство 2=2 будет соответствовать изображению, на котором – два цветка и на каждом сидит по две шмеля. Или, к примеру, две очереди, где вторыми по порядку стоят Вася и Ваня.

По мере появления знаний об арифметических действиях числовые равенства становятся сложнее: 5+7=12; 6-1=5; 2·1=2; 21:7=3 и т.п. Затем начинают встречаться равенства, в записи которых участвуют числовые выражения разного рода. Например, (2+2)+5=2+(5+2); 4·(4−(1+2))+12:4−1=4·1+3−1 и т.п. Дальше мы знакомимся с прочими видами чисел, и числовые равенства приобретают все более и более интересный и разнообразный вид.

Определение 1

Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.

Свойства числовых равенств

Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.

Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу bтолько в тех случаях, когда разность a−b есть нуль. Далее в описании каждого свойства мы проследим эту связь.

Основные свойства числовых равенств

Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:

свойство рефлексивности: a=a;
свойство симметричности: если a=b, то b=a;
свойство транзитивности: если a=b и b=c, то a=c,где a, b и c – произвольные числа.

Определение 2

Свойство рефлексивности обозначает факт равенства числа самому себе: к примеру, 6=6, −3=−3, 437=437 и т.п.

Доказательство 1

Нетрудно продемонстрировать справедливость равенства a−a=0для любого числа a: разность a−a можно записать как сумму a+(−a), а свойство сложения чисел дает нам возможность утверждать, что любому числу a соответствует единственное противоположное число −a, и сумма их есть нуль.

Определение 3

Согласно свойству симметричности числовых равенств: если число a равно числу b,
то число b равно числу a. К примеру, 43=64, тогда 64=43.

Доказательство 2

Обосновать данное свойство можно через разность чисел. Условию a=b соответствует равенство a−b=0. Докажем, что b−a=0.

Запишем разность b−aв виде −(a−b), опираясь на правило раскрытия скобок, перед которыми стоит знак минус. Новая запись выражения равна -0, а число, противоположное нулю, это нуль. Таким образом, b−a=0, следовательно: b=a.

Определение 4

Свойство транзитивности числовых равенств гласит, что два числа равны друг другу в случае их одновременного равенства третьему числу. К примеру, если 81=9 и 9=32, то 81=32.

Свойству транзитивности также отвечает определение равных чисел через разность и свойства действий с числами. Равенствам a=b и b=c соответствуют равенства a−b=0 и b−c=0.

Доказательство 3

Докажем справедливость равенства a−c=0, из чего последует равенство чисел a и c. Посколькусложение числа с нулем не меняет само число, то a−c запишем в виде a+0−c. Вместо нуля подставим сумму противоположных чисел −b и b, тогда крайнее выражение станет таким: a+(−b+b)−c. Выполним группировку слагаемых: (a−b)+(b−c). Разности в скобках равны нулю, тогда и сумма (a−b)+(b−c) есть нуль. Это доказывает, что, когда a−b=0 и b−c=0, верно равенство a−c=0, откуда a=c.

Прочие важные свойства числовых равенств

Основные свойства числовых равенств, рассмотренные выше, являются базисом для ряда дополнительных свойств, довольно ценных в разрезе практики. Перечислим их:

Определение 5

Прибавив к (или убавив от) обеим частям числового равенства, являющегося верным, одно и то же число, получим верное числовое равенство. Запишем буквенно: если a=b, где a и b – некоторые числа, то a+c=b+c при любом c.

Доказательство 4

В качестве обоснования запишем разность (a+c)−(b+c).
Это выражение легко преобразуется в вид (a−b)+(c−c).
Из a=b по условию следует, что a−b=0 и c−c=0, тогда (a−b)+(c−c)=0+0=0. Это доказывает, что (a+c)−(b+c)=0, следовательно, a+c=b+c;

Определение 6

Если обе части верного числового равенства перемножить с любым числом или разделить на число, не равное нулю, тогда получим верное числовое равенство.
Запишем буквенно: когда a=b, то a·c=b·c при любом числе c. Если c≠0, тогда и a:c=b:c.

Доказательство 5

Равенство верно: a·c−b·c=(a−b)·c=0·c=0, и из него следует равенство произведений a·c и b·c. А деление на отличное от нуля число c возможно записать как умножение на обратное число 1c;

Определение 7

При a и b, отличных от нуля и равных между собой, обратные им числа также равны.
Запишем: когда a≠0, b≠0 и a=b, то 1a=1b. Крайнее равенство нетрудно доказать: с этой целью разделим обе части равенства a=b на число, равное произведению a·b и не равное нулю.

Укажем еще на пару свойств, которые позволяют осуществлять сложение и умножение соответствующих частей верных числовых равенств:

Определение 8

При почленном сложении верных числовых равенств получается верное равенство. Запись этого свойства такова: если a=b и c=d, то a+c=b+d для любых чисел a, b, c и d.

Доказательство 6

Обосновать это полезное свойство возможно, опираясь на указанные ранее свойства. Мы знаем, что к обеим частям верного равенства возможно прибавить любое число.
К равенству a=bприбавим число c, а к равенству c=d — число b, итогом станут верные числовые равенства: a+c=b+c и c+b=d+b. Крайнее запишем в виде: b+c=b+d. Из равенств a+c=b+c и b+c=b+d согласно свойству транзитивности следует равенство a+c=b+d. Что и нужно было доказать.

Необходимо уточнить, что почленно можно сложить не только два верных числовых равенства, но и три, и более;

Определение 7

Наконец, опишем такое свойство: почленное перемножение двух верных числовых равенств дает верное равенство. Запишем при помощи букв: если a=b и c=d, то a·c=b·d.

Доказательство 7

Доказательство этого свойства подобно доказательству предыдущего. Умножим обе части равенства на любое число, умножим a=b на c, а c=d на b, получим верные числовые равенства a·c=b·c и c·b=d·b. Крайнее запишем как b·c=b·d. Свойство транзитивности дает возможность из равенства a·c=b·c и b·c=b·d вывести равенство a·c=b·d, которое нам необходимо было доказать.

И вновь уточним, что данное свойство применимо для двух, трех и более числовых равенств.
Так, можно записать: если a=b, то an=bn для любых чисел a и b, и любого натурального числа n.

Завершим данную статью, собрав для наглядности все рассмотренные свойства:

a=a.

Если a=b, то b=a.

Если a=bи b=c, то a=c.

Если a=b, то a+c=b+c.

Если a=b, то a·c=b·c.

Если a=bи с≠0, то a:c=b:c.

Если a=b, a=b, a≠0 и b≠0, то 1a=1b.

Если a=b и c=d, то a·c=b·d.

Если a=b, то an=bn.

Источник

В математике , равенство является соотношение между двумя величинами или, в более общем плане двух математических выражений , утверждать , что величины имеют то же значение, или что выражения представляют собой один и тот же математический объект . Равенство между A и B записывается A = B , и выраженный равен B . Символ « = » называется « знак равенства ». Например:

означает , что х и у обозначают один и тот же объект.
означает , что, если х представляет собой любое число, два выражения имеют одинаковое значение. Это также может быть истолковано, говоря , что обе стороны знака равенства представляют ту же функцию .
тогда и только тогда , когда это утверждение, в котором используется установленным строитель обозначений , означает , что, если элементы , удовлетворяющие свойство таких же , как элементы , удовлетворяющих затем два использования множества-строитель обозначения определяет один и тот же набор. Это свойство часто выражается как «два наборов , которые имеют одни и те же элементы равны.» Это одна из обычных аксиом теории множеств , называемых Аксиома объемности .

Этимология

Этимология этого слова от латинского aequālis ( «равно», «как», «сопоставимы», «подобный») от aequus ( «равно», «уровень», «справедливый», «просто»).

Основные свойства

Замена свойство : для любых величин а и Ь и любого выражения F ( х ), если через = Ь , то F ( ) = F ( б ) (если обе стороны имеют смысл, т.е. имеют хорошо сформированные ).

Некоторые конкретные примеры этого:

Для любых действительных чисел , б и с , если а = Ь , то + с = Ь + с (здесь Р ( х ) является й + C );
Для любых действительных чисел , Ь и с , если а = Ь , то — с = Ь — с (здесь F ( х ) является й — с );
Для любых действительных чисел , Ь и с , если через = Ь , то ас = Ьс (здесь F ( х ) является хс );
Для любых действительных чисел , б и с , если а = Ь и с не равна нулю , то / с = б / с (здесь Р ( х ) является х / с ).

Рефлексивное свойство : для любого количества а , = .

Симметричный свойство : для любых величин а и Ь , если а = Ь , то Ь = .

Переходная свойство : Для любых количествах , б и с , если а = Ь и Ь = гр , то через = с .

Эти три свойства делают равенство отношение эквивалентности . Первоначально они были включены в число аксиом Пеано для натуральных чисел. Несмотря на то, симметричные и переходные свойства часто рассматриваются как фундаментальными, они могут быть выведены из подстановки и рефлексивных свойств.

Равенство в качестве предиката

Когда и В не полностью определены или зависят от некоторых переменных , равенства является предложением , которое может быть верны для некоторых значений и ложно для некоторых других значений. Равенство является бинарное отношение , или, другими словами, два аргумента предикат , который может произвести значение истинности ( ложное или истинное ) от своих аргументов. В компьютерном программировании , его вычисление из двух выражений известно как сравнение .

Тождества

Когда и Б можно рассматривать как функции некоторых переменных, то = B означает , что и Б определяют ту же самую функцию. Такое равенство функций иногда называют личностью . Пример ( х + 1) 2 = х 2 + 2 х + 1. Иногда, но не всегда, тождество записывается с тройника: ( х + 1) 2 ≡ х 2 + 2 х + 1.

уравнения

Уравнение является задача нахождения значений некоторых переменных, называемых неизвестными , для которых указанное равенство верно. Уравнение может также относиться к отношению равенства, которое выполняется только для значений переменных , что один заинтересован в. Так , например, х 2 + у 2 = 1 является уравнением из единичной окружности .

Там нет стандартных обозначений , что отличает уравнение от идентичности или иного использования отношения равенства: читатель должен угадать соответствующую интерпретацию от семантики выражений и контекста. Идентичность утверждается , что верно для всех значений переменных в данной области. «Уравнение» иногда может означать идентичность, но чаще всего это указывает подмножество пространства переменной быть подмножеством , где уравнение верно.

Сравнения

В некоторых случаях можно считать равными два математических объектов, которые только эквивалентны свойствам, которые считаются. В частности , в случае геометрии , это где две геометрические фигуры называются равными , когда один может быть перемещен , чтобы совпасть с другой. Слово конгруэнтность также используются для такого рода равенства.

Примерное равенство

Есть некоторые логические системы , которые не имеют никакого понятия равенства. Это отражает неразрешимость равенства двух действительных чисел , определяемой формулами с участием целых чисел , основные арифметические операции , то логарифм и экспоненциальную функцию . Другими словами, не может существовать какой — либо алгоритм для решения такого равенства.

Бинарное отношение « примерно равно » между действительными числами или другими вещами, даже если более точно определена, не является транзитивным (это может показаться так , на первый взгляд, но многие небольшие различия могут сложить что — то большое). Однако, равенство почти всюду является транзитивным.

Связь с эквивалентности и изоморфизма

Рассматриваемое как отношение, равенство является архетипом более общей концепции отношения эквивалентности на множестве: эти бинарные отношения , которые являются рефлексивными , симметричными и переходным . Тождественное соотношение является отношением эквивалентности. Обратно, пусть R отношение эквивалентности, и обозначим через х R класс эквивалентности х , состоящее из всех элементов г , такие , что х К г . Тогда отношение х R Y эквивалентно с равенством х R = у R . Отсюда следует , что равенство является лучшим отношением эквивалентности на любом множестве S в том смысле , что это отношение , которое имеет наименьшие классы эквивалентности (каждый класс сводится к одному элементу).

В некоторых контекстах, равенство резко отличается от эквивалентности или изоморфизма . Например, можно выделить фракции из рациональных чисел , причем последние классы эквивалентности фракций: фракции и различны в долях ( в виде различных цепочек символов) , но они «представляют собой» один и тот же рациональное число (ту же точку на числовой прямой ). Это различие приводит к понятию множества фактора .

Аналогичным образом, наборы

а также

не равные множества — первый состоит из букв, а второй состоит из чисел — но они оба набора из трех элементов , и , таким образом , изоморфны, а это означает , что существует взаимно однозначное соответствие между ними. Например

Тем не менее, существуют и другие варианты изоморфизма, такие как

и эти множества не могут быть идентифицированы без такого выбора — любое утверждение , которое идентифицирует их «зависит от выбора идентификации». Это различие, между равенством и изоморфизмом , имеет фундаментальное значение в теории категорий и одна мотивации для развития теории категорий.

Логические определения

Лейбниц характеризовал понятие равенства следующим образом :

При любом х и у , х = у тогда и только тогда , для любого предиката Р , Р ( х ) , если и только если Р ( у ).

В этом законе, « Р ( х ) тогда и только тогда , когда Р ( у )» может быть ослаблено до « Р ( х ) , если Р ( у )»; модифицированный закон эквивалентен оригиналу, так как заявление , которое применяется к «любым х и у » применяется так же , как хорошо «любые у и х ».

Вместо того , чтобы рассматривать закон Лейбница как истинное утверждение , которое может быть доказанным от обычных законов логики (включая аксиомы о равенстве , таких как симметрии, рефлексивность и замещение), он также может быть принят в качестве определения равенства. Свойство быть отношение эквивалентности, а также свойства , приведенные ниже, то можно доказать: они становятся теоремы .

Равенство в теории множеств

Равенство множеств аксиоматизирована в теории множеств двумя различными способами, в зависимости от того, аксиомы основаны на языке первого порядка с или без равенства.

Установить равенство, основанное на логике первого порядка с равенством

В логике первого порядка с равенством, аксиомой объемности гласит , что два множества , которые содержат одни и те же элементы имеют тот же набор.

Логика аксиома: х = у ⇒ ∀ г , ( г ∈ х ⇔ г ∈ у )
Логика аксиома: х = у ⇒ ∀ г , ( х ∈ Z ⇔ у ∈ Z )
Теория множеств аксиомы: (∀ г , ( г ∈ х ⇔ г ∈ Y )) ⇒ х = у

Включение половины работы в логике первого порядка можно рассматривать лишь как из соображений удобства, как отмечает Леви.

«Причина , почему мы поднимаем первый порядок исчисление предикатов с равенством является вопросом удобства, этим мы спасем труд определения равенства и доказать все свои свойства, это бремя теперь предполагается логикой.»

Установить равенство, основанное на логике первого порядка без равенства

В логике первого порядка без равенства, два набора определяются равными , если они содержат одни и те же элементы. Тогда аксиома объемности утверждает , что два одинаковых набора содержатся в одних и тех же множеств.

Установить определение теории: « х = у » означает ∀ г , ( г ∈ х ⇔ г ∈ у )
Теория множеств аксиомой: х = у ⇒ ∀ г , ( х ∈ Z ⇔ у ∈ Z )

Смотрите также

Равно знак
Неравенство
Логическое равенство
Экстенсиональность
Теория гомотошш типа

Заметки

внешняя ссылка

Хазевинкель, Михель , изд. (2001) [1994], «Аксиомы равенства» , Энциклопедия математики , Springer Science + Business Media BV / Kluwer Academic Publishers, ISBN 978-1-55608-010-4

Источник

50. Свойства равенств, на которых основывается решение уравнений. Возьмем какое-нибудь уравнение, не очень сложное, например:

7x – 24 = 15 – 3x

или

x/2 – (x – 3)/3 – (x – 5)/6 = 1

Мы видим в каждом уравнении знак равенства: все то, что написано слева от знака равенства, называется левою или первою частью уравнения (в первом уравнении 7x – 24 является левою или первою частью, а во втором x/2 – (x – 3)/3 – (x – 5)/6 есть первая, или левая, часть); все то, что написано справа от знака равенства, называется правою или второю частью уравнения (15 – 3x есть правая часть первого уравнения, 1 является правою, или вторю, частью 2-го уравнения).

Каждая часть любого уравнения выражает собою некоторое число. Числа, выражаемые левою и правою частью уравнения, должны быть равны между собою. Нам ясно: если мы к каждому из этих чисел прибавим по одинаковому числу, либо вычтем из них по одинаковому числу, либо каждое из них умножим на одинаковое число, либо, наконец, разделим на одно и то же число, то результаты этих действий должны также быть равными между собою. Другими словами: если a = b, то a + c = b + c, a – c = b – c, ac = bc и a/c = b/c. По поводу деления следует, однако, иметь в виду, что в арифметике не имеется деления на нуль — мы не умеем, например, число 5 разделить на нуль. Поэтому в равенстве a/c = b/c число c не может быть равным нулю.

Итак:

К обеим частям уравнения можно прибавить или из них вычесть по одинаковому числу.
Обе части уравнения можно умножить или разделить на одно и то же число, исключая случай, когда это число может оказаться равным нулю.

Пользуясь этими свойствами уравнения, мы можем найти удобный способ решать уравнения. Выясним этот случай на примерах.

Пример 1. Пусть надо решить уравнение

5x – 7 = 4x + 15.

Мы видим, что первая часть уравнения содержит два члена; один из них 5x, содержащий неизвестный множитель x, можно назвать неизвестным членом, а другой –7 – известным. Во второй части уравнения также 2 члена: неизвестный 4x и известный +15. Сделаем так, чтобы в левой части уравнения оказались только неизвестные члены (а известный член –7 уничтожился бы), а в правой части оказались бы только известные члены (а неизвестный член +4x уничтожился бы). Для этой цели прибавим к обеим частям уравнения одинаковые числа: 1) прибавим по +7 (чтобы уничтожился член –7) и 2) прибавим по –4x (чтобы уничтожился член +4x). Тогда получим:

5x – 7 + 7 – 4x = 4x + 15 + 7 – 4x

Сделав в каждой части уравнения приведение подобных членов, получим

x = 22.

Это равенство и является решением уравнения, так как оно указывает, что для x надо взять число 22.

Пример 2. Решить уравнение:

8x + 11 = 7 – 4x

Опять прибавим к обеим частям уравнения по –11 и по +4x, получим:

8x + 11 – 11 + 4x = 7 – 4x – 11 + 4x

Выполнив приведение подобных членов, получим:

12x = –4

Разделим теперь обе части уравнения на +12, получим:

x = –4/12 или x = –1/3

(первую часть уравнения 12x разделить на 12 – получим 12x/12 или просто x; вторую часть уравнения –4 разделить на +12 – получим –4/12 или –1/3).

Последнее равенство и является решением уравнения, так как оно указывает, что для x надо взять число –1/3.

Пример 3. Решить уравнением

x – 23 = 3 · (2x – 3)

Раскроем сначала скобки, получим:
x – 23 = 6x – 9

Прибавим к обеим частям уравнения по +23 и по –6x, – получим:

x – 23 + 23 – 6x = 6x – 9 + 23 – 6x.

Теперь, для того, чтобы впоследствии ускорить процесс решения уравнения, не будем сразу выполнять приведение всех подобных членов, а только заметим, что члены –23 и +23 в левой части уравнения взаимно уничтожаются, также члены +6x и –6x в первой части взаимно уничтожаются – получим:

x – 6x = –9 + 23.

Сравним это уравнение с начальным: вначале было уравнение:

x – 23 = 6x – 9

Теперь получили уравнение:

x – 6x = –9 + 23.

Мы видим, что в конце концов оказалось, что член –23, находившийся сначала в левой части уравнения, теперь как бы перешел в правую часть уравнения, причем у него переменился знак (в левой части начального уравнения был член –23, теперь его там нет, но зато в правой части уравнения имеется член + 23, которого там раньше не было). Так же точно в правой части уравнения был член +6x, теперь его там нет, но появился зато в левой части уравнения член –6x, которого раньше там не было. Рассматривая с этой точки зрения примеры 1 и 2, мы придем к общему заключению:

Можно любой член уравнения перенести из одной части в другую, меняя знак у этого члена (в дальнейших примерах мы будем этим пользоваться).

Итак, возвращаясь к нашему примеру, мы получили уравнение

x – 6x = –9 + 23

Выполним приведение подобных членов:

–5x = +14

Разделим обе части уравнения на –5. Тогда получим:

x = –2(4/5)

[–5x : (–5) получим x] – это и есть решение нашего уравнения.

Пример 4. Решить уравнение:

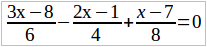
Пример уравнения

Сделаем так, чтобы в уравнении не было дробей. Для этой цели найдем общего знаменателя для наших дробей – общим знаменателем служит число 24 – и умножим на него обе части нашего уравнения (можно, ведь, чтобы равенство не нарушалось, умножить на одно и то же число только обе части уравнения). В первой части 3 члена, причем каждый член является дробью — надо, следовательно, каждую дробь умножить на 24: вторая часть уравнения есть 0, а нуль умножить на 24 — получим нуль. Итак,

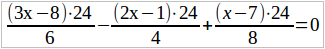
Сокращение знаменателя уравнения

Мы видим, что каждая из наших трех дробей, благодаря тому, что она умножена на общее наименьшее кратное знаменателей этих дробей, сократится и сделается целым выражением, а именно получим:

(3x – 8) · 4 – (2x – 1) · 6 + (x – 7) · 3 = 0

Конечно, желательно все это выполнить в уме: надо вообразить, что, например, числитель первой дроби заключается в скобки и умножается на 24, после чего воображение поможет нам увидеть сокращение это дроби (на 6) и конечный результат, т. е. (3x – 8) · 4. Тоже имеет место и для остальных дробей. Раскроем теперь в полученном уравнении (в его левой части) скобки:

12x – 32 – 12x + 6 + 3x – 21 = 0

(обратим внимание, что здесь понадобилось двучлен 2x – 1 умножить на 6 и полученное произведение 12x – 6 вычесть из предыдущего, благодаря чему знаки членов этого произведения должны перемениться — выше и написано –12x + 6). Перенесем известные члены (т. е. –32, +6 и –21) из левой части уравнения в его правую часть, причем (как мы уже знаем) знаки этих членов должны перемениться — получим:

12x – 12x + 3x = 32 – 6 + 21.

Выполним приведение подобных членов:

3x = 47

(при навыке должно сразу выполняться и перенесение нужных членов из одной части уравнения в другую и приведение подобных членов), разделим, наконец, обе части уравнения на 3 — получим:

x = 15(2/3) — это и есть решение уравнения.

Пример 5. Решить уравнение:

5 – (3x + 1)/7 = x + (2x – 3)/5

Здесь две дроби, и их общий знаменатель равен 35. Умножим, чтобы освободить уравнение от дробей, обе части уравнения на общего знаменателя 35. В каждой части нашего уравнения 2 члена. При умножении каждой части на 35 должно каждый член умножить на 35 — получим:

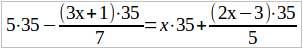
Сокращение знаменателя в уравнении

Дроби сократятся — получим:

175 – (3x + 1) · 5 = 35x + (2x – 3) · 7

(конечно, можно было бы при навыке написать сразу это уравнение).

Выполним все действия:

175 – 15x – 5 = 35x + 14x – 21.

Перенесем все неизвестные члены из правой части (т. е. члены +35x и +14x) в левую, а все известные члены из левой части (т. е. члены +175 и –5) в правую — следует при этом не забывать у переносимых членов менять знак:

–15x – 35x – 14x = –21 – 175 + 5

(член –15x, как раньше был в левой части, так и теперь в ней остался — у него поэтому отнюдь не следует менять знака; аналогичное имеет место и для члена –21). Сделав приведение подобных членов, получим:

–64x = –191.

[Возможно сделать так, чтобы не было знака минус в обеих частях уравнения; для этого умножим обе части уравнения на (–1), получим 64x = 191, но этого можно и не делать.]
Разделим затем обе части уравнения на (–64), получим решение нашего уравнения

x = 2(63/64)

[Если умножили обе части уравнения на (–1) и получили уравнение 64x = 191, то теперь надо обе части уравнения разделить на 64.]

На основании того, что пришлось выполнять в примерах 4 и 5, мы можем установить: можно освободить уравнение от дробей — для этого надо найти общего знаменателя для всех дробей, входящих в уравнение (или наименьшее общее кратное знаменателей всех дробей) и на него умножить обе части уравнения — тогда дроби должны исчезнуть.

Пример 6. Решить уравнение:

5x = 4x.

Перенеся член 4x из правой части уравнения в левую, получим:

5x – 4x = 0 или x = 0.

Итак, решение найдено: для x надо взять число нуль. Если мы заменим в данном уравнении x нулем, получим 5 · 0 = 4 · 0 или 0 = 0, что указывает на выполнение требования, выражаемого данным уравнением: найти такое число для x, чтобы одночлен 5x оказался равен тому же самому числу, как и одночлен 4x.

Если кто-либо подметит с самого начала, что обе части уравнения 5x = 4x можно разделить на x и выполнит это деление, то получится явная несообразность 5 = 4! Причиною этого является то обстоятельство, что деление 5x/x в данном случае выполнить нельзя, так как, мы видели выше, вопрос, выражаемый нашим уравнением, требует, чтобы x = 0, а деление на нуль не выполнимо.

Заметим еще, что и умножение на нуль требует некоторой внимательности: умножая на нуль и два неравных числа, мы получим в результате этих умножений равные произведения, а именно — нули.

Если, например, мы имеем уравнение

x – 3 = 7 – x (его решение: x = 5)

и если кто-либо захочет к нему применить свойство «обе части уравнения можно умножить на одно и тоже число» и умножить обе части на x, то получит:

x2 – 3x = 7x – x2.

После этого может обратить на себя внимание, что все члены уравнения содержат множителя x, из чего можно сделать заключение, что для решения этого уравнения можно взять число нуль, т. е. положить x = 0. И в самом деле, тогда получим:
02 – 3 · 0 = 7 · 0 – 02 или 0 = 0.

Однако, это решение x = 0, очевидно, не годится для данного уравнения x – 3 = 7 – x; заменяя в нем x нулем, получим явную несообразность: 3 = 7!

Источник

На каком математическом свойстве основаны эти равенства

Что такое числовое равенство

Свойства числовых равенств

Основные свойства числовых равенств

Прочие важные свойства числовых равенств

Этимология

Основные свойства

Равенство в качестве предиката

Тождества

уравнения

Сравнения

Примерное равенство

Связь с эквивалентности и изоморфизма

Логические определения

Равенство в теории множеств

Установить равенство, основанное на логике первого порядка с равенством

Установить равенство, основанное на логике первого порядка без равенства

Смотрите также

Заметки

Рекомендации

внешняя ссылка