Какой четырехугольник называется ромбом сформулируйте свойства ромба

У этого термина существуют и другие значения, см. Ромб (значения).
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1].
Этимология[править | править код]
Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.
Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.
Свойства[править | править код]
- Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
- Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
- Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
- Середины четырех сторон ромба являются вершинами прямоугольника.
- Диагонали ромба являются перпендикулярными осями его симметрии.
- В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Признаки[править | править код]
Параллелограмм является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:
- Две его смежные стороны равны (отсюда следует, что все стороны равны, ).
- Его диагонали пересекаются под прямым углом (AC ⊥ BD).
- Одна из диагоналей делит содержащие её углы пополам.
Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].
Квадрат, как частный случай ромба[править | править код]
Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.
Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4].
Уравнение ромба[править | править код]
Уравнение ромба с центром в точке и диагоналями, параллельными осям координат, может быть записано в виде:
где — половины длин диагоналей ромба по осям соответственно.
Длина стороны ромба равна Площадь ромба равна Левый угол ромба рассчитывается по формуле:
Второй угол дополняет его до 180°.
В случае a = b уравнение отображает повёрнутый на 45° квадрат:
где сторона квадрата равна а его диагональ равна Соответственно площадь квадрата равна
Из уравнения видно, что ромб можно рассматривать как суперэллипс степени 1.
Площадь ромба[править | править код]
- Площадь ромба равна половине произведения его диагоналей.
- Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
- Кроме того, площадь ромба может быть вычислена по формуле:
,
где — угол между двумя смежными сторонами ромба.
- Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол :
Радиус вписанной окружности[править | править код]
Радиус вписанной окружности r может быть выражен через диагонали p и q в виде:[5]
В геральдике[править | править код]
Ромб является простой геральдической фигурой.
Червлёный ромб в серебряном поле
В червлёном поле 3 сквозных ромба: 2 и 1
Просверленный червлёный ромб в серебряном поле
В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов
Симметрия[править | править код]
Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.
Ромбический орнамент
Ромбические звёзды
Более сложный орнамент
См. другие примеры на Викискладе.
См. также[править | править код]
- Дельтоид
- Звезда (геометрия)
- Ромбододекаэдр
Примечания[править | править код]
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Четырехугольники
- Ромб и квадрат
Частным видом параллелограмма является ромб.
Ромбом называется параллелограмм, у которого все стороны равны
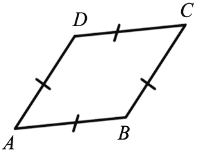
ABCD — ромб.
Ромб обладает всеми свойствами параллелограмма.
Особое свойство ромба
Доказательство
Дано: ABCD — ромб
Доказать: AC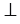 BD,
BD,  ADO =
ADO =  CDO
CDO
Доказательство:
AD = DC (по определению ромба), значит,  ADC — равнобедренный.
ADC — равнобедренный.
AO = OC (по свойству диагоналей параллелограмма),  DO — медиана
DO — медиана  ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,
ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,  AC
AC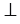 BD,
BD,  ADO =
ADO =  CDO, что и требовалось доказать.
CDO, что и требовалось доказать.
Теорема
Доказательство
Дано: ABCD — параллелограмм, AC BD
BD
Доказать: ABCD — ромб
Доказательство:
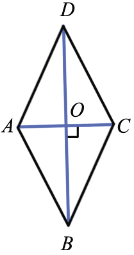
Рассмотрим  AOВ и
AOВ и  COВ:
COВ:
Т.к. AC BD, то
BD, то AOВ =
AOВ =  COВ = 900;
COВ = 900;
AO = OC (по свойству диагоналей параллелограмма), ОВ — общий катет, 
 AOВ =
AOВ =  COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,
COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,  ВС = ВА.
ВС = ВА.
В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD — параллелограмм (по условию) AD = BC =AB = DC (по доказанному).  ABCD — ромб, что и требовалось доказать.
ABCD — ромб, что и требовалось доказать.
Теорема
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб
Доказательство
Дано: ABCD — параллелограмм, АС — диагональ и биссектриса  DAB и
DAB и DCB
DCB
Доказать: ABCD — ромб
Доказательство:
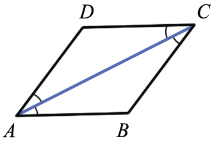
 DAB =
DAB = DCB (по свойству параллелограмма), а АС -биссектриса
DCB (по свойству параллелограмма), а АС -биссектриса  DAB и
DAB и DCB (т.е. АС делит эти углы на два равных угла),
DCB (т.е. АС делит эти углы на два равных угла), 
 DAC =
DAC =  BAC =
BAC = DCA =
DCA =  BCA
BCA
Рассмотрим  ADC:
ADC:  DAC =
DAC = DCA,
DCA, 
 ADC — равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,
ADC — равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD — параллелограмм (по условию) AD = BC =AB = DC (по доказанному).  ABCD — ромб, что и требовалось доказать.
ABCD — ромб, что и требовалось доказать.
Две теоремы, доказанные выше, называют признаками ромба.
Основные свойства квадрата:
1. Все углы квадрата прямые.
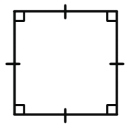
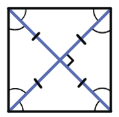
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Многоугольник
Выпуклый многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Трапеция
Прямоугольник
Осевая и центральная симметрии
Четырехугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 16,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 434,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 4,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 500,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 751,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1056,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1072,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1130,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1276,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1290,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
СОДЕРЖАНИЕ СТАТЬИ
1. Параллелограмм
Сложное слово «параллелограмм»? А скрывается за ним очень простая фигура.
Смотри:
 | Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны |
Ну, то есть, взяли две параллельные прямые:

Пересекли ещё двумя:

И вот внутри – параллелограмм!
Какие же есть свойства у параллелограмма?
Свойства параллелограмма.
То есть, чем можно пользоваться, если в задаче дан параллелограмм?
На этот вопрос отвечает следующая теорема:
В любом параллелограмме:
- Противоположные стороны равны
- Противоположные углы равны
- Диагонали делятся пополам точкой пересечения
Давай нарисуем все подробно.
Что означает первый пункт теоремы? А то, что если у тебя ЕСТЬ параллелограмм, то непременно
 | и . |
Второй пункт означает, что если ЕСТЬ параллелограмм, то, опять же, непременно:
 | и |
Ну, и наконец, третий пункт означает, что если у тебя ЕСТЬ параллелограмм, то обязательно:
 | и |
Видишь, какое богатство выбора? Что же использовать в задаче? Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди – какой-нибудь «ключик» да подойдёт.
А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?
На этот вопрос отвечает несколько признаков параллелограмма.
Признаки параллелограмма.
Внимание! Начинаем.
- Признак 1. Если у четырехугольника две стороны равны и параллельны, то это – параллелограмм.
 | ; — параллелограмм. |
— паралелограмм.
- Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 3. Если у четырехугольника противоположные углы равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
Обрати внимание: если ты нашёл хотя бы один признак в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

2. Прямоугольник
Думаю, что для тебя вовсе не явится новостью то, что
 | Прямоугольник – четырехугольник, все углы которого прямые. |
Первый вопрос: а является ли прямоугольник параллелограммом?
Конечно, является! Ведь у него и — помнишь, наш признак 3?
А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма и , а диагонали точкой пересечения делятся пополам.
Но есть у прямоугольника и одно отличительноесвойство.
Свойство прямоугольника
 | Диагонали прямоугольника равны: . |
Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.
 | Если у параллелограмма равны диагонали, то это — прямоугольник. |
Обрати внимание: чтобы стать прямоугольником, четырехугольнику нужно сперва стать параллелограммом, а потом уже предъявлять равенство диагоналей.
3. Ромб
 | Ромб – четырехугольник, все стороны которого равны между собой. |
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него и (вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
- Свойство 1. Диагонали ромба перпендикулярны.
 | (если ты забыл, напомню: — значок перпендикулярности) |
- Свойство 2. Диагонали ромба являются биссектрисами его углов.
Посмотри на картинку:

Как и в случае с прямоугольником, свойства эти – отличительные, то есть по каждому из этих свойств можно заключить, что перед нами не просто параллелограмм, а именно ромб.
Признаки ромба
- Признак 1. Если в параллелограмме диагонали перпендикулярны, то это ромб.

- Признак 2. Если в параллелограммехотя бы одна из диагоналей делит пополам оба угла, через которые она проходит, то этот параллелограмм – ромб.

И снова обрати внимание: должен быть не просто четырехугольник, у которого перпендикулярны диагонали, а именно параллелограмм. Убедись:
 | разве это ромб? |
Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ – биссектриса углов и . Но … диагонали не делятся, точкой пересечения пополам, поэтому – НЕ параллелограмм, а значит, и НЕ ромб.
4. Квадрат
 | Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые. |
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
 | У квадрата угол между диагональю и стороной равен . |
Понятно почему? Квадрат — ромб – биссектриса угла A, который равен . Значит делит (да и тоже) на два угла по .
 | Диагонали квадрата равны, перпендикулярны и делятся точкой пересечения пополам. |
Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще – параллелограмм диагонали делятся точкой пересечения пополам.
 | Если сторона квадрата равна , то его диагональ равна . |
Почему? Ну, просто применим теорему Пифагора к .
Значит, .
СРЕДНИЙ УРОВЕНЬ
Свойства четырехугольников. Параллелограмм
Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.

Свойства параллелограмма
Внимание! Слова «свойства параллелограмма» означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться.
Итак,
Теорема о свойствах параллелограмма.
В любом параллелограмме:
Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.
Итак, почему верно 1)?
 | Давай проведём диагональ . Что получится? Два треугольника: и . |
Раз – параллелограмм, то :
- как накрест лежащие
- как накрест лежащие.
Значит, (по II признаку: и — общая.)
Ну вот, а раз , то и – всё! – доказали.
Но кстати! Мы ещё доказали при этом и 2)!
Почему? Но ведь (смотри на картинку), то есть , а именно потому, что .
Осталось только 3).
Для этого всё-таки придётся провести вторую диагональ.
 | Мы уже выяснили, что . Давай снова отметим равные накрест лежащие углы (посмотри и убедись, что все верно). |
И теперь видим, что — по II признаку ( угла и сторона «между» ними).
 | Значит, (напротив углов и ) и (напротив углов и соответственно). |
Свойства доказали! Перейдём к признакам.
Признаки параллелограмма
Напомним, что признак параллелограмма отвечает на вопрос «как узнать?», что фигура является параллелограммом.
Признак 1. Если у четырехугольника две стороны равны и параллельны, то это параллелограмм.
В значках это так:
 | ; – параллелограмм. |
Почему? Хорошо бы понять, почему – этого хватит. Но смотри:
 | по 1 признаку: , — общая и как накрест лежащие при параллельных и и секущей . |
А раз ,
 | то (лежат напротив и соответственно). Но это значит, что ( и — накрест лежащие и оказались равны). |
Ну вот и разобрались, почему признак 1 верен.
Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | , – параллелограмм. |
Ну, это ещё легче! Снова проведём диагональ .
 | Теперь просто по трём сторонам. |
А значит:
 | и , то есть – параллелограмм. |
Признак 3. Если у четырёхугольника противоположные углы равны, то это – параллелограмм.
 | , – параллелограмм. |
И тоже несложно. Но …по-другому!
 | (ведь – четырехугольник, а , по условию). |
Значит, . Ух! Но и – внутренние односторонние при секущей !
Поэтому тот факт, что означает, что .
А если посмотришь с другой стороны, то и – внутренние односторонние при секущей ! И поэтому .
Видишь, как здорово?!
Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
И опять просто:
 | , как вертикальные , , и . |
Точно так же , , и .
Обрати внимание: если ты нашел хотя бы один признак параллелограмма в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

Свойства четырехугольников. Прямоугольник.
 | Прямоугольник – четырехугольник, все углы которого прямые. |
Свойства прямоугольника:
- Прямоугольник – параллелограмм
- Диагонали прямоугольника равны
Пункт 1) совсем очевидный – ведь просто выполнен признак 3 ( )
А пункт 2) – очень важный. Итак, докажем, что
диагонали прямоугольника равны.
 | Раз прямоугольник – это параллелограмм, то . |
А значит, по двум катетам ( и — общий).
Ну вот, раз треугольники и равны, то у них и гипотенузы и тоже равны.
Доказали, что !
И представь себе, равенство диагоналей – отличительное свойство именно прямоугольника среди всех параллелограммов. То есть верно такое утверждение^
Если у параллелограмма равны диагонали, то это прямоугольник.
Давай поймём, почему?
 | – параллелограмм – по условию. – теперь уже по трём сторонам. |
Значит, (имеются в виду углы параллелограмма). Но ещё раз вспомним, что – параллелограмм, и поэтому .
Значит, . Ну и, конечно, из этого следует, что каждый из них по ! Ведь в сумме-то они должны давать !
Вот и доказали, что если у параллелограмма вдруг (!) окажутся равные диагонали, то это точно прямоугольник.
Но! Обрати внимание! Речь идёт о параллелограммах! Не любой четырехугольник с равными диагоналями – прямоугольник, а только параллелограмм!
Свойства четырехугольников. Ромб
 | Ромб – четырехугольник, все стороны которого равны между собой. |
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него и (Вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
Свойство 1. Диагонали ромба перпендикулярны.
Почему? Ну, раз ромб – это параллелограмм, то его диагонали делятся пополам.
 | Поэтому по трём сторонам ( , — общая, ).И значит, , но они смежные! и . |
Свойство 2. Диагонали ромба являются биссектрисами его углов.
Почему? Да, потому же!
 | Из-за того, что диагонали делятся точкой пересечения пополам, а все стороны ромба равны, весь ромб оказался разделён диагоналями на четыре равных треугольника: . |
Поэтому
Иными словами, диагонали и оказались биссектрисами углов ромба.
Как в случае с прямоугольником, свойства эти – отличительные, каждые из них является ещё и признаком ромба.
Признаки ромба.
Признак 1. Если в параллелограмме диагонали перпендикулярны то это – ромб.
 | — ромб |
Почему? Смотри:
 | — параллелограмм . Но ещё дано, что — по двум катетам. И значит, – и всё! |
Признак 2. Если в параллелограмме хотя бы одна из диагоналей делит пополам оба угла, через которые она проходит, то этот параллелограмм – ромб.
А это почему? А посмотри,
 | , так как – параллелограмм. Но ещё дано, что – биссектриса углов и . |
Значит, и оба этих треугольника – равнобедренные.
 | Значит, , то есть — ромб. |
И снова обрати внимание! Не всякий четырёхугольник с перпендикулярными диагоналями – ромб.
Вот пример:
 | Это вовсе не ромб, хоть его диагонали и перпендикулярны. |
Чтобы быть ромбом, четырёхугольник сперва должен «стать» параллелограммом, а потом уже демонстрировать признак 1 или признак 2.
Свойства четырехугольников. Квадрат
 | Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые. |
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
 | У квадрата угол между диагональю и стороной равен . |
Понятно, почему? Квадрат — ромб – биссектриса угла , который равен . Значит делит (да и тоже) на два угла по .
 | Диагонали квадрата – равны, перпендикулярны и делятся точкой пересечения пополам. |
Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще – параллелограмм диагонали делятся точкой пересечения пополам.
 | Если сторона квадрата равна , то его диагональ равна . |
Почему? Ну, просто применим теорему Пифагора к .
Значит,
КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
 |
|
Свойства параллелограмма:
- Противоположные стороны равны: , .
- Противоположные углы равны: , .
- Углы при одной стороне составляют в сумме : , , , .
- Диагонали делятся точкой пересечения пополам: .
 |
|
Свойства прямоугольника:
- Диагонали прямоугольника равны: .
- Прямоугольник – параллелограмм (для прямоугольника выполняются все свойства параллелограмма).
 |
|
Свойства ромба:
- Диагонали ромба перпендикулярны: .
- Диагонали ромба являются биссектрисами его углов: ; ; ; .
- Ромб – параллелограмм (для ромба выполняются все свойства параллелограмма).
 |
|
Свойства квадрата:
Квадрат — ромб и прямоугольник одновременно, следовательно для квадрата выполняются все свойства прямоугольника и ромба. А так же:
 |
|
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
