Какое свойство алгоритма называется дискретностью

I. Дискретность
Одним из таких свойств является дискретность. Под дискретностью понимается то, что алгоритм состоит из описания последовательности шагов обработки, организованный таким образом, что в начальный момент задаётся исходная ситуация, а после каждого следующего шага ситуация преобразуется на основе данных, полученные в предшествующие шаги обработки. Дискретность алгоритма означает, что он исполняется по шагам: каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
II. Определённость
Другое свойство принято называть определённостью. Оно означает, что на каждом шаге однозначно определено преобразование объектов среды исполнителя, полученных на предшествующих шагах алгоритма.
К примеру, в одном из кулинарных рецептов сказано:
Слегка потрясите, чтобы смесь стала комковатой. Подогрейте коньяк в маленькой кастрюльке и влейте её в смесь.
Формальному исполнителю здесь неясно, требуется ли трясти смесь, пока она вся не станет комом, и какой всё-таки величины кастрюля. Большая или маленькая? И до какой температуры надо подогреть коньяк. Так что такой алгоритм любому исполнителю выполнить довольно трудно, практически невозможно. Можно сказать, что в алгоритме не должны присутствовать не определённые слова: немного, чуть-чуть, слегка и т. д.
III. Результативность
Третье свойство — результативность алгоритма. Это свойство подразумевает, что каждый шаг (и алгоритм в целом) после своего завершения даёт среду, в которой все имеющиеся объекты однозначно определены. Если это по каким — либо причинам невозможно, то алгоритм должен сообщать, что решение задачи не существует.
К примеру, в инструкции по применению лекарства от кашля сказано:
Если врач не прописал, то принимать 3-4 раза в день по 15-20 капель, лучше всего в горячей сладкой воде.
Здесь не определено, например, когда должен заканчиваться алгоритм — когда кашель пройдет или когда лекарство закончиться. Свойство результативности обычно подразумевает конечность алгоритма, т. е. завершение его работы за конечное число шагов (при этом количество шагов может быть заранее не известным и различным для разных исходных данных) .
IV. Понятность
Надо сказать, что алгоритм должен быть понятен не только автору, но и исполнителю. Если мы предложим исполнителю, например утюгу постирать одежду, то он никогда этого не сделает, потому, что не поймет, т. к. такой программы в нём не заложено. Или, например, если мы предложим какому-нибудь мальчику испечь торт то у него, как правило, ни чего не получится, потому что этого они делать не умеют. Но если мы составим подробный алгоритм работы, разобьем его на элементарные шаги, такие, что он без труда поймёт и сможет выполнить каждый шаг, то он сможет успешно испечь любой торт. Каждый шаг алгоритма обязательно представляет собой какое-либо допустимое действие исполнителя. Это свойство алгоритма называют понятностью.
V. Массовость
Наконец, еще одно свойство алгоритма — массовость. Оно означает, что имеется некоторое множество данных, которые могут обрабатываться алгоритмом, или данный алгоритм может быть применен для решения любой задачи одного типа. Массовость алгоритма тесно связанна с понятностью, в качестве примера можно разобрать пример с тортом, и сказать, что чем подробнее будет описан алгоритм приготовления, тем больше вероятности, что торт будет испечен. Также в качестве примера можно взять руководство по эксплуатации электрических приборов, инструкции и т. д. , чем полнее изложен алгоритм работы с приборами, тем легче нам с вами будет в нем разобраться. С точки зрения практической ценность алгоритмов важно, что бы множество допустимых исходных данных было достаточно большим, как правило, практическая ценность алгоритма не велика, если его можно использовать только один раз.
ПОНЯТИЕ АЛГОРИТМА.
СВОЙСТВА АЛГОРИТМА. ВИДЫ АЛГОРИТМОВ. СПОСОБЫ ОПИСАНИЯ АЛГОРИТМОВ
Алгоритмом называется
точное и понятное предписаниe исполнителю совершить последовательность
действий, направленных на решение поставленной задачи. Слово «алгоритм»
происходит от имени математика Аль Хорезми, который сформулировал правила
выполнения арифметических действий. Первоначально под алгоритмом понимали
только правила выполнения четырех арифметических действий над числами.
В дальнейшем это понятие стали использовать вообще для обозначения последовательности
действий, приводящих к решению любой поставленной задачи. Говоря об алгоритме
вычислительного процесса, необходимо понимать, что объектами, к которым
применялся алгоритм, являются данные. Алгоритм решения вычислительной
задачи представляет собой совокупность правил преобразования исходных
данных в результатные.
Основными свойствами
алгоритма являются:
- детерминированность
(определенность). Предполагает получение однозначного результата вычислительного
процecca при заданных исходных данных. Благодаря этому свойству процесс
выполнения алгоритма носит механический характер; - результативность.
Указывает на наличие таких исходных данных, для которых реализуемый
по заданному алгоритму вычислительный процесс должен через конечное
число шагов остановиться и выдать искомый результат; - массовость. Это
свойство предполагает, что алгоритм должен быть пригоден для решения
всех задач данного типа; - дискретность.
Означает расчлененность определяемого алгоритмом вычислительного процесса
на отдельные этапы, возможность выполнения которых исполнителем (компьютером)
не вызывает сомнений.
Алгоритм должен быть
формализован по некоторым правилам посредством конкретных изобразительных
средств. К ним относятся следующие способы записи алгоритмов: словесный,
формульно-словесный, графический, язык операторных схем, алгоритмический
язык.
Наибольшее распространение
благодаря своей наглядности получил графический (блок-схемный) способ
записи алгоритмов.
Блок-схемой
называется графическое изображение логической структуры алгоритма, в котором
каждый этап процесса обработки информации представляется в виде геометрических
символов (блоков), имеющих определенную конфигурацию в зависимости от
характера выполняемых операций. Перечень символов, их наименование, отображаемые
ими функции, форма и размеры определяются ГОСТами.
При всем многообразии
алгоритмов решения задач в них можно выделить три основных вида вычислительных
процессов:
- линейный;
- ветвящийся;
- циклический.
Линейным
называется такой вычислительный процесс, при котором все этапы решения
задачи выполняются в естественном порядке следования записи этих этапов.
Ветвящимся
называется такой вычислительный процесс, в котором выбор направления обработки
информации зависит от исходных или промежуточных данных (от результатов
проверки выполнения какого-либо логического условия).
Циклом называется
многократно повторяемый участок вычислений. Вычислительный процесс, содержащий
один или несколько циклов, называется циклическим.
По количеству выполнения циклы делятся на циклы с определенным (заранее
заданным) числом повторений и циклы с неопределенным числом повторений.
Количество повторений последних зависит от соблюдения некоторого условия,
задающего необходимость выполнения цикла. При этом условие может проверяться
в начале цикла — тогда речь идет о цикле с предусловием, или в конце —
тогда это цикл с постусловием.
Существует множество определений понятия «алгоритм»:
- «процедура, которая принимает любой из возможных входных экземпляров задачи и преобразует его в соответствии с требованиями, указанными в условии задачи» [1];
- «точное предписание, однозначно определяющее вычислительный процесс, ведущий от варьируемых начальных данных к искомому результату» [2];
- «конечный набор правил, однозначно раскрывающих содержание и последовательность выполнения операций для систематического решения определенного класса задач за конечное число шагов» [3];
- «A computable set of steps to achieve a desired result» [4].
Из определений вытекают свойства алгоритма [5]:
- дискретность. В определениях 3 и 4 говорится, что алгоритм состоит из отдельных действий или правил. Алгоритм обладает дискретностью, если его можно разделить на отдельные этапы (части, команды);
- детерминированность (определенность). Алгоритм обладает свойством детерминированности, если для одних и тех же наборов исходных данных он будет выдавать один и тот же результат, т.е. результат однозначно определяется исходными данными (на это свойство указывается в определении 3);
- результативность. Свойство результативности означает, что алгоритм должен выдавать результат за конечное число шагов. О том, что число шагов должно быть конечным говорится в определениях 3 и 4;
- массовость. В определениях 1, 2, 3 говорится о некоторых классах задач (входных экземплярах задачи, варьируемых начальных данных) на которых алгоритм должен работать алгоритм. Это означает, что набор исходных данных, на которых алгоритм должен выдавать верное решение, заранее ограничен;
- правильность. Под правильностью понимается соответствие результатов работы алгоритма условию задачи (определение 1). Казалось бы, очень сомнительное свойство, ведь выше было описано свойство результативности, однако, программа должна не просто выдавать результат, а результат правильный.
Теперь покажем, что конкретный алгоритм обладает этими свойствами. В качестве примера, возьмем алгоритм, изображенный на рис. 1 в виде блок-схемы [6].
 Рис 1 Блок-схема алгоритма проверки правильности расстановки скобок
Рис 1 Блок-схема алгоритма проверки правильности расстановки скобок
Приведенный алгоритм проверяет правильность расстановки скобок, если скобки расставлены правильно – то каждой закрывающей скобке предшествует соответствующая открывающая, а каждой открывающей соответствует закрывающая.
Суть алгоритма заключается в подсчете глубины вложенности скобок друг в друга. Если в какой-то момент глубина получает значение меньше нуля – то скобки расставлены неправильно. Если просмотрены все символы строки, но счетчик не равен нулю – то в строке есть не закрытые скобки (расставлены неправильно). В противном случае скобки расставлены правильно.
Можно сказать, что алгоритм обладает свойством дискретности, так как весь алгоритм разбит на отдельные части (на блок-схеме это хорошо видно).
Доказать детерминированность алгоритма, достаточно сложно, например, когда алгоритм содержит части, которые выполняются параллельно, но не будем сейчас на этом останавливаться. Скажем, что в данном случае программа является детерминированной, т.к. не содержит фрагментов, зависящих от времени выполнения, т.е. сколько бы мы не тестировали алгоритм на одной и той же строке результат не изменится.
Чтобы показать результативность алгоритма, в данном случае достаточно заметить, что любой путь из начальной вершины в конечную содержит блок вывода результата. Перед блоком «конец» алгоритм содержит лишь 2 альтернативные ветви, каждая из которых выводит некоторый результат.
Алгоритм обладает свойством массовости, т.к. исходными данными для него может быть любая конечная последовательность символов. Алгоритм не обладал бы этим свойством, если бы работал лишь ограниченном наборе исходных данных, например на строках «()» и «())», но на остальных наборах не работал или работал не правильно.
Проверить свойство правильности алгоритма достаточно просто, для этого можно взять несколько примеров исходных данных, для которых результат очевиден и протестировать алгоритм на них, но доказать правильность алгоритма достаточно сложно. Доказательство правильности называется верификацией и явно выходит за рамки этой статьи.
В этой статье мы разобрались с тем, что такое алгоритм и какими основными свойствами он должен обладать. К теме алгоритмов я обязательно вернусь в будущих статьях.
Литература:
- Скиена С. Алгоритмы. Руководство по разработке. 2-е изд.: Пер. с англ. — СПб.: БХВ-Петербург. 2011. — 720 с.: ил.
- ГОСТ 19781-74. Единая система программной документации. Термины и определения. Утв. пост. Госкомстата № 2051 от 08.05.08.
- Семененко В. А., Скуратович Э.К. Информатика и вычислительная техника: Учебное пособие. — М.: МГИУ, 2006. — 272 с
- Paul E. B. Dictionary of Algorithms, Data Structures, and Problems. [Электронный ресурс]/ Paul E. B. – режим доступа: https://xlinux.nist.gov/dads/HTML/algorithm.html. Дата обращения: 07.05.2017.
- Елабуга: изд-во ЕГПУ, 2009.- 72 с. 97 . Лизунова Е.М. Теория алгоритмов. Лекции 2007
- ГОСТ 19.701-90. ЕСПД. Схемы алгоритмов, программ, данных систем. Условные обозначения и правила выполнения
- Обзор литературы по алгоритмам
Valera
Высший разум
(218911)
8 лет назад
Свойства алгоритма
Алгоритм обладает следующими свойствами:
1. Дискретность. Это свойство состоит в том, что алгоритм должен представлять процесс решения задачи как последовательное выполнение простых шагов. При этом для выполнения каждого шага алгоритма требуется конечный отрезок времени, т. е. преобразование исходных данных в результат осуществляется во времени дискретно.
2. Определенность. Каждое правило алгоритма должно быть четким, однозначным.
3. Результативность. Алгоритм должен приводить к решению за конечное число шагов.
4. Массовость. Алгоритм решения задачи разрабатывается в общем виде, т. е. он должен быть применим для некоторого класса задач, различающихся лишь исходными данными.
5. Правильность. Алгоритм правильный, если его выполнение дает правильные результаты решения поставленной задачи.
SerGo
Высший разум
(101320)
8 лет назад
• Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
• Понятность алгоритма — алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые входят в его систему команд.
• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.
• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Свойства алгоритма
Евгенний Парфенюк
Ученик
(153)
2 недели назад
Дискретность (прерывность, раздельность) – алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
• Определенность – каждое правило алгоритма должно быть четким, однозначным и не оставлять места для произвола. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
• Понятность алгоритма — алгоритм, составленный для конкретного исполнителя, должен включать только те команды, которые входят в его систему команд.
• Результативность (конечность) – алгоритм должен приводить к решению задачи за конечное число шагов.
• Массовость – алгоритм решения задачи разрабатывается в общем виде, то есть, он должен быть применим для некоторого класса задач, различающихся только исходными данными. При этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Алгоритм. Свойства алгоритмов.
Блок-схемы. Алгоритмические языки
Код ОГЭ: 1.3.1. Алгоритм, свойства алгоритмов, способы записи алгоритмов.
Блок-схемы. Представление о программировании
Понятие алгоритма является одним из основных понятий вычислительной математики и информатики.
■ Алгоритм
— строго определенная последовательность действий для некоторого исполнителя, приводящая к поставленной цели или заданному результату за конечное число шагов.
Любой алгоритм составляется в расчете на конкретного исполнителя с учетом его возможностей. Исполнитель — субъект, способный исполнять некоторый набор команд. Совокупность команд, которые исполнитель может понять и выполнить, называется системой команд исполнителя.
Для выполнения алгоритма исполнителю недостаточно только самого алгоритма. Выполнить алгоритм — значит применить его к решению конкретной задачи, т. е. выполнить запланированные действия по отношению к определенным входным данным. Поэтому исполнителю необходимо иметь исходные (входные) данные — те, что задаются до начала алгоритма.

В результате выполнения алгоритма исполнитель должен получить искомый результат — выходные данные, которые исполнитель выдает как результат выполненной работы. В процессе работы исполнитель может создавать и использовать данные, не являющиеся выходными, — промежуточные данные.
Свойства алгоритмов
Алгоритм должен обладать определенными свойствами. Наиболее важные свойства алгоритмов:
- Дискретность. Процесс решения задачи должен быть разбит на последовательность отдельных шагов — простых действий, которые выполняются одно за другим в определенном порядке. Каждый шаг называется командой (инструкцией). Только после завершения одной команды можно перейти к выполнению следующей.
- Конечность. Исполнение алгоритма должно завершиться за конечное число шагов; при этом должен быть получен результат.
- Понятность. Каждая команда алгоритма должна быть понятна исполнителю. Алгоритм должен содержать только те команды, которые входят в систему команд его исполнителя.
- Определенность (детерминированность). Каждая команда алгоритма должна быть точно и однозначно определена. Также однозначно должно быть определено, какая команда будет выполняться на следующем шаге. Результат выполнения команды не должен зависеть ни от какой дополнительной информации. У исполнителя не должно быть возможности принять самостоятельное решение (т. е. он исполняет алгоритм формально, не вникая в его смысл). Благодаря этому любой исполнитель, имеющий необходимую систему команд, получит один и тот же результат на основании одних и тех же исходных данных, выполняя одну и ту же цепочку команд.
- Массовость. Алгоритм предназначен для решения не одной конкретной задачи, а целого класса задач, который определяется диапазоном возможных входных данных.
Способы представления алгоритмов:
- словесная запись (на естественном языке). Алгоритм записывается в виде последовательности пронумерованных команд, каждая из которых представляет собой произвольное изложение действия;
- блок–схема (графическое изображение). Алгоритм представляется с помощью специальных значков (геометрических фигур) — блоков;
- формальные алгоритмические языки. Для записи алгоритма используется специальная система обозначений (искусственный язык, называемый алгоритмическим);
- псевдокод. Запись алгоритма на основе синтеза алгоритмического и обычного языков. Базовые структуры алгоритма записываются строго с помощью элементов некоторого базового алгоритмического языка.
Словесная запись алгоритма
Произвольное изложение этапов алгоритма на естественном языке имеет свои недостатки. Словесные описания строго не формализуемы, поэтому может быть нарушено свойство определенности алгоритма: исполнитель может неточно понять описание этапа алгоритма. Словесная запись достаточно многословна. Сложные задачи трудно представить в словесной форме.
■ Пример 1. Записать в словесной форме правило деления обыкновенных дробей.
Решение.
Шаг 1. Числитель первой дроби умножить на знаменатель второй дроби.
Шаг 2. Знаменатель первой дроби умножить на числитель второй дроби.
Шаг 3. Записать дробь, числителем которой являет результат выполнения шага 1, знаменателем — результат выполнения шага 2.
Описанный алгоритм применим к любым двум обыкновенным дробям. В результате его выполнения будут получены выходные данные — результат деления двух дробей (исходных данных).
Формальные исполнители алгоритма
Формальный исполнитель — это исполнитель, который выполняет все команды алгоритма строго в предписанной последовательности, не вникая в его смысл, не внося ничего в алгоритм и ничего не отбрасывая. Обычно под формальным исполнителем понимают технические устройства, автоматы, роботов и т. п. Компьютер можно считать формальным исполнителем.
Программы на языке произвольного формального исполнителя могут состоять только из элементарных команд, которые входят в его систему (которые исполнитель «понимает»).
Исполнитель может иметь свою среду (например, систему координат, клеточное поле и др.). Среда исполнителя — это совокупность объектов, над которыми он может выполнять определенные действия (команды), и связей между этими объектами. Алгоритмы в этой среде выполняются исполнителем по шагам.
■ Пример 2. Исполнитель Крот имеет следующую систему команд:
- вперед k — продвижение на указанное число шагов вперед;
- поворот s — поворот на s градусов по часовой стрелке;
- повторить m [команда1 … командаN] — повторить m раз серию указанных команд.
Какой след оставит за собой исполнитель после выполнения следующей последовательности команд?
Повторить 5 [вперед 10 поворот 72]
Решение. Команда вынуждает исполнителя 5 раз повторить набор действий: пройти 10 шагов вперед и повернуть на 72° по часовой стрелке. Так как поворот происходит на один и тот же угол, то за весь путь исполнитель повернет на 5 х 72° = 360°. Поскольку все отрезки пути одинаковой длины и сумма внешних углов любого многоугольника составляет 360°, то в результате будет оставлен след в форме правильного пятиугольника со стороной в 10 шагов исполнителя.
Заметим, что если увеличить количество повторов серии команд, то исполнитель будет повторно передвигаться по тем же отрезкам (произойдет повторное движение по тому же пятиугольнику).
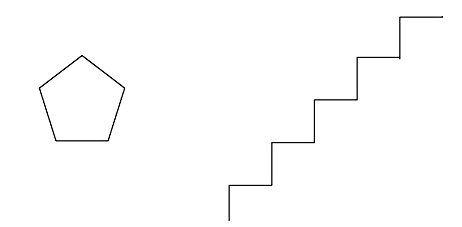
■ Пример 3. В системе команд предыдущего исполнителя Крот сформировать алгоритм вычерчивания пятиступенчатой лестницы (длина ступеньки — 10 шагов исполнителя).
Решение. За каждый шаг цикла должно происходить 4 действия: движение вперед на 10 шагов исполнителя, поворот на 90° по часовой стрелке, еще 10 шагов вперед и поворот на 90° против часовой стрелки (= 270° по часовой). В результате за один шаг цикла формируется ломаная из двух отрезков длиной 10 под прямым углом. За пять таких шагов сформируется 5–ступенчатая лестница (ломаная будет содержать 10 звеньев).
Повторить 5 [вперед 10 поворот 90 вперед 10 поворот 270]
Блок–схема
Блок–схема — наглядный способ представления алгоритма. Блок–схема отображается в виде последовательности связанных между собой функциональных блоков, каждый из которых соответствует выполнению одного или нескольких действий. Определенному типу действия соответствует определенная геометрическая фигура блока. Линии, соединяющие блоки, определяют очередность выполнения действий. По умолчанию блоки соединяются сверху вниз и слева направо. Если последовательность выполнения блоков должна быть иной, используются направленные линии (стрелки).
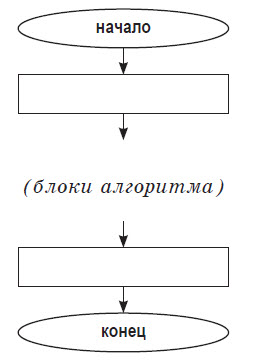
Основные элементы блок–схемы алгоритма:

Общий вид блок–схемы алгоритма:
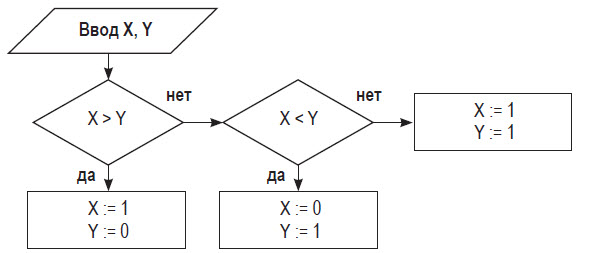
■ Пример 4. Алгоритм целочисленных преобразований представлен в виде фрагмента блок–схемы. Знаком := в нем обозначен оператор присваивания некоторого значения указанной переменной. Запись X := 1 означает, что переменная Х принимает значение 1.
Определить результат работы алгоритма для исходных данных Х = 7, Y = 12.
Решение.
- Блок ввода данных определит исходные значения переменных Х и Y (7 и 12 соответственно).
- В первом условном блоке осуществляется сравнение значений Х и Y. Поскольку условие, записанное в блоке, неверно (7 < 12), происходит переход по линии «нет».
- Во втором условном блоке выполняется второе сравнение, которое для исходных данных оказывается верным. Происходит переход по линии «да».
- Вычисляется результат выполнения алгоритма: X := 0, Y := 1.
Ответ: X := 0, Y := 1.
Алгоритмические языки
Алгоритмический язык — это искусственный язык (система обозначений), предназначенный для записи алгоритмов. Он позволяет представить алгоритм в виде текста, составленного по определенным правилам с использованием специальных служебных слов. Количество таких слов ограничено. Каждое служебное слово имеет точно определенный смысл, назначение и способ применения. При записи алгоритма служебные слова выделяют полужирным шрифтом или подчеркиванием.
В алгоритмическом языке используются формальные конструкции, но нет строгих синтаксических правил для записи команд. Различные алгоритмические языки различаются набором служебных слов и формой записи основных конструкций.
Алгоритмический язык, конструкции которого однозначно преобразуются в команды для компьютера, называется языком программирования. Текст алгоритма, записанный на языке программирования, называется программой.
Псевдокод
Псевдокод занимает промежуточное положение между естественным языком и языками программирования. Пример псевдокода — учебный алгоритмический язык. Алфавит учебного алгоритмического языка является открытым. Существенным достоинством этого языка является то, что его служебные слова, конструкции и правила записи алгоритма весьма схожи с теми, что применяются в распространенных языках программирования. Благодаря этому учебный алгоритмический язык позволяет легче освоить основы программирования.
Служебные слова учебного алгоритмического языка:
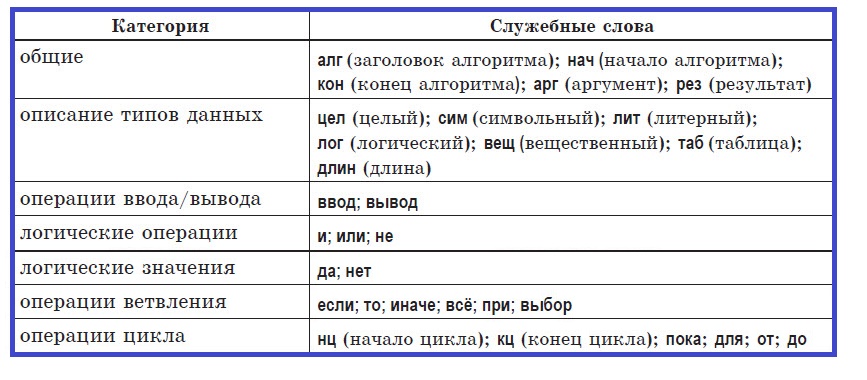
Стандартная структура алгоритма
Представление алгоритма на алгоритмическом языке (в том числе и языке программирования) состоит из двух частей. Первая часть — заголовок — задает название алгоритма и включает описание переменных, которые используются в нем. Вторая часть — тело алгоритма — содержит последовательность команд алгоритма.
Общий вид записи алгоритма на учебном алгоритмическом языке:

В начале заголовка записывается служебное слово алг, после чего указывается имя алгоритма. Описание переменных, являющихся аргументами алгоритма и его результатами, приводится после названия в круглых скобках.
В следующих строках конкретизируют, какие именно переменные являются аргументами алгоритма (входными данными), а какие — его результатами (выходными данными). Для этого после служебного слова арг приводится список имен переменных–аргументов; в следующей строке после служебного слова рез приводится список имен переменных–результатов.
Между служебными словами нач и кон размещается тело алгоритма — конечная последовательность команд, выполнение которых предписывает алгоритм. Команды алгоритма записывают одну за одной в отдельных строках. В случае необходимости можно записать две или более команд в одной строке, тогда соседние команды разделяют точкой с запятой. Если в алгоритме применяются промежуточные переменные, их описание приводят в начальной строке тела алгоритма рядом со словом нач.
Примеры заголовков алгоритмов:

В первом примере алгоритм имеет название Объем_шара, один вещественный аргумент Радиус и один вещественный результат Объем. Во втором примере алгоритм под названием Choice имеет три аргумента — целые M и N и логический b, а также два результата — вещественные Var1 и Var2.
Пример алгоритма вычисления гипотенузы прямоугольного треугольника:

На вход алгоритму даются два вещественных аргумента a и b (величины катетов), результатом является вещественная переменная с (гипотенуза). Для ее расчета используется функция вычисления квадратного корня sqrt.
Описание величин и действия над ними
При описании алгоритма необходимо указать названия (обозначения) всех величин, которые будут в нем найдены или использованы.
При представлении алгоритма решения в виде блок–схемы выбранные обозначения величин приводятся отдельно от блок–схемы (как объяснение к ней). Если алгоритм представлен на языке программирования, то характеристика обрабатываемых величин включается в программу. Учебный алгоритмический язык также предусматривает описание величин, используемых в алгоритме.
Все величины в алгоритме разделяют на постоянные (константы) и переменные. Константа не может изменять свои значения в процессе работы алгоритма. Переменная может приобретать различные значения, которые сохраняются до тех пор, пока она не получит новое значение. Переменным величинам назначают имена. Таким образом, переменная — это именуемая величина, которая в процессе выполнения алгоритма может приобретать и хранить различные значения.
В алгоритмическом языке не существует специальных правил именования переменных. Однако их названия не должны совпадать со служебными словами алгоритмического языка. Во многих языках программирования для имен можно использовать только латинские буквы, цифры, знак подчеркивания. Имена обязательно должны начинаться с буквы, при этом строчные и прописные буквы в именах не различаются. В одном алгоритме не могут существовать разные объекты с одинаковыми именами. Все имена являются уникальными. Имена переменных и констант стараются выбирать так, чтобы они напоминали их смысл. Например, имена переменных и констант: S, p12, result, итог.
При представлении алгоритма на алгоритмическом языке именуются не только величины, но и сам алгоритм, и другие объекты. Имя алгоритма выбирают так же, как и имена переменных.
Величина — переменная, с которой связывается определенное множество значений. Этой величине присваивается имя (в языках программирования его называют идентификатор).
Значение — то, чему равна переменная в конкретный момент. Значение переменной можно задать двумя способами: присваиванием и с помощью процедуры ввода.
Тип переменной определяет диапазон всех значений, которые может принимать данная переменная, и допустимые для нее операции. Существует несколько предопределенных типов переменных. К стандартным типам относятся числовые, литерные и логические типы.
Числовой тип предназначен для обработки числовых данных. Различают целый и вещественный числовые типы. Целый тип в учебном алгоритмическом языке обозначается служебным словом цел, к нему относятся целые числа некоторого определенного диапазона. Они не могут иметь дробной части, даже нулевой. Число 123,0 является не ц?
