Какое сочетательное свойство сложения и умножения
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42
4 · 2 · 3 = 3 · 2 · 4 = 24
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c)
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a — b) = m · a — m · b
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a — b) · m = a · m — b · m
Переход от умножения:
m · (a + b) и m · (a — b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a — m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a — m · b
к умножению:
m · (a + b) и m · (a — b)
называется вынесением общего множителя за скобки.
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.
Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).
Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
abc = cba,
17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).
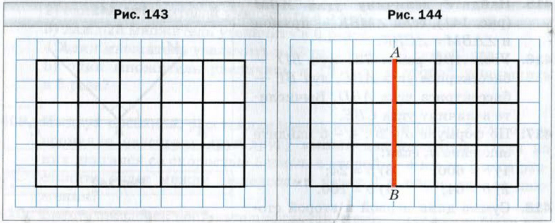
На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).
Равенсто 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
ab + ac = a(b + c).
Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:
P = 2(a + b).
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b − c) = ab − ac
Пример 1. Вычислите удобным способом:
1) 25 * 867 * 4;
2) 329 * 75 + 329 * 246.
Решение.
1) Используем переместительное, а затме сочетательное свойства умножения:
25 * 867 * 4 = 867 * (25 * 4) = 867 * 100 = 86 700.
2) Имеем:
329 * 754 + 329 * 246 = 329 * (754 + 246) = 329 * 1 000 = 329 000.
Пример 2. Упростите выражение:
1) 4a * 3b;
2) 18m − 13m.
Решение.
1) Используя переместительное и сочетательное свойства умножения, получаем:
4a * 3b = (4 * 3) * ab = 12ab.
2) Используя распределительное свойство умножения относительно вычитания, получаем:
18m − 13m = m(18 − 13) = m * 5 = 5m.
Пример 3. Запишите выражение 5(2m + 7) так, чтобы оно не содержало скобок.
Решение.
Согласно распределительному свойству умножения относительно сложения имеем:
5(2m + 7) = 5 * 2m + 5 * 7 = 10m + 35.
Такое преобразование называют раскрытием скобок.
Пример 4. Вычислите удобным способом значение выражения 125 * 24 * 283.
Решение. Имеем:
125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8) * (3 * 283) = 1 000 * 849 = 849 000.
Пример 5. Выполните умножение: 3 сут 18 ч * 6.
Решение. Имеем:
3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.
При решении примера было использовано распределительное свойство умножения относительно сложения:
3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.
Числа, действия с числами
Мы определили сложение, умножение, вычитание и деление целых чисел. Эти действия (операции) обладают рядом характерных результатов, которые называются свойствами. В этой статье мы рассмотрим основные свойства сложения и умножения целых чисел, из которых следуют все остальные свойства этих действий, а также свойства вычитания и деления целых чисел.
Основные свойства сложения целых чисел
Для начала нужно сказать, что все свойства сложения натуральных чисел справедливы для сложения целых чисел. Это обусловлено тем, что натуральные числа являются составной частью целых чисел. Перечислим основные свойства сложения.
Во-первых, сложение целых чисел обладает переместительным свойством. Это свойство заключается в том, что результат сложения двух целых чисел не зависит от порядка следования слагаемых. То есть, для двух целых чисел a и b справедливо равенство a+b=b+a. К примеру, в силу рассмотренного свойства справедливо равенство 3+21=21+3; также справедливо равенство (−564)+45=45+(−564); сумма целых отрицательных чисел −2 и −6 754 равна сумме (−6 754)+(−2).
Во-вторых, сложение целых чисел обладает сочетательным свойством. Сочетательное свойство заключается в том, что результат сложения целого числа с суммой двух целых чисел равен результату сложения суммы двух первых целых чисел с третьим. Это свойство сложения проще усвоить, когда оно записано в буквенном виде: a+(b+c)=(a+b)+c, где a, b, c – произвольные целые числа. Приведем пару примеров. Рассмотренное свойство сложения целых чисел позволяет говорить о справедливости равенства 54+((−17)+(−3 400))=(54+(−17))+(−3 400); аналогично сумма вида 10+((−100)+1 000) равна сумме (10+(−100))+1 000.
Следует заметить, что значение сочетательного свойства сложения целых чисел состоит еще и в том, что оно позволяет однозначно определить сложение трех, четырех и большего количества целых чисел.
Для сложения целых чисел характерны еще несколько очень важных свойств.
Одно из них связано с существованием нуля. Это свойство сложения целых чисел утверждает, что прибавление к любому целому числу нуля не изменяет это число. Запишем данное свойство сложения с помощью букв: a+0=a и 0+a=a (это равенство справедливо в силу переместительного свойства сложения), a – любое целое число. Можно услышать, что целое число нуль называют нейтральным элементом по сложению. Приведем пару примеров. Сумма целого числа −78 и нуля равна −78; если к нулю прибавить целое положительное число 999, то в результате получим число 999.
Сейчас мы дадим формулировку еще одного свойства сложения целых чисел, которое связано с существованием противоположного числа для любого целого числа. Сумма любого целого числа с противоположным ему числом равна нулю. Приведем буквенную форму записи этого свойства: a+(−a)=0, где a и −a – противоположные целые числа. Например, сумма 901+(−901) равна нулю; аналогично сумма противоположных целых чисел −97 и 97 равна нулю.
Основные свойства умножения целых чисел
Умножению целых чисел присущи все свойства умножения натуральных чисел. Перечислим основные из этих свойств.
Умножение целых чисел обладает переместительным свойством. Оно утверждает, что результат умножения двух целых чисел не зависит от порядка следования множителей. То есть, для любых целых чисел a и b справедливо равенство a·b=b·a. Например, произведение целых чисел 56 и −9 равно произведению чисел −9 и 56; также справедливо равенство (−678)·(−92)=(−92)·(−678).
Для умножения целых чисел характерно сочетательное свойство. В буквенном виде оно записывается так: a·(b·c)=(a·b)·c, где a, b, c – произвольные целые числа. Приведем пример. В силу переместительного свойства умножения целых чисел можно говорить о справедливости равенства (−12)·(56·90 003)=((−12)·56)·90 003.
Сочетательное свойство умножения целых чисел позволяет определить умножение трех и большего количества целых чисел.
Также как нуль является нейтральным целым числом относительно сложения, единица является нейтральным целым числом относительно умножения целых чисел. То есть, умножение любого целого числа на единицу не изменяет умножаемое число. Так 1·a=a, где a – любое целое число. Последнее равенство можно переписать в виде a·1=a, это нам позволяет сделать переместительное свойство умножения. Приведем два примера. Произведение целого числа 556 на 1 равно 556; произведение единицы и целого отрицательного числа −78 равно −78.
Следующее свойство умножения целых чисел связано с умножением на нуль. Результат умножения любого целого числа a на нуль равен нулю, то есть, a·0=0. Также справедливо равенство 0·a=0 в силу переместительного свойства умножения целых чисел. В частном случае при a=0 произведение нуля на нуль равно нулю.
Для умножения целых чисел также справедливо свойство, обратное к предыдущему. Оно утверждает, что произведение двух целых чисел равно нулю, если хотя бы один из множителей равен нулю. В буквенном виде это свойство можно записать так: a·b=0, если либо a=0, либо b=0, либо и a и b равны нулю одновременно.
Распределительное свойство умножения целых чисел относительно сложения
Совместно сложение и умножение целых чисел нам позволяет рассматривать распределительное свойство умножения относительно сложения, которое связывает два указанных действия. Использование сложения и умножения совместно открывает дополнительные возможности, которых мы были бы лишены, рассматривая сложение отдельно от умножения.
Итак, распределительное свойство умножения относительно сложения гласит, что произведение целого числа a на сумму двух целых чисел a и b равно сумме произведений a·b и a·c, то есть, a·(b+c)=a·b+a·c. Это же свойство можно записать в другом виде: (a+b)·c=a·c+b·c.
Распределительное свойство умножения целых чисел относительно сложения вместе с сочетательным свойством сложения позволяют определить умножение целого числа на сумму трех и большего количества целых чисел, а далее – и умножение суммы целых чисел на сумму.
Также заметим, что все остальные свойства сложения и умножения целых чисел могут быть получены из указанных нами свойств, то есть, они являются следствиями указанных выше свойств.
Свойства вычитания целых чисел
Мы знаем, что вычитание целых чисел является действием, обратным к сложению целых чисел. Вычитание – это действие, при котором находится неизвестное слагаемое по известной сумме и известному слагаемому (об этом мы говорили в разделе теории смысл вычитания целых чисел). То есть, целое число c является разностью целых чисел a и b, когда сумма b+c равна a.
Такое определение разности, а также свойства сложения целых чисел, позволили нам доказать, что разность целых чисел a и b равна сумме числа a и числа −b, противоположного b. То есть, a−b=a+(−b) (доказательство этого равенства приведено в разделе теории правило вычитания целых чисел).
Из полученного равенства, а также из свойств сложения и умножения целых чисел вытекают следующие свойства вычитания целых чисел (a, b и c – произвольные целые числа):
- Вычитание целых чисел в общем случае НЕ обладает переместительным свойством: a−b≠b−a.
- Разность равных целых чисел равна нулю: a−a=0.
- Свойство вычитания суммы двух целых чисел из данного целого числа: a−(b+c)=(a−b)−c.
- Свойство вычитания целого числа из суммы двух целых чисел: (a+b)−c=(a−c)+b=a+(b−c).
- Распределительное свойство умножения относительно вычитания: a·(b−c)=a·b−a·c и (a−b)·c=a·c−b·c.
- И все другие свойства вычитания целых чисел.
Свойства деления целых чисел
Рассуждая о смысле деления целых чисел, мы выяснили, что деление целых чисел – это действие, обратное умножению. Мы дали такое определение: деление целых чисел – это нахождение неизвестного множителя по известному произведению и известному множителю. То есть, целое число c мы называем частным от деления целого числа a на целое число b, когда произведение c·b равно a.
Данное определение, а также все рассмотренные выше свойства операций над целыми числами позволяют установить справедливость следующих свойств деления целых чисел:
- Никакое целое число нельзя делить на нуль.
- Свойство деления нуля на произвольное целое число a, отличное от нуля: 0:a=0.
- Свойство деления равных целых чисел: a:a=1, где a – любое целое число, отличное от нуля.
- Свойство деления произвольного целого числа a на единицу: a:1=a.
- В общем случае деление целых чисел НЕ обладает переместительным свойством: a:b≠b:a.
- Свойства деления суммы и разности двух целых чисел на целое число: (a+b):c=a:c+b:c и (a−b):c=a:c−b:c, где a, b, и c такие целые числа, что и a и b делится на c, и c отлично от нуля.
- Свойство деления произведения двух целых чисел a и b на целое число c, отличное от нуля: (a·b):c=(a:c)·b, если a делится на c; (a·b):c=a·(b:c), если b делится на c; (a·b):c=(a:c)·b=a·(b:c), если и a и b делятся на c.
- Свойство деления целого числа a на произведение двух целых чисел b и c (числа a, b и c такие, что деление a на b·c возможно): a:(b·c)=(a:b)·c=(a:c)·b.
- Любые другие свойства деления целых чисел.
Список литературы.
- Виленкин Н.Я. и др. Математика. 6 класс: учебник для общеобразовательных учреждений.
- Курош А.Г. Курс высшей алгебры.
Некогда разбираться?
Закажите решение
Умножение, сложение, вычитание и деление — основные операции с целыми числами. Результаты этих операций с любыми целыми числами обладают рядом характеристик. Иначе говоря, операции умножения, сложения, вычитания и деления целых чисел обладают свойствами. Данная статья посвящена рассмотрению основных свойств умножения, сложения, вычитания и деления целых чисел.
Сложение целых чисел. Основные свойства
Все свойства сложения натуральных чисел оказываются справедливы и для целых чисел. Ведь множество целых чисел ℤ включает в себя множество натуральных чисел ℕ. Приведем ниже основные свойства сложения.
Коммутативное свойство сложения
Переместительное (коммутативное свойство) или переместительный закон.
От перемены мест слагаемых сумма не меняется.
a+b=b+a
Согласно этому свойству, справедливо равенство:
35+251=251+35
Свойство коммутативности работает вне зависимости от знака.
-528+3700=3700+-528
Ассоциативное свойство сложения
Сочетательное (ассоциативное свойство) или сочетательный закон.
Сложение целого числа с суммой двух целых чисел эквивалентно сложению суммы двух первых чисел с третьим.
a+b+c=a+b+c
Примечание: данное свойство применимо и для большего количества слагаемых.
Вот несколько примеров. Согласно свойству ассоциативности справедливы равенства:
64+81+(-49)=64+81+(-49)=64+81+(-49);
(128+(-75))+96=128+((-75)+96).
Свойства сложения, связанные с числом 0
1. Число нуль — нейтральный по сложению элемент.
Прибавление нуля к любому целому числу не меняет этого числа.
a+0=a
2. Сумма любого целого числа и противоположного ему числа равна нулю.
a+(-a)=0
Умножение целых чисел. Основные свойства
Как и в случае со сложением, все свойства умножения натуральных чисел переносятся на целые числа.
Для умножения также действуют переместительный и сочетательный (коммутативный и ассоциативный) законы.
Переместительное свойство умножения
От перемены мест множителей произведение не меняется.
a·b=b·a
Приведем пример. Очевидно, что произведение целых чисел 2·3 эквивалентно произведению 3·2.
Сочетательное свойство умножения
Сочетательное свойство для умножения эквивалентно сочетательному свойству сложения. В буквенном виже оно записывается следующим образом:
a·(b·c)=(a·b)·c
a, b, c — произвольные целые числа.
Примечание: данное свойство применимо и для большего количества множителей.
В соответствии с этим свойством можно говорить о справедливости следующих равенств:
-12·3·8=-12·3·8;
119·((-251)·36)=(119·(-251))·36.
Умножение числа на нуль
Результатом умножения любого целого числа на нуль является число нуль.
a·0=0
Справедливо и обратное: произведение двух целых чисел a и b равно нулю, если хотя бы один из множителей равен нулю.
a·b=0 если a=0 или b=0.
Умножение числа на единицу
Умножение любого целого числа на единицу дает в результате это число. Иными словами, умножение на единицу не изменяет умножаемое число.
a·1=a
Распределительное свойство умножения относительно суммы.
Произведение целого числа a на сумму двух чисел b и c равно сумме произведений a·b и a·c.
a·(b+c)=a·b+a·c
Данное свойство часто используется при упрощении выражений, одновременно содержащих как операции сложения, так и умножения.
В совокупности с ассоциативным свойством и распределительным законом можно легко расписать произведение целого числа на сумму из более чем трех слагаемых, а также произведение сумм.
Вычитание целых чисел. Основные свойства
Вычитание — действие, обратное сложению. Число c является разностью двух чисел a и b тогда, когда сумма b+c равна a. Можно сказать, что разность чисел a и b — это сумма чисел a и -b. Свойства вычитания являются следствием свойств сложения и умножения.
Основные свойства вычитания
- Вычитание чисел не обладает переместительным свойством за исключением случая, когда a=b. a-b≠b-a.
- Разность целых чисел, равных друг другу: a-a=0.
- Вычитание суммы двух чисел из другого числа: a-(b+c)=a-b-c.
- Вычитание целого числа из суммы: a+b-c=a-c+b=a+(b-c).
- Распределительное свойство умножения относительно вычитания: a·(b-c)=a·b-a·c.
Деление целых чисел. Основные свойства
Деление — операция, обратная умножению. Число c называется частным от деления чисел a и b, когда произведение b·c равно a. Запишем основные свойства деления целых чисел.
Основные свойства деления
- Деление на нуль невозможно.
- Деление нуля на число: 0a=0.
- Деление равных чисел: aa=1.
- Деление на единицу: a1=a.
- Для деления переместительное свойства не выполняется: ab≠ba.
- Деление суммы и разности на число: a±bc=ac±bc.
- Деление произведения на число: a·bc=ac·b, если a делится на c; a·bc=a·bс, если b делится на c; a·bc=a·bс=ac·b, если a и b делятся на c.
- Деление числа на произведение: ab·c=ab·1c=ac·1b.
