Какое основное свойство пропорции
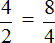
Вступление. Тема урока
Слово «пропорция» происходит от латинского корня и означает «соразмерность». Люди часто используют его в повседневной жизни. Говорят, например, о пропорциях человеческого тела или о пропорциях в кулинарии. Сегодня мы узнаем, что вкладывают в это слово математики.
Пропорция. Иллюстрирующий пример и определение
Рассмотрим два отношения. Мы помним, что отношение – это частное двух чисел.
Заметим, что и в первом и во втором случае значение частного равно трем. Перед нами два равных отношения. Запишем равенство.
Пятнадцать так относится к пяти, как двадцать четыре к восьми. Такое равенство и называют пропорцией. Иногда это равенство записывают в виде равенства обыкновенных дробей.
Сформулируем определение: равенство двух отношений называют пропорцией.
Как записывают и читают пропорции. Что называют средними и крайними членами пропорции
С помощью букв пропорцию можно записать:
Отношение a к b равно отношению c к d. Иногда пропорцию читают по-другому: «a так относится к b, как c относитсяк d». Участвующие в пропорции числа называют членами пропорции. Считают, что все члены отличны от нуля.
Числа a и d называют крайним членами пропорции, а числа b и c– средними членами. Действительно, в первом варианте записи числа b и c находятся посередине, а числа a и d с краю.
Основное свойство пропорции. Иллюстрирующий пример и формулировка
В рассмотренной ранее пропорции найдем произведение ее средних и крайних членов.
Заметим, что два полученных произведения равны.
Сформулируем основное свойство пропорции в общем виде.
В верной пропорции произведение крайних членов равно произведению средних.
Верно и обратное утверждение.
Если произведение крайних членов равно произведению средних членов пропорции, то пропорцияверна.
Упражнение. Найти неизвестный член пропорции
Найдем неизвестный член пропорции, то есть решим пропорцию.
Числа 0,5 и 13 – это крайние члены; числа aи 2 – это средние члены. Воспользуемся основным свойством пропорции.
Упражнение. Решить пропорцию
Решим пропорцию.
Используя основное свойство пропорции, получим:
Чтобы избавиться от десятичной дроби в знаменателе, умножим и числитель, и знаменатель дроби на 10. Сократим полученную дробь на 4, а затем еще раз на 4.
Х = 60.
Упражнение. Узнать является ли данная пропорция верной
Проверить являются ли данные пропорции верными:
В этом задании нужно проверить, действительно ли выполняется равенство между отношениями.
Решение
Найдем произведение средних и произведение крайних членов для каждой пропорции. Если полученные произведения равны, то пропорция верна. В противном же случае, пропорция является неверной.
верная пропорция, т. к.
неверная пропорция, т. к.
Как сконструировать новые верные пропорции из данной
Если в верной пропорции поменять местами средние или крайние члены, то получившееся новые пропорции тоже верны.
Это так потому, что при такой перестановке произведение крайних и средних членов не изменяется.
Разберем пример. Из данной пропорции получить две новые, переставив крайние и средние члены. Сначала переставим средние члены (рис. 1).
Рис. 1. Перестановка средних членов
Действительно, произведение средних и крайних не изменилось, значит, полученная пропорция верна. Переставим крайние члены (рис. 2).
Рис. 2. Перестановка крайних членов
И в этом случае произведение средних и крайних не изменилось. Мы получили верную пропорцию.
Список литературы
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012.
- Мерзляк А.Г., Полонский В.В., Якир М.С. Математика 6 класс. – Гимназия. 2006.
- Депман И.Я., Виленкин Н.Я. За страницами учебника математики. – М.: Просвещение, 1989.
- Рурукин А.Н., Чайковский И.В. Задания по курсу математика 5–6 класс. – М.: ЗШ МИФИ, 2011.
- Рурукин А.Н., Сочилов С.В., Чайковский К.Г. Математика 5–6. Пособие для учащихся 6-х классов заочной школы МИФИ. – М.: ЗШ МИФИ, 2011.
- Шеврин Л.Н., Гейн А.Г., Коряков И.О., Волков М.В. Математика: Учебник-собеседник для 5–6 классов средней школы. – М.: Просвещение, Библиотека учителя математики, 1989.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Математика (Источник).
- Интернет-портал Math-portal.ru (Источник).
Домашнее задание
- Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. Математика 6. – М.: Мнемозина, 2012: № 762 (а, г, д), № 765, № 777.
- Другие задания: № 767, № 775.
Продолжаем изучать соотношения. В данном уроке мы познакомимся с пропорцией.
Что такое пропорция?
Пропорцией называют равенство двух отношений. Например, отношение ![]() равно отношению
равно отношению ![]()
![]()
Данная пропорция читается следующим образом:
Десять так относится к пяти, как два относится к одному
Предположим, что в классе 10 девочек и 5 мальчиков

Запишем отношение десяти девочек к пяти мальчикам:
10 : 5
Преобразуем данное отношение в дробь
![]()
Выполнив деление в этой дроби, мы получим 2. То есть десять девочек так будут относиться к пяти мальчикам, что на одного мальчика будет приходиться две девочки

Теперь рассмотрим другой класс в котором две девочки и один мальчик

Запишем отношение двух девочек к одному мальчику:
2 : 1
Преобразуем данное отношение в дробь:
![]()
Выполнив деление в этой дроби, мы снова получим 2. То есть две девочки так будут относиться к одному мальчику, что на этого одного мальчика будут приходиться две девочки:

Можно сделать вывод, что отношение ![]() пропорционально отношению
пропорционально отношению ![]() . Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
. Поэтому оно и читалось как «десять так относится к пяти, как два относится к одному».
В нашем примере десять девочек так относятся к пяти мальчикам, как и две девочки относятся к одному мальчику.
Пример 2. Рассмотрим отношение 12 девочек к 3 мальчикам

а также отношение 12 девочек к 2 мальчикам

Данные отношения не являются пропорциональными. Другими словами, мы не можем записать, что ![]() , поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
, поскольку первое отношение, как видно на рисунке показывает, что на одного мальчика приходятся четыре девочки, а второе отношение показывает, что на одного мальчика приходятся шесть девочек.
Поэтому отношение ![]() не пропорционально отношению
не пропорционально отношению ![]() .
.
![]()
Из рассмотренных примеров видно, что пропорция составляется из дробей. Первая рассмотренная нами пропорция ![]() состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
состоит из двух дробей. Если выполнить деление в этих дробях, то получим, что 2=2. Понятно, что 2 равно 2.
Вторая рассмотренная нами пропорция была ![]() . Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями
. Мы пришли к выводу, что она составлена неправильно, поэтому поставили между дробями ![]() и
и ![]() знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
знак не равно (≠). Если выполнить деление в этих дробях, получим числа 4 и 6. Понятно, что 4 не равно 6.
Рассмотрим пропорцию . Данная пропорция составлена правильно, поскольку отношения и равны между собой:
Можно проверить это, выполнив деление в этих дробях, то есть разделить 4 на 2, а 8 на 4. В результате с двух сторон получатся двойки. А 2 равно 2
![]()
2 = 2
Все числа, находящиеся в пропорции (числители и знаменатели обеих дробей) называются членами пропорции. Эти члены подразделяются на два вида: крайние члены и средние члены.
В нашей пропорции ![]() крайние члены это 4 и 4, а средние члены это 2 и 8
крайние члены это 4 и 4, а средние члены это 2 и 8
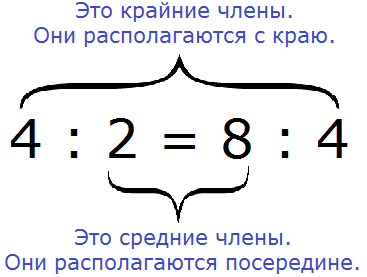
Почему крайние члены называют крайними, а средние средними? Если записать пропорцию не в дробном, а в обычном виде, то сразу станет всё понятно:
4 : 2 = 8 : 4
Числа 4 и 4 располагаются с краю, поэтому их назвали крайними, а числа 2 и 8 располагаются посередине, поэтому их назвали средними:
С помощью переменных пропорцию можно записать так:
![]()
Данное выражение можно прочесть следующим образом:
a так относится к b, как c относится к d
Смысл данного предложения уже понятен. Речь идет о членах, участвующих в соотношении. a и d — это крайние члены пропорции, b и c — средние члены пропорции.
Основное свойство пропорции
Основное свойство пропорции выглядит следующим образом:
Произведение крайних членов пропорции равно произведению её средних членов.
Мы знаем, что произведение это ни что иное, как обычное умножение. Чтобы проверить правильно ли составлена пропорция, нужно перемножить её крайние и средние члены. Если произведение крайних членов будет равно произведению средних членов, то такая пропорция составлена правильно.
Например, проверим правильно ли составлена пропорция ![]() . Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
. Для этого перемножим её крайние и средние члены. Легко заметить, что крайние и средние члены пропорции располагаются «крест-накрест», поэтому в умножении нет ничего сложного. Перемножаем члены пропорции «крест-накрест»:
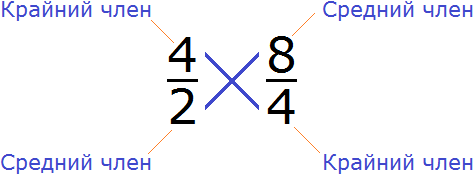
4 × 4 = 16 — произведение крайних членов пропорции равно 16.
2 × 8 = 16 — произведение средних членов пропорции так же равно 16.
4 × 4 = 2 × 8
16 = 16
4 × 4 = 2 × 8 — произведение крайних членов равно произведению средних членов. Значит пропорция ![]() составлена правильно.
составлена правильно.
Пример 2. Проверить правильно ли составлена пропорция ![]()
Проверим равно ли произведение крайних членов пропорции произведению её средних членов. Перемножим члены пропорции крест-накрест:
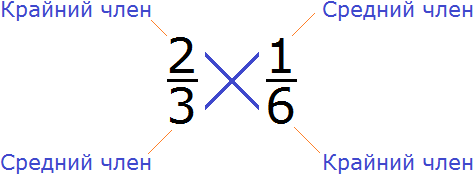
2 × 6 = 12 — произведение крайних членов пропорции равно 12
3 × 1 = 3 — произведение средних членов пропорции равно 3
2 × 6 ≠ 3 × 1
12 ≠ 3
2 × 6 ≠ 3 × 1 — произведение крайних членов пропорции НЕ равно произведению её средних членов. Значит пропорция ![]() составлена неправильно.
составлена неправильно.
Поэтому в пропорции ![]() разумнее заменить знак равенства (=) на знак не равно (≠)
разумнее заменить знак равенства (=) на знак не равно (≠)
![]()
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Навигация по записям
| 1. | Запись пропорции по словесному описанию Сложность: | 1 |
| 2. | Выбор отношений, равных данному отношению Сложность: | 2 |
| 3. | Верные пропорции (целые числа) Сложность: | 2 |
| 4. | Истинность пропорции Сложность: | 1 |
| 5. | Крайние или средние члены пропорции Сложность: | 1 |
| 6. | Вычисление неизвестного члена пропорции 1 Сложность: | 2 |
| 7. | Вычисление неизвестного члена пропорции 2 Сложность: | 2 |
| 8. | Истинность пропорции Сложность: | 2 |
| 9. | Выбор отношений для составления пропорции Сложность: | 2 |
| 10. | Основное свойство пропорции (десятичные дроби) Сложность: | 2 |
| 11. | Уравнение (десятичные дроби) Сложность: | 2 |
| 12. | Уравнение (десятичные дроби и смешанное число) Сложность: | 2 |
| 13. | Составление пропорции Сложность: | 2 |
| 14. | Уравнение (обыкновенные дроби) Сложность: | 3 |
| 15. | Неизвестное число (смешанные числа и обыкновенная дробь) Сложность: | 5 |
| 16. | Составление пропорций (буквы) Сложность: | 3 |
| 17. | Неизвестное четвёртое число Сложность: | 6 |
Методические материалы
| Номер | Название | Описание |
|---|---|---|
| 1. | Технологическая карта |
Теория
Задания
| Номер | Название | Вид | Сложность | Баллы | Описание |
|---|---|---|---|---|---|
| 1. | Запись пропорции по словесному описанию | 1 вид — рецептивный | лёгкое | 1 Б. | Запись пропорции по словесному описанию, отношения в виде дроби. |
| 2. | Выбор отношений, равных данному отношению | 2 вид — интерпретация | лёгкое | 2 Б. | Выбор отношений, равных данному отношению. |
| 3. | Верные пропорции (целые числа) | 2 вид — интерпретация | лёгкое | 2 Б. | Выбор верных равенств. |
| 4. | Истинность пропорции | 1 вид — рецептивный | лёгкое | 1 Б. | Следует определить, является ли равенство верным. |
| 5. | Крайние или средние члены пропорции | 1 вид — рецептивный | лёгкое | 1 Б. | Крайние или средние члены пропорции. |
| 6. | Вычисление неизвестного члена пропорции 1 | 2 вид — интерпретация | среднее | 2 Б. | Целые числа, x находится в знаменателе. |
| 7. | Вычисление неизвестного члена пропорции 2 | 2 вид — интерпретация | среднее | 2 Б. | Целые числа, x находится в числителе. |
| 8. | Истинность пропорции | 1 вид — рецептивный | среднее | 2 Б. | Пропорция записана с помощью знаков деления. |
| 9. | Выбор отношений для составления пропорции | 2 вид — интерпретация | среднее | 2 Б. | Выбор отношений для составления пропорции. |
| 10. | Основное свойство пропорции (десятичные дроби) | 2 вид — интерпретация | среднее | 2 Б. | Следует проверить истинность равенства, используя основное свойство пропорции. Выбор правильного ответа. |
| 11. | Уравнение (десятичные дроби) | 2 вид — интерпретация | среднее | 2 Б. | Вычисление крайнего члена пропорции. |
| 12. | Уравнение (десятичные дроби и смешанное число) | 2 вид — интерпретация | среднее | 2 Б. | Вычисление среднего члена пропорции. |
| 13. | Составление пропорции | 2 вид — интерпретация | среднее | 2 Б. | Составление пропорции, использование основного свойства пропорции, отношения в виде дроби. |
| 14. | Уравнение (обыкновенные дроби) | 2 вид — интерпретация | среднее | 3 Б. | Вычисление крайнего члена пропорции. |
| 15. | Неизвестное число (смешанные числа и обыкновенная дробь) | 2 вид — интерпретация | сложное | 5 Б. | Вычисление среднего члена пропорции. |
| 16. | Составление пропорций (буквы) | 2 вид — интерпретация | сложное | 3 Б. | Составление пропорций. |
| 17. | Неизвестное четвёртое число | 2 вид — интерпретация | сложное | 6 Б. | По данным трём числам найти четвёртое такое, чтобы из чисел можно было составить пропорцию. |
Тесты
Проверочные тесты (скрыты от учеников)
| Номер | Название | Рекомендованное время: | Сложность | Баллы | Описание |
|---|---|---|---|---|---|
| 1. | Домашняя работа по теме Пропорция. Основное свойство пропорции | 00:20:00 | среднее | 7 Б. | Запись пропорции по словесному описанию, отношения в виде дроби. Выбор отношений для составления пропорции (целые числа). Вычисление неизвестного члена пропорции (целые числа). Уравнение (десятичные дроби). |
| 2. | Проверочная работа по теме Пропорция. Основное свойство пропорции | 00:25:00 | среднее | 12 Б. | Запись пропорции по словесному описанию с использованием знака деления. Выбор отношений, равных данному отношению. Следует проверить истинность равенства, используя основное свойство пропорции. Выбор правильного ответа. Уравнение (десятичные дроби). Вычисление среднего члена пропорции. Неизвестное число (целое число и смешанные числа). Вычисление крайнего члена пропорции. |
