Какое бинарное отношение обладает свойством симметричности
У этого термина существуют и другие значения, см. Отношение.
Бина́рное (двухместное) отноше́ние (соответствие[1][2]) — отношение между двумя множествами и , то есть всякое подмножество декартова произведения этих множеств: [3]. Бинарное отношение на множестве — любое подмножество , такие бинарные отношения наиболее часто используются в математике, в частности, таковы равенство, неравенство, эквивалентность, отношение порядка.
Связанные определения[править | править код]
Свойства отношений[править | править код]
Бинарное отношение на некотором множестве может обладать различными свойствами, например:
- рефлексивность: ,
- антирефлексивность (иррефлексивность): ,
- корефлексивность: ,
- симметричность: ,
- антисимметричность: ,
- асимметричность: ,
- транзитивность: ,
- евклидовость: ,
- полнота (или связность[4]): ,
- связность (или слабая связность[4]): ,
- трихотомия: верно ровно одно из трех утверждений: , или .
Виды отношений[править | править код]
Виды бинарных отношений[править | править код]
- Обратное отношение[уточнить] (отношение, обратное к ) — это двухместное отношение, состоящее из пар элементов , полученных перестановкой пар элементов данного отношения . Обозначается: . Для данного отношения и обратного ему верно равенство: .
- Взаимо-обратные отношения (взаимообратные отношения) — отношения, являющиеся обратными друг по отношению к другу. Область значений одного из них служит областью определения другого, а область определения первого — областью значений другого.
- Рефлексивное отношение — двухместное отношение , определённое на некотором множестве и отличающееся тем, что для любого этого множества элемент находится в отношении к самому себе, то есть для любого элемента этого множества имеет место . Примеры рефлексивных отношений: равенство, одновременность, сходство.
- Антирефлексивное отношение (иррефлексивное отношение; так же, как антисимметричность не совпадает с несимметричностью, иррефлексивность не совпадает с нерефлексивностью) — бинарное отношение , определённое на некотором множестве и отличающееся тем, что для любого элемента этого множества неверно, что оно находится в отношении к самому себе (неверно, что ).
- Транзитивное отношение — двухместное отношение , определённое на некотором множестве и отличающееся тем, что для любых из и следует (). Примеры транзитивных отношений: «больше», «меньше», «равно», «подобно», «выше», «севернее».
- Нетранзитивное отношение[уточнить] — двухместное отношение , определённое на некотором множестве и отличающееся тем, что для любых этого множества из и не следует (). Пример нетранзитивного отношения: «x отец y»
- Симметричное отношение — бинарное отношение , определённое на некотором множестве и отличающееся тем, что для любых элементов и этого множества из того, что находится к в отношении , следует, что и находится в том же отношении к — . Примером симметричных отношений могут быть равенство, отношение эквивалентности, подобие, одновременность.
- Антисимметричное отношение — бинарное отношение , определённое на некотором множестве и отличающееся тем, что для любых и из и следует (то есть и выполняются одновременно лишь для равных между собой членов).
- Асимметричное отношение — бинарное отношение , определённое на некотором множестве и отличающееся тем, что для любых и из следует . Пример: отношения «больше» (>) и «меньше» (<).
- Отношение эквивалентности — бинарное отношение между объектами и , являющееся одновременно рефлексивным, симметричным и транзитивным. Примеры: равенство, равномощность двух множеств, подобие, одновременность.
- Отношение порядка — отношение, обладающие только некоторыми из трёх свойств отношения эквивалентности: отношение рефлексивное и транзитивное, но несимметричное (например, «не больше») образует нестрогий порядок, а отношение транзитивное, но нерефлексивное и несимметричное (например, «меньше») — строгий порядок.
- Функция одного переменного — бинарное отношение , определённое на некотором множестве, отличающееся тем, что каждому значению отношения соответствует лишь единственное значение . Свойство функциональности отношения записывается в виде аксиомы: .
- Биекция (взаимно-однозначное отношение) — бинарное отношение , определённое на некотором множестве, отличающееся тем, что в нём каждому значению соответствует единственное значение , и каждому значению соответствует единственное значение .
Операции над отношениями[править | править код]
Так как отношения, заданные на фиксированной паре множеств и суть подмножества множества , то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных , :
,
,
.
Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.
Например, , , то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрогого порядка, а их пересечение пусто.
Кроме перечисленных важное значение имеют ещё операции обращения и умножения отношений, определяемые следующим образом. Если , то обратным отношением называется отношение , определённое на паре , и состоящее из тех пар , для которых . Например, .
Пусть , . Композицией (или произведением) отношений и называется отношение такое, что:
.
Например, для отношения строгого порядка на множестве натуральных числе его умножение на себя определено следующим образом: .
Бинарные отношения и называются перестановочными, если . Для любого бинарного отношения , определённого на , имеет место , где символом обозначено равенство, определённое на . Однако равенство не всегда справедливо.
Имеют место следующие тождества:
Аналоги последних двух тождеств для пересечения отношений не имеют места.
Примечания[править | править код]
- ↑ Цаленко М. Ш. Соответствие // Математическая энциклопедия. — 1985. — Т. 5 (Слу-Я). — С. 77.
- ↑ Соответствие. Большая российская энциклопедия.
- ↑ Кострикин А. И. Введение в алгебру. Основы алгебры.. — М.: Физматлит, 1994. — С. 47-48. — 320 с. — ISBN 5-02-014644-7.
- ↑ 1 2 Дубов Ю. А., Травкин СИ., Якимец В. Н. Многокритериальные модели формирования и выбора вариантов систем. — М.: Наука, 1986. (с. 48)
Литература[править | править код]
- Мальцев, А. И. Алгебраические системы. — М.: Наука, 1970. — 392 с. — 17 500 экз.
- Алескеров Ф.Т., Хабина Э.Л., Шварц Д.А. Бинарные отношения, графы и коллективные решения. — М.: Учебники Высшей школы экономики, 2006. — 300 с.
- Пухначев Ю. В., Попов Ю. П. Кн. 1: Множества, отображения, отношения, последовательности, ряды, функции, свойства функций, дифференциальное и интегральное исчисление, функции многих переменных // Математика без формул. — Изд. 6-е, испр. — М.: URSS, 2017. — 231 с. — ISBN 978-5-9710-3871-9.
Бинарные отношения в общем случае обладают свойствами рефлексивности, антирефлексивности, симметричности, антисимметричности, транзитивности, связности.
1. Рефлексивное отношение – отношение , в котором для любого выполняется
.
Другая запись такого отношения .
Главная диагональ матрицы такого отношения содержит только единицы.
Примером рефлексивного отношения является отношение «подобие треугольников, заданное на множестве всех треугольников евклидовой плоскости»: каждый треугольник подобен себе самому;
— отношения « » и «иметь общий делитель».
2. Антирефлексивное отношение – отношение , в котором ни для какого не выполняется
или .
Главная диагональ матрицы такого отношения содержит только нули.
Примером антирефлексивного отношения является отношение «перпендикулярность прямых, заданных на множестве всех прямых евклидовой плоскости»:
— никакая прямая не перпендикулярна себе самой;
— отношения «<» и «быть сыном».
Отношение «быть симметричным относительно оси » не является ни рефлексивным, ни антирефлексивным: точка плоскости симметрична сама себе, если она лежит на оси и несимметрична сама себе в противном случае.
3. Симметричное отношение – отношение , в котором для пары
из следует или .
Иначе говоря, для любой пары отношение симметричности выполняется либо в обе стороны, либо не выполняется вообще. Матрица симметричного отношения симметрична относительно главной диагонали: для любых и . Для симметричного отношения .
Примером симметричного отношения является отношение «быть симметричным относительно оси », которое является симметричным: если первая точка симметрична второй, то и вторая симметрична первой;
отношение «проживать в одном доме», заданное на множестве всех жителей некоторого города: если живет в одном доме с , то живет в одном доме с .
4. Антисимметричное отношение – отношение ,в котором для
пары из и следует, что или
.
Примером антисимметричного отношения является отношение « », заданное на множестве действительных чисел: действительно, если , и , то .
5. Транзитивное отношение – отношение ,в котором для любых
из и следует или
.
Примером транзитивного отношения являются отношения «равенство», « », «жить в одном городе»: действительно если ; если ; если и живут в городе и и живут в городе , то и также живут в городе .
Отношение «быть сыном» нетранзитивно: если является сыном и является сыном то это не значит, что является сыном . Отношение «пересекаться», то есть «иметь непустое пересечение», заданное на системе множеств, также нетранзитивно. Например, пересекается с , пересекается с , однако и не пересекаются.
Транзитивное замыкание отношения. Транзитивное замыкание отношения – это отношение , которое определяется следующим образом: , если в существует цепочка из элементов , в которой между соседними элементами выполнено отношение : .
Если транзитивно, то . Действительно, если , то(цепочка состоит из двух элементов и ), поэтому . Если же , тосуществует цепочка . Но так как транзитивно, то , поэтому . Из включения в обе стороны следует .
Транзитивным замыканием отношения «быть сыном» является отношение «быть прямым потомком», являющееся объединением отношений «быть сыном», «быть внуком», «быть правнуком» и т.д. Транзитивным замыканием отношения «иметь общую стену» для жильцов дома является отношение «жить на одном этаже».
6. Связное (полное) отношение – отношение , в котором для пары
из следует или ,
или .
Примером связного (полного) отношения является отношение «быть старше», заданное на множестве родных братьев и сестер некоторой семьи: если , то либо старше , либо старше .
Рассмотренные свойства можно определить с помощью выражений:
1. , 2. , 3. , 4. ,
5. (где – композиция отношений), 6. .
Если даны два отношения и , то операции над этими отношениями сводятся к операциям над ними, аналогичные операциям над множествами:
объединению ; пересечению ; разности ; симметрической разности . Дополнение отношения ( ) будет равно .
На основании приведенных выше свойств отношений можно дать им ряд определений.
Отношение частичного порядка – отношение, которое рефлексивно, антисимметрично и транзитивно.
Отношение линейного порядка – отношение частичного порядка, которое связно.
Отношение строгого порядка – отношение, которое антирефлексивно, антисимметрично и транзитивно.
Отношение строгого линейного порядка – связное отношение строгого порядка.
В теории множеств важную роль играют два вида специальных бинарных отношений: эквивалентности и порядка, прообразами которых являются понятия равенства, предшествования и предпочтения.
Пусть
задано на множестве
,
.
1.
Рефлексивность:
.
Отношение на
множествеXназываетсярефлексивным, если для любого
имеет место
,
то есть каждый элемент находится в
отношениик
самому себе.
Матрица рефлексивного отношения имеет
единичную главную диагональ, а граф
рефлексивного отношения – имеет петлю
возле каждого своего элемента.
Например:
,
,
,
.
На множестве людей: “быть родственником”,
”обучаться в одной студенческой группе
”.
На множестве множеств: AB, A=B.
2. Антирефлексивность: .
Отношение на
множествеXназываетсяантирефлексивным, если не
существует
такого, чтоимеет место
,
то есть ни один элемент не находится
в отношениик самому себе.
Матрица антирефлексивного отношения
имеет нулевую главную диагональ, а граф
– не имеет ни одной петли.
Например:
,
,
.
На множестве людей: “быть родителем”,
”быть ребенком”.
На множестве множеств: AB, AB.
3. Нерефлексивность:
.
4. Симметричность: .
Отношение на
множествеXназываетсясимметричным, если для всех
и
из Х, из принадлежности(x,y)
отношениюследует, чтои
принадлежит отношению.
Матрица симметричного отношения
симметрична относительно главной
диагонали, а граф – для
каждой дуги (x,y)
существует обратная дуга(y,x).
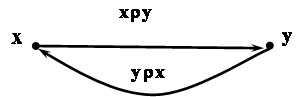
Например:
,
,
.
На множестве людей: “быть родственником”,
”обучаться в одной студенческой группе
”. Отношение
«
брат
»
является симметричным
на множестве
мужчин и не является
симметричным на
множествевсех людей.
На множестве множеств:
,
.
5. Антисимметричность: .
Отношение на
множествеXназываетсяантисимметричным, если для всех
и
из Х, из принадлежности(x,y)
и(y,x)
отношениюследует, что
.
Матрица антисимметричного отношения
не имеет ни одной симметричной единицы
относительно главной диагонали, а граф
– длякаждой
дуги (x,y)
не существует
обратная дуга(y,x)
и наоборот.
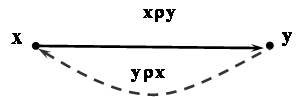
Свойства симметричности и антисимметричности
не являются взаимоисключающими, примером
может служить отношения равенства на
множестве натуральных чисел.
Например:
,
,
,
,
.
На множестве людей: “быть выше”, ”быть
равным”.
На множестве множеств:
,
,
.
6. Транзитивность: .
Отношение
на множестве
называетсятранзитивным, если для
всех
измножества
,из принадлежности
и
отношениюследует, что
также принадлежит.
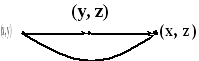
Например:
,
,
,
,
,
.
На множестве людей: “быть выше”,
”обучаться в одной студенческой группе”.
На множестве множеств:
,
,
.
Отношение rна множестве Xнеявляется
транзитивным,если
существует, хотя бы один пример того,что для некоторых х,y,zмножества Х
из принадлежности (x,y)
и(y,z)
отношениюrне
следует,что (x,z)такжепринадлежитr.
Например.
1)
.
Отношение 
неявляется
транзитивным,потому что
из принадлежности этому отношению пар
и
,
неследует,что
и пара
принадлежит
отношению 
.
2) Пусть задано двухэлементное
множество 
определим
все бинарные отношения на этом множестве:
.
Для всех отношений, заданных на множестве
,
определить наличие или отсутствие
основных свойств.
Введем следующие обозначения:
а) рефлексивность– Р;
б) антирефлексивность– АР;
в) симметричность– С;
г) антисимметричность– АС;
д) транзитивность– Т.
№ |
| Р | АР | С | АС | Т |
1 |
| — | + | + | + | + |
2 |
| — | — | + | + | + |
3 |
| — | + | — | + | + |
4 |
| — | + | — | + | + |
5 |
| — | — | + | + | + |
6 |
| — | — | — | + | + |
7 |
| — | — | — | + | + |
8 |
| + | — | + | + | + |
9 |
| — | + | + | — | — |
10 |
| — | — | — | + | + |
11 |
| — | — | — | + | + |
12 |
| — | — | + | — | — |
13 |
| + | — | — | + | + |
14 |
| + | — | — | + | + |
15 |
| — | — | + | — | — |
16 |
| + | — | + | — | + |
Отношение порядка– антисимметрично,
транзитивно.
Отношение нестрого порядка(
)
– рефлексивно,
антисимметрично,
транзитивно.
Например:
,
.
На множестве множеств:
,
.
Отношение строгого порядка(
)
– антирефлексивно,
антисимметрично,
транзитивно.
Например:
,
.
На множестве множеств: “
”.
— “xпредшествуетyв смысле
отношения строгого порядка”,
— “xпредшествуетyв смысле
отношения нестрогого
порядка”.
Два элемента
и
некоторого упорядоченного множества
(множества, на котором существует
отношение порядка) сравнимы
между собой, если
предшествует
,
и/или 
предшествует
в смыслеотношения
порядка.
Если в упорядоченном множестве
существует пара элементов xиy,
для которойни
непредшествует
,
ни 
не предшествует
,
тогда говорят, что эти два элементанесравнимы
между собой в смысле этого.
В отношениях полногопорядка все
элементы сравнимы между собой, а в
отношенияхчастичногопорядка не
все элементы сравнимы между собой.
Например:
Отношения полного порядка:
,
.
Отношения частичного порядка:
,
,
на множестве множеств:
,
,
.
Отношение эквивалентности(
) – рефлексивно,
симметрично,
транзитивно.
Класс эквивалентностидля элемента
:
.
Например:
,
.
На множестве людей: “иметь
одно имя”, ”обучаться в
одной студенческой группе”.
На множестве множеств:
.
Отношение эквивалентности
разбивает
–множество,
на котором задано отношение нанепересекающиеся, которые
называют классами эквивалентности.
Элементы, принадлежащие
одному классу, находятсямежду собой в отношении
эквивалентности, элементы из разных
классов в отношении эквивалентности
между собой не находятся.
Например:
Отношение
задано на множестве
списком пар
.
Область определения:
.
Область значений:
.
Отношение
– рефлексивно, симметрично, транзитивно,
следовательно, это отношение
эквивалентности.
Классы эквивалентности:
.
Например:
Отношение 
.
Это отношение называют отношением
сравнения по модулю
на множестве натуральных чисел.
означает, что
и
имеют одинаковый остаток при делении
на
.
Отрезок натурального ряда
.
Отношение сравнения по модулю 3 на
:
.
Область определения и область значений:
.
Отношение
– рефлексивно, симметрично, транзитивно.
Отношение
– отношение эквивалентности.
Классы эквивалентности:
.
Пусть
–некоторое
бинарное отношение.
Обратным отношением 
называется отношение, которое
определяется следующим образом:
Обратное отношение получается путём
перестановки значений в парах исходного
отношения.
Пусть
и
– произвольные бинарные
отношения такие, что
где
– некоторые множества.
Композиция отношений
и
– это таке
бинарное отношение 
которое состоит из
упорядоченных пар 
для которых существует
такой элемент, что выполняются
условия: 
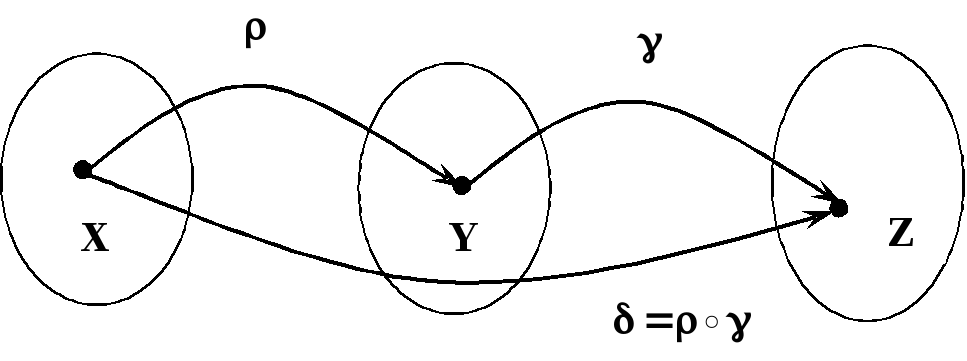
Например.
.
.
.
.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Свойства отношений:
1) рефлексивность;
2)симметричность;
3)транзитивность.
4)связанность.
Отношение R на множестве Х называется рефлексивным, если о каждом элементе множества Х можно сказать, что он находится в отношении R с самим собой: хRх. Если отношение рефлексивно, то в каждой вершине графа имеется петля. И обратно, граф, каждая вершина которого содержит петлю, представляет собой граф рефлексивного отношения.
Примерами рефлексивных отношений являются и отношение «кратно» на множестве натуральных чисел (каждое число кратно самому себе), и отношение подобия треугольников (каждый треугольник подобен самому себе), и отношение «равенства» (каждое число равно самому себе) и др.
Существуют отношения, не обладающие свойством рефлексивности, например, отношение перпендикулярности отрезков: ab, ba (нет ни одного отрезка, о котором можно сказать, что он перпендикулярен самому себе). Поэтому на графе данного отношения нет ни одной петли.
Не обладает свойством рефлексивности и отношение «длиннее» для отрезков, «больше на 2» для натуральных чисел и др.
Отношение R на множестве Х называется антирефлексивным, если для любого элемента из множества Х всегда ложно хRх: .
Существуют отношения, не являющиеся ни рефлексивными, ни антирефлексивными. Примером такого отношения может служить отношение «точка х симметрична точке у относительно прямой l», заданное на множестве точек плоскости. Действительно, все точки прямой l симметричны сами себе, а точки, не лежащие на прямой l, себе не симметричны.
Отношение R на множестве Х называется симметричным, если выполняется условие: из того, что элемент х находится в отношении с элементом y, следует, что и элемент y находится в отношении R с элементом х: xRyyRx .
Граф симметричного отношения обладает следующей особенностью: вместе с каждой стрелкой, идущей от х к y, граф содержит стрелку, идущую от y к х (рис. 35).
Примерами симметричных отношений могут быть следующие: отношение «параллельности» отрезков, отношение «перпендикулярности» отрезков, отношение «равенства» отрезков, отношение подобия треугольников, отношение «равенства» дробей и др.
Существуют отношения, которые не обладают свойством симметричности.
Действительно, если отрезок х длиннее отрезка у, то отрезок у не может быть длиннее отрезка х. Граф этого отношения обладает особенностью: стрелка, соединяющая вершины, направлена только в одну сторону.
Отношение R называют антисимметричным, если для любых элементов х и y из истинности xRy следует ложностьyRx: : xRyyRx.
Кроме отношения «длиннее» на множестве отрезков существуют и другие антисимметричные отношения. Например, отношение «больше» для чисел (если х больше у, то у не может быть больше х), отношение «больше на» и др.
Существуют отношения, которые не обладают ни свойством симметричности, ни свойством антисимметричности.
Отношение R на множестве Х называют транзитивным, если из того, что элемент х находится в отношении R с элементом y, а элемент y находится в отношении R с элементом z, следует, что элемент х находится в отношении R с элементом z: xRy и yRzxRz.
Граф транзитивного отношения с каждой парой стрелок, идущих от х к y и от y к z, содержит стрелку, идущую от х к z.
Свойством транзитивности обладает