Какими свойствами обладают углы четырехугольника вписанные в окружность
Вписанные четырёхугольники и их свойства
Определение 1. Окружностью, описанной около четырёхугольника, называют окружность, проходящую через все вершины четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, вписанным в окружность, или вписанным четырёхугольником.
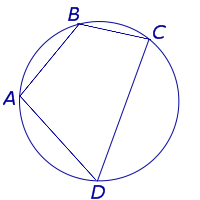
Рис.1
Теорема 1. Если четырёхугольник вписан в окружность, то суммы величин его противоположных углов равны 180°.
Доказательство. Угол ABC является вписанным углом, опирающимся на дугу ADC (рис.1). Поэтому величина угла ABC равна половине угловой величины дуги ADC. Угол ADC является вписанным углом, опирающимся на дугу ABC. Поэтому величина угла ADC равна половине угловой величины дуги ABC. Отсюда вытекает, что сумма величин углов ABC и ADC равна половине угловой величины дуги, совпадающей со всей окружностью, т.е. равна 180°.
Если рассмотреть углы BCD и BAD, то рассуждение будет аналогичным.
Теорема 1 доказана.
Теорема 2 (Обратная к теореме 1). Если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого четырёхугольника можно описать окружность.
Доказательство. Докажем теорему 2 методом «от противного». С этой целью рассмотрим окружность, проходящую через вершины A, B и С четырёхугольника, и предположим, что эта окружность не проходит через вершину D. Приведём это предположение к противоречию. Рассмотрим сначала случай, когда точка D лежит внутри круга (рис.2).
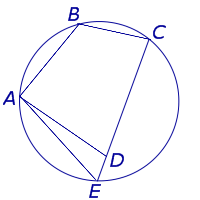
Рис.2
Продолжим отрезок CD за точку D до пересечения с окружностью в точке E, и соединим отрезком точку E с точкой A (рис.2). Поскольку четырёхугольник ABCE вписан в окружность, то в силу теоремы 1 сумма величин углов ABC и AEC равна 180°. При этом сумма величин углов ABC и ADC так же равна 180° по условию теоремы 2. Отсюда вытекает, что угол ADC равен углу AEC. Возникает противоречие, поскольку угол ADC является внешним углом треугольника ADE и, конечно же, его величина больше, чем величина угла AEC, не смежного с ним.
Случай, когда точка D оказывается лежащей вне круга, рассматривается аналогично.
Теорема 2 доказана.
Перечисленные в следующей таблице свойства вписанных четырёхугольников непосредственно вытекают из теорем 1 и 2.
| Фигура | Рисунок | Свойство |
| Окружность, описанная около параллелограмма |  | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |  | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции | 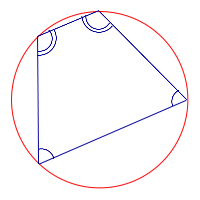 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |  | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник | 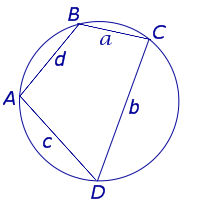 | Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, |
| Окружность, описанная около параллелограмма | |
 | Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба | |
 | Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции | |
 | Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида | |
 | Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник | |
 | Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, |
| Окружность, описанная около параллелограмма |
 Окружность можно описать около параллелограмма тогда и только тогда, когда параллелограмм является прямоугольником. |
| Окружность, описанная около ромба |
 Окружность можно описать около ромба тогда и только тогда, когда ромб является квадратом. |
| Окружность, описанная около трапеции |
 Окружность можно описать около трапеции тогда и только тогда, когда трапеция является равнобедренной трапецией. |
| Окружность, описанная около дельтоида |
 Окружность можно описать около дельтоида тогда и только тогда, когда дельтоид состоит из двух одинаковых прямоугольных треугольников. |
| Произвольный вписанный четырёхугольник |
 Площадь произвольного вписанного четырёхугольника можно найти по формуле Брахмагупты: где a, b, c, d – длины сторон четырёхугольника, |
Теорема Птолемея
Теорема Птолемея. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
Доказательство. Рассмотрим произвольный четырёхугольник ABCD, вписанный в окружность (рис.3).
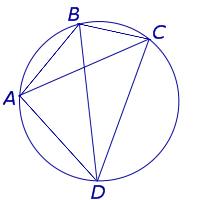
Рис.3
Докажем, что справедливо равенство:
Для этого выберем на диагонали AC точку E так, чтобы угол ABD был равен углу CBE (рис. 4).
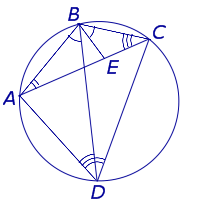
Рис.4
Заметим, что треугольник ABD подобен треугольнику BCE. Действительно, у этих треугольников по два равных угла: угол ABD равен углу CBE (по построению точки E), угол ADB равен углу ACB (эти углы являются вписанными углами, опирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (1) |
Заметим, что треугольник ABE подобен треугольнику BCD. Действительно, у этих треугольников по два равных угла: угол ABE равен углу DBC (углы ABD и EBC равны по построению, угол DBE – общий), угол BAC равен углу BDC (эти углы являются вписанными углами, пирающимися на одну и ту же дугу). Следовательно, справедлива пропорция:
откуда вытекает равенство:
| (2) |
Складывая равенства (1) и (2), получаем:
Теорема Птолемея доказана.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
«Описанная окружность» мы видели, что вокруг всякого треугольника можно описать окружность. То есть, для всякого треугольника найдётся такая окружность, что все три вершины треугольника «сидят» на ней. Вот так:

Вопрос: а можно ли то же самое сказать о четырехугольнике? Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника?
Вот оказывается, что это НЕПРАВДА! НЕ ВСЕГДА четырехугольник можно вписать в окружность. Есть очень важное условие:
 | Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна . |
На нашем рисунке:
Посмотри, углы и лежат друг напротив друга, значит, они противоположные. А что же тогда с углами и ? Они вроде бы тоже противоположные? Можно ли вместо углов и взять углы и ?
Конечно, можно! Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет . Оставшиеся два угла тогда сами собой тоже дадут в сумме . Не веришь? Давай убедимся. Смотри:

Пусть . Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, . То есть — всегда! . Но , → .
Волшебство прямо!
Так что запомни крепко-накрепко:
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна
и наоборот:
Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.
Доказывать всё это мы здесь не будем (если интересно, заглядывай в следующие уровни теории). Но давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна .
Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма? Попробуем сперва «методом тыка».

Вот как-то не получается.
Теперь применим знание:

предположим, что нам как-то удалось посадить на параллелограмм окружность. Тогда непременно должно быть: , то есть .
А теперь вспомним о свойствах параллелограмма:
у всякого параллелограмма противоположные углы равны.
То есть .
У нас получилось, что
→
А что же углы и ? Ну, то же самое конечно.
– вписанный → →
— параллелограмм→ →
Потрясающе, правда?
Получилось, что если параллелограмм вписан в окружность, то все его углы равны , то есть это прямоугольник!

И ещё при этом – центр окружности совпадает с точкой пересечения диагоналей этого прямоугольника. Это, так сказать, в качестве бонуса прилагается.
Ну, вот значит, выяснили, что параллелограмм, вписанный в окружность – прямоугольник.
А теперь поговорим о трапеции. Что будет, если трапецию вписать в окружность? А оказывается, будет равнобедренная трапеция. Почему?

Вот пусть трапеция вписана в окружность. Тогда опять , но из-за параллельности прямых и .
Значит, имеем: → → трапеция равнобокая.
Даже проще чем с прямоугольником, правда? Но запомнить нужно твёрдо – пригодиться: Трапеция, вписанная в окружность – равнобедренная.

Давай ещё раз перечислим самые главные утверждения, касающиеся четырехугольника, вписанного в окружность:
- Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна
- Параллелограмм, вписанный в окружность – непременно прямоугольник и центр окружности совпадает с точкой пересечения диагоналей
- Трапеция, вписанная в окружность – равнобокая.
Вписанный четырехугольник. Средний уровень
Известно, что для всякого треугольника существует описанная окружность (это мы доказывали в теме «Описанная окружность»). Что же можно сказать о четырёхугольнике? Вот, оказывается, что НЕ ВСЯКИЙ четырехугольник можно вписать в окружность, а есть такая теорема:
Четырёхугольник вписан в окружность тогда и только тогда, когда сумма его противоположных углов равна .

На нашем рисунке –
Давай попробуем понять, почему так? Другими словами, мы сейчас докажем эту теорему. Но прежде чем доказывать, нужно понять, как устроено само утверждение. Ты заметил в утверждении слова «тогда и только тогда»? Такие слова означают, что вредные математики впихнули два утверждения в одно.
Расшифровываем:
- «Тогда» означает: Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна .
- «Только тогда» означает: Если у четырёхугольника найдутся два противоположных угла, сумма которых равна , то такой четырехугольник можно вписать в окружность.
Прямо как у Алисы: «думаю, что говорю» и «говорю, что думаю».
А теперь разбираемся, отчего же верно и 1, и 2?
Сначала 1.
Пусть четырехугольник вписан в окружность. Отметим её центр и проведём радиусы и . Что же получится? Помнишь ли ты, что вписанный угол вдвое меньше соответствующего центрального? Если помнишь – сейчас применим, а если не очень – загляни в тему «Окружность. Вписанный угол».

Итак,
— вписанный
— вписанный
Но посмотри: .
Значит,
.
Получаем, что если – вписанный, то
.
Ну, и ясно, что и тоже в сумме составляет . (нужно так же рассмотреть и ).
Теперь и «наоборот», то есть 2.
Пусть оказалось так, что у четырехугольника сумма каких – то двух противоположных углов равна . Скажем, пусть
.

Мы пока не знаем, можем ли описать вокруг него окружность. Но мы точно знаем, что вокруг треугольника мы гарантированно окружность описать можем. Так и сделаем это.
Если точка не «села» на окружность, то она неминуемо оказалась или снаружи или внутри.
Рассмотрим оба случая.
Пусть сначала точка – снаружи. Тогда отрезок пересекает окружность в какой-то точке . Соединим и . Получился вписанный (!) четырехугольник .

Про него уже знаем, что сумма его противоположных углов равна , то есть , а по условию у нас .
Получается, что должно бы быть так, что .
Но это никак не может быть поскольку – внешний угол для и значит, .
А внутри? Проделаем похожие действия. Пусть точка внутри.

Тогда продолжение отрезка пересекает окружность в точке . Снова – вписанный четырехугольник , а по условию должно выполняться , но — внешний угол для и значит, , то есть опять никак не может быть так, что .
То есть точка не может оказаться ни снаружи, ни внутри окружности – значит, она на окружности!
Доказали всю-всю теорему!
Теперь посмотрим, какие же хорошие следствия даёт эта теорема.
Следствие 1
Параллелограмм, вписанный в окружность, может быть только прямоугольником.

Давай-ка поймём, почему так. Пусть параллелограмм вписан в окружность. Тогда должно выполняться .
Но из свойств параллелограмма мы знаем, что .
То есть
И то же самое, естественно, касательно углов и .
Вот и получился прямоугольник – все углы по .

Но, кроме того, есть ещё дополнительный приятный факт: центр окружности, описанной около прямоугольника, совпадает с точкой пересечения диагоналей.
Давай поймём почему. Надеюсь, ты отлично помнишь, что угол, опирающийся на диаметр – прямой.
Ну вот,
— диаметр,
— диаметр
а значит, – центр. Вот и всё.
Следствие 2
Трапеция, вписанная в окружность – равнобедренная.
Докажем?

Пусть трапеция вписана в окружность. Тогда .
Но
То есть
. И так же .

Всё ли мы обсудили? Не совсем. На самом деле есть ещё один, «секретный» способ, как узнавать вписанный четырехугольник. Мы этот способ сформулируем не очень строго (но понятно), а докажем только в последнем уровне теории.
Итак:
Если в четырёхугольнике можно наблюдать такую картинку, как здесь на рисунке (тут углы, «смотрящие» на сторону из точек и , равны), то такой четырехугольник – вписанный.

Это очень важный рисунок – в задачах часто бывает легче найти равные углы, чем сумму углов и .
Несмотря на совершенное отсутствие строгости в нашей формулировке, она верна, и более того, всегда принимается проверяющими ЕГЭ. Ты должен писать примерно так:
« — вписанный» — и всё будет отлично!
Не забывай этот важный признак – запомни картинку, и, возможно, она тебе вовремя бросится в глаза при решении задачки.
Вписанный четырехугольник. Краткое описание и основные формулы
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна
и наоборот:
Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.
Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна .
.
Параллелограмм, вписанный в окружность – непременно прямоугольник, и центр окружности совпадает с точкой пересечения диагоналей.

Трапеция, вписанная в окружность – равнобокая.

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Примеры вписанных четырёхугольников.
Вписанный четырёхугольник — это четырёхугольник, вершины которого лежат на одной окружности. Эта окружность называется описанной. Обычно предполагается, что четырёхугольник выпуклый, но бывают и самопересекающиеся вписанные четырёхугольники. Формулы и свойства, данные ниже, верны только для выпуклых четырёхугольников.
Все треугольники имеют описанные окружности, но не все четырёхугольники.
Примером четырёхугольника, который нельзя вписать в окружность, может служить ромб (если только он не является квадратом). Секция «Свойства» ниже даёт необходимые и достаточные условия, чтобы вокруг четырёхугольника можно было описать окружность.
Специальные случаи[править | править код]
Любые квадраты, прямоугольники, равнобедренные трапеции или антипараллелограммы можно вписать в окружность. Дельтоид можно вписать в том и только в том случае, когда у него два угла прямые. Бицентричный четырёхугольник[en] — это вписанный четырёхугольник, который также является и описанным, а внешне бицентричный четырёхугольник — это вписанный четырёхугольник, который является также
внешне описанным[en].
Свойства[править | править код]
Выпуклый невырожденный четырёхугольник является вписанным тогда и только тогда, когда четыре серединных перпендикуляра, проведённых к каждой из сторон, пересекаются в одной точке[1].
Выпуклый четырёхугольник является вписанным тогда и только тогда, когда противоположные углы в сумме дают 180°, то есть[2].
Теорема была Предложением 22 в книге 3 Евклида Начала[3]. Эквивалентно, выпуклый четырёхугольник является вписанным тогда и только тогда, когда смежный угол равен противоположному внутреннему углу.
Другой критерий для того, чтобы выпуклый четырёхугольник был вписанным, требует, чтобы угол между стороной и диагональю был равен углу между противоположной стороной и другой диагональю[4]. Например,
В выпуклом четырехугольнике пусть — точка пересечения диагоналей, — точка пересечения продолжений сторон и , и пусть — окружность, диаметр которой является отрезком , формирующая точки Паскаля и на сторонах и .
(1) является циклическим четырехугольником тогда и только тогда, когда точки и коллинеарные с центром окружности .[5][6]
(2) является циклическим четырехугольником тогда и только тогда, когда точки и являются серединами сторон и .[5][6]
ABCD является циклическим четырехугольником. E — точка пересечения диагоналей, F — точка пересечения продолжений сторон BC и AD. — окружность, диаметр которой является отрезком EF. P и Q — точки Паскаля, сформированные с помощью окружности .
Неравенство Птолемея утверждает, что произведение длин двух диагоналей p и q четырёхугольника равно сумме произведений противоположных сторон, только если четырёхугольник вписан: [7]
Если две прямые, из которых одна содержит отрезок AC, а другая — отрезок BD, пересекаются в точке E, то четыре точки A, B, C, D лежат на окружности тогда и только тогда, когда[8]
Точка пересечения E может лежать как внутри, так и вне окружности. В первом случае это будет вписанный четырёхугольник ABCD, а во втором — вписанный четырёхугольник ABDC. Если пересечение лежит внутри, равенство означает, что произведение отрезков, на которые точка E делит одну диагональ, равно произведению отрезков другой диагонали. Это утверждение известно как теорема о пересекающихся хордах, поскольку диагонали вписанного четырёхугольника являются хордами описанной окружности.
Выпуклый четырёхугольник ABCD является вписанным тогда и только тогда, когда [9]
Пусть выпуклый четырехугольник, в котором — точка пересечения диагоналей, — точка пересечения продолжений сторон и , — точка пересечения продолжений сторон и . И пусть — окружность девяти точек треугольника . является циклическим четырехугольником тогда и только тогда, когда точка пересечения его средних линий лежит на окружности .[10][11][5]
ABCD — циклический четырехугольник, в котором E — точка пересечения диагоналей, F — точка пересечения продолжений сторон AD и BC, G — точка пересечения продолжений сторон AB и CD. — окружность девяти точек треугольника EFG. Точка T пересечения средних линий ABCD принадлежит окружности .
Площадь[править | править код]
Площадь S вписанного четырёхугольника со сторонами a, b, c, d задаётся формулой Брахмагупты[12]
где p, полупериметр, равен . Утверждение является следствием соотношения Бретшнайдера, поскольку противоположные углы в сумме дают 180°. Если же d= 0, вписанный четырёхугольник становится треугольником, и равенство превращается в формулу Герона.
Вписанный четырёхугольник имеет максимальную площадь среди всех четырёхугольников, имеющих ту же последовательность длин сторон. Это другое следствие соотношения Бретшнайдера. Утверждение можно доказать с помощью математического анализа[13].
Четыре неравные длины, каждая из которых меньше суммы остальных трёх, являются сторонами трёх неконгруэнтных вписанных четырёхугольников[14], и по формуле Брахмагупты все эти треугольники имеют одинаковую площадь. В частности, для сторон a, b, c и d сторона a может быть противоположной любой из сторон b, c или d. Любые два из этих трёх вписанных четырёхугольников имеют диагональ одинаковой длины[15].
Площадь вписанного четырёхугольника с последовательными сторонами a, b, c, d и углом B между сторонами a и b можно выразить формулой[7]
или[16]
где θ — любой угол между диагоналями. Если угол A не является прямым, площадь можно выразить формулой [16]
Ещё одна формула площади [17]
где R — радиус описанной окружности. Прямым следствием будет [18]
,
и неравенство превращается в равенство в том и только в том случае, когда четырёхугольник является квадратом.
Диагонали[править | править код]
Во вписанном четырёхугольнике с вершинами A, B, C, D (в указанной последовательности) и сторонами a = AB, b = BC, c = CD и d = DA длины диагоналей p = AC и q = BD можно выразить через стороны [19][20][15]
и
что даёт равенство Птолемея
Согласно второй теореме Птолемея[19][20],
при тех же обозначениях, что и прежде.
Для суммы диагоналей имеем неравенство [21]
Неравенство становится равенством в том и только в том случае, когда диагонали имеют одинаковую длину, что можно показать, используя неравенство между средним арифметическим и средним геометрическим.
Более того[22],
В любом выпуклом четырёхугольнике две диагонали делят четырёхугольник на четыре треугольника. Во вписанном четырёхугольнике противоположные пары этих четырёх треугольников подобны.
Если M и N являются средними точками диагоналей AC и BD, то[23]
где E и F — точки пересечения противоположных сторон.
Если ABCD — вписанный четырёхугольник и AC пересекает BD в точке P, то [24]
Формулы углов[править | править код]
Для вписанного четырёхугольника со сторонами a, b, c, d, полупериметром p и углом A между сторонами a и d тригонометрические функции угла A равны[25]
Для угла θ между диагоналями выполняется[16]
Если продолжения противоположных сторон a и c пересекаются под углом , то
где p — полупериметр[26]
Формула Парамешвара[править | править код]
Для вписанного четырёхугольника со сторонами a, b, c, d (в указанной последовательности) и полупериметром p радиус описанной окружности задаётся формулой[20][27]
Формула была выведена индийским математиком Ватассери Парамешвара[en] в 15 веке.
Используя формулу Брахмагупты, формулу Парамешвара можно преобразовать в
,
где S — площадь вписанного четырёхугольника.
Антицентр и коллинеарность[править | править код]
Четыре отрезка прямых, перпендикулярных одной стороне вписанного четырёхугольника и проходящих через середину противоположной стороны, пересекаются в одной точке[28][29]. Эта точка пересечения называется антицентром. Антицентр симметричен центру описанной окружности относительно «вершинного центроида». Таким образом, во вписанном четырёхугольнике центр описанной окружности, «вершинный центроид» и антицентр лежат на одной прямой[29].
Если диагонали вписанного четырёхугольника пересекаются в точке P, а середины диагоналей — V и W, то антицентр четырёхугольника является ортоцентром треугольника VWP, а вершинный центроид находится в середине отрезка, соединяющего середины диагоналей [29].
Во вписанном четырёхугольнике «центроид площади» Ga, «центроид вершин» Gv и пересечение P диагоналей лежат на одной прямой. Для расстояний между этими точками выполняется равенство[30]
Другие свойства[править | править код]
- Во вписанном четырёхугольнике ABCD центры вписанных окружностей треугольников ABC, BCD, CDA и DAB являются вершинами прямоугольника. Это одна из теорем, известных как японская теорема. Ортоцентры тех же четырёх треугольников являются вершинами четырёхугольника, равного ABCD. Центроиды этих четырёх треугольников являются вершинами другого вписанного четырёхугольника[4].
- Во вписанном четырёхугольнике ABCD с центром описанной окружности O пусть P — точка пересечения диагоналей AC и BD. Тогда угол APB является средним арифметическим углов AOB и COD. Это является прямым следствием теоремы о вписанном угле и теоремы о внешнем угле треугольника[en].
- Не существует вписанных четырёхугольников с рациональной площадью и неравными рациональными сторонами, образующими арифметическую, либо геометрическую прогрессию[31].
- Если вписанный четырёхугольник имеет длины сторон, образующие арифметическую прогрессию, то четырёхугольник является также внешне описанным[en].
- Если противоположные стороны вписанного четырёхугольника продолжить до пересечения в точках E и F, то внутренние биссектрисы углов в E и F перпендикулярны[14].
Четырёхугольники Брахмагупты[править | править код]
Четырёхугольник Брахмагупты[33] — это вписанный четырёхугольник с целочисленными длинами сторон, целочисленными длинами диагоналей и целочисленной площадью.
Все четырёхугольники Брахмагупты со сторонами a, b, c, d, диагоналями e, f, площадью S, и радиусом описанной окружности R можно получить путём избавления от знаменателя в следующих выражениях (при рациональных параметрах t, u и v):
Свойства ортодиагональных вписанных четырёхугольников[править | править код]
Площадь и радиус описанной окружности[править | править код]
Пусть для вписанного четырёхугольника, являющегося также ортодиагональным (т.е. имеющим перпендикулярные диагонали), пересечение диагоналей делит одну диагональ на отрезки длиной p1 и p2, а другую делит на отрезки длиной q1 и q2. Тогда[34] (первое равенство является Предложением 11 в книге Архимеда «Леммы»)
,
где D — диаметр описанной окружности. Равенство выполняется ввиду того, что диагонали являются перпендикулярными хордами окружности. Отсюда следует, что радиус описанной окружности R удовлетворяет равенству
или, через стороны четырёхугольника
Отсюда также следует, что
Таким образом, согласно формуле Эйлера, радиус можно выразить через диагонали p и q и расстояние x между серединами диагоналей
Формула для площади K вписанного ортодиагонального четырёхугольника можно получить непосредственно через стороны, если скомбинировать теорему Птолемея (см. выше) и формулу площади ортодиагонального четырёхугольника. В результате получим
Другие свойства[править | править код]
- Во вписанном ортодиагональном четырёхугольнике антицентр совпадает с точкой пересечения диагоналей[35].
- Теорема Брахмагупты утверждает, что во вписанном четырёхугольнике, являющемся также ортодиагональным, перпендикуляр от любой стороны через точку пересечения диагоналей делит противоположную сторону пополам[35].
- Если вписанный четырёхугольник является также ортодиагональным, расстояние от центра описанной окружности до любой стороны равно половине длины противоположной стороны [35].
- Во вписанном ортодиагональном четырёхугольнике расстояние между серединами диагоналей равно расстоянию между центром описанной окружности и точкой пересечения диагоналей [35].
См. также[править | править код]
- Теорема о бабочке
- Описанная окружность
- Степень точки относительно окружности
- Таблица хорд Птолемея[en]
- Пятиугольник Роббинса
- Внеописанный четырёхугольник
- Четырёхугольник
Примечания[править | править код]
- ↑ Usiskin, 2008, с. 63–65, Глава 10. Cyclic quadrilaterals.
- ↑ Usiskin, 2008, с. 63–65.
- ↑ Joyce, 1997, с. Book 3, Proposition 22.
- ↑ 1 2 Andreescu, Enescu, 2004, с. 2.3 Cyclic quads.
- ↑ 1 2 3 Fraivert, David; Sigler, Avi & Stupel, Moshe (2019), Necessary and sufficient properties for a cyclic quadrilateral, International Journal of Mathematical Education in Science and Technology, <https://doi.org/10.1080/0020739X.2019.1683772>
- ↑ 1 2 Фрейверт, Д. М. (2019), Новая тема в евклидовой геометрии на плоскости: теория «точек Паскаля», формируемых с помощью окружности на сторонах четырехугольника, Математическое образование: современное состояние и перспективы : материалы Международной научной конференции, <https://libr.msu.by/handle/123456789/9675>
- ↑ 1 2 Durell, Robson, 2003, с. 25.
- ↑ Bradley, 2007, с. 179.
- ↑ Hajja, 2008, с. 103–6.
- ↑ Fraivert, David. New points that belong to the nine-point circle (англ.) // The Mathematical Gazette (англ.)русск. : journal. — 2019. — July (vol. 103, no. 557). — P. 222—232. — doi:10.1017/mag.2019.53.
- ↑ Fraivert, David. New applications of method of complex numbers in the geometry of cyclic quadrilaterals (англ.) // International Journal of Geometry : journal. — 2018. — Vol. 7, no. 1. — P. 5—16.
- ↑ Durell, Robson, 2003, с. 24.
- ↑ Peter, 2003, с. 315–6.
- ↑ 1 2 Coxeter, Greitzer, 1967, с. 57, 60.
- ↑ 1 2 Johnson, 2007, с. 84.
- ↑ 1 2 3 Durell, Robson, 2003, с. 26.
- ↑ Prasolov, 2006, с. 86, Задача 4.44.
- ↑ Alsina, Nelsen, 2009, с. 64.
- ↑ 1 2 Durell, Robson, 2003, с. 25,.
- ↑ 1 2 3 Alsina, Nelsen, 2007, с. 147–9.
- ↑ Crux, 2007, с. 123, # 2975.
