Какими свойствами обладают операции над событиями
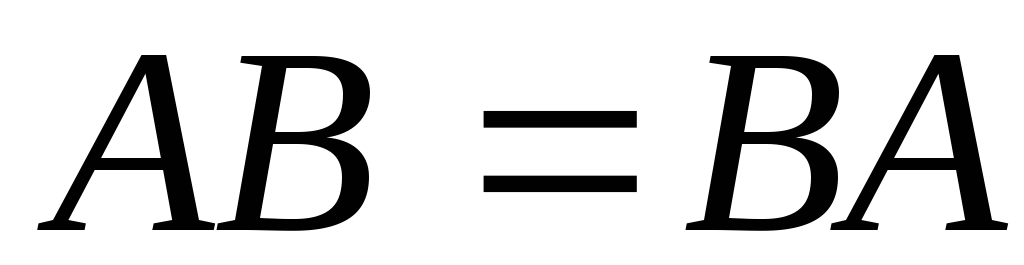
Некоторые свойства
операций над событиями постулируются,
другие легко могут быть получены с
помощью диаграмм Венна. Приведем без
доказательства основные из этих свойств.
Алгебра и сигма-алгебра событий.
Пусть
![]() является пространством всех элементарных
является пространством всех элементарных
исходов для какого-нибудь случайного
эксперимента, каждому результату
которого соответствует ровно одна точка![]() .
.
Выделим совокупность подмножеств![]() множества
множества![]() .
.
При этом потребуем, чтобы![]() содержало как случайные события
содержало как случайные события![]() ,
,
так и события, полученные в результате
применения любой из описанных операций
к любым элементам системы.
Совокупность
![]() случайных событий
случайных событий![]() (подмножеств множества
(подмножеств множества![]() ),
),
определенных на пространстве элементарных
исходов![]() ,
,
называетсяалгеброй событий (илибулевой алгеброй– по имени
английского математика Дж. Буля (1815 –
1864)), если выполнены следующие условия:
 ;
;Если
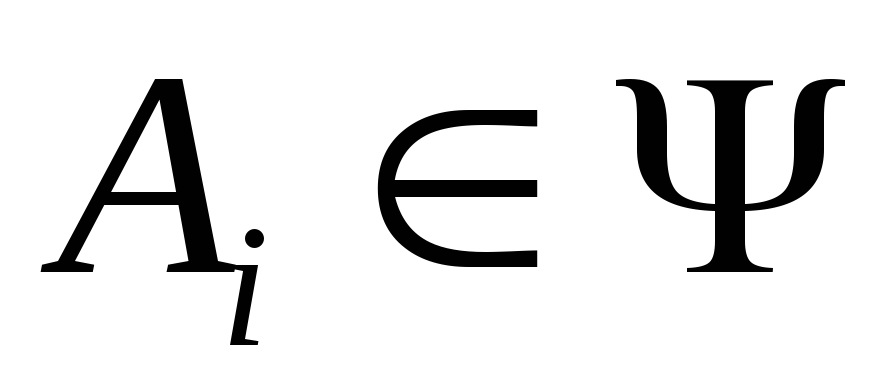 и
и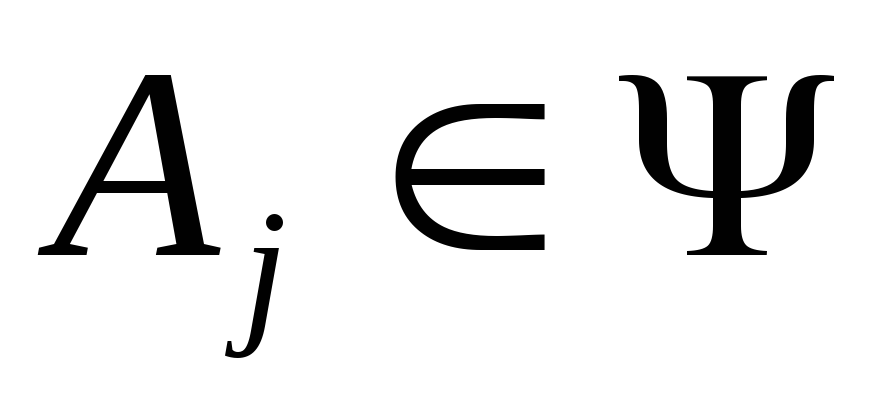 ,
,
то для
для
любых и
и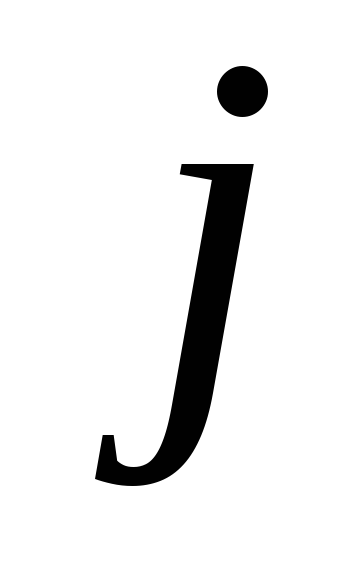 ;
;Если
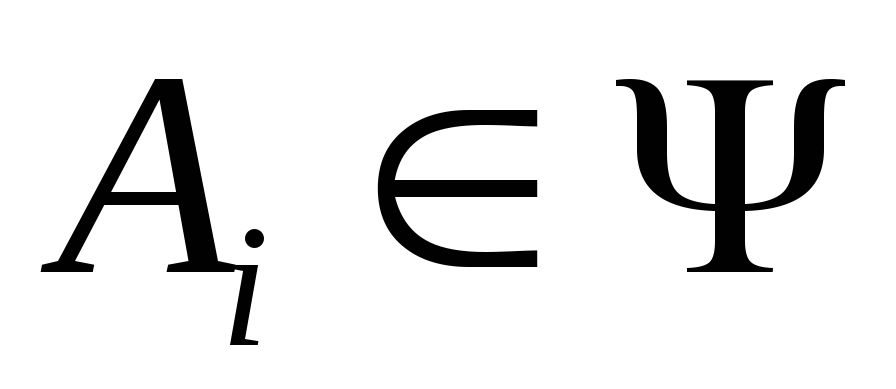 ,
,
то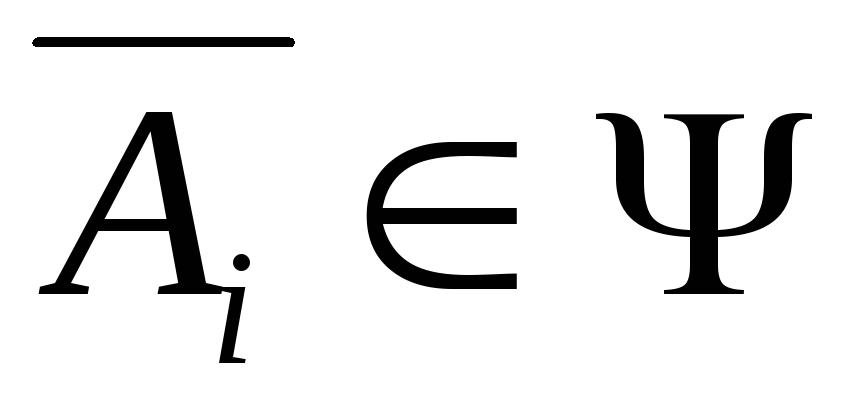 .
.
Оказывается, что
условий 1 – 3 достаточно для того, чтобы
любое конечное число других операций
над случайными событиями
![]() не выводило бы нас за пределы алгебры
не выводило бы нас за пределы алгебры![]() .
.
Для экспериментовс конечным числом
исходов множество всех подмножеств![]() ,
,
включающее пустое множество,
составляет алгебру. Поэтому для таких
экспериментов любое подмножество
множества![]() может интерпретироваться как наблюдаемое
может интерпретироваться как наблюдаемое
событие.
Во многих задачах
теории вероятностей приходится иметь
дело и с бесконечным числом элементарных
исходов и, следовательно, операций. Это
потребовало введения понятия -алгебры
событий.
Система подмножеств
![]() множества, называется-алгеброй,
множества, называется-алгеброй,
если она удовлетворяет следующим
условиям:
 ;
;Если
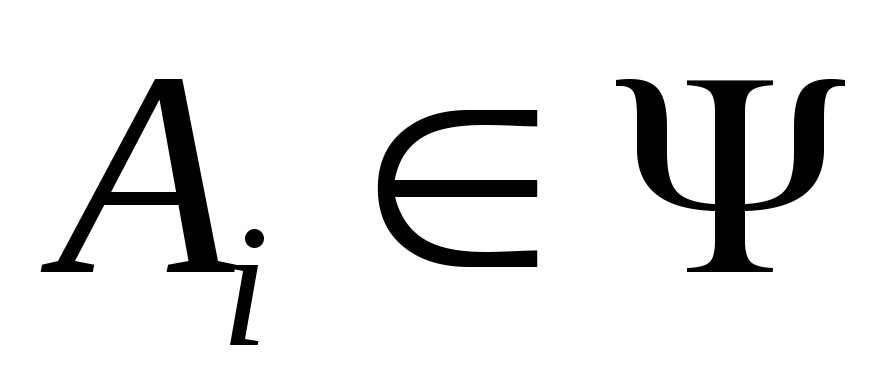 , то
, то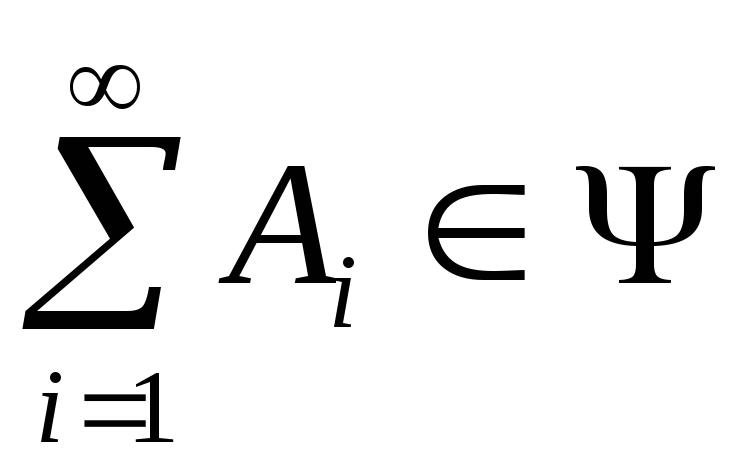 и
и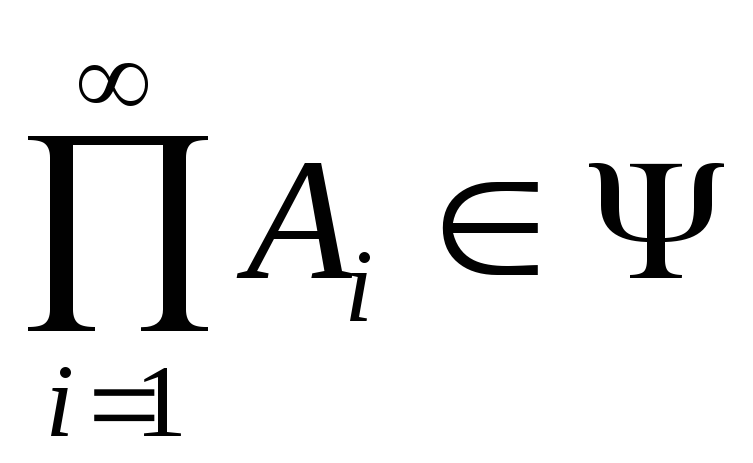
Если
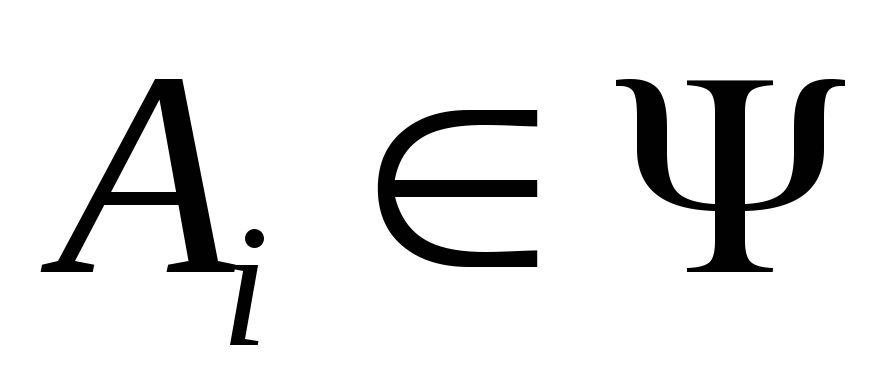 ,
,
то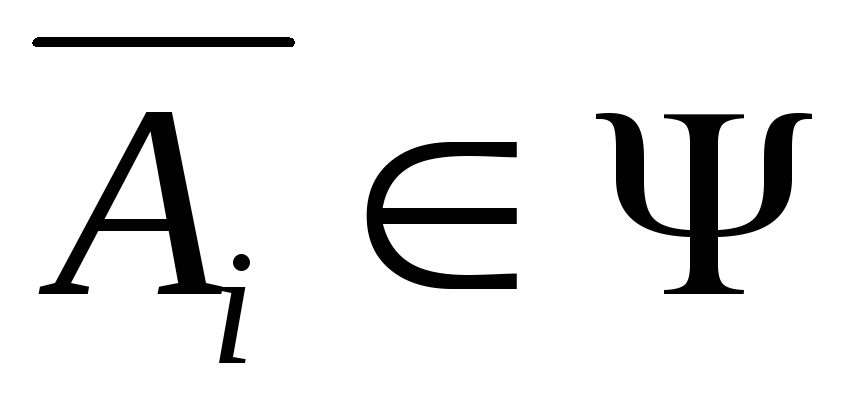 .
.
Таким образом,
счетное число операций суммирования
или перемножения событий не выводит
результирующее событие за пределы
–алгебры.
Лекция 3.
Классическое определение вероятности
события. Статистическое определение
вероятности. Геометрические вероятности.
Аксиоматическое построение теории
вероятностей. Вероятностное пространство.
Вероятностьявляется количественной мерой возможности
появления события. Наиболее широкое
распространение получили два определения
вероятности события: классическое и
статистическое.
Классическое определение вероятности события. Случаи равновероятных исходов.
Классическое
определение вероятностисвязано с
определением благоприятствующего
исхода. Исход называется благоприятствующим
данному событию, если его появление
влечет за собой наступление этого
события.Вероятность события равна
отношению числа равновозможных
благоприятствующих элементарных исходов
к общему числу всех равновозможных
элементарных исходов данного испытания:
![]() ,
,
где ![]() –
–
число благоприятствующих событию![]() исходов;
исходов;
![]() – общее число возможных исходов.
– общее число возможных исходов.
Примеры:1. Кубик,
2. Какова вероятность того, что в
произвольном двузначном числе две цифры
одинаковы (9/90 = 0.1), 3. Из букв слова
“дифференциал” выбирается одна буква.
Какова вероятность того, что это а)
гласная, б) буква “ф”.
Из определения
вероятности события
![]() следует, что
следует, что![]() ,
,
поэтому всегда выполняются неравенства![]() ,
,
т.е.вероятность любого события есть
неотрицательное число, не превышающее
единицы.
Если
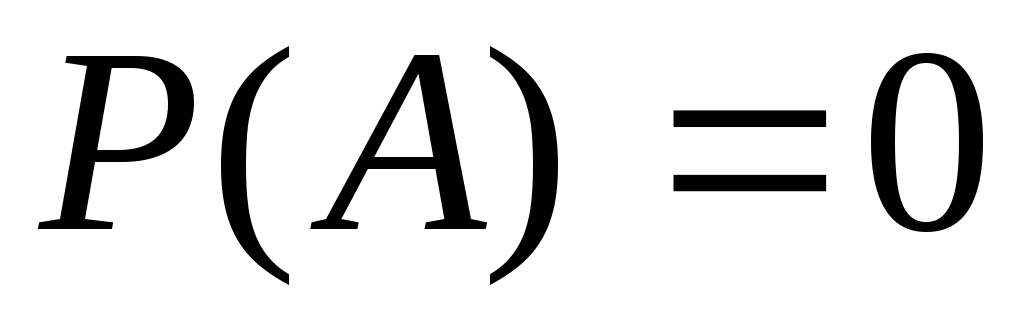 ,
,
то событие невозможное.
невозможное.Если
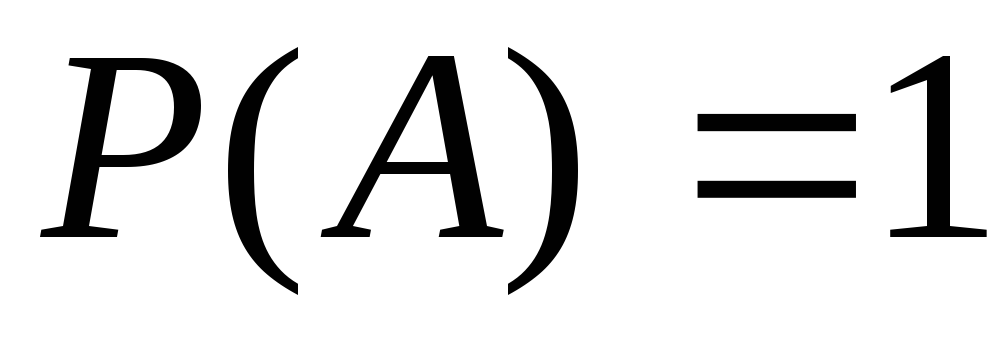 ,
,
то событие достоверное.
достоверное.Равновозможные
элементарные события являются
равновероятными, т.е. обладают одной
и той же вероятностью.
Теорема.
Эквивалентные события имеют
одинаковые вероятности, т.е. если
![]() ,
,
то![]() .
.
Доказательство.
Действительно, каждый элементарный
исход события![]() является таким же элементарным исходом
является таким же элементарным исходом
для события![]() и наоборот. В силу формулы
и наоборот. В силу формулы![]() справедливо равенство
справедливо равенство
![]() .
.
Если событие
![]() происходит всякий раз после того, как
происходит всякий раз после того, как
произошло событие![]() ,
,
то говорят, что из события![]() следует событие
следует событие![]() (
(![]() ).
).
Например, для любых двух событий![]() и
и![]() справедливо
справедливо![]() и
и![]() .
.
Теорема. Если
![]() ,
,
то![]() .
.
Доказательство.
Пусть![]() и
и![]() – число благоприятных элементарных
– число благоприятных элементарных
исходов соответственно для событий![]() и
и![]() ,
,
а![]() – общее число элементарных исходов.
– общее число элементарных исходов.
Так как каждый элементарный исход для
события![]() является также элементарным исходом
является также элементарным исходом
для события![]() ,
,
то![]() и, следовательно,
и, следовательно,![]() .Пример: выпадение четного числа
.Пример: выпадение четного числа
очков более вероятно, чем выпадение
двойки.
Теорема. Вероятность
события ![]() ,
,
противоположного событию ![]()
равна
![]() .
.
Доказательство.
Пусть полная система равновозможных
элементарных исходов содержит![]() событий, из которых
событий, из которых![]() (
(![]() ),
),
благоприятны событию![]() .
.
Тогда![]() исходов неблагоприятны событию
исходов неблагоприятны событию![]() ,
,
т.е. благоприятствуют событию![]() .
.
Таким образом,
![]() .
.
Классическое
определение вероятности предполагает,
что
число элементарных
исходов конечно;эти исходы
равновозможны.
Однако на практике
встречаются испытания с бесконечным
числом возможных исходов. Кроме того,
нет общих методов, позволяющих результат
испытания, даже с конечным числом
исходов, представить в виде суммы
равновозможных элементарных исходов.
Поэтому применение классического
определения вероятности весьма
ограничено. Пример: кубик со
смещенным центром тяжести.
Литература
1. А.А. Боровков, Курс теории вероятностей, Москва, Наука, 1972.
2. Б.В. Гнеденко, Курс теории вероятностей, Москва, Наука, 1961.
3. Ю.В. Прохоров, Ю.А. Розанов, Теория вероятностей, Москва, Наука, 1987.
4. В.С. Вентцель, Теория вероятностей, Москва, Высшая школа, 1998.
5. И.Н. Коваленко, А.А. Филиппова. Курс теории вероятностей и математическая статистика, Москва, Высшая школа, 1982.
6. Коломиец Э.И., Дегтярев А.А. Сборник задач по теории вероятностей, Учебное пособие, 2006
План лекции
1.Случайный эксперимент, случайные события
2. Операции над событиями
3. Статистическое определение вероятности.
4. Классическое определение вероятности. Комбинаторные формулы.
5. Геометрические вероятности.
6. Свойства вероятности.
Т.В. изучает так называемые случайные события и устанавливает закономерности в проявлении таких событий.
Для введения понятия случайного события рассмотрим некоторые примеры реальных экспериментов.
1. Производится бросание монеты, результатом данного эксперимента могут быть два исхода; выпадение герба или решетки.
2. Из колоды 36 карт наудачу выбирают карту. Имеется 36 возможных исходов, которые можно закодировать числами 1,…,36.
3. Ставят на испытание n изделий. Через время Т испытание прекращают и фиксируют, какие изделия вышли из строя. Исходы эксперимента – n-мерные булевы векторы , где , если i-ое изделие вышло из строя и в противном случае.
4. Ставят на испытание n изделий. Испытание во времени не ограничивают; для каждого i измеряют время ti отказа i-го изделия. Исходы эксперимента – n-мерные векторы с неотрицательными компонентами.
5. Производят стрельбу по мишени. Связав с мишенью декартову систему координат, можно отождествить с любым исходом испытания точку (x,y) координатной плоскости.
6. Датчик записывает температурный режим в плавильной печи за время Т плавки. Исходом этого испытания является функция .
Попытаемся найти общие черты приведенных примеров реальных испытаний.
1) В каждом испытании имеется определенное пространство возможных исходов испытания, называемых элементарными исходами.
В примере 1: ,
в примере 2: ,
в примере 3: ,
в примере 4: ,
в примере 5: ,
в примере 6: есть множество непрерывных функций на отрезке [0,T].
2) Исходы испытания не детерминированы.
3) Существует объективная мера возможности различных исходов испытаний.
Множество всех возможных элементарных исходов испытания будем называть пространством элементарных событий.
Введем понятие случайного события А, как подмножества пространства элементарных событий . Событие происходит в каждом испытании и его будем называть достоверным. Событие никогда не происходит и его будем называть невозможным.
Определив события в терминах теории множеств, мы можем ввести для событий обычные операции теории множеств, которые для событий имеют свой смысл:
1. или — пересечение множеств А и В, соответствует случаю когда в опыте происходят события А и В. События А и В называются несовместными, если .
2. или — объединение множеств А и В, соответствует случаю когда в опыте происходит хотя бы одно из событий А, В.
3. — событие, включающее все не входящие в А и только их. Событие называется противоположным к А событием и соответствует случаю, когда в опыте событие А не происходит.
4. или — событие, включающее все , которые принадлежат А и не принадлежат В. Событие называется разностью событий А и В и соответствует случаю, когда в опыте событие А происходит, а событие В — нет. Легко видеть, что .
5. Симметрической разностью событий A и B называется событие .
6. Для событий можно определить также отношение следования: . Это означает, что если в опыте происходит событие А, то обязательно происходит и событие В (событие А влечет событие В).
A+B AB
A–B
Рис. 1. Операции над событиями (результат – заштрихованная область)
Пример.
Рассмотрим опыт с бросанием 2-х игральных костей.
В данном случае пространство элементарных событий соответствует множеству пар чисел (i,j), где i -число очков, выпавших на 1-ой кости, а j – на второй; .
Введем события А – выпадает четная сумма очков, А1 – на каждой грани выпадает четное число очков, А2 – на каждой грани выпадает нечетное число очков.
Легко видеть, что
,
.
События обозначают: выпадает нечетная сумма очков, хотя бы на одной грани выпадает нечетное число очков, хотя бы на одной грани выпадает четное число очков.
Используя формулу , получим
Действительно, рассмотрим первое из вышеприведенных выражений: .
означает, что «хотя бы на одной грани выпадает нечетное число очков» и «выпадает нечетная сумма», что возможно только когда на «на каждой грани выпадает нечетное число очков», то есть .
Основные свойства операций над событиями
1. А+В=В+А, АВ=ВА — коммутативность
2. А+(В+С)=(А+В)+С=А+В+С,
А(ВС)=А(ВС)=АВС — ассоциативность
3. А(В+С)=АС+ВС – дистрибутивность
4. А+А=А, АА=А
5.
6.
7.
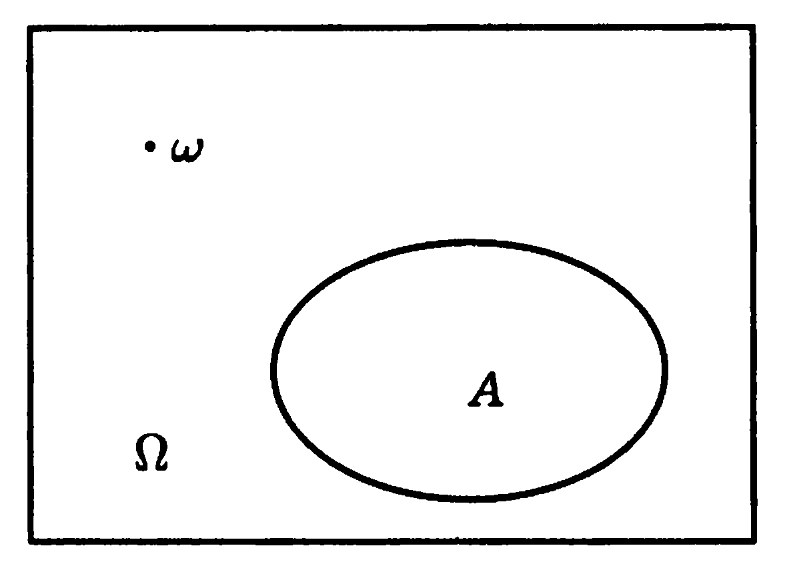
Рис. 1. Изображение диаграммы
Эйлера-Венна
Часто бывает полезно наглядно представить события в виде диаграммы Эйлера — Венна. Изобразим все пространство элементарных исходов прямоугольником (рис. 1). При этом, каждый элементарный исход %%omega%% соответствует точке внутри прямоугольника, а каждое событие %%A%% — некоторому множеству точек, этого прямоугольника.
Рассмотрим теперь операции над событиями, которые совпадают с операциями над множествами.
Определение
Пересечением (произведением) двух событий %%A%% и %%B%% называют событие, обозначаемое %%A cap B%% или %%AB%%, происходящее тогда и только тогда, когда одновременно происходят оба события %%A%% и %%B%%, т.е. событие, состоящее из тех и только тех элементарных исходов, которые принадлежат и событию %%A%%, и событию %%B%%.
События %%A%% и %%B%% называются несовместными, или непересекающимися, если их пересечение является невозможным событием, т.е. если %%A cap B = varnothing%%.
В противном случае события называют совместными, или пересекающимися.
Определение
Объединением (суммой) двух событий %%A%% и %%B%% называют событие, обозначаемое %%A cup B%%, происходящее тогда и только тогда, когда происходит хотя бы одно из событий %%A%% или %%B%%, т.е. событие состоит из элементарных исходов, которые принадлежат хотя бы одному из множеств %%A%% или %%B%%.
Если события %%A%% и %%B%% несовместимы, то для обозначения могут использововать символ «%%+%%».
Например, поскольку невозможное событие %%varnothing%% несовместно с любым событием %%A%%, то
$$
varnothing cup A = varnothing + A = A.
$$
Аналогично определяют понятия произведения и суммы событий для любого конечного числа событий и даже для бесконечных последовательностей событий. Так, событие
$$
A_1 A_2 ldots A_n = bigcap_{i = 1}^n A_i
$$
состоит из элементарных исходов, принадлежащих всем событиям %%A_i, i = overline{1,n}%%, а событие
$$
A_1 cup A_2 cup ldots cup A_n = bigcup_{i = 1}^n A_i
$$
состоит из элементарных исходов, принадлежащих хотя бы одному из событий %%A_i, i = overline{1,n}%%.
В частности, события %%A_1, A_2, ldots, A_n%% называют попарно несовместными, если
$$
A_i A_j = varnothing
$$
для любых %%i,j = overline{1,n}, i neq j%%, и несовместными в совокупности, если
$$
A_1 A_2 ldots A_n = varnothing.
$$
Определение
Разностью двух событий %%A%% и %%B%% называют событие, обозначаемое %% A setminus B%%, происходящее тогда и только тогда, когда происходит событие %%A%% и не происходит событие %%B%%, т.е. состоит из тех элементарных исходов, которые принадлежат событию %%A%% и не принадлежат событию %%B%%
Определение
Дополнением события %%A%% называют новое событие, обозначаемое %%overline{A}%%, происходящее тогда и только тогда, когда не происходит событие %%A%%. Так событие %%overline{A}%% можно записать в виде:
$$
overline{A} = Omega setminus A.
$$
Событие %%overline{A}%% называют событием, противоположным событию %%A%%.
Определение
Событие %%A%% включено в событие %%B%%, если появление за собой события %%A%% обязательно влечет за собой наступление события %%B%%, или каждый элементарный исход события %%A%% принадлежит и событию %%B%%.
Приоритеты операций
Если некоторое событие записано в виде нескольких операций над различными событиями, то сначала выполняется операция дополнения, затем умножения, и, наконец, сложение и вычитание (слева направо).
Скобки могут увеличить приоритет любой из операций.
Пример
Рассмотрим устройство из %%n%% элементов. Элементы соединены последовательно, если устройство прекращает функционировать при отказе любого из элементов, и соединены параллельно, если прекращение функционирования наступает только при отказе %%n%% элементов (рис. 1а, 1б соответственно).
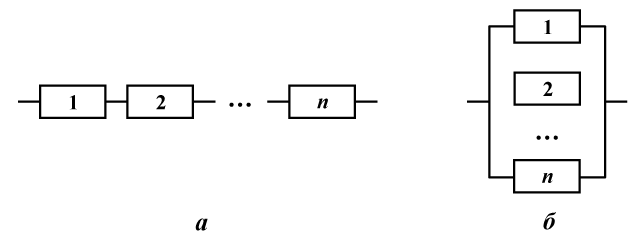
Рис 1. Последовательное и параллельное соединения
Обозначим %%A%% событие, означающее отказ системы, а %%A_i%% — отказ %%i%%-го элемента (%%i = overline{1,n}%%). Тогда для последовательного соединения событие %%A%% представимо в виде:
$$
A = A_1 cup A_2 cup ldots A_n,
$$
а для параллельного соединения
$$
A = A_1 cap A_2 cap ldots A_n.
$$
Очевидно, что при параллельном соединении элементов событие %%A%% включено в каждое из событий %%A_i, i = overline{1,n}%%, а при последовательном соединении любое событие %%A_i, i = overline{1,n}%% включено в событие %%A%%.
Три действия: формирование противоположного события, сложение и умножение событий составляют алгебру событий, а их свойства, перечисленные в табл. 1, — законыалгебры событий. Законы под номером 1 называются коммутативными, 2 – ассоциативными, 3 – дистрибутивными, 10 — законами де Моргана[2].
Для нескольких операндов свойство дистрибутивности умножения относительно сложения и сложения относительно умножения имеет вид
, (9)
(10)
а законы де Морганапредставляются следующими соотношениями
, . (11)
Примечательно, что третий столбец табл. 1 можно получить из второго заменой операции сложения на операцию умножения событий с одновременной заменой достоверного события на невозможное и невозможного события на достоверное. Таким же образом получается второй столбец из третьего. Это свойство законов алгебры событий называется принципом двойственности.
Для количественной оценки возможности осуществления событий используют функцию вероятности. Аргументом этой функции является событие, а ее значение – неотрицательное число. Функция вероятности может быть определена на основе следующих подходов:
1. определение вероятности на основе элементарного понятия равновозможности (классическое определение вероятности);
2. определение вероятности как доли длины, площади, объема и т.д. (геометрическое определение вероятности);
3. аксиоматическое определение вероятности;
4. определение вероятности как частоты появления события при большом количестве испытаний (статистическое определение вероятности).
Перейдем теперь к рассмотрению способов определения вероятности событий.
Контрольные вопросы
1. Что такое событие?
2. Что такое достоверное событие?
3. Что такое невозможное событие?
4. Дайте определение операции сложения двух событий.
5. Дайте определение операции умножения двух событий.
6. Дайте определение операции вычисления разности двух событий.
7. Дайте определение операции образования противоположного события.
8. Какие события называются несовместными, а какие совместными?
9. Что означает утверждение «событие А раскладывается на частные случаи В1, В2, …, Вп »?
10. В каком случае события образуют полную группу событий?
11. Охарактеризуйте множество событий, составляющих поле событий.
2. Вычисление вероятностей
2.1. Классическое определение вероятности событий
1.1. Классическая схема испытаний
Предположим, что в результате испытания происходит только одно из элементарных равновозможныхсобытий . Это означает, что достоверное событие составляет сумма
, (1)
где , если (в одном испытании не может быть двух разных исходов).
События называют также результатами испытаний. Множество элементарных событий обозначим тем же символом , которым обозначалось достоверное событие.
Понятие равновозможности является основополагающим и не выводится из каких-либо других понятий. Вероятность осуществления каждого из этих элементарных событий считается одинаковой и принимается равной
. (2)
С учетом определения (2) события множества называются также равновероятными. На основе множества элементарных событий образуем поле событий , применяя к элементарным событиям множества операции формирования противоположного события, сложения и произведения событий.
Пусть событие представляется суммой элементарных событий из множества
, (3)
где индексы , т.е. каждое событие является одним из элементарных событий. Элементарные события, составляющие сумму (3), называют результатами испытаний, благоприятствующими событию . Число таких событий обозначим символом . Тогда вероятность события вычисляется по формуле
. (4)
Пример (на классическое вычисление вероятности).
Определить вероятность выпадения четного числа очков при бросании игральной кости.
При бросании игральной кости, возможны 6 (n=6) равновероятных исходов: , где индекс символа испытания указывает выпавшее число. Событие выпадения четного числа очков представляется суммой трех элементарных событий (m=3)
.
Таким образом .
1.2. Свойства функции вероятности, определенной по классической схеме
Вероятность, определенная по формуле (1.1.4) обладает следующими свойствами.
1. Для каждого события поля
. (1)
2. Для достоверного события
. (2)
3. Если событие подразделяется на частные случаи и (т.е. ), то
. (3)
Первые два свойства очевидны. Докажем третье.
Доказательство
Пусть — число элементарных событий, благоприятствующих событию , — число элементарных событий, благоприятствующих событию , — число всех элементарных событий.
Поскольку события и несовместны, то не существует событий одновременно благоприятствующих и , и . Это значит, что число событий, благоприятствующих или или равно , т.е.
, n
Свойство (3) иногда формулируется как теорема сложения вероятностей.
4. Вероятность события , противоположного , равна
. (4)
Доказательство
Так как
и ,
то
.
Следовательно,
. n
5. Вероятность невозможного события равна 0, т.е.
. (5)
Доказательство
Так, как
и ,
то
.
Следовательно,
. n
6. Если событие влечет за собой событие , т.е.
, то . (6)
Доказательство
Пусть — число элементарных событий, благоприятствующих событию , а — число элементарных событий, благоприятствующих событию . В число входят события, составляющие число , но возможно еще какие-либо. Поэтому . Следовательно, или [3]. n
7. Вероятность любого события заключена между нулем и единицей
. (7)
Доказательство
Так, как , то . n
Заменяя в последнем соотношении и на 0 и 1 соответственно (см. формулы (5) и (2)), получим соотношение (7).n
При решении задач, связанных с вычислением классической вероятности, бывает необходимым использование понятий и формул комбинаторики. Перейдем к рассмотрению основных понятий комбинаторики: перестановка, сочетание и размещение.
Контрольные вопросы
1. В чем состоит классический способ вычисления вероятности событий?
2. Чему равна вероятность невозможного события?
3. Чему равна вероятность достоверного события?
4. Как выразить вероятность суммы двух несовместных событий, используя вероятности каждого из них в отдельности?
5. Как связаны вероятности двух взаимно противоположных событий?
2. Элементы комбинаторики
2.1. Перестановки
Пусть рассматривается n различных символов. Их запись, например, через запятую называется перестановкой. Каждому символу в перестановке можно сопоставить его порядковый номер в ней, начиная с первого. Две перестановки из одного и того же числа одинаковых символов называются одинаковыми, если каждый из n символов занимает положение в перестановке с одним и тем же номером (одно и то же место). В противном случае, перестановки считаются различными.
Какое число различных перестановок можно получить, изменяя места расположения символов? Для ответа на этот вопрос приведем следующие рассуждения. Имея различных символов можно на первое место поставить по очереди каждый из них в отдельности. В этом случае образуется различных групп перестановок. Каждая такая группа перестановок имеет одну и ту же черту — одинаковый символ, стоящий на первом месте. После фиксации положения одного символа на первом месте на второе место можно поставить любой из оставшихся символов, что составляет возможность. Последовательность этих рассуждений можно продолжить до тех пор, пока не будут зафиксированы символов, и последний оставшийся можно будет расположить только единственным способом на месте с номером . Таким образом, общее число возможных перестановок n различных символов составляет
. (1)
Пример. Сколькими способами можно расставить на полке 10 книг?
Решение. Существует различных способов расстановки 10 книг на полке.
Контрольные вопросы
1. Что такое перестановка из различных элементов?
2. Какие две перестановки считаются различными?
3. Как вычислить максимальное число различных перестановок из различных элементов?
2.2. Сочетания
Рассмотрим те же различных символов (элементов[4]). Однако сейчас их взаимное расположение не является существенным. Т.е. эти символы рассматриваются как элементы множества. Пусть из множества, состоящего из символов, требуется сформировать подмножества из меньшего числа тех же символов. Каждое из таких подмножеств называется сочетаниемиз элементов по и их количество обозначается как . Сколько различных таких подмножеств можно составить? Два сочетания считаются различными, если они состоят или из разного количества элементов или если в состав одного из них входит хотя бы один элемент, отсутствующий во втором.
Теорема
. (1)
Доказательство
Применим метод математической индукции. Число сочетаний из элементов по , очевидно, равно , т.е. . Непосредственной подстановкой можно проверить, что в этом случае формула (1) выполняется. Предположим, что формула (1) выполняется вплоть до некоторого значения . Покажем ее справедливость при . Рассмотрим произвольное сочетание из множества . Его можно дополнить до сочетания из элементов по всего способами. Эту операцию можно осуществить со всеми сочетаниями из числа . Таким образом можно получить сочетания из элементов по элементу в каждом способами. Среди этих сочетаний, состоящих из элементов, будут встречаться одинаковые. В силу симметрии число одинаковых сочетаний для каждого типа сочетаний будет одним и тем же. Подсчитаем число повторяющихся сочетаний. Для сочетания определенного типа выберем мысленно одно из вновь образованных сочетаний с элементами. Сочетания с элементами, на основе которых будут получены такие же новые сочетания с элементами, могут быть получены поочередным выкидываем одного элемента. Легко сообразить, что их число составит . Таким образом, число различных сочетаний из элементов по составит
. n
Пример 1. (на методику формирования поля событий ).
Пусть группа равновероятных исходов испытаний состоит из трех событий . Поле событий состоит из следующих восьми элементов: , , , , , . Подсчет количества элементов поля событий осуществляется по формуле
.
Заменяя первые два слагаемых последнего равенства сочетаниями, получаем
,
где и .
Очевидно, что для случая событий поле событий включает в себя элементов, так как справедливо следующее равенство
(2)
Пример 2. Среди 100 фотографий есть одна разыскиваемого преступника. Наудачу выбирают 10 фотографий. Какое количество сочетаний по 10 фотографий, содержащих фотографию разыскиваемого преступника, существует?
Решение. Если убрать одну фотографию преступника, то останется 99 фотографий. Составим всевозможные сочетания из 99 фотографий по 9 в каждом и добавим к каждому сочетанию фотографию преступника. В результате получим искомое множество. Таким образом, всего существует сочетаний.
Контрольные вопросы
1. Что такое сочетание из п различных элементов, содержащее элементов?
2. Какие два сочетания считаются различными?
3. Как определить максимальное число различных сочетаний из п различных элементов по т элементов в каждом?
4. Как определяется символ 0!?
2.3. Размещения
Определение. Любой упорядоченный набор различных элементов, взятых из множества, состоящего из элементов, называется размещением.
Для каждого из сочетаний существует различных размещений. Следовательно, число размещений из элементов по составляет
. (1)
Пример. В соревновании участвуют 8 команд. Какое количество различных способов распределения первых трех мест существует?
Решение. .
Контрольные вопросы
1. Что такое размещение из различных элементов, содержащее элементов?
2. Какие два размещения считаются различными?
3. Как вычислить максимальное число различных размещений из различных элементов по элементов в каждом?
2.4. Формула Стирлинга
Для приближенного вычисления факториала в случае больших значений аргумента используется формула Стирлинга[5][10]
. (1)
2.5. Формула бинома Ньютона
Примечательно, что числа сочетаний из элементов по являются коэффициентами в формуле бинома Ньютона[9]
. (1)
При этом так как , то
. (2)
§ 3. Геометрическое определение вероятности событий
Во многих случаях применение классического способа вычисления вероятности оказывается невозможным по причине бесконечного числа возможных исходов испытаний. Например, пусть в результате испытания внутри круга радиусом размещается точка (см. рис. 1). Предположим, что вероятность попадания точки в область Ц, составляющую часть круга, не зависит от формы и положения этой области, а зависит только от ее площади. Тогда естественно определить вероятность попадания точки в область Ц как
, (1)
где — площадь области Ц.
Рис. 1. Геометрический способ вычисления вероятности
Аналогичная ситуация возникает в задаче о встрече. Два человека договорились встретиться в определенном месте между 12 часами и часом. Человек, пришедший первым, ждет другого 20 минут и уходит. Чему равна вероятность их встречи, если приход каждого из них в течение указанного часа происходит случайно и моменты прихода независимы.
Решение
Пусть — время прихода лица , — время прихода лица . Встреча состоится, если
. (2)
Представим задачу графически в Декартовой системе координат, в которой по оси Х отложим время х прихода лица А, а по оси Y – время y прихода лица В (рис. 2).
Приход лиц и в назначенное место встречи описывается случайной точкой в квадрате на указанной плоскости со стороной 60 мин. Событие «встреча» соответствует попаданию точки в область, определяемую неравенством (2). Более подробно это неравенство можно записать в виде:
если , то
или
если , то .
Эта область на рисунке заштрихована.
Рис. 2. Геометрический способ вычисления вероятности в задаче о встрече
Вероятность встречи можно вычислить как отношение площади заштрихованной области к площади квадрата, т.е.
.
Приведенные примеры можно использовать при решении задач, в которых целесообразно применение геометрического способа вычисления вероятности.
Контрольные вопросы
1. В чем состоит геометрический способ выч?
