Какими свойствами обладает свойство умножения дробей

В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
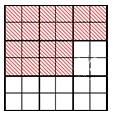
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a — b) = m · a — m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a — b) · m = a · m — b · m.
Переход от умножения:
m · (a + b) и m · (a — b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a — m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a — m · b
к умножению:
m · (a + b) и m · (a — b)
называется вынесением общего множителя за скобки.
Дата:
19.11.2016 год.
Классы:
6 «А,Б,В,Г,Д»
Тема и номе урока:
«Умножение дробей» (П.13), урок №4
Тип урока
урок совершенствования знаний, умений и навыков.
Оборудование
доска, тетради, карточки с заданиями, мел, смайлики, презентация.
Цель урока:
Отработать знания, умения и навыки по теме:
«Умножение обыкновенных дробей».
Задачи:
Образовательные:
Повторить и закрепить правила умножения обыкновенных дробей, умножение смешанных чисел, умножение обыкновенной дроби на натуральное число;
Продолжить формирование умений пользоваться данными правилами в различных ситуациях
Развивающие:
Развитие познавательных интересов учащихся;
Развитие логического мышления учащихся;
Развитие навыков самостоятельной работы.
Воспитательные:
Воспитание коммуникативных качеств личности, навыков самоконтроля, взаимоконтроля.
Ход урока
1. Организационный момент.
Здравствуйте, садитесь. Очередной урок посвящен умножению дробей. Сегодня мы обобщим знания по этой теме и покажем, как умеем их применять.
2. Проверка Д/З
П.13,№475
Устная работа.
1. Учитель раздаёт карточки. На них написаны числа:
184, 200, 345, 720
—Выбрать числа, которые делятся и на 2, и на 5.
-Вспомним, какие числа делятся на 3, на 9?
2.Выполните умножение:
а)
3. Решите уравнение:
1) х+8х + 2 = 5
2) 6х – х + 5 = 14
Повторение пройденного материала.
1. Что такое числитель?
2. Что такое знаменатель?
3. Какая дробь называется правильной?
4. Какая дробь называется неправильной?
5. В чем заключается основное свойство дроби?
6. Как сокращают дроби?
7. Какую дробь называют несократимой?
8.Как сложить (или вычесть) дроби с разными знаменателями?
9. Как выделить из неправильной дроби целую часть?
10. Как представить смешанное число в виде неправильной дроби?
11. Как умножить дробь на натуральное число?
12 Запишите свойства нуля и единицы при умножении.
Изучение нового материала
— Как называются дроби, которые меньше 1? (Правильные дроби.)
— Как называются дроби, которые больше 1? (Неправильные дроби.)
— Найдите значение выражения:
— Какими свойствами обладает действие умножения дробей?
Вспомните свойства умножения для натуральных чисел. Запишите их с помощью буквенных обозначений.
Запись в тетрадях:
1) Переместительное свойство умножения а · b = b · а
2) Сочетательное свойство умножения (а · b) · с = а · (b · с)
3) Свойство нуля а · 0 = 0 · а = 0
4) Свойство единицы а · 1 = 1 · а = а а ·
5) Если а ≠ 0
6) Распределительное свойство умножения относительно сложения
(a + b) · c = a · c + b · c
7) Распределительное свойство умножения относительно вычитания
(а — b) · с = а · с – b · с
— Для чего используют свойства умножения? (Для упрощения вычислений)
— Эти свойства справедливы и для дробных чисел.
— Приведите примеры, подтверждающие эти свойства для дробей.
Работа по учебнику.
№ 446 (н-п) стр. 73 (самостоятельно, устная проверка).
(Ответ: н) 0; о) ; п) 0.)
2. На какое число надо умножить число 5, чтобы произведение было:
1) равно 0; 2) равно 1; 3) равно 5; 4) больше 5; 5) меньше 5.
№454.Найдите значение выражения:

Физкультминутка
Подтянулись на носочках
Столько раз,
Ровно столько, сколько пальцев
На руке у вас!
1, 2, 3, 4, 5!
Топаем ногами,
1, 2, 3, 4, 5!
Хлопаем руками.
Работа над задачей
№ 450 стр. 73 (после разбора самостоятельно, самопроверка, образец на обратной стороне доски).
— Прочитайте задачу.
— Как двигались два велосипедиста? (В одном направлении.)
— Зная скорость первого велосипедиста и то, что скорость второго в 1 раза больше, что можно найти? (Скорость второго велосипедиста.)
— Как найти скорость второго велосипедиста? (Скорость первого велосипедиста умножить на 1
— Зная скорости двух велосипедистов, что можно найти? (Скорость удаления.)
— Как найти скорость удаления?
(Из большей скорости вычесть меньшую скорость.)
— Зная скорость удаления и время, что можно найти?
(Расстояние, которое будет между двумя велосипедистами через 1 ч.)
Решение:

(Ответ: 3,06 км будет между ними через 1 ч.)
Самостоятельная работа (10—15 мин)
1. Найдите значение выражения:

2. На чтение первого рассказа Лена затратила 3/4 ч, а на чтение второго рассказа — в ![]() раза больше. Сколько времени Лена затратила на чтение двух рассказов? На сколько времени меньше у нее ушло на чтение первого рассказа, чем второго?
раза больше. Сколько времени Лена затратила на чтение двух рассказов? На сколько времени меньше у нее ушло на чтение первого рассказа, чем второго?
3. Выполните действия: 
Итог урока:
-Что вы узнали сегодня на уроке?
— Чему научились?
— Что более всего запомнилось на уроке?
Домашнее задание
П.13, 478. Выполните действия:

Рефлексия:
Графическая: на доске таблица со знаками

В таблице цели урока можно записать самому учителю В конце урока учащиеся плюсуют напротив каждой цели и в той графе, которую они считают более приемлемой.
__________/19.11.2016 год.
