Какими свойствами обладает медиана треугольника

Определение

Медиана – это отрезок, соединяющий высоту и середину противоположной стороны. В треугольнике три вершины, а значит и медианы три. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные отрезки.

Свойства медиан

• Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
• Все медианы треугольника пересекаются в одной точке.
• Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольника.

Равновеликими называют треугольники, площади которых равны.

Рис. 1. Три медианы образуют 6 равновеликих треугольника.

• Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
• Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.

Задачи

Все эти свойства несложно запомнить, они легко закрепляются на практике. Для большего понимания темы, решим несколько задач:

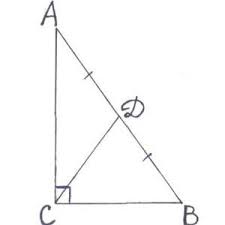
Рис. 2. Рисунок к задаче.

Для того, чтобы найти значение медианы, нам необходимо найти гипотенузу, так как медиана, проведенная к гипотенузе равна ее половине. Гипотенуза через теорему Пифагора: $$a^2+b^2=c^2$$

$$c=sqrt{a^2+b^2}=sqrt{9+16}=sqrt{25}=5$$

Найдем значение медианы: $$m={cover2}={5over2}=2,5$$ – получившееся число и есть значение медианы.

Рис. 3. Рисунок к задаче.

Чтобы решить эту задачу нужно воспользоваться одной из трех формул для нахождения медианы по сторонам треугольника:

$$m^2 ={1over2}*(a^2+c^2-b^2)$$

Как видно, главное здесь запомнить коэффициент при скобках и знаки у значения сторон. Знаки запомнить проще всего – вычитается всегда сторона, к которой опущена медиана. В нашем случае это b, но может быть любая другая.

Подставим значения в формулу и найдем величину медианы: $$m=sqrt{{1over2}*(a^2+c^2-b^2)}$$

$$m=sqrt{{1over2}*(49+81-64)}=sqrt{33}$$ – оставим результат в виде корня.

Медианы, разбивают треугольник на шесть равновеликих. Значит, площади малых треугольников будут равны между собой. Достаточно найти площадь большего и поделить ее на 6.

Дана медиана, проведенная к основанию, в равнобедренном треугольнике она является биссектрисой и высотой. Значит в треугольнике известны основание и высота. Можно найти площадь.

$$S={1over2}*6*8=24$$

Площадь каждого из малых треугольников: $${24over6}=4$$

Тест по теме

Определения

Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.

Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.

Теорема

Теорема

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.

[{Large{text{Медиана}}}]

Теорема

В любом треугольнике медианы точкой пересечения делятся в отношении (2:1), считая от вершины.

Доказательство

(DE) – средняя линия в треугольнике (ABC), тогда (DEparallel AB), значит (angle ADE = angle BAD), (angle BED = angle ABE), следовательно, треугольники (ABO) и (DOE) подобны (по двум углам).

Из подобия треугольников (ABO) и (DOE): (dfrac{BO}{OE} =
dfrac{AB}{DE} = dfrac{2}{1}).

Для других медиан треугольника (ABC) требуемое свойство доказывается аналогично.

Теорема

Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).

Доказательство

Пусть (BD) – медиана в треугольнике (ABC), тогда (AD = DC).

(S_{ABD} = 0,5cdot ADcdot h),

(S_{BCD} = 0,5cdot DCcdot h).

Так как (AD = DC), то (S_{ABD} = S_{BCD}), что и требовалось доказать.

Теорема

В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.

Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.

Доказательство

Достроим треугольник (ABC) до прямоугольника (ABCD) и проведем диагональ (BD). Т.к. в прямоугольнике диагонали делятся точкой пересечения пополам и равны, то (ACcap BD=M), причем (AM=MC=BM=MD), чтд.

Треугольники (AMB) и (CMB) – равнобедренные, следовательно, (angle
BAM=angle ABM=alpha, quad angle MBC=angle MCB=beta).

Т.к. сумма углов в треугольнике равна (180^circ), то для (triangle
ABC):

(alpha+(alpha+beta)+beta=180^circ Rightarrow
alpha+beta=90^circ Rightarrow angle B=90^circ), чтд.

[{Large{text{Биссектриса}}}]

Теорема

Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.

Доказательство

Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть [dfrac{S_{ACD}}{S_{BCD}} = dfrac{ACcdot CD}{CBcdot CD} =
dfrac{AC}{CB}]

С другой стороны, (dfrac{S_{ACD}}{S_{BCD}} = dfrac{0,5cdot
ADcdot h}{0,5cdot DBcdot h}), где (h) – высота, проведённая из точки (C), тогда (dfrac{S_{ACD}}{S_{BCD}} = dfrac{AD}{DB}).

В итоге (dfrac{AD}{DB} = dfrac{S_{ACD}}{S_{BCD}} =
dfrac{AC}{CB}), откуда (dfrac{AD}{AC} = dfrac{DB}{BC}), что и требовалось доказать.

Теорема

Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.

Доказательство

1) Докажем, что если (KA=KB), то (OK) – биссектриса.
Рассмотрим треугольники (AOK) и (BOK): они равны по катету и гипотенузе, следовательно, (angle AOK=angle BOK), чтд.

2) Докажем, что если (OK) – биссектриса, то (KA=KB).
Аналогично треугольники (AOK) и (BOK) равны по гипотенузе и острому углу, следовательно, (KA=KB), чтд.

У этого термина существуют и другие значения, см. Медиана.

Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.

Свойства

Основное свойство

Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.

Свойства медиан равнобедренного треугольника

• В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой.
• Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
• У равностороннего треугольника все три медианы равны.

Свойства оснований медиан

• Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
• Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
  • Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.

Другие свойства

• Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
• Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
• Треугольник делится тремя медианами на шесть равновеликих треугольников.
• Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
• В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
• Большей стороне треугольника соответствует меньшая медиана.
• Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
• Медиана угла треугольника изотомически сопряжена самой себе.

• Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).

Основные соотношения

• Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):

где  — медиана к стороне ; — стороны треугольника.В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:.

• Обратно, можно выразить длину произвольной стороны треугольника через медианы:

,где медианы к соответствующим сторонам треугольника,  — стороны треугольника.

• Площадь любого треугольника, выраженная через длины его медиан:

где  — полусумма длин медиан.

См. также

• Инцентр
• Симедиана
• Центроид
• Чевиана
• Биссектриса

Литература

• Ефремов Дм. Новая геометрия треугольника, 1902 год.