Какими свойствами не обладает выборочная дисперсия
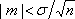
19. Выборочная
средняя, её свойства.
Вы́борочное
(эмпири́ческое) сре́днее —
это приближение теоретического среднего
распределения, основанное на выборке
из него.
Определение:
Пусть ![]() —выборкаизраспределения
—выборкаизраспределения
вероятности, определённая на
некоторомвероятностном
пространстве![]() .
.
Тогда её выборочным средним
называетсяслучайная
величина.![]()
Свойства
выборочного среднего :
Пусть ![]() —выборочная
—выборочная
функция распределенияданной
выборки. Тогда для любого
фиксированного![]() функция
функция![]() является
является
(неслучайной)функциейдискретного
распределения. Тогдаматематическое
ожиданиеэтого распределения
равно![]()
Выборочное
среднее — несмещённая
оценкатеоретического среднего:
![]() .
.
Выборочное
среднее — сильно
состоятельная оценкатеоретического
среднего:
![]() почти
почти
наверноепри![]() .
.
Выборочное
среднее — асимптотически
нормальная оценка. Пустьдисперсияслучайных
величин![]() конечна
конечна
и ненулевая, то есть![]() .
.
Тогда
![]() по
по
распределениюпри![]() ,
,
где ![]() —нормальное
—нормальное
распределениесо средним![]() и
и
дисперсией![]() .
.
Выборочное
среднее из нормальной выборки — эффективная
оценкаеё среднего
Выборочная
дисперсия в математической
статистике —
это оценка теоретической дисперсии
распределения на основе выборки.
Различают выборочную дисперсию и
несмещённую, или исправленную, выборочные
дисперсии.
Определения
Пусть ![]() —выборкаизраспределения
—выборкаизраспределения
вероятности. Тогда
Выборочная
дисперсия — это случайная
величина
![]() ,
,
где
символ ![]() обозначаетвыборочное
обозначаетвыборочное
среднее.
Несмещённая
(исправленная) дисперсия — это случайная
величина
![]() .
.
Замечание
Очевидно,
![]() .
.
Свойства
выборочных дисперсий
Выборочная
дисперсия является
теоретической дисперсиейвыборочного
распределения. Более точно,
пусть![]() —выборочная
—выборочная
функция распределенияданной
выборки. Тогда для любого
фиксированного![]() функция
функция![]() является
является
(неслучайной)функциейдискретного
распределения. Дисперсия этого
распределения равна![]() .
.
Обе
выборочные дисперсии являются состоятельными
оценкамитеоретической дисперсии.
Если![]() ,
,
то
![]() И
И![]() ,
,
где ![]() обозначаетсходимость
обозначаетсходимость
по вероятности.
Выборочная
дисперсия является смещённой
оценкойтеоретической дисперсии,
а исправленная выборочная дисперсия
несмещённой:
![]() ,
,
И
![]() .
.
Выборочная
дисперсия нормального
распределенияимеетраспределение
хи-квадрат. Пусть![]() .
.
Тогда
![]()
21. Статистические оценки: несмещенные, эффективные, состоятельные
Состоятельной
называют такую точечную статистическую
оценку, которая при n стрем к бесконечн
стремится по вероятности к оцениваемому
параметру. В частности, если дисперсия
несмещенной оценки при n стр к беск
стремится к нулю, то такая оценка
оказывается и состоятельной.
Рассмотрим
оценку θn числового
параметра θ, определенную при n =
1, 2, … Оценка θnназывается состоятельной,
если она сходится по вероятности к
значению оцениваемого параметра θ при
безграничном возрастании объема выборки.
Выразим сказанное более подробно.
Статистика θn является
состоятельной оценкой параметра θ тогда
и только тогда, когда для любого
положительного числа ε справедливо
предельное соотношение
![]()
Пример
3. Из
закона больших чисел следует, что
θn = ![]() является
является
состоятельной оценкой θ = М(Х) (в
приведенной выше теореме Чебышёва
предполагалось существование
дисперсии D(X); однако,
как доказал А.Я. Хинчин [6], достаточно
выполнения более слабого условия –
существования математического
ожидания М(Х)).
Пример
4. Все
указанные выше оценки параметров
нормального распределения являются
состоятельными.
Вообще,
все (за редчайшими исключениями) оценки
параметров, используемые в
вероятностно-статистических методах
принятия решений, являются состоятельными.
Пример
5.
Так, согласно теореме В.И. Гливенко,
эмпирическая функция распределенияFn(x) является
состоятельной оценкой функции
распределения результатов наблюденийF(x)
Несмещенной
называют такую точечную статистическую
оценку Q*математическое
ожидание которой равно оцениваемому
параметру: M(Q*)=Q
Второе
важное свойство оценок – несмещенность.
Несмещенная оценка θn –
это оценка параметра θ, математическое
ожидание которой равно значению
оцениваемого параметра: М(θn)
= θ.
Пример
6. Из
приведенных выше результатов следует,
что ![]() и
и ![]() являются
являются
несмещенными оценками
параметров m и σ2 нормального
распределения. Поскольку М(![]() )
)
= М(m**)
= m,
то выборочная медиана ![]() и
и
полусумма крайних членов вариационного
ряда m** —
также несмещенные оценки математического
ожидания mнормального
распределения. Однако
![]()
поэтому
оценки s2 и
(σ2)**
не являются состоятельными оценками
дисперсии σ2нормального
распределения.
Оценки,
для которых соотношение М(θn)
= θ неверно, называются смещенными. При
этом разность между математическим
ожиданием оценки θn и
оцениваемым параметром θ, т.е. М(θn)
– θ, называется смещением оценки.
Пример
7. Для
оценки s2,
как следует из сказанного выше, смещение
равно
М(s2)
— σ2 =
— σ2/n.
Смещение
оценки s2 стремится
к 0 при n →
∞.
Оценка,
для которой смещение стремится к 0, когда
объем выборки стремится к бесконечности,
называется асимптотически
несмещенной.
В примере 7 показано, что оценка s2 является
асимптотически несмещенной.
Практически
все оценки параметров, используемые в
вероятностно-статистических методах
принятия решений, являются либо
несмещенными, либо асимптотически
несмещенными. Для несмещенных оценок
показателем точности оценки служит
дисперсия – чем дисперсия меньше, тем
оценка лучше. Для смещенных оценок
показателем точности служит математическое
ожидание квадрата оценки М(θn –
θ)2.
Как следует из основных свойств
математического ожидания и дисперсии,
![]()
(3)
т.е.
математическое ожидание квадрата ошибки
складывается из дисперсии оценки и
квадрата ее смещения.
Для
подавляющего большинства оценок
параметров, используемых в
вероятностно-статистических методах
принятия решений, дисперсия имеет
порядок 1/n,
а смещение – не более чем 1/n,
где n –
объем выборки. Для таких оценок при
больших n второе
слагаемое в правой части (3) пренебрежимо
мало по сравнению с первым, и для них
справедливо приближенное равенство
![]()
(4)
где с –
число, определяемое методом вычисления
оценок θn и
истинным значением оцениваемого
параметра θ.
Эффективной
называют такую точечную статистическую
оценку, которая при фиксированном n
имеет наименьшую дисперсию.
С
дисперсией оценки связано третье важное
свойство метода оценивания –эффективность.
Эффективная оценка – это несмещенная
оценка, имеющая наименьшую дисперсию
из всех возможных несмещенных оценок
данного параметра.
Доказано
[11], что ![]() и
и ![]() являются
являются
эффективными оценками
параметров m и σ2нормального
распределения. В то же время для выборочной
медианы ![]() справедливо
справедливо
предельное соотношение
![]()
Другими
словами, эффективность выборочной
медианы, т.е. отношение дисперсии
эффективной оценки ![]() параметра m к
параметра m к
дисперсии несмещенной оценки ![]() этого
этого
параметра при больших n близка к 0,637.
Именно из-за сравнительно низкой
эффективности выборочной медианы в
качестве оценки математического ожидания
нормального распределения обычно
используют выборочное среднее
арифметическое.
Понятие
эффективности вводится для несмещенных
оценок, для которых М(θn)
= θ для всех возможных значений параметра
θ. Если не требовать несмещенности, то
можно указать оценки, при некоторых θ
имеющие меньшую дисперсию и средний
квадрат ошибки, чем эффективные.
Пример
8. Рассмотрим
«оценку» математического ожидания m1 ≡
0. Тогда D(m1) =
0, т.е. всегда меньше дисперсии D(![]() )
)
эффективной оценки ![]() .
.
Математическое ожидание среднего
квадрата ошибки dn(m1)
= m2,
т.е. при ![]() имеем dn(m1)
имеем dn(m1)
< dn(![]() ).
).
Ясно, однако, что статистику m1 ≡
0 бессмысленно рассматривать в качестве
оценки математического ожидания m.
Пример
9. Более
интересный пример рассмотрен американским
математиком Дж. Ходжесом:
![]()
Ясно,
что Tn –
состоятельная, асимптотически несмещенная
оценка математического ожидания m,
при этом, как нетрудно вычислить,
![]()
Последняя
формула показывает, что при m ≠
0 оценка Tn не
хуже ![]() (при
(при
сравнении по среднему квадрату ошибки dn),
а при m =
0 – в четыре раза лучше.
Подавляющее
большинство оценок θn,
используемых в вероятностно-статистических
методах, являются асимптотически
нормальными, т.е. для них справедливы
предельные соотношения:
![]()
для
любого х,
где Ф(х) –
функция стандартного нормального
распределения с математическим ожиданием
0 и дисперсией 1. Это означает, что для
больших объемов выборок (практически
— несколько десятков или сотен наблюдений)
распределения оценок полностью
описываются их математическими ожиданиями
и дисперсиями, а качество оценок –
значениями средних квадратов ошибок dn(θn).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Пусть наблюдаемая случайная величина имеет математическое ожидание и дисперсию .
I. Свойства выборочного среднего , как точечной оценки неизвестного математического ожидания.
1. Выборочное среднее является несмещенной оценкой неизвестного математического ожидания .
.
2. Выборочное среднее является состоятельной оценкой неизвестного математического ожидания .
Рассмотрим два способа доказательства этого свойства.
а) Последовательность независимых одинаково распределенных случайных величин , имеющих конечные математическое ожидание и дисперсиюподчиняется закону больших чисел, в соответствии с которым
.
б) Поскольку выборочное среднее является несмещенной оценкой неизвестного математического ожидания , то для доказательства состоятельности достаточно показать, что . А это следует из свойства аддитивности дисперсии для независимых случайных величин имеем:
.
3. Если закон распределения наблюдаемой случайной величины является нормальным с параметрами (то есть с неизвестным математическим ожиданием и известной дисперсией ), то выборочное среднее является эффективной оценкой параметра .
Покажем, что выборочное среднее обращает неравенство Рао-Крамера в равенство.
Для этого вычислим информацию Фишера о параметре , содержащуюся в одном наблюдении над случайной величиной :
.
Плотность вероятностей наблюдаемой случайной величины имеет вид:
,
а ее логарифм . Дифференцируя по , получаем:
.
Подставляя вместо аргумента случайную величину , для информации Фишера получаем выражение:
.
Следовательно,
.
Свойство 3 остается справедливым и в общей нормальной модели , когда неизвестны и математическое ожидание, и дисперсия.
II. Свойства выборочной дисперсии , как точечной оценки неизвестной дисперсии.
1. Выборочная дисперсия не является несмещенной оценкой неизвестной дисперсии . Она является асимптотически несмещенной оценкой .
Найдем математическое ожидание :
(поскольку при в силу независимости случайных величин )
.
Таким образом, выборочная дисперсия не является несмещенной оценкой дисперсии . Ее смещение . Поскольку , то выборочная дисперсия является асимптотически несмещенной оценкой дисперсии .
Несмещенную оценку дисперсии можно получить, умножив на коэффициент , компенсирующий ее смещение.
Несмещенная оценка дисперсии
называется исправленной выборочной дисперсией.
На практике исправленную выборочную дисперсию , как точечную оценку неизвестной дисперсии , используют чаще, чем просто выборочную дисперсию . Однако при больших оценки и отличаются крайне незначительно.
2. Выборочная дисперсия и исправленная выборочная дисперсия являются состоятельными оценками неизвестной дисперсии .
Как отмечалось ранее
.
В силу закона больших чисел , а . Поэтому
.
Поскольку при больших , то состоятельной оценкой дисперсии является и исправленная выборочная дисперсия .
3. Если закон распределения наблюдаемой случайной величины является нормальным с неизвестными параметрами , то исправленная выборочная дисперсия является асимптотически эффективной оценкой неизвестной дисперсии , то есть
,
где — эффективная оценка неизвестной дисперсии (без доказательства).
Поскольку при больших , то асимптотически эффективной оценкой дисперсии является и выборочная дисперсия .
Приветствую посетителей блога statanaliz.info. В данной статье рассмотрим, что такое «выборочная несмещенная дисперсия».
Тема не нова, так как с таким показателями как размах значений, среднее линейное отклонение, дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации мы уже знакомы.
Понятие о сплошном и выборочном наблюдении
С точки зрения охвата объекта исследования, статистический анализ можно разделить на два вида: сплошной и выборочный. Сплошной статанализ предполагает изучение генеральной совокупности данных, то есть всего явления во всем его многообразии без распространения выводов на другие элементы, не входящие в анализируемую совокупность. Из названия данного типа явствует, что наблюдению подвергаются тотально все элементы. Результат анализа распространяется на всю генеральную совокупность без каких-либо допущений и поправок на ошибку. Данный тип статистического исследования является наиболее полным и точным, так как дополнительные знания почерпнуть уже неоткуда – информация собрана со всех элементов объекта исследования. Это бесспорный плюс.
Отличным примером сплошного наблюдения является перепись населения. «Всесоюзная перепись населения» — красиво звучало! Кстати, советская статистика, как и наука в целом, была одной из самых лучших в мире. Денег на проведение сплошных обследований не жалели, так как при СССР статистика выполняла свою прямую функцию – исследовала реальность, без чего невозможно было строить «светлое будущее». При этом советские ученые-статистики справедливо критиковали буржуазную статистику за то, что те скрывают от народа реальное положение дел и используют статистику для промывки мозгов. Об этом, кстати, писали и сами буржуи. Более практичный пример сплошного наблюдения – опрос жителей многоэтажного дома на предмет заваривания мусоропровода. Опрашиваются все, результат дает вполне однозначный ответ об отношении жителей к мусоропроводу. Ошибки в выводах маловероятны.
Как бы там ни было, у сплошного наблюдения есть отрицательное качество: на организацию и проведение исследования могут потребоваться значительные ресурсы. Одно дело взять пробу из партии товаров, другое – проверять всю партию. Одно дело опросить тысячу прохожих на улице, совсем другое – организовать перепись населения.
В противовес сплошному придумали выборочное наблюдение. Название метода точно отражает его суть: из генеральной совокупности отбирается и анализируется только часть данных, а выводы распространяют на всю генеральную совокупность. Отбор данных происходит таким образом, чтобы выборка была репрезентативной, то есть, сохранила внутреннюю структуру и закономерности генеральной совокупности. Если это условие не соблюдено, то дальнейший анализ во многом теряет смысл.
Сам анализ выборочных данных происходит так же, как и при сплошном наблюдении (рассчитываются различные показатели, делаются прогнозы и т.д.), только с поправкой на ошибку. Это значит, что рассчитывая тот или иной показатель, мы понимаем, что при повторной выборке его значение будет другим. К примеру, провели опрос общественного мнения. Опрос показал, что за кандидата N желают проголосовать 60% опрошенных. Если провести еще один такой же опрос, даже в том же месте, то результат будет отличаться. То есть, взяв первое значение 60%, следует понимать, что с той или иной вероятностью оно могло быть, скажем, и 58%, и 62%. Точность и разброс выборочных показателей зависят от характера данных и их количества.
У выборочного наблюдения есть один существенный плюс и один минус, однако по сравнению со сплошным наблюдением крайности меняются местами. Плюс заключается в том, что для проведения выборочного обследования требуется гораздо меньше ресурсов. Минус – в том, что выборочное наблюдение всегда ошибочно. Поэтому основная задача проведения выборочного наблюдения – добиться максимальной точности при приемлемых затратах на его проведение.
Выборочная несмещенная дисперсия
И вот, стало быть, дисперсия. Дисперсия, как и доля или средняя арифметическая, также меняет свое значение от выборки к выборке, но здесь есть интересная особенность. Дисперсия ведь рассчитывается от средней величины, а она в свою очередь, тоже рассчитывается по выборке, то есть является ошибочной. Как же это обстоятельство влияет на саму дисперсию?
Если бы мы знали истинную среднюю величину (по генеральной совокупности), то ошибка дисперсии была бы связана только с нерепрезентативностью, то есть с тем, что данные в выборке оказались бы ближе или дальше от средней, чем в целом по генеральной совокупности. При этом при многократном повторении данные стремились бы к своему реальному расположению относительно средней.
Выборочный показатель, который при многократном повторении выборки стремится к своему теоретическому значению, называется несмещенной оценкой. Почему оценкой? Потому что мы не знаем реальное значение показателя (по генеральной совокупности), и с помощью выборочного наблюдения пытаемся его оценить. Оценка показателя – это есть его характеристика, рассчитанная по выборке.
Теперь смотрим внимательно на выборочную среднюю. Выборочная средняя – это несмещенная оценка математического ожидания, так как средняя из выборочных средних стремится к своему теоретическому значению по генеральной совокупности. Где она расположена? Правильно, в центре выборки! Средняя всегда находится в центре значений, по которым рассчитана – на то она и средняя. А раз выборочная средняя находится в центре выборки, то из этого следует, что сумма квадратов расстояний от каждого значения выборки до выборочной средней всегда меньше, чем до любой другой точки, в том числе и до генеральной средней. Это ключевой момент. А раз так, то дисперсия в каждой выборке будет занижена. Средняя из заниженных дисперсий также даст заниженное значение. То есть при многократном повторении эксперимента выборочная дисперсия не будет стремиться к своему истинному значению (как выборочная средняя), а будет смещена относительно истинного значения по генеральной совокупности.
Отклонение выборочной средней от генеральной показано на рисунке.
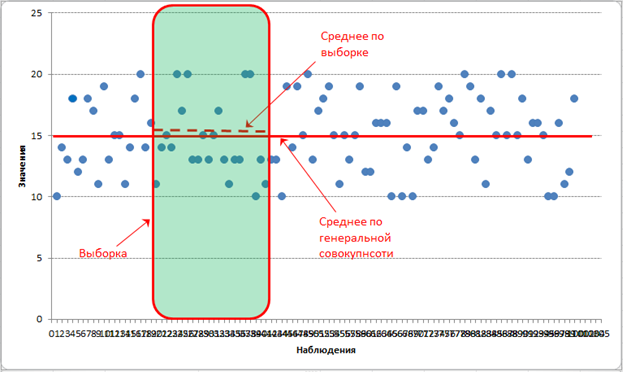
Несмещенность оценки – одна из важных характеристик статистического показателя. Смещенная оценка показателя заранее говорит о тенденции к ошибке. Поэтому показатели стараются оценивать таким образом, чтобы их оценки были несмещенными (как у средней арифметической). Чтобы решить проблему смещенности выборочной дисперсии, в ее расчет вносят корректировку – умножают на n/(n-1), либо сразу при расчете в знаменатель ставят не n, а n-1. Получается так.
Выборочная смещенная дисперсия:
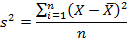
Выборочная несмещенная дисперсия:
![]()
Примечание. Для расчета выборочной и генеральной дисперсии в Excel есть специальная функция.
Под выборочной дисперсией понимают, как правило, именно несмещенный вариант.
Теперь посмотрим на практическую сторону отличия смещенной и несмещенной дисперсии. Соотношение между выборочной и генеральной дисперсией составляет n/n-1. Несложно догадаться, что с ростом n (объема выборки) данное выражение стремится к 1, то есть разница между значениями выборочной и генеральной дисперсиями уменьшается.
Так, в выборке из 11 наблюдений относительная разница составляет 11/10 = 10%. При 21 наблюдениях, отличие сокращается до 5%, при 31 наблюдении – до 3,3%, при 51 – до 2%, при 101 – до 1%. Короче, при достаточно большой выборке данных (50 и выше наблюдений) относительная разница между смещенной и несмещенной дисперсией практически исчезает. Оценка параметра, когда с ростом выборки его отклонение от теоретического значения уменьшается, называется асимптотически несмещенной оценкой.
При переходе к среднеквадратичном отклонению по выборке (корень из выборочной дисперсии) разница становится еще меньше.
Таким образом, эффект смещенной дисперсии проявляется в небольших выборках. В больших выборках можно использовать генеральную дисперсию, что как бы не усложняет и не упрощает жизнь. Вручную сейчас никто не считает. Все легко посчитать в Excel. Но понимать различие в терминологии и в сути показателей все же следует.
Из данной статьи неплохо бы усвоить следующее.
1. Формула генеральной дисперсии в выборке дает смещенную оценку.
2. В знаменателе несмещенной оценки n-1 вместо n.
3. При большом объеме выборки (от 100 наблюдений) разница между смещенной и несмещенной дисперсиями практически исчезает.
4. Стандартное отклонение по выборке – это корень из выборочной дисперсии.
До новых встреч на блоге statanaliz.info.
Поделиться в социальных сетях:
