Какими свойствами не обладает вектор
В данной теме мы подытожим раздел векторы, опишем все действия, которые
можно совершать над векторами и какими свойствами они обладают.
Действия над векторами
Определение
Вектором называется направленный отрезок $overline{A B}$ ,
где точка $A$ — начало, точка
$B$ — конец вектора.
Суммой $overline{a}+overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называют такой третий вектор
$overline{c}$, начало которого совпадает с началом
$overline{a}$, а конец — с концом
$overline{b}$ при условии, что конец вектора
$overline{a}$ и начало вектора
$overline{b}$ совпадают.
Свойства операции сложения:
1° $overline{a}+overline{b}=overline{b}+overline{a}$ — коммутативность
2° $(overline{a}+overline{b})+overline{c}=overline{a}+(overline{b}+overline{c})$ — ассоциативность
3° $overline{a}+overline{0}=overline{a}$
4° $overline{a}+(-overline{a})=overline{0}$
Определение
Разностью $overline{a}-overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называется вектор $overline{c}$
такой, что выполняется условие: $overline{b}+overline{c}=overline{a}$.
Произведением $alpha overline{a}$ вектора
$overline{a}$ на число
$alpha$ называется вектор
$overline{b}$, удовлетворяющий условиям:
- $overline{b} | overline{a}$
- $|overline{b}|=|alpha||overline{a}|$
- $overline{a} uparrow uparrow overline{b}$, если
$alpha>0$,
$overline{a} uparrow downarrow overline{b}$, если
$alpha
Свойства умножения вектора на число:
1° $(alpha pm beta) overline{a}=alpha overline{a} pm beta overline{a}$
2° $alpha(overline{a} pm overline{b})=alpha overline{a} pm alpha overline{b}$
3° $alpha(beta overline{a})=(alpha beta) overline{a}=beta(alpha overline{a})$
4° $1 cdot overline{a}=overline{a}$
5° $-1 cdot overline{a}=-overline{a}$
6° $0 cdot overline{a}=overline{0}$
Определение
Скалярным произведением двух ненулевых векторов $overline{a}$ и
$overline{b}$ называется число, равное произведению
длин этих векторов на косинус угла между ними:
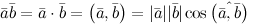
Свойства скалярного произведения:
1° $(overline{a}, overline{b})=(overline{b}, overline{a})$ — симметричность.
2° $(overline{a}, overline{a})=|overline{a}|^{2}$. Обозначается
$(overline{a}, overline{a})=overline{a}^{2}$ и называется скалярный квадрат.
3° Если $overline{a} neq overline{0}$, то 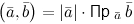
4° Если $overline{a} neq overline{0}$ и $overline{b} neq overline{0}$ и
$(overline{a}, overline{b})=0$, то $overline{a} perp overline{b}$. Верно и обратное утверждение.
5° $(overline{a}+overline{b}, overline{c})=(overline{a}, overline{c})+(overline{b}, overline{c})$
6° $(lambda overline{a}, overline{b})=lambda(overline{a}, overline{b})$
7° $(alpha overline{a}+beta overline{b}, gamma overline{c}+delta overline{d})=alpha gamma(overline{a}, overline{c})+alpha delta(overline{a}, overline{d})+beta gamma(overline{b}, overline{c})+beta delta(overline{b}, overline{d})$
Определение
Векторным произведением ненулевых векторов $overline{a}$ и
$overline{b}$ называется вектор $overline{c}$,
обозначаемый символом $[overline{a}, overline{b}]$ или
$overline{a} times overline{b}$, длина которого
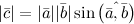 .
.
Свойства векторного произведения:
1° $[overline{a}, overline{b}]=overline{0}$, тогда и только тогда, когда
$overline{a} | overline{b}$
2° $[overline{a}, overline{b}]=-[overline{b}, overline{a}]$
3° Модуль векторного произведения $|[overline{a}, overline{b}]|$
равен площади параллелограмма, построенного на заданных векторах $overline{a}$ и
$overline{b}$ (рис. 2), т.е.
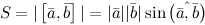
4° $[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]$
5° $left[overline{a}_{1}+overline{a}_{2}, overline{b}right]=left[overline{a}_{1}, overline{b}right]+left[overline{a}_{2}, overline{b}right] ;left[overline{a}, overline{b}_{1}+overline{b}_{2}right]=left[overline{a}, overline{b}_{1}right]+left[overline{a}, overline{b}_{2}right]$
Определение
Смешанным произведением трех векторов $overline{a}$,
$overline{b}$, $overline{c}$
называется число, равное скалярному произведению вектора $overline{a} times overline{b}$
на вектор $overline{c}$: $(overline{a}, overline{b}, overline{c})=([overline{a}, overline{b}], overline{c})$
Свойства смешанного произведения:
1° $(overline{a}, overline{b}, overline{c})=(overline{a},[overline{b}, overline{c}])$
2° $(overline{a}, overline{b}, overline{c})=(overline{b}, overline{c}, overline{a})=(overline{c}, overline{a}, overline{b})=-(overline{b}, overline{a}, overline{c})=-(overline{c}, overline{b}, overline{a})=-(overline{a}, overline{c}, overline{b})$
3° Три вектора компланарны тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})=0$
4° Тройка векторов является правой тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})>0$.
Если же $(overline{a}, overline{b}, overline{c})
5° $(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})$
6° $left(overline{a}_{1}+overline{a}_{2}, overline{b}, overline{c}right)=left(overline{a}_{1}, overline{b}, overline{c}right)+left(overline{a}_{2}, overline{b}, overline{c}right)$
7° $left(overline{a}, overline{b}_{1}+overline{b}_{2}, overline{c}right)=left(overline{a}, overline{b}_{1}, overline{c}right)+left(overline{a}, overline{b}_{2}, overline{c}right)$
8° $left(overline{a}, overline{b}, overline{c}_{1}+overline{c}_{2}right)=left(overline{a}, overline{b}, overline{c}_{1}right)+left(overline{a}, overline{b}, overline{c}_{2}right)$
9° $([overline{a}, overline{b}], overline{c})=overline{b}(overline{a}, overline{c})-overline{a}(overline{b}, overline{c}) ;(overline{a},[overline{b}, overline{c}])=overline{b}(overline{a}, overline{c})-overline{c}(overline{a}, overline{b})$
10° Тождество Якоби: $(overline{a},[overline{b}, overline{c}])+(overline{b},[overline{c}, overline{a}])+(overline{c},[overline{a}, overline{b}])=0$
Читать дальше: примеры решения задач с векторами.
Вы поняли, как решать? Нет?
Предварительные сведения
Перед тем как вводить свойства векторов, введем, непосредственно, понятие вектора, а также понятия их сложения, умножения на число и их равенства.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline{AB}$ — (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Чтобы ввести определение равенства двух векторов, сначала нужно разобраться с такими понятиями, как коллинеарность, сонаправленность, противоположная направленность двух векторов, а также длину вектора.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Осталось ввести понятие сложения векторов, а также их умножения на число.
Определение 8
Суммой векторов $overline{a+b}$ будем называть вектор $overline{c}=overline{AC}$, который построен следующим образом: От произвольной точки A отложем $overline{AB}=overline{a}$, далее от точки $B$ отложем $overline{BC}=overline{b}$ и соединим точку $A$ c точкой $C$ (рис. 6).
Определение 9
Произведением вектора $overline{a}$ на $k∈R$ будем называть вектор $overline{b}$ который будет удовлетворять условиям:
- $|overline{b}|=|k||overline{a}|$;
- $overline{a}↑↑overline{b}$ при $k≥0$ и, $overline{a}↑↓overline{b}$ при $k
Свойства сложения векторов
Введем свойства сложения для трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$:
Коммутативность сложения векторов:
$overline{α}+overline{β}=overline{β}+overline{α}$
Ассоциативность трех векторов по сложению:
$(overline{α}+overline{β})+overline{γ}=overline{α}+(overline{β}+overline{γ})$
Сложение с нулевым вектором:
$overline{α}+overline{0}=overline{α}$
Сложение противоположных векторов
$overline{α}+(overline{-α})=overline{0}$
Все эти свойства можно легко проверить с помощью построений таких векторов с помощью определения 8. В двух первых сравнением построенных векторов с правой и левой частей равенства, а в третьем и четвертом с помощью построения вектора с левой стороны.
Свойства умножения вектора на число
Введем свойства умножения для двух векторов $overline{α}$, $overline{β}$ и чисел $a$ и $b$.
- $a(overline{α}+overline{β})=aoverline{α}+aoverline{β}$
- $overline{α}(a+b)=overline{α}a+overline{α}b$
- $(ab)overline{α}=a(boverline{α})=b(aoverline{α})$
- $1cdot overline{α}=overline{α}$
Все эти свойства можно легко проверить с использованием определений 8 и 9. В двух первых сравнением построенных векторов с правой и левой частей равенства, в третьем сравнением всех векторов, входящих в равенство, и в четвертом с помощью построения вектора с левой стороны.
Пример задачи
Пример 1
Провести сложение векторов
$2overline{AB}+(2overline{BC}+3overline{AC})$
Решение.
Используя свойство сложения 2, получим:
$2overline{AB}+(2overline{BC}+3overline{AC})=(2overline{AB}+2overline{BC})+3overline{AC}$
Используя свойство умножения на число 1, получим:
$(2overline{AB}+2overline{BC})+3overline{AC}=2(overline{AB}+overline{BC})+3overline{AC}=2overline{BC}+3overline{AC}=5overline{AC}$
Ответ: $5overline{AC}$.
ОПРЕДЕЛЕНИЕ
Вектор представляет собой направленный сегмент, который обозначается (
A B
) (начиная с точки (
A
), заканчивается в точке (
B
)) или (
overline{a}
)
Если концы вектора задаются по их координатам в пространстве (
A=left(a_{1}, a_{2}, a_{3}right)
), (
B=left(b_{1}, b_{2}, b_{3}right)
) , то координаты вектора
(
A B=left(b_{1}-a_{1}, b_{2}-a_{2}, b_{3}-a_{3}right)
)
ОПРЕДЕЛЕНИЕ
Модуль (длина) вектора (
overline{c}=left(c_{1}, c_{2}, c_{3}right)
) представляет собой число, равное расстоянию от начала до конца вектора, оно вычисляется по формуле:
(
overline{c}=sqrt{c_{1}^{2}+c_{2}^{2}+c_{3}^{2}}
)
Вектор называется одиночным, если его длина равна единице. Вектор называется нулевым, если его длина равна нулю.
Векторы (
overline{a}
) и
(
overline{b}
) называются коллинеарными, если они либо лежат на одной прямой, либо на параллельных прямых.
ОПРЕДЕЛЕНИЕ
Суммой векторов (
overline{a}
) и (
overline{b}
) (конец вектора (
overline{a}
) совпадает с началом (
overline{b}
) называется вектор (
overline{c}
) , начало которого совпадает с началом вектора (
overline{a}
), конец – с концом вектора (
b
).Графически это выглядит так, как показано на рисунке (правило треугольника)
Операция сложения векторов обладает такими свойствами
1.(
overline{a}+overline{b}=overline{b}+overline{a}
)
(
(overline{a}+overline{b})+overline{c}=a+(overline{b}+overline{c})
)
ОПРЕДЕЛЕНИЕ
Разностью векторов (
overline{a}
) и (
b
) называется такой вектор (
overline{c}
) , который в сумме с вектором (
overline{b}
) дает вектор (
overline{a}
).
Если векторы (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) и (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) заданы своими координатами, то сумма/разность этих векторов
(
overline{a} pm overline{b}=left(a_{1} pm b_{1}, a_{2} pm b_{2}, a_{3} pm b_{3}right)
)
ОПРЕДЕЛЕНИЕ
Произведением вектора (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) на число (
alpha
) называется вектор (
alpha cdot overline{a}=left(alpha a_{1}, alpha a_{2}, alpha a_{3}right)
) , который параллелен вектору (
overline{a}
) , сонаправлен (
overline{a}
) , если (
alpha>0
) , и противоположно направлен, если (
alphaОПРЕДЕЛЕНИЕ
Скалярным произведением векторов (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) и (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) называется число (
(overline{a}, overline{b})
), равное сумме произведений соответствующих координат:
(
(overline{a}, overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}
)
Также скалярное произведение векторов можно вычислить как произведение модулей векторов на косинус угла между ними:
(
(overline{a}, overline{b})=|overline{a}||overline{b}| cos (overline{a}, overline{b})
)
Свойства скалярного произведения
1.(
(overline{a}, overline{b})=(overline{b}, overline{a})
)
2.(
(overline{a}, overline{b}+overline{c})=(overline{a}, overline{b})+(overline{a}, overline{c})
)
3.(
(lambda overline{a}, overline{b})=(overline{a}, lambda overline{b})=lambda(overline{a}, overline{b})
)
4.(
(overline{a}, overline{a}) geq 0
)
5.(
(overline{a}, overline{a})=|overline{a}|^{2}
)
6.(
(overline{a}, overline{b})=0 Leftrightarrow overline{a} perp overline{b}
)
Векторным произведением векторов (
a
) и (
overline{b}
) называется вектор (
overline{c}=overline{a} times overline{b}
) (или (
overline{c}=[overline{a}, b]
) )такой, что:
1) вектор (
overline{c}
) ортогонален векторам (
overline{a}
) и (
overline{b}
) :
(
overline{c} perp overline{a}, overline{c} perp overline{b}
)
2) векторы (
overline{a}
), (
overline{b}
) и (
overline{c}
) образуют правую тройку;
3) модуль векторного произведения равен площади параллелограмма построенного на векторах (
overline{a}
) и (
overline{b}
) :
(
|overline{c}|=|overline{a}| cdot|overline{b}| cdot sin (overline{a}, overline{b})
)
Если векторы (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
) и (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) заданы своими координатами, то векторное произведение находится по формуле:
(
[overline{a}, overline{b}]=left|begin{array}{ccc}{overline{i}} & {overline{j}} & {k} \ {a_{1}} & {a_{2}} & {a_{3}} \ {b_{1}} & {b_{2}} & {b_{3}}end{array}right|
)
Свойства векторного произведения
1.(
[overline{a}, overline{b}]=-[overline{b}, overline{a}]
)
2.(
[overline{a}, overline{b}+overline{c}]=[overline{a}, overline{b}]+[overline{a}, overline{c}]
)
3.(
[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]
)
4.(
[overline{a}, overline{b}]=overline{0}
) если векторы (
a
) и (
overline{b}
)коллинеарные
ОПРЕДЕЛЕНИЕ
Смешанным произведением (
overline{a}
), (
overline{b}
) и (
overline{c}
) векторов называется скалярное произведение вектора (
overline{a}
) на векторное произведение векторов (
overline{b}
) и (
overline{c}
) :
(
(overline{a}, overline{b}, overline{c})=(overline{a}, overline{b} times overline{c})
)
Свойства смешанного произведения
1. Смешанное произведение равно нулю, если векторы (
overline{a}
), (
overline{b}
) и (
overline{c}
) – компланарны
2. Модуль смешанного произведения трех некомпланарных векторов (
overline{a}
), (
overline{b}
) и (
vec{C}
) равен объему параллелепипеда, построенного на этих векторах
3. Смешанное произведение векторов (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
), (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
), (
overline{a}=left(a_{1}, a_{2}, a_{3}right)
), (
overline{b}=left(b_{1}, b_{2}, b_{3}right)
) и (
overline{c}=left(c_{1}, c_{2}, c_{3}right)
) , заданных своими координатами, равно значению определителя, составленного из координат этих векторов:
(
(overline{a}, overline{b}, overline{c})=left|begin{array}{lll}{a_{1}} & {a_{2}} & {a_{3}} \ {b_{1}} & {b_{2}} & {b_{3}} \ {c_{1}} & {c_{2}} & {c_{3}}end{array}right|
)
4. Если тройка векторов (
overline{a}
), (
overline{b}
) и (
overline{c}
) правая, то смешанное произведение (
(overline{a}, b, overline{c})>0
) , если левая, то (
(overline{a}, overline{b}, overline{c})5.(
(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})
)
6.(
(overline{a}+d, overline{b}, overline{c})=(overline{a}, overline{b}, overline{c})+(d, overline{b}, overline{c})
)
(
(overline{a}, overline{b}, overline{c})+(overline{b}, overline{c}, overline{a},)+(overline{c}, overline{a}, overline{b})=0
)
Примеры решения задач
ПРИМЕР 1
Для векторов (
overline{a}=(3,6,-2)
) и (
overline{b}=(2,-1,5)
) найти вектор (
5 overline{a}-3 overline{b}
)
Найдем векторы
(
5 overline{a}=5 cdot(3,6,-2)=(15,30,-10)
); (
3 overline{b}=3 cdot(2,-1,5)=(6,-3,15)
)
Найдем разность:
(
5 overline{a}-3 b=(15,30,-10)-(6,-3,15)=(15-6,30-(-3),-10-15)=(9,33,-25)
)
(
5 overline{a}-3 overline{b}=(9,33,-25)
)
ПРИМЕР 2
Найти скалярное и векторное произведение векторов (
overline{a}=(1,-3,5)
) и (
overline{b}=(1,2,0)
)
Скалярное произведение векторов равно сумме произведений соответствующих координат:
(
(overline{a}, overline{b})=a_{1} b_{1}+a_{2} b_{2}+a_{3} b_{3}=1 cdot 1+(-3) cdot 2+5 cdot 0=-5
)
Векторное произведение векторов, заданных своими координатами равно
(
[overline{a}, overline{b}]=left|begin{array}{ccc}{overline{i}} & {overline{j}} & {overline{k}} \ {a_{1}} & {a_{2}} & {a_{3}} \ {b_{1}} & {b_{2}} & {b_{3}}end{array}right|=left|begin{array}{ccc}{overline{i}} & {overline{j}} & {overline{k}} \ {1} & {-3} & {5} \ {1} & {2} & {0}end{array}right|=-10 overline{i}+5 overline{j}+5 overline{k}
)
т.е. (
[overline{a}, overline{b}]=(-10,5,5)
)
(
(overline{a}, overline{b})=-5,[overline{a}, overline{b}]=(-10,5,5)
)
Главная >> Лекции >> Аналитическая геометрия >> Основные свойства векторов
Определение Упорядоченную совокупность ( x1, x2, … , x n ) n вещественных чисел называют n-мерным вектором, а числа xi ( i = 1,…,n) — компонентами, или координатами, вектора.
Пример. Если, например, некоторый автомобильный завод должен выпустить в смену 50 легковых автомобилей, 100 грузовых, 10 автобусов, 50 комплектов запчастей для легковых автомобилей и 150 комплектов для грузовых автомобилей и автобусов, то производственную программу этого завода можно записать в виде вектора (50, 100, 10, 50, 150), имеющего пять компонент.
Обозначения. Векторы обозначают жирными строчными буквами или буквами с чертой или стрелкой наверху, например, a или . Два вектора называются равными, если они имеют одинаковое число компонент и их соответствующие компоненты равны.
Компоненты вектора нельзя менять местами, например, (3, 2, 5, 0, 1) и (2, 3, 5, 0, 1) разные вектора.
Операции над векторами. Произведением вектора x = (x1, x2 , … ,xn) на действительное число λ называется вектор λ x = (λ x1, λ x2, … , λ xn).
Суммой векторов x = (x1, x2, … ,xn) и y = (y1, y2 , … ,yn) называется вектор x + y = (x1 + y1, x2 + y2, … , x n+ + yn).
Пространство векторов. N—мерное векторное пространство Rn определяется как множество всех n-мерных векторов, для которых определены операции умножения на действительные числа и сложение.
Экономическая иллюстрация. Экономическая иллюстрация n-мерного векторного пространства: пространство благ (товаров). Под товаром мы будем понимать некоторое благо или услугу, поступившие в продажу в определенное время в определенном месте. Предположим, что существует конечное число наличных товаров n; количества каждого из них, приобретенные потребителем, характеризуются набором товаров
x = (x1, x2, …, xn),
где через xi обозначается количество i-го блага, приобретенного потребителем. Будем считать, что все товары обладают свойством произвольной делимости, так что может быть куплено любое неотрицательное количество каждого из них. Тогда все возможные наборы товаров являются векторами пространства товаров C = { x = (x1, x2, … , xn) xi ≥ 0, i =1,…,n}.
Линейная независимость. Система e1, e2, … , em n-мерных векторов называется линейно зависимой, если найдутся такие числа λ1, λ2, … , λm, из которых хотя бы одно отлично от нуля, что выполняется равенство λ1e1 + λmem = 0; в противном случае данная система векторов называется линейно независимой, то есть указанное равенство возможно лишь в случае, когда все λ1=λ2=…=λm=0. Геометрический смысл линейной зависимости векторов в R3, интерпретируемых как направленные отрезки, поясняют следующие теоремы.
Теорема 1. Система, состоящая из одного вектора, линейно зависима тогда и только тогда, когда этот вектор нулевой.
Теорема 2. Для того, чтобы два вектора были линейно зависимы, необходимо и достаточно, чтобы они были коллинеарны (параллельны).
Теорема 3. Для того, чтобы три вектора были линейно зависимы, необходимо и достаточно, чтобы они были компланарны (лежали в одной плоскости).
Левая и правая тройки векторов. Тройка некомпланарных векторов a, b, c называется правой, если наблюдателю из их общего начала обход концов векторов a, b, c в указанном порядке кажется совершающимся по часовой стрелке. B противном случае a, b, c — левая тройка. Все правые (или левые) тройки векторов называются одинаково ориентированными.
Базис и координаты. Тройка e1, e2, e3 некомпланарных векторов в R3 называется базисом, а сами векторы e1, e2,e3 — базисными. Любой вектор a может быть единственным образом разложен по базисным векторам, то есть представлен в виде
а = x1 e1 + x2e2 + x3 e3, (1.1)
числа x1, x2, x3 в разложении (1.1) называются координатами вектора a в базисе e1, e2,e3 и обозначаются a(x1, x2, x3).
Ортонормированный базис. Если векторы e1, e2,e3 попарно перпендикулярны и длина каждого из них равна единице, то базис называется ортонормированным, а координаты x1, x2, x3 — прямоугольными. Базисные векторы ортонормированного базиса будем обозначать i, j, k.
Будем предполагать, что в пространстве R3 выбрана правая система декартовых прямоугольных координат {0, i, j, k}.
Векторное произведение. Векторным произведением вектора а на вектор b называется вектор c, который определяется следующими тремя условиями:
1. Длина вектора c численно равна площади параллелограмма, построенного на векторах a и b, т. е.
c = |a||b| sin (a^b).
2. Вектор c перпендикулярен к каждому из векторов a и b.
3. Векторы a, b и c, взятые в указанном порядке, образуют правую тройку.
Для векторного произведения c вводится обозначение c = [ab] или
c = a × b.
Если векторы a и b коллинеарны, то sin(a^b) = 0 и [ab] = 0, в частности, [aa] = 0. Векторные произведения ортов: [ij]= k, [jk] = i, [ki]= j.
Если векторы a и b заданы в базисе i, j, k координатами a(a1, a2, a3), b(b1, b2, b3), то
Смешанное произведение. Если векторное произведение двух векторов а и b скалярноумножается на третий вектор c, то такое произведение трех векторов называется смешанным произведением и обозначается символом a b c.
Если векторы a, b и c в базисе i, j, k заданы своими координатами
a(a1, a2, a3), b(b1, b2, b3), c(c1, c2, c3), то
.
Смешанное произведение имеет простое геометрическое толкование — это скаляр, по абсолютной величине равный объему параллелепипеда, построенного на трех данных векторах.
Если векторы образуют правую тройку, то их смешанное произведение есть число положительное, равное указанному объему; если же тройка a, b, c — левая, то a b c<0 и V = — a b c, следовательно V = |a b c| .
Координаты векторов, встречающиеся в задачах первой главы, предполагаются заданными относительно правого ортонормированного базиса. Единичный вектор, сонаправленный вектору а, обозначается символом ао. Символом r=ОМ обозначается радиус-вектор точки М, символами а, АВ или |а| , |АВ| обозначаются модули векторов а и АВ.
Пример 1.2. Найдите угол между векторами a = 2m+4n и b = m-n, где m и n — единичные векторы и угол между m и n равен 120о.
Решение. Имеем: cos φ = ab/ab, ab = (2m+4n) (m-n) = 2 m2 — 4n2 +2mn =
= 2 — 4+2cos120o = — 2 + 2(-0.5) = -3; a = ; a2 = (2m+4n) (2m+4n) =
= 4 m2 +16mn+16 n2 = 4+16(-0.5)+16=12, значит a = . b = ; b2 =
= (m-n)(m-n) = m2 -2mn+ n2= 1-2(-0.5)+1 = 3, значит b = . Окончательно имеем: cos φ == -1/2, φ = 120o.
Пример 1.3. Зная векторы AB(-3,-2,6) и BC(-2,4,4),вычислите длину высоты AD треугольника ABC.
Решение. Обозначая площадь треугольника ABC через S, получим:
S = 1/2 BC AD. Тогда AD=2S/BC, BC= = = 6,
S = 1/2| AB × AC|. AC=AB+BC, значит, вектор AC имеет координаты
.
= -16(2 + ). |AB×AC| = = 16; S = 8,откуда
AD = =.
Пример 1.4. Даны два вектора a(11,10,2) и b(4,0,3). Найдите единичный вектор c, ортогональный векторам a и b и направленный так, чтобы упорядоченная тройка векторов a, b, c была правой.
Решение. Обозначим координаты вектора c относительно данного правого ортонормированного базиса через x, y, z.
Поскольку c ⊥ a, c ⊥ b, то ca = 0, cb = 0. По условию задачи требуется, чтобы c = 1 и a b c >0.
Имеем систему уравнений для нахождения x,y,z: 11x +10y + 2z = 0, 4x+3z=0, x2 +y2 + z2 = 0.
Из первого и второго уравнений системы получим z = -4/3 x, y = -5/6 x. Подставляя y и z в третье уравнение, будем иметь: x2 = 36/125, откуда
x = ± . Используя условие a b c >0, получим неравенство
С учетом выражений для z и y перепишем полученное неравенство в виде: 625/6 x > 0, откуда следует, что x>0. Итак, x = , y = -, z =-.
