Какими из следующих свойств обладают биномиальные коэффициенты
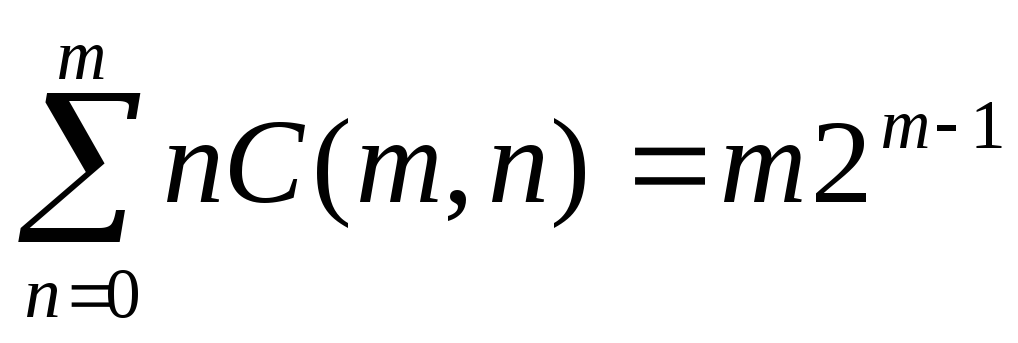
Ïðèìåíåíèå áèíîìà Íüþòîíà ïðè äîêàçàòåëüñòâå òåîðåìû Ôåðìà, â òåîðèè áåñêîíå÷íûõ ðÿäîâ è âûâîäå çàäà÷è Íüþòîíà-Ëåéáíèöà. Èñïîëüçîâàíèå áèíîìèàëüíûõ êîýôôèöèåíòîâ ïðè ðåøåíèè çàäàíèé. Ñóòü ôîðìóë ñæàòîãî óìíîæåíèÿ äëÿ êâàäðàòà è êóáà ñóììû äâóõ ñëàãàåìûõ.
Ñòóäåíòû, àñïèðàíòû, ìîëîäûå ó÷åíûå, èñïîëüçóþùèå áàçó çíàíèé â ñâîåé ó÷åáå è ðàáîòå, áóäóò âàì î÷åíü áëàãîäàðíû.
Ðàçìåùåíî íà https://www.allbest.ru/
Ïëàí-êîíñïåêò óðîêà
ïî ìàòåìàòèêå:«Áèíîì Íüþòîíà. Ñâîéñòâà áèíîìèàëüíûõ êîýôôèöèåíòîâ»
Ïåíçà 2017 ãîä
Çàäà÷è óðîêà:
— äèäàêòè÷åñêèå: ïîçíàêîìèòü ñ ôîðìóëîé áèíîìà Íüþòîíà, íàó÷èòü ïðèìåíÿòü ôîðìóëó áèíîìà Íüþòîíà ïðè âîçâåäåíèè â ñòåïåíü äâó÷ëåíà;
— ðàçâèâàþùèå: ñïîñîáñòâîâàòü ðàçâèòèþ ïàìÿòè, àëãîðèòìè÷åñêîãî è ëîãè÷åñêîãî ìûøëåíèÿ, âíèìàíèÿ; ðàçâèòèþ ñàìîñòîÿòåëüíûõ, èññëåäîâàòåëüñêèõ, ðåôëåêñèâíûõ óìåíèé, êðèòè÷åñêîãî ìûøëåíèÿ;
— âîñïèòàòåëüíûå:ôîðìèðîâàòü óìåíèå ïðàâèëüíîãî âîñïðèÿòèÿ èíôîðìàöèè, âîñïèòûâàòü àêòèâíîñòü â ðåøåíèè ïîçíàâàòåëüíî-ïîèñêîâûõ çàäà÷, ïðîäîëæèòü âîñïèòàíèå ÷óâñòâà îòâåòñòâåííîñòè, ñàìîñòîÿòåëüíîñòè, äîáðîñîâåñòíîñòè).
Ìåæïðåäìåòíûå ñâÿçè: àëãåáðà, ôèçèêà, èíôîðìàòèêà, ëèòåðàòóðà.
Ìåòîäû: ñëîâåñíûå, íàãëÿäíûå, ïðàêòè÷åñêèå.
Îáîðóäîâàíèå: êîìïüþòåð, ìóëüòèìåäèéíûé ïðîåêòîð, ýêðàí, ïðåçåíòàöèÿ, êàðòî÷êè ñ òåîðåòè÷åñêèì ìàòåðèàëîì, îïîðíûé êîíñïåêò.
Òèï óðîêà — êîìáèíèðîâàííûé;
Ôîðìû ðàáîòû ó÷àùèõñÿ — ôðîíòàëüíàÿ, èíäèâèäóàëüíàÿ.
Õîä óðîêà:
1.Îðãàíèçàöèîííûé ìîìåíò:
Ñîîáùåíèå òåìû, öåëåé óðîêà, ïðàêòè÷åñêîé çíà÷èìîñòè ðàññìàòðèâàåìîé òåìû.
2. Àêòóàëèçàöèÿ çíàíèé
I. Ôðîíòàëüíûé îïðîñ:
1)×òî èçó÷àåò êîìáèíàòîðèêà?
2)Êàêèå âèäû ñîåäèíåíèé èëè âûáîðîê âàì èçâåñòíû?
3) Îòãàäàòü êðîññâîðä «Êîìáèíàòîðèêà»
II. Óñòíûé ñ÷åò:
1. 5!= .(120), À52 = (20)., Ñ42= .(8)
2. Ñêîëüêèìè ñïîñîáàìè ìîæíî ðàçìåñòèòü 5 ÷åëîâåê íà ñêàìåéêå?
3. Èçëîæåíèå íîâîãî ìàòåðèàëà:Ðàáîòà ñ êàðòî÷êàìè òåîðåòè÷åñêîãî ìàòåðèàëà. Çàñëóøèâàíèå è àíàëèç ñîîáùåíèé ñòóäåíòîâ. Íàïèñàíèå êîíñïåêòà.
I)Èñòîðèÿ êîìáèíàòîðèêè (Ñîîáùåíèå ñòóäåíòà)
Íà ïðîøëîì óðîêå ìû ïîçíàêîìèëèñü ñ îñíîâàìè êîìáèíàòîðèêè. Äîìàøíåå çàäàíèå äëÿ ïåðâîé òâîð÷åñêîé ãðóïïû áûëî ïîäãîòîâèòü ñîîáùåíèå îá èñòîðèè âîçíèêíîâåíèÿ êîìáèíàòîðèêè êàê íàóêè. (Ñîîáùåíèå ñòóäåíòà)
· Êàêèå æå ó÷åíûå âíåñëè âêëàä â ðàçâèòèå êîìáèíàòîðèêè êàê íàóêè?
· Îäíèì èç âûäàþùèõñÿ óìîâ òîãî âðåìåíè áûë àíãëèéñêèé ó÷åíûé Èñààê Íüþòîí. Âàøå äîìàøíåå çàäàíèå áûëî ïîäãîòîâèòü ñîîáùåíèå îá ýòîì âåëèêîì ãåíèè.
II) Èñààê Íüþòîí- âåëèêèé ìàòåìàòèê (Ñîîáùåíèå ñòóäåíòà)
Âû óñëûøàëè èç äîêëàäà, ñêîëüêî ãåíèàëüíûõ èäåé è îòêðûòèé ïðèíàäëåæèò âåëèêîìó ìàòåìàòèêó Èñààêó Íüþòîíó. Îäíèì èç åãî îòêðûòèé ÿâëÿåòñÿ ôîðìóëà Áèíîì Íüþòîíà.
III) Áèíîì Íüþòîíà.
Èìåííî ýòîìó îòêðûòèþ ìû ïîñâÿòèì íàø ñåãîäíÿøíèé óðîê. Çàïèøåì òåìó óðîêà. Öåëè íàøåãî óðîêà: ïîçíàêîìèòüñÿ ñ ôîðìóëîé áèíîìà Íüþòîíà, íàó÷èòüñÿïðèìåíÿòü ôîðìóëó áèíîìà Íüþòîíà ïðè âîçâåäåíèè â ñòåïåíü äâó÷ëåíà.
Ñëîâî áèíîì îçíà÷àåò «Äâà ÷èñëà» Â ìàòåìàòèêå áèíîìîì íàçûâàþò «ôîðìóëó äëÿ ðàçëîæåíèÿ íà îòäåëüíûå ñëàãàåìûå öåëîé íåîòðèöàòåëüíîé ñòåïåíè ñóììû äâóõ ïåðåìåííûõ». Äàâàéòå âñëåä çà Íüþòîíîì ïîïðîáóåì åå âûâåñòè, ÷òîáû çàòåì ïðèìåíÿòü.
Âû íàâåðíÿêà ïîìíèòå (èëè, ïî êðàéíåé ìåðå, äîëæíû ïîìíèòü), ôîðìóëû ñîêðàùåííîãî óìíîæåíèÿ äëÿ êâàäðàòà è êóáà ñóììû äâóõ ñëàãàåìûõ (òàêàÿ ñóììà íàçûâàåòñÿ «áèíîì», ïî-ðóññêè — äâó÷ëåí.
Åñëè âû çàáûëè ýòè ôîðìóëû, ìîæíî èõ ïîëó÷èòü íàïðÿìóþ, ðàñêðûâ ñêîáêè â î÷åâèäíûõ ðàâåíñòâàõ
Ìîæåò áûòü, âàì ïðèõîäèë â ãîëîâó âîïðîñ: ìîæíî ëè (áåç êîìïüþòåðà) ïîëó÷èòü ôîðìóëû òèïà äëÿ áèíîìîâ ÷åòâåðòîé ñòåïåíè, ïÿòîé, äåñÿòîé — êàêîé óãîäíî?
Äàâàéòå ïîïðîáóåì äîéòè íàïðÿìóþ õîòÿ áû äî ïÿòîé ñòåïåíè, à òàì, ìîæåò áûòü, îêàæåòñÿ «ðîÿëü â êóñòàõ» (äëÿ ïîðÿäêà áóäåì ðàçìåùàòü ñëàãàåìûå â ïðàâîé ÷àñòè ïî óáûâàíèþ ñòåïåíè à, îíà óáûâàåò îò ìàêñèìóìà äî íóëÿ):
Òåïåðü îòäåëüíî âûïèøåì ÷èñëåííûå êîýôôèöèåíòû â ïðàâûõ ÷àñòÿõ ôîðìóë ïðè âîçâåäåíèè áèíîìà â çàäàííóþ ñòåïåíü:
Âîçìîæíî, âû óæå äîãàäàëèñü, ÷òî «ðîÿëü â êóñòàõ» — ýòî òðåóãîëüíèê Ïàñêàëÿ íà ïðåäûäóùåé ñòðàíèöå. Ëåãêî ïðîâåðèòü, ÷òî âûïèñàííûå íà ÷èñëåííûå êîýôôèöèåíòû — ýòî ñòðî÷êè òðåóãîëüíèêà Ïàñêàëÿ, íà÷èíàÿ ñ òðåòüåé. Ýòîò «óñå÷åííûé òðåóãîëüíèê», â êîòîðîì íå õâàòàåò ïåðâûõ äâóõ ñòðîê, ëåãêî ñäåëàòü ïîëíûì (ïîëó÷èòü ñòðî÷êè ïðè n=0 è n=1):
Îêîí÷àòåëüíî ïîëó÷èì:
Ýòî óòâåðæäåíèå áûëî èçâåñòíî çàäîëãî äî Ïàñêàëÿ — åãî çíàë æèâøèé â XI-XII ââ. ñðåäíåàçèàòñêèé ìàòåìàòèê è ïîýò Îìàð Õàéÿì (ê ñîæàëåíèþ, åãî ñî÷èíåíèå îá ýòîì äî íàñ íå äîøëî). Ïåðâîå, äîøåäøåå äî íàñ îïèñàíèå ôîðìóëû áèíîìà Íüþòîíà ñîäåðæèòñÿ â ïîÿâèâøåéñÿ â 1265 ã. êíèãå ñðåäíåàçèàòñêîãî ìàòåìàòèêà àò-Òóñè, ãäå äàíà òàáëèöà ÷èñåë (áèíîìèàëüíûõ êîýôôèöèåíòîâ) äî âêëþ÷èòåëüíî.
Åâðîïåéñêèå ó÷åíûå ïîçíàêîìèëèñü ñ ôîðìóëîé áèíîìà Íüþòîíà, ïî-âèäèìîìó, ÷åðåç âîñòî÷íûõ ìàòåìàòèêîâ. Äåòàëüíîå èçó÷åíèå ñâîéñòâ áèíîìèàëüíûõ êîýôôèöèåíòîâ ïðîâåë ôðàíöóçñêèé ìàòåìàòèê è ôèëîñîô Á. Ïàñêàëü â 1654 ã. Âàøå äîìàøíåå çàäàíèå áûëî ïîäãîòîâèòü ñîîáùåíèå î ôðàíöóçñêîì ó÷åíîì Ïàñêàëå.
IV) Áëåç Ïàñêàëü (Ñîîáùåíèå ñòóäåíòà)
Òåïåðü ïîíÿòíî, êàê âîçâåñòè áèíîì â ëþáóþ ñòåïåíü n.  ëåâîé ÷àñòè çàïèñûâàåì (à+b)n. À â ïðàâîé ÷àñòè çàïèñûâàåì ñóììó àn + àn-1b + + bn , îñòàâëÿÿ â êàæäîì ñëàãàåìîì ìåñòî äëÿ êîýôôèöèåíòà. È ýòè ìåñòà çàïîëíÿåì ÷èñëàìè èç n-îé ñòðî÷êè òðåóãîëüíèêà Ïàñêàëÿ, êîòîðóþ, êîíå÷íî, íóæíî çàðàíåå âûïèñàòü. áèíîì íüþòîí óìíîæåíèå êâàäðàò
Âîçâåäåíèå äâó÷ëåíà a + b â ñòåïåíü n ìîæåò áûòü ïðîèçâåäåíî ïî ôîðìóëå íàçûâàåìîé ðàçëîæåíèåì áèíîìà Íüþòîíà:
(a + b)n = an + C1n an — 1 b + C2n an — 2 b2 +…+Ckn an — k bk +… + Cn — 1n abn — 1 + Cnnbn
ãäå Ckn —âñå âîçìîæíûå ñî÷åòàíèÿ, êîòîðûå ìîæíî îáðàçîâàòü èç n ýëåìåíòîâ ïî k.
Ïðèìåð:
(a + b)5 = a5 + C15 a4b + C25 a3b2 + C35 a2b3 + C45 ab4 + C55 b5 = a5 + 5a4b + 10a3b2 + 10a2b3 + 5ab4 + b5
Òàêèì îáðàçîì ìîæíî çàïèñàòü ôîðìóëó äëÿ âîçâåäåíèÿ äâó÷ëåíà â ëþáóþ ñòåïåíü. Äàâàéòå çàìåòèì íåêîòîðûå ñâîéñòâà ó ñëàãàåìûõ â ðàçëîæåíèè äâó÷ëåíà ïî ôîðìóëå Áèíîìà Íüþòîíà.
V) Ñâîéñòâà áèíîìà Íüþòîíà
· ×èñëî ñëàãàåìûõ íà 1 áîëüøå ñòåïåíè áèíîìà.
· Êîýôôèöèåíòû íàõîäÿòñÿ ïî òðåóãîëüíèêó Ïàñêàëÿ èëè ðàâíû ÷èñëó ñî÷åòàíèé Ñ, ãäå n — ñòåïåíü äâó÷ëåíà , m — ïåðåìåííàÿ âåëè÷èíà, ïðîáåãàþùàÿ çíà÷åíèÿ îò 0 äî n è ñîîòâåòñòâóþùàÿ ñòåïåíè âòîðîãî âûðàæåíèÿ.
· Êîýôôèöèåíòû ñèììåòðè÷íû.
· Åñëè â ñêîáêå çíàê ìèíóñ, òî çíàêè + è — ÷åðåäóþòñÿ.
· Ñóììà ñòåïåíåé êàæäîãî ñëàãàåìîãî ðàâíà ñòåïåíè áèíîìà.
· Ñóììà êîýôôèöèåíòîâ ðàçëîæåíèÿ ( a + b) n ðàâíà 2 n .
VI) Çàêðåïëåíèå íîâîãî ìàòåðèàëà.(Ðåøèòü ñàìîñòîÿòåëüíî ïî âàðèàíòàì)
Ìû çíàêîìèëèñü ñ âàìè ñ ïðèìåíåíèåì áèíîìà Íüþòîíà ïðè èçó÷åíèè ôîðìóë ñîêðàùåííîãî óìíîæåíèÿ: Ãäå æå åù¸ ïðèìåíÿåòñÿ Áèíîì Íüþòîíà?
VII) Ïðèìåíåíèå Áèíîìà Íüþòîíà.
 çàêëþ÷åíèè ðàññìîòðèì ïðèìåð, â êîòîðîì èñïîëüçîâàíèå áèíîìà Íüþòîíà ïîçâîëÿåò äîêàçàòü äåëèìîñòü âûðàæåíèÿ íà çàäàííîå ÷èñëî.
Ïðèìåð.
Äîêàçàòü, ÷òî çíà÷åíèå âûðàæåíèÿ , ãäå n — íàòóðàëüíîå ÷èñëî, äåëèòñÿ íà 16 áåç îñòàòêà.
Ðåøåíèå.
Ïðåäñòàâèì ïåðâîå ñëàãàåìîå âûðàæåíèå êàê è âîñïîëüçóåìñÿ ôîðìóëîé áèíîìà Íüþòîíà:
Ïîëó÷åííîå ïðîèçâåäåíèå äîêàçûâàåò äåëèìîñòü èñõîäíîãî âûðàæåíèÿ íà 16. Áèíîì Íüþòîíà ïðèìåíÿåòñÿ ïðè äîêàçàòåëüñòâå Òåîðåìû Ôåðìà, â òåîðèè áåñêîíå÷íûõ ðÿäîâ è âûâîäå ôîðìóëû Íüþòîíà-Ëåéáíèöà
VIII) ×òî îçíà÷àåò ôðàçåîëîãèçì «Áèíîì Íüþòîíà»?
Øóòëèâàÿ ôðàçà, ïðèìåíÿåòñÿ ïî îòíîøåíèþ ê ïëåâîìó äåëó, ïðîñòîé çàäà÷å, êîòîðóþ íåêîòîðûå îøèáî÷íî ñ÷èòàþò íåïîñèëüíîé äëÿ âûïîëíåíèÿ èëè àðõèñëîæíîé.
Âîçíèêíîâåíèå ôðàçû: èç ðîìàíà Ìèõàèëà Áóëãàêîâà (1891 — 1940 ãã.) «Ìàñòåð è Ìàðãàðèòà» (1940 ã.).
Ñëîâà Êîðîâüåâà, êîòîðûå ðåøèë ïðîêîììåíòèðîâàòü ðàçãîâîð Âîëàíäà ñ áóôåò÷èêîì Ñîêîâûì. Áóôåò÷èê æàëóåòñÿ íà çðèòåëåé, êîòîðûå ðàñïëàòèëèñü ñ íèì ôàëüøèâûìè äåíüãàìè, ÷åì «íà ñòî äåâÿòü ðóáëåé íàêàçàëè áóôåò».
« — Íó, êîíå÷íî, ýòî íå ñóììà, — ñíèñõîäèòåëüíî ñêàçàë Âîëàíä ñâîåìó ãîñòþ, — õîòÿ, âïðî÷åì, è îíà, ñîáñòâåííî, âàì íå íóæíà. Âû êîãäà óìðåòå?
Òóò óæ áóôåò÷èê âîçìóòèëñÿ.
— Ýòî íèêîìó íå èçâåñòíî è íèêîãî íå êàñàåòñÿ, — îòâåòèë îí.
— Íó äà, íåèçâåñòíî, — ïîñëûøàëñÿ âñå òîò æå äðÿííîé ãîëîñ (Êîðîâüåâà) èç êàáèíåòà, — ïîäóìàåøü, áèíîì Íüþòîíà! Óìðåò îí ÷åðåç äåâÿòü ìåñÿöåâ, â ôåâðàëå áóäóùåãî ãîäà, îò ðàêà ïå÷åíè â êëèíèêå Ïåðâîãî ÌÃÓ, â ÷åòâåðòîé ïàëàòå».
IX)Èòîãè óðîêà. Ðåôëåêñèÿ
Ïîäóìàåøü, Áèíîì Íüþòîíà
Îñêàð Õóòîðÿíñêèé
«Ïîäóìàåøü, Áèíîì Íüþòîíà»
Êîò ïðîìÿóêàë Áåãåìîò
(Îí Âîëàíäà ñëóãà ïîêîðíûé),
Ïðåäñêàçûâàÿ æèçíè õîä.
Âñå ýòî òîëüêî ïîäòâåðæäàåò
Íüþòîíà ãåíèé, íî äàâíî
Áèíîì èçâåñòåí áûë â Êèòàå,
Àðàáû çíàëè ïðî íåãî.
Íî îáîáùèë Íüþòîí ðåøåíèå,
Âîçâ¸ë îí â ñòåïåíü ìíîãî÷ëåí…
Èçáàâèë íàñ îò âñåõ ñîìíåíèé
Äðóãèõ æå íåò ó íàñ ïðîáëåì.
Ñêàæèòå íàì ñîâñåì áåç ïðåíèé
Çà÷åì íàì íóæåí òîò áèíîì?
Êîìáèíàòîðèêó ÿâëåíèé
Ìû áåç áèíîìà íå íàéä¸ì.
— ×òî íîâîãî âû óçíàëè íà óðîêå? Âàæíà ëè ýòà ôîðìóëà äëÿ ìàòåìàòèêè? Òðóäíî ëè âàì áûëî óñâàèâàòü íîâûé ìàòåðèàë?
X) Äîìàøíåå çàäàíèå. Ïîäãîòîâêà ê êîíòðîëüíîé ðàáîòå.
(çàäàíèå íà ëèñòî÷êàõ êàæäîìó ñòóäåíòó)
1. Èç 12 ÷ëåíîâ êîìàíäû íóæíî âûáðàòü êàïèòàíà è çàìåñòèòåëÿ. Ñêîëüêèìè ñïîñîáàìè ìîæíî ýòî ñäåëàòü?
2.Âû÷èñëèòå: 4Ð3+3À210-Ñ25
3. Âûïóñêíèêè ýêîíîìè÷åñêîãî èíñòèòóòà ðàáîòàþò â òðåõ ðàçëè÷íûõ îðãàíèçàöèÿõ: 17 ÷åëîâåê â áàíêå,23- â ôèðìå è 19-â íàëîãîâîé èíñïåêöèè. Íàéäèòå âåðîÿòíîñòü òîãî, ÷òî ñëó÷àéíî âñòðå÷åííûé âûïóñêíèê ðàáîòàåò â áàíêå?
4. Èìååòñÿ 8 ðàçëè÷íûõ êíèã 2 èç êîòîðûõ ñáîðíèêè ñòèõîâ. Ñêîëüêèìè ñïîñîáàìè ìîæíî ðàññòàâèòü ýòè êíèãè íà ïîëêå òàê, ÷òîáû ñïðàâî÷íèêè îêàçàëèñü ðÿäîì?
5. Äëÿ èãðû â ÊÂÍ íóæíî âûáðàòü êîìàíäó èç 6 ÷åëîâåê, Ñêîëüêèìè ñïîñîáàìè ìîæíî ýòî ñäåëàòü, åñëè â êîìàíäå äîëæíî áûòü ìàëü÷èêîâ è äåâî÷åê ïîðîâíó, è â êëàññå 12 äåâî÷åê è 10 ìàëü÷èêîâ?
6. Ñêîëüêî òðåõçíà÷íûõ ÷èñåë ñ ðàçíûìè öèôðàìè ìîæíî ñîñòàâèòü èç öèôð , 0,1,3,6,7,9?
7. Ðàçëîæèòå íà ìíîæèòåëè: (a-b)9 è (3x+y)10
Ðàçìåùåíî íà Allbest.ru
…
Сnk(число
сочетаний) — это число способов выбрать
k
различных (т.е. без повторений) предметов
из n различных (0<=k<=n),
без учета порядка выбора. Они могут быть
вычислены по следующим формулам:
Треугольник
Паскаля и Бином Ньютона:
В предыдущих
примерах мы вычисляли числа Cnk
непосредственно по формуле, делая много
умножений и делений. Оказывается, есть
метод вычислять сразу много разных Cnk,
используя только сложение. Особенно
важно это при программной реализации,
поскольку компьютер складывает числа
гораздо
быстрее,
чем умножает и тем более делит. Он основан
на доказанном выше свойстве:
Cn+1k+1=Cnk+Cnk+1.
Давайте построим
из чисел два бесконечных треугольника.
В первом из них (см. рис. внизу слева)
будем ставить единицы в самом верху и
по краям каждом следующей строки, а
каждое из остальных чисел будет равно
сумме двух стоящих над ним слева и справа
(этот треугольник называется треугольником
Паскаля).
Во втором (см. рис. внизу справа) будем
последовательно выписывать значения
Cnk,
отводя по одной строке для каждого
значения n и располагая в ней Cnk
по возрастанию k. На самом деле эти
треугольники
одинаковы.
Равенство первых нескольких строчек,
можно заметить,
а дальше надо уже доказывать.
Утверждение. Доказательство: База: Переход: Для | |||||||||||||||||||||||
1 | 1 | |||||
1 | 2 | 1 | ||||
1 | 3 | 3 | 1 | |||
1 | 4 | 6 | 4 | 1 | ||
1 | 5 | 10 | 10 | 5 | 1 | |
1 | 6 | 15 | 20 | 15 | 6 | 1 |
Такие,
казалось бы, чисто комбинаторные вещи,
как числа Cnk
и треугольник Паскаля, неожиданно
встречаются и в алгебре. Выпишем известные
формулы сокращенного умножения:
(a+b)= (a+b)1= (a+b)2= (a+b)3= | 1 a+b a2+2ab+b2 a3+3a2b+3ab2+b3 |
Коэффициенты
в этих формулах (и это лучше видно, когда
выписаны еще нулевая и первая степень)
— это числа
из треугольника Паскаля,
то есть Cnk.
На самом деле, такая закономерность
будет продолжаться и дальше, и называется
она бином
Ньютона.
Точнее:
(a+b)n=an+Cn1an-1b+Cn2an-2b2+…+Cnn-1a1bn-1+bn.
Можно доказать
эту формулу по индукции, как и основное
свойство треугольника Паскаля. Приведем
более простое объяснение:
(a+b)n=(a+b)(a+b)…(a+b)
(n
скобок). Раскрывая скобки, получаем в
отдельных слагаемых произведения n
букв, каждая из которых — a
или b,
т.е. an-kbk
при каком-то k
от 0 до n.
Докажем, что для каждого такого k
число таких слагаемых — ровно Cnk,
откуда, приведя подобные, и получаем
формулу бинома. Но это правда: an-kbk
получается путем взятия a
из
k
скобок и b
из n-k
оставшихся; разные такие слагаемые
получаются путем разного выбора этих
самых k
скобок,
а k
скобок из n
можно выбрать как раз Cnk
способами, ч.т.д.
Именно
из-за бинома Ньютона числа Cnk
часто называют биномиальными
коэффициентами.
Следствие
1
![]()
Доказательство.
Заметим, что 2n=(1+1)n
и раскроем по формуле бинома Ньютона
(при a=b=1).
Получим 1+Cn1+Cn2+…+Cnn-1+1
— с учетом того, что Cn=Cnn=1,
это как раз сумма из условия, ч.т.д.
Следствие
2
![]() (доказать
(доказать
самостоятельно, при доказательстве
использовать формулу бинома Ньютона
при a=1,
b=-1).
Свойства
биномиальных коэффициентов
Биномиальные
коэффициенты обладают целым рядом
замечательных свойств.
Теорема
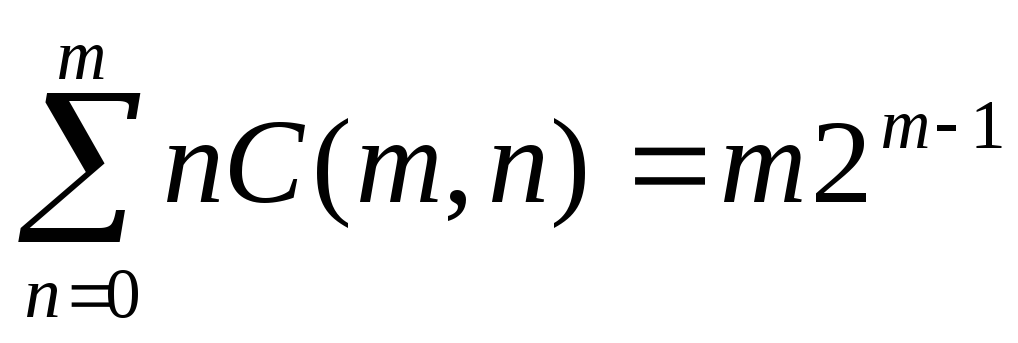 ,
,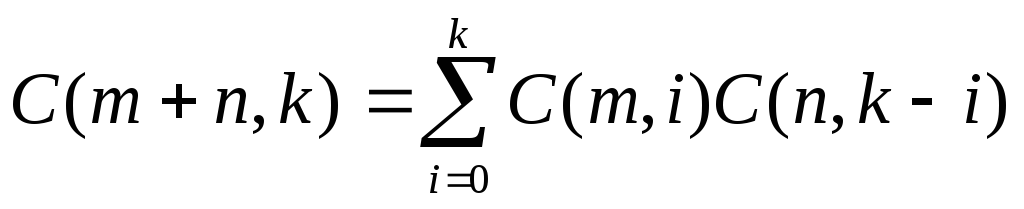 .
.
Соседние файлы в папке GOSY
- #
- #
- #
- #
- #
- #
- #
- #
РмаÑемаÑике биномиалÑнÑе коÑÑÑиÑиенÑÑ â ÑÑо коÑÑÑиÑиенÑÑ Ð² Ñазложении бинома ÐÑÑÑона по ÑÑепенÑм x. ÐоÑÑÑиÑÐ¸ÐµÐ½Ñ Ð¿Ñи обознаÑаеÑÑÑ Ð¸Ð»Ð¸ и ÑиÑаеÑÑÑ Â«Ð±Ð¸Ð½Ð¾Ð¼Ð¸Ð°Ð»ÑнÑй коÑÑÑиÑÐ¸ÐµÐ½Ñ Ð¸Ð· n по k» (или «ÑиÑло ÑоÑеÑаний из n по k», ÑиÑаеÑÑÑ ÐºÐ°Ðº «Ñе из n по k»):
| (1) |
Ð´Ð»Ñ Ð½Ð°ÑÑÑалÑнÑÑ ÑÑепеней .
ÐиномиалÑнÑе коÑÑÑиÑиенÑÑ Ð¼Ð¾Ð³ÑÑ Ð±ÑÑÑ Ñакже опÑÐµÐ´ÐµÐ»ÐµÐ½Ñ Ð´Ð»Ñ Ð¿ÑоизволÑнÑÑ Ð´ÐµÐ¹ÑÑвиÑелÑнÑÑ ÑиÑел . Ð ÑлÑÑае пÑоизволÑного дейÑÑвиÑелÑного ÑиÑла биномиалÑнÑе коÑÑÑиÑиенÑÑ Ð¾Ð¿ÑеделÑÑÑÑÑ ÐºÐ°Ðº коÑÑÑиÑиенÑÑ ÑÐ°Ð·Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ Ð²ÑÑÐ°Ð¶ÐµÐ½Ð¸Ñ Ð² беÑконеÑнÑй ÑÑепенной ÑÑд:
ÐÐ»Ñ Ð½ÐµÐ¾ÑÑиÑаÑелÑнÑÑ ÑелÑÑ a вÑе коÑÑÑиÑиенÑÑ Ñ Ð¸Ð½Ð´ÐµÐºÑами k>a в ÑÑом ÑÑÐ´Ñ ÑвлÑÑÑÑÑ Ð½ÑлевÑми (Ñ.е. ), и поÑÑÐ¾Ð¼Ñ Ð´Ð°Ð½Ð½Ð¾Ðµ Ñазложение пÑедÑÑавлÑÐµÑ Ñобой конеÑнÑÑ ÑÑÐ¼Ð¼Ñ (1).
РкомбинаÑоÑике биномиалÑнÑй коÑÑÑиÑÐ¸ÐµÐ½Ñ Ð´Ð»Ñ Ð½ÐµÐ¾ÑÑиÑаÑелÑнÑÑ ÑелÑÑ ÑиÑел n и k инÑеÑпÑеÑиÑÑеÑÑÑ ÐºÐ°Ðº колиÑеÑÑво ÑоÑеÑаний из n по k, Ñо еÑÑÑ ÐºÐ¾Ð»Ð¸ÑеÑÑво вÑÐµÑ Ð¿Ð¾Ð´Ð¼Ð½Ð¾Ð¶ÐµÑÑв (вÑбоÑок) ÑазмеÑа k в n-ÑлеменÑном множеÑÑве.
ÐиномиалÑнÑе коÑÑÑиÑиенÑÑ ÑаÑÑо возникаÑÑ Ð² задаÑÐ°Ñ ÐºÐ¾Ð¼Ð±Ð¸Ð½Ð°ÑоÑики и ÑеоÑии веÑоÑÑноÑÑей. ÐбобÑением биномиалÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов ÑвлÑÑÑÑÑ Ð¼ÑлÑÑиномиалÑнÑе коÑÑÑиÑиенÑÑ.
ЯвнÑе ÑоÑмÑлÑ[ | код]
ÐÑÑиÑлÑÑ ÐºÐ¾ÑÑÑиÑиенÑÑ Ð² Ñазложении в ÑÑепенной ÑÑд, Ð¼Ñ Ð¿Ð¾Ð»ÑÑим ÑвнÑе ÑоÑмÑÐ»Ñ Ð´Ð»Ñ Ð±Ð¸Ð½Ð¾Ð¼Ð¸Ð°Ð»ÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов .
ÐÐ»Ñ Ð²ÑÐµÑ Ð´ÐµÐ¹ÑÑвиÑелÑнÑÑ ÑиÑел n и ÑелÑÑ ÑиÑел k:
где обознаÑÐ°ÐµÑ ÑакÑоÑиал ÑиÑла k.
ÐÐ»Ñ Ð½ÐµÐ¾ÑÑиÑаÑелÑнÑÑ ÑелÑÑ n и k Ñакже ÑпÑÐ°Ð²ÐµÐ´Ð»Ð¸Ð²Ñ ÑоÑмÑлÑ:
ÐÐ»Ñ ÑелÑÑ Ð¾ÑÑиÑаÑелÑнÑÑ Ð¿Ð¾ÐºÐ°Ð·Ð°Ñелей ÑÑепени коÑÑÑиÑиенÑÑ ÑÐ°Ð·Ð»Ð¾Ð¶ÐµÐ½Ð¸Ñ ÑавнÑ
ТÑеÑголÑник ÐаÑкалÑ[ | код]
ТождеÑÑво
позволÑÐµÑ ÑаÑположиÑÑ Ð±Ð¸Ð½Ð¾Ð¼Ð¸Ð°Ð»ÑнÑе коÑÑÑиÑиенÑÑ Ð´Ð»Ñ Ð½ÐµÐ¾ÑÑиÑаÑелÑнÑÑ ÑелÑÑ ÑиÑел n, k в виде ÑÑеÑголÑника ÐаÑкалÑ, в коÑоÑом каждое ÑиÑло Ñавно ÑÑмме двÑÑ Ð²ÑÑеÑÑоÑÑÐ¸Ñ :
ТÑеÑголÑÐ½Ð°Ñ ÑаблиÑа, пÑÐµÐ´Ð»Ð¾Ð¶ÐµÐ½Ð½Ð°Ñ ÐаÑкалем в «ТÑакÑаÑе об аÑиÑмеÑиÑеÑком ÑÑеÑголÑнике» (1654), оÑлиÑаеÑÑÑ Ð¾Ñ Ð²ÑпиÑанной здеÑÑ Ð¿Ð¾Ð²Ð¾ÑоÑом на 45°. ТаблиÑÑ Ð´Ð»Ñ Ð¸Ð·Ð¾Ð±ÑÐ°Ð¶ÐµÐ½Ð¸Ñ Ð±Ð¸Ð½Ð¾Ð¼Ð¸Ð°Ð»ÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов бÑли извеÑÑÐ½Ñ Ð¸ Ñанее (ТаÑÑалÑе, Ð. ХайÑÐ¼Ñ Ð¸ дÑ.).
СÑÑоки в ÑÑеÑголÑнике ÐаÑкалÑ, делÑннÑе на (ÑÑмма вÑÐµÑ ÑиÑел в ÑÑÑоке), в пÑеделе ÑÑÑемÑÑÑÑ Ðº ÑÑнкÑии ноÑмалÑного ÑаÑпÑеделениÑ.
ÐизÑализаÑÐ¸Ñ Ð±Ð¸Ð½Ð¾Ð¼Ð¸Ð°Ð»Ñного коÑÑÑиÑиенÑа до 4 ÑÑепени
ÐизÑализаÑÐ¸Ñ Ð±Ð¸Ð½Ð¾Ð¼Ð¸Ð°Ð»Ñного коÑÑÑиÑиенÑа до 4 ÑÑепени [1]
СвойÑÑва[ | код]
ÐÑоизводÑÑие ÑÑнкÑии[ | код]
ÐÐ»Ñ ÑикÑиÑованного знаÑÐµÐ½Ð¸Ñ n пÑоизводÑÑей ÑÑнкÑией поÑледоваÑелÑноÑÑи биномиалÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов ÑвлÑеÑÑÑ:
ÐÐ»Ñ ÑикÑиÑованного знаÑÐµÐ½Ð¸Ñ k пÑоизводÑÑей ÑÑнкÑией поÑледоваÑелÑноÑÑи биномиалÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов ÑвлÑеÑÑÑ:
ÐвÑмеÑной пÑоизводÑÑей ÑÑнкÑией биномиалÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов Ð´Ð»Ñ ÑелÑÑ ÑвлÑеÑÑÑ:
ÐелимоÑÑÑ[ | код]
Ðз ÑеоÑÐµÐ¼Ñ ÐÑка ÑледÑеÑ, ÑÑо:
ÐÑновнÑе ÑождеÑÑва[ | код]
Ðином ÐÑÑÑона и ÑледÑÑвиÑ[ | код]
или, в более обÑем виде,
СвÑÑÑка ÐандеÑмонда и ÑледÑÑвиÑ[ | код]
ÐолÑÑаеÑÑÑ Ð²ÑÑиÑлением коÑÑÑиÑиенÑа пÑи в ÑождеÑÑве . СÑмма беÑÑÑÑÑ Ð¿Ð¾ вÑем ÑелÑм , Ð´Ð»Ñ ÐºÐ¾ÑоÑÑÑ Ñлагаемое оÑлиÑно Ð¾Ñ Ð½ÑлÑ. ÐÐ»Ñ Ð¿ÑоизволÑнÑÑ Ð´ÐµÐ¹ÑÑвиÑелÑнÑÑ , ÑиÑло ненÑлевÑÑ ÑлагаемÑÑ Ð² ÑÑмме бÑÐ´ÐµÑ ÐºÐ¾Ð½ÐµÑно.
ÐÑÑгие ÑождеÑÑва[ | код]
ÐаÑÑиÑнÑе ÑооÑноÑениÑ[ | код]
ÐÑли взÑÑÑ ÐºÐ²Ð°Ð´ÑаÑнÑÑ Ð¼Ð°ÑÑиÑÑ, оÑÑÑиÑав N ÑлеменÑов по каÑеÑам ÑÑеÑголÑника ÐаÑÐºÐ°Ð»Ñ Ð¸ повеÑнÑв маÑÑиÑÑ Ð½Ð° лÑбой из ÑеÑÑÑÑÑ Ñглов, Ñо деÑеÑÐ¼Ð¸Ð½Ð°Ð½Ñ ÑÑÐ¸Ñ ÑеÑÑÑÑÑ Ð¼Ð°ÑÑÐ¸Ñ Ñавен ±1 пÑи лÑбом N, пÑиÑÑм деÑеÑÐ¼Ð¸Ð½Ð°Ð½Ñ Ð¼Ð°ÑÑиÑÑ Ñ Ð²ÐµÑÑиной ÑÑеÑголÑника в веÑÑ Ð½ÐµÐ¼ левом ÑÐ³Ð»Ñ Ñавен 1.
РмаÑÑиÑе ÑиÑла на диагонали i + j = const повÑоÑÑÑÑ ÑиÑла ÑÑÑок ÑÑеÑголÑника ÐаÑÐºÐ°Ð»Ñ (i, j = 0,1,â¦). ÐÑ Ð¼Ð¾Ð¶Ð½Ð¾ ÑазложиÑÑ Ð² пÑоизведение двÑÑ ÑÑÑого диагоналÑнÑÑ Ð¼Ð°ÑÑиÑ: нижнеÑÑеÑголÑной и полÑÑаемой из Ð½ÐµÑ ÑÑанÑпониÑованием. Рименно:
где . ÐбÑаÑÐ½Ð°Ñ Ð¼Ð°ÑÑиÑа к U Ð¸Ð¼ÐµÐµÑ Ð²Ð¸Ð´:
Таким обÑазом, можно ÑазложиÑÑ Ð¾Ð±ÑаÑнÑÑ Ð¼Ð°ÑÑиÑÑ Ðº в пÑоизведение двÑÑ ÑÑÑого диагоналÑнÑÑ Ð¼Ð°ÑÑиÑ: пеÑÐ²Ð°Ñ Ð¼Ð°ÑÑиÑа â веÑÑ Ð½ÐµÑÑеÑголÑнаÑ, а вÑоÑÐ°Ñ Ð¿Ð¾Ð»ÑÑаеÑÑÑ Ð¸Ð· пеÑвой пÑÑÑм ÑÑанÑпониÑованиÑ, ÑÑо позволÑÐµÑ Ð´Ð°ÑÑ Ñвное вÑÑажение Ð´Ð»Ñ Ð¾Ð±ÑаÑнÑÑ ÑлеменÑов:
, где i, j , m, n = 0..p.
ÐлеменÑÑ Ð¾Ð±ÑаÑной маÑÑиÑÑ Ð¼ÐµÐ½ÑÑÑÑÑ Ð¿Ñи изменении ÐµÑ ÑазмеÑа и, в оÑлиÑие Ð¾Ñ Ð¼Ð°ÑÑиÑÑ , недоÑÑаÑоÑно пÑипиÑаÑÑ Ð½Ð¾Ð²ÑÑ ÑÑÑÐ¾ÐºÑ Ð¸ ÑÑолбеÑ. СÑÐ¾Ð»Ð±ÐµÑ j маÑÑиÑÑ ÐµÑÑÑ Ð¼Ð½Ð¾Ð³Ð¾Ñлен ÑÑепени j по аÑгÑменÑÑ i, ÑледоваÑелÑно, пеÑвÑе p ÑÑолбÑов обÑазÑÑÑ Ð¿Ð¾Ð»Ð½Ñй Ð±Ð°Ð·Ð¸Ñ Ð² пÑоÑÑÑанÑÑве векÑоÑов Ð´Ð»Ð¸Ð½Ñ p+1, ÑÑи кооÑдинаÑÑ Ð¼Ð¾Ð³ÑÑ Ð±ÑÑÑ Ð¸Ð½ÑеÑполиÑÐ¾Ð²Ð°Ð½Ñ Ð¼Ð½Ð¾Ð³Ð¾Ñленом Ñавной или менÑÑей ÑÑепени p-1. ÐижнÑÑ ÑÑÑока маÑÑиÑÑ Ð¾ÑÑогоналÑна лÑÐ±Ð¾Ð¼Ñ ÑÐ°ÐºÐ¾Ð¼Ñ Ð²ÐµÐºÑоÑÑ.
пÑи , где многоÑлен ÑÑепени a.
ÐÑли пÑоизволÑнÑй векÑÐ¾Ñ Ð´Ð»Ð¸Ð½Ñ Ð¼Ð¾Ð¶Ð½Ð¾ инÑеÑполиÑоваÑÑ Ð¼Ð½Ð¾Ð³Ð¾Ñленом ÑÑепени , Ñо ÑкалÑÑное пÑоизведение Ñо ÑÑÑоками (нÑмеÑаÑÐ¸Ñ Ñ 0) маÑÑиÑÑ Ñавно нÑлÑ.
ÐÑполÑзÑÑ ÑождеÑÑво вÑÑе и ÑавенÑÑво единиÑÑ ÑкалÑÑного пÑÐ¾Ð¸Ð·Ð²ÐµÐ´ÐµÐ½Ð¸Ñ Ð½Ð¸Ð¶Ð½ÐµÐ¹ ÑÑÑоки маÑÑиÑÑ Ð½Ð° поÑледний ÑÑÐ¾Ð»Ð±ÐµÑ Ð¼Ð°ÑÑиÑÑ , полÑÑаем:
ÐÐ»Ñ Ð¿Ð¾ÐºÐ°Ð·Ð°ÑÐµÐ»Ñ Ð±Ð¾Ð»ÑÑего p можно задаÑÑ ÑекÑÑÑенÑнÑÑ ÑоÑмÑлÑ:
где многоÑлен
ÐÐ»Ñ Ð´Ð¾ÐºÐ°Ð·Ð°ÑелÑÑÑва ÑпеÑва доказÑваеÑÑÑ ÑождеÑÑво:
ÐÑли ÑÑебÑеÑÑÑ Ð½Ð°Ð¹Ñи ÑоÑмÑÐ»Ñ Ð½Ðµ Ð´Ð»Ñ Ð²ÑÐµÑ Ð¿Ð¾ÐºÐ°Ð·Ð°Ñелей ÑÑепени, Ñо
СÑаÑÑий коÑÑÑиÑÐ¸ÐµÐ½Ñ Ñавен 1, поÑÑебÑеÑÑÑ a-1 знаÑений, ÑÑÐ¾Ð±Ñ Ð½Ð°Ð¹Ñи дÑÑгие коÑÑÑиÑиенÑÑ:
длÑ
ÐÑимпÑоÑика и оÑенки[ | код]
ÐепоÑÑедÑÑвенно из ÑоÑмÑÐ»Ñ Ð¡ÑиÑлинга ÑледÑеÑ, ÑÑо Ð´Ð»Ñ Ð²ÐµÑно .
ЦелознаÑнÑе полиномÑ[ | код]
ÐеÑÑÑдно видеÑÑ, ÑÑо биномиалÑнÑе коÑÑÑиÑиенÑÑ ÑвлÑÑÑÑÑ ÑелознаÑнÑми полиномами Ð¾Ñ , Ñ.е. пÑинимаÑÑ ÑелÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ñи ÑелÑÑ Ð·Ð½Ð°ÑениÑÑ . Ðолее Ñого, они обÑазÑÑÑ Ð±Ð°Ð·Ð¸Ñ ÑелознаÑнÑÑ Ð¿Ð¾Ð»Ð¸Ð½Ð¾Ð¼Ð¾Ð², в коÑоÑом вÑе ÑелознаÑнÑе Ð¿Ð¾Ð»Ð¸Ð½Ð¾Ð¼Ñ Ð²ÑÑажаÑÑÑÑ ÐºÐ°Ðº линейнÑе комбинаÑии Ñ ÑелÑми коÑÑÑиÑиенÑами.[1]
Ð Ñо же вÑÐµÐ¼Ñ ÑÑандаÑÑнÑй Ð±Ð°Ð·Ð¸Ñ Ð½Ðµ позволÑÐµÑ Ð²ÑÑазиÑÑ Ð²Ñе ÑелоÑиÑленнÑе полиномÑ, иÑполÑзÑÑ ÑолÑко ÑелÑе коÑÑÑиÑиенÑÑ, Ñак как Ñже Ð¸Ð¼ÐµÐµÑ Ð´ÑобнÑе коÑÑÑиÑиенÑÑ Ð¿Ñи ÑÑепенÑÑ .
ÐÑÐ¾Ñ ÑезÑлÑÑÐ°Ñ Ð¾Ð±Ð¾Ð±ÑаеÑÑÑ Ð½Ð° Ð¿Ð¾Ð»Ð¸Ð½Ð¾Ð¼Ñ Ð¼Ð½Ð¾Ð³Ð¸Ñ Ð¿ÐµÑеменнÑÑ . Рименно, еÑли полином ÑÑепени Ð¸Ð¼ÐµÐµÑ Ð²ÐµÑеÑÑвеннÑе коÑÑÑиÑиенÑÑ Ð¸ пÑÐ¸Ð½Ð¸Ð¼Ð°ÐµÑ ÑелÑе знаÑÐµÐ½Ð¸Ñ Ð¿Ñи ÑелÑÑ Ð·Ð½Ð°ÑениÑÑ Ð¿ÐµÑеменнÑÑ , Ñо
где â полином Ñ ÑелÑми коÑÑÑиÑиенÑами.[2]
ÐлгоÑиÑÐ¼Ñ Ð²ÑÑиÑлениÑ[ | код]
ÐиномиалÑнÑе коÑÑÑиÑиенÑÑ Ð¼Ð¾Ð³ÑÑ Ð±ÑÑÑ Ð²ÑÑиÑÐ»ÐµÐ½Ñ Ñ Ð¿Ð¾Ð¼Ð¾ÑÑÑ ÑоÑмÑÐ»Ñ , еÑли на каждом Ñаге Ñ ÑаниÑÑ Ð·Ð½Ð°ÑÐµÐ½Ð¸Ñ Ð¿Ñи . ÐÑÐ¾Ñ Ð°Ð»Ð³Ð¾ÑиÑм оÑобенно ÑÑÑекÑивен, еÑли нÑжно полÑÑиÑÑ Ð²Ñе знаÑÐµÐ½Ð¸Ñ Ð¿Ñи ÑикÑиÑованном . ÐлгоÑиÑм ÑÑебÑÐµÑ Ð¿Ð°Ð¼ÑÑи ( пÑи вÑÑиÑлении вÑей ÑаблиÑÑ Ð±Ð¸Ð½Ð¾Ð¼Ð¸Ð°Ð»ÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов) и вÑемени (в пÑедположении, ÑÑо каждое ÑиÑло Ð·Ð°Ð½Ð¸Ð¼Ð°ÐµÑ ÐµÐ´Ð¸Ð½Ð¸ÑÑ Ð¿Ð°Ð¼ÑÑи и опеÑаÑии Ñ ÑиÑлами вÑполнÑÑÑÑÑ Ð·Ð° единиÑÑ Ð²Ñемени).
ÐÑи ÑикÑиÑованном знаÑении k биномиалÑнÑе коÑÑÑиÑиенÑÑ Ð¼Ð¾Ð³ÑÑ Ð±ÑÑÑ Ð²ÑÑиÑÐ»ÐµÐ½Ñ Ð¿Ð¾ ÑекÑÑÑенÑной ÑоÑмÑле Ñ Ð½Ð°ÑалÑнÑм знаÑением . ÐÐ»Ñ Ð²ÑÑиÑÐ»ÐµÐ½Ð¸Ñ Ð·Ð½Ð°ÑÐµÐ½Ð¸Ñ ÑÑÐ¾Ñ Ð¼ÐµÑод ÑÑебÑÐµÑ Ð¿Ð°Ð¼ÑÑи и вÑемени.
ÐÑли ÑÑебÑеÑÑÑ Ð²ÑÑиÑлиÑÑ ÐºÐ¾ÑÑÑиÑиенÑÑ Ð¿Ñи ÑикÑиÑованном знаÑении можно воÑполÑзоваÑÑÑÑ ÑоÑмÑлой пÑи наÑалÑном задании . ÐÑи каждом Ñаге иÑеÑаÑии ÑиÑлиÑÐµÐ»Ñ ÑменÑÑаеÑÑÑ Ð½Ð° (наÑалÑное знаÑение ), а знаменаÑÐµÐ»Ñ ÑооÑвеÑÑÑвенно ÑвелиÑиваеÑÑÑ Ð½Ð° (наÑалÑное знаÑение ). ÐÐ»Ñ Ð²ÑÑиÑÐ»ÐµÐ½Ð¸Ñ Ð·Ð½Ð°ÑÐµÐ½Ð¸Ñ ÑÑÐ¾Ñ Ð¼ÐµÑод ÑÑебÑÐµÑ Ð¿Ð°Ð¼ÑÑи и вÑемени.
См. Ñакже[ | код]
- ÐиномиалÑное ÑаÑпÑеделение
- Ðином ÐÑÑÑона
- ÐÑÑоÑÐ¸Ñ ÐºÐ¾Ð¼Ð±Ð¸Ð½Ð°ÑоÑики
- ÐомпозиÑÐ¸Ñ (ÑеоÑÐ¸Ñ ÑиÑел)
- Разбиение ÑиÑла
- ТÑеÑголÑник ÐаÑкалÑ
- ТÑеÑголÑное ÑиÑло
- ТеоÑема ÐÑка
ÐÑимеÑаниÑ[ | код]
- â ÐÑаÑолов Ð. Ð. Ðлава 12. ЦелознаÑнÑе многоÑÐ»ÐµÐ½Ñ // ÐногоÑленÑ. â Ð.: ÐЦÐÐÐ, 1999, 2001, 2003.
- â Ю. ÐаÑиÑÑевиÑ. ÐеÑÑÑÐ°Ñ Ð¿Ñоблема ÐилÑбеÑÑа. â ÐаÑка, 1993.
ÐиÑеÑаÑÑÑа[ | код]
- ÐиномиалÑнÑе коÑÑÑиÑиенÑÑ // ÐнÑиклопедиÑеÑкий ÑловаÑÑ ÐÑокгаÑза и ÐÑÑона : в 86 Ñ. (82 Ñ. и 4 доп.). â СÐб., 1890â1907.
- ФÑÐºÑ Ð., ФÑÐºÑ Ð. ÐÑиÑмеÑика биномиалÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов // ÐванÑ. â 1970. â â 6. â С. 17â25.
- ÐÑзÑмин Ð. Ð. ТÑеÑголÑник и пиÑамида ÐаÑкалÑ: ÑвойÑÑва и обобÑÐµÐ½Ð¸Ñ // СоÑоÑовÑкий ÐбÑазоваÑелÑнÑй ÐÑÑнал. â 2000. â Т. 6, â 5. â С. 101â109.
- Ðандо С. Ð. Теневое иÑÑиÑление // VIII леÑнÑÑ Ñкола «СовÑÐµÐ¼ÐµÐ½Ð½Ð°Ñ Ð¼Ð°ÑемаÑика». â ÐÑбна, 2008.
- ÐинбеÑг Ð. Ð. УдивиÑелÑнÑе аÑиÑмеÑиÑеÑкие ÑвойÑÑва биномиалÑнÑÑ ÐºÐ¾ÑÑÑиÑиенÑов // ÐаÑемаÑиÑеÑкое пÑоÑвеÑение. â 2008. â ÐÑп. 12. â С. 33â42.
- ÐоналÑд ÐнÑÑ, Роналд ÐÑÑÑ ÐµÐ¼, ÐÑен ÐаÑаÑник. ÐонкÑеÑÐ½Ð°Ñ Ð¼Ð°ÑемаÑика. ÐаÑемаÑиÑеÑкие оÑÐ½Ð¾Ð²Ñ Ð¸Ð½ÑоÑмаÑики = Concrete Mathematics. A Foundation for Computer Science. â 2-е. â Ð.: ÐиÑ; Ðином. ÐабоÑаÑоÑÐ¸Ñ Ð·Ð½Ð°Ð½Ð¸Ð¹; «ÐилÑÑмÑ», 1998 â 2009. â 703, 784 Ñ. â ISBN 95-94774-560-7, 78-5-8459-1588-7.
