Каким свойством обладают противоположные грани параллелепипеда

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
Что такое параллелепипед
Что за слово такое мудреное – «параллелепипед»? Что за многогранник скрывается за этим словом? Что-то должно быть связано с параллельностью, не правда ли?
Так и есть:

Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Основные понятия
Смотри, запоминай и не путай!






Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
Свойства параллелепипеда
- Все грани параллелепипеда – параллелограммы.
- Противоположные грани параллелепипеда параллельны и равны.

Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, а смежные.
- Боковые ребра параллелепипеда равны:



- Диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.

Точка пересечения диагоналей называется центром параллелепипеда.
Прямой параллелепипед
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
Вот так:

У прямого параллелепипеда в основании – параллелограмм, а боковые грани — прямоугольники.
Прямоугольный параллелепипед
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:

У прямоугольного параллелепипеда все грани – прямоугольники.
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

.
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Смотри:

— прямоугольный, поэтому
— тоже прямоугольный!
Поэтому
,
Подставим:
Вывели формулу.
Куб
Куб – параллелепипед, у которого все грани квадраты.

Все ребра куба равны.
Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.
Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.
,
То есть
Давай убедимся в пользе этой формулы.
Представь, что у тебя задача: «Диагональ куба равна . Найти полную поверхность».
Пользуясь нашей формулой: , мы узнали, что , то есть .
Значит полная поверхность – шесть площадей квадратов со стороной -равна:
.
Видишь как быстро? И ты применяй!
ПАРАЛЛЕЛЕПИПЕД. КУБ. КОРОТКО О ГЛАВНОМ
1. Определения:
 | Параллелепипед — это четырехугольная призма (многогранник с гранями), все грани которой — параллелограммы. |
 | Прямой параллелепипед — это параллелепипед, у которого боковые грани — прямоугольники. |
 | Прямоугольный параллелепипед — параллелепипед, у которого все грани — прямоугольники |
 | Куб – параллелепипед, у которого все грани квадраты. |
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
2. Свойства:
- Противолежащие грани параллелепипеда параллельны и равны.
- Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через точку пересечения диагоналей (центр параллелепипеда), делится ею пополам.
- Все диагонали прямоугольного параллелепипеда равны между собой и равны сумме квадратов его измерений.
.

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Параллелепи́пед др.-греч. παραλληλ-επίπεδον[1] от др.-греч. παρ-άλληλος — «параллельный» и др.-греч. ἐπί-πεδον — «плоскость») — четырёхугольная призма, основанием которой служит параллелограмм, или, что равносильно, многогранник, у которого шесть граней, каждая из которых — параллелограмм.
Типы параллелепипеда[править | править код]
Прямоугольный параллелепипед
Различается несколько типов параллелепипедов:
- Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники.
- Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани прямоугольники.
- Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.
- Ромбоэдр — параллелепипед, грани которого являются равными ромбами.
- Куб — параллелепипед, грани которого являются квадратами.
Основные элементы[править | править код]
Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро — смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.
Свойства[править | править код]
- Параллелепипед симметричен относительно середины его диагонали.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Противолежащие грани параллелепипеда параллельны и равны.
- Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.
Основные формулы[править | править код]
Прямой параллелепипед[править | править код]
Площадь боковой поверхности
Sб=Ро*h, где Ро — периметр основания, h — высота
Площадь полной поверхности
Sп=Sб+2Sо, где Sо — площадь основания
Объём
V=Sо*h
Прямоугольный параллелепипед[править | править код]
Площадь боковой поверхности
Sб=2c(a+b), где a, b — стороны основания, c — боковое ребро прямоугольного параллелепипеда
Площадь полной поверхности
Sп=2(ab+bc+ac)
Объём
V=abc, где a, b, c — измерения прямоугольного параллелепипеда.
Куб[править | править код]
Площадь поверхности:
Объём: , где — ребро куба.
Произвольный параллелепипед[править | править код]
Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель Грама указанных трёх векторов равен квадрату их смешанного произведения[2]:215.
В математическом анализе[править | править код]
В математическом анализе под n-мерным прямоугольным параллелепипедом понимают множество точек вида
Сечение параллелепипеда плоскостью[править | править код]
В зависимости от расположения секущей плоскости и параллелепипеда сечение параллелепипеда может быть треугольником, четырехугольником, пятиугольником и шестиугольником.
Примечания[править | править код]
Ссылки[править | править код]
- Прямоугольный параллелепипед
Тетраэдр. Виды тетраэдров
Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).
Рис. 1
У тетраэдра (4) грани, (4) вершины и (6) рёбер (Рис. 1).
Один из треугольников называется основанием тетраэдра, а три остальные — боковыми гранями тетраэдра.
В зависимости от видов треугольников и их расположения выделяют разные виды тетраэдров.
В школьном курсе чаще говорят о следующих видах тетраэдра:
— равногранный тетраэдр, у которого все грани — равные между собой треугольники;
— правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);
— правильный тетраэдр, у которого все четыре грани — равносторонние треугольники (Рис. 2).
Рис. 2 Рис. 3
Свойство правильного тетраэдра:
из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.
Параллелепипед. Виды параллелепипедов
Параллелепипедом называется многогранник, у которого (6) граней — параллелограммы.
Рис. 4
У параллелепипеда, как отмечено, (6) граней, (8) вершин и (12) рёбер (Рис. 4).
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер — противоположными.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.
Рёбра параллелепипеда, не принадлежащие основаниям, называют боковыми рёбрами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (Рис. 5).
Рис. 5
В зависимости от видов параллелограммов и их расположения выделяют разные виды параллелепипедов:
параллелепипеды могут быть прямые и наклонные.
У прямых параллелепипедов боковые грани — прямоугольники (Рис. 5),
у наклонных — параллелограммы (Рис. 4).
Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.
Рис. 6
Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
У прямоугольного параллелепипеда — три линейных размера: DA, DC, DD1 (Рис. 6).
Свойства параллелепипеда:
— противоположные грани параллелепипеда равны и параллельны.
— Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
— Боковые грани прямого параллелепипеда — прямоугольники.
Построение сечения тетраэдра и параллелепипеда
Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.
Секущая плоскость пересекает грани многогранников по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Так как у тетраэдра (4) грани, то сечением тетраэдра может быть треугольник (Рис. 7) или
четырёхугольник (Рис. 8).
Рис. 7 Рис. 8
У параллелепипеда (6) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).
При построении сечения надо вспомнить следующие знания из предыдущих тем:
1. если две точки прямой принадлежат плоскости, то прямая находится в этой плоскости.
2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.
3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны.
Пример:
Задача
Построить сечение параллелепипеда плоскостью, которая проходит через точки (K), (M) и (N).
1. Проводим (MK), так как обе точки находятся в одной плоскости;
2. MK∩CC1=X — непараллельные прямые в одной плоскости пересекаются;
3. проводим (XN), так как обе точки находятся в одной плоскости;
4. XN∩D1C1=P;
5. проводим (MP), так как обе точки находятся в одной плоскости;
6. через точку (N) в плоскости основания NL∥MP, так как линии пересечения параллельных плоскостей с третьей плоскостью должны быть параллельны;
7. соединяем (N) и (L) и получаем сечение (MPNLK).
Определение
Многогранником будем называть замкнутую поверхность, составленную из многоугольников и ограничивающую некоторую часть пространства.
Отрезки, являющиеся сторонами этих многоугольников, называются ребрами многогранника, а сами многоугольники – гранями. Вершины многоугольников называются вершинами многогранника.
Будем рассматривать только выпуклые многогранники (это такой многогранник, который находится по одну сторону от каждой плоскости, содержащей его грань).
Многоугольники, из которых составлен многогранник, образуют его поверхность. Часть пространства, которую ограничивает данный многогранник, называется его внутренностью.
Определение: призма
Рассмотрим два равных многоугольника (A_1A_2A_3…A_n) и (B_1B_2B_3…B_n), находящихся в параллельных плоскостях так, что отрезки (A_1B_1, A_2B_2, …, A_nB_n) параллельны. Многогранник, образованный многоугольниками (A_1A_2A_3…A_n) и (B_1B_2B_3…B_n), а также параллелограммами (A_1B_1B_2A_2, A_2B_2B_3A_3, …), называется ((n)-угольной) призмой.
Многоугольники (A_1A_2A_3…A_n) и (B_1B_2B_3…B_n) называются основаниями призмы, параллелограммы (A_1B_1B_2A_2, A_2B_2B_3A_3,
…) – боковыми гранями, отрезки (A_1B_1, A_2B_2, …, A_nB_n) – боковыми ребрами.
Таким образом, боковые ребра призмы параллельны и равны между собой.
Рассмотрим пример — призма (A_1A_2A_3A_4A_5B_1B_2B_3B_4B_5), в основании которой лежит выпуклый пятиугольник.
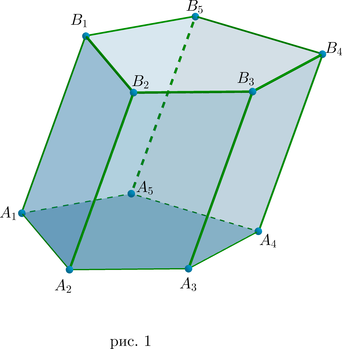
Высота призмы – это перпендикуляр, опущенный из любой точки одного основания к плоскости другого основания.
Если боковые ребра не перпендикулярны основанию, то такая призма называется наклонной (рис. 1), в противном случае – прямой. У прямой призмы боковые ребра являются высотами, а боковые грани – равными прямоугольниками.
Если в основании прямой призмы лежит правильный многоугольник, то призма называется правильной.
Определение: понятие объема
Единица измерения объема – единичный куб (куб размерами (1times1times1) ед(^3), где ед — некоторая единица измерения).
Можно сказать, что объем многогранника – это величина пространства, которую ограничивает этот многогранник. Иначе: это величина, числовое значение которой показывает, сколько раз единичный куб и его части вмещаются в данный многогранник.
Объем имеет те же свойства, что и площадь:
1. Объемы равных фигур равны.
2. Если многогранник составлен из нескольких непересекающихся многогранников, то его объем равен сумме объемов этих многогранников.
3. Объем – величина неотрицательная.
4. Объем измеряется в см(^3) (кубические сантиметры), м(^3) (кубические метры) и т.д.
Теорема
1. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.
Площадь боковой поверхности — сумма площадей боковых граней призмы.
2. Объем призмы равен произведению площади основания на высоту призмы: [V_{text{призмы}}=S_{text{осн}}cdot h]
Определение: параллелепипед
Параллелепипед – это призма, в основании которой лежит параллелограмм.
Все грани параллелепипеда (их (6): (4) боковые грани и (2) основания) представляют собой параллелограммы, причем противоположные грани (параллельные друг другу) представляют собой равные параллелограммы (рис. 2).
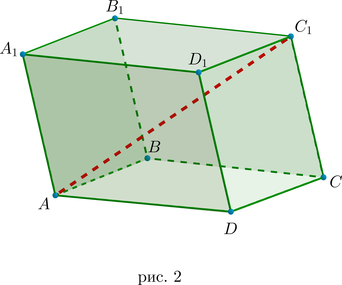
Диагональ параллелепипеда – это отрезок, соединяющий две вершины параллелепипеда, не лежащие в одной грани (их (8): (AC_1,
A_1C, BD_1, B_1D) и т.д.).
Прямоугольный параллелепипед — это прямой параллелепипед, в основании которого лежит прямоугольник.
Т.к. это прямой параллелепипед, то боковые грани представляют собой прямоугольники. Значит, вообще все грани прямоугольного параллелепипеда – прямоугольники.
Все диагонали прямоугольного параллелепипеда равны (это следует из равенства треугольников (triangle ACC_1=triangle AA_1C=triangle
BDD_1=triangle BB_1D) и т.д.).
Замечание
Таким образом, параллелепипед обладает всеми свойствами призмы.
Теорема
Площадь боковой поверхности прямоугольного параллелепипеда равна [S_{text{боков.пов-ти прямоуг. пар-да}}=2(a+b)c]
Площадь полной поверхности прямоугольного параллелепипеда равна [S_{text{полн.пов-ти прямоуг. пар-да}}=2(ab+ac+bc)]
Теорема
Объем прямоугольного параллелепипеда равен произведению трех его ребер, выходящих из одной вершины (три измерения прямоугольного параллелепипеда): [V_{text{прямоуг.пар-да}}=abc]
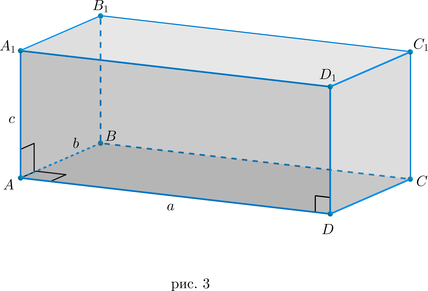
Доказательство
Т.к. у прямоугольного параллелепипеда боковые ребра перпендикулярны основанию, то они являются и его высотами, то есть (h=AA_1=c) Т.к. в основании лежит прямоугольник, то (S_{text{осн}}=ABcdot AD=ab). Отсюда и следует данная формула.
Теорема
Диагональ (d) прямоугольного параллелепипеда ищется по формуле (где (a,b,c) — измерения параллелепипеда) [d^2=a^2+b^2+c^2]
Доказательство
Рассмотрим рис. 3. Т.к. в основании лежит прямоугольник, то (triangle ABD) – прямоугольный, следовательно, по теореме Пифагора (BD^2=AB^2+AD^2=a^2+b^2).
Т.к. все боковые ребра перпендикулярны основаниям, то (BB_1perp
(ABC) Rightarrow BB_1) перпендикулярно любой прямой в этой плоскости, т.е. (BB_1perp BD). Значит, (triangle BB_1D) – прямоугольный. Тогда по теореме Пифагора (B_1D=BB_1^2+BD^2=a^2+b^2+c^2), чтд.
Определение: куб
Куб — это прямоугольный параллелепипед, все грани которого – равные квадраты.
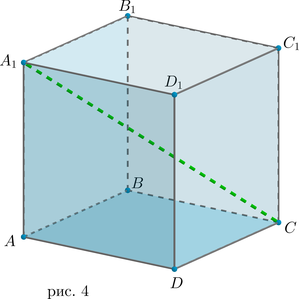
Таким образом, три измерения равны между собой: (a=b=c). Значит, верны следующие
Теоремы
1. Объем куба с ребром (a) равен (V_{text{куба}}=a^3).
2. Диагональ куба ищется по формуле (d=asqrt3).
3. Площадь полной поверхности куба (S_{text{полн.пов-ти
куба}}=6a^2).
Ïàðàëëåëåïèïåä — ïðèçìà, îñíîâàíèåì êîòîðîé ÿâëÿåòñÿ ïàðàëëåëîãðàìì ëèáî (ðàâíîñèëüíî) ìíîãîãðàííèê ñ øåñòüþ ãðàíÿìè, ÿâëÿþùèìèñÿ ïàðàëëåëîãðàììàìè. Øåñòèãðàííèê.
Ïàðàëëåëîãðàììû, èç êîòîðûõ ñîñòîèò ïàðàëëåëåïèïåä ÿâëÿþòñÿ ãðàíÿìè ýòîãî ïàðàëëåëåïèïåäà, ñòîðîíû ýòèõ ïàðàëëåëîãðàììîâ ÿâëÿþòñÿ ðåáðàìè ïàðàëëåëåïèïåäà, à âåðøèíû ïàðàëëåëîãðàììîâ — âåðøèíàìè ïàðàëëåëåïèïåäà. Ó ïàðàëëåëåïèïåäà êàæäàÿ ãðàíü ÿâëÿåòñÿ ïàðàëëåëîãðàììîì.
Êàê ïðàâèëî âûäåëÿþò ëþáûå 2-å ïðîòèâîëåæàùèå ãðàíè è íàçûâàþò èõ îñíîâàíèÿìè ïàðàëëåëåïèïåäà, à îñòàâøèåñÿ ãðàíè — áîêîâûìè ãðàíÿìè ïàðàëëåëåïèïåäà. Ðåáðà ïàðàëëåëåïèïåäà, êîòîðûå íå ïðèíàäëåæàò îñíîâàíèÿì ÿâëÿþòñÿ áîêîâûìè ðåáðàìè.
2 ãðàíè ïàðàëëåëåïèïåäà, êîòîðûå èìåþò îáùåå ðåáðî ÿâëÿþòñÿ ñìåæíûìè, à òå, êîòîðûå íå èìåþò îáùèõ ðåáåð — ïðîòèâîïîëîæíûìè.
Îòðåçîê, êîòîðûé ñîåäèíÿåò 2 âåðøèíû, êîòîðûå íå ïðèíàäëåæàò 1-îé ãðàíè ÿâëÿåòñÿ äèàãîíàëüþ ïàðàëëåëåïèïåäà.
Äëèíû ðåáåð ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà, êîòîðûå íå ïàðàëëåëüíû, ÿâëÿþòñÿ ëèíåéíûìè ðàçìåðàìè (èçìåðåíèÿìè) ïàðàëëåëåïèïåäà. Ó ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà 3 ëèíåéíûõ ðàçìåðà.
Òèïû ïàðàëëåëåïèïåäà.
Ñóùåñòâóåò íåñêîëüêî âèäîâ ïàðàëëåëåïèïåäîâ:
Ïðÿìûì ÿâëÿåòñÿ ïàðàëëåëåïèïåä ñ ðåáðîì, ïåðïåíäèêóëÿðíûì ïëîñêîñòè îñíîâàíèÿ.
Ïðÿìîé ïàðàëëåëåïèïåä ñ ïðÿìîóãîëüíèêîì â îñíîâàíèè ÿâëÿåòñÿ ïðÿìîóãîëüíûì ïàðàëëåëåïèïåäîì. Ó ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà êàæäàÿ èç ãðàíåé ÿâëÿåòñÿ ïðÿìîóãîëüíèêîì.

Íàêëîííûé ïàðàëëåëåïèïåä — ýòî ïàðàëëåëåïèïåä, ó êîòîðîãî áîêîâûå ãðàíè ðàñïîëîæåíû, ïî îòíîøåíèþ ê îñíîâàíèÿì, ïîä óãëîì, íå ðàâíûì 90 ãðàäóñîâ.

Ïðÿìîóãîëüíûé ïàðàëëåëåïèïåä, ó êîòîðîãî âñå 3 èçìåðåíèÿ èìåþò ðàâíóþ âåëè÷èíó, ÿâëÿåòñÿ êóáîì. Êàæäàÿ èç ãðàíåé êóáà – ýòî ðàâíûå êâàäðàòû.
Ïðîèçâîëüíûé ïàðàëëåëåïèïåä. Îáú¸ì è ñîîòíîøåíèÿ â íàêëîííîì ïàðàëëåëåïèïåäå â îñíîâíîì îïðåäåëÿþòñÿ ïðè ïîìîùè âåêòîðíîé àëãåáðû. Îáú¸ì ïàðàëëåëåïèïåäà ðàâíÿåòñÿ àáñîëþòíîé âåëè÷èíå ñìåøàííîãî ïðîèçâåäåíèÿ 3-õ âåêòîðîâ, êîòîðûå îïðåäåëÿþòñÿ 3-ìÿ ñòîðîíàìè ïàðàëëåëåïèïåäà (êîòîðûå èñõîäÿò èç îäíîé âåðøèíû). Ñîîòíîøåíèå ìåæäó äëèíàìè ñòîðîí ïàðàëëåëåïèïåäà è óãëàìè ìåæäó íèìè ïîêàçûâàåò óòâåðæäåíèå, ÷òî îïðåäåëèòåëü Ãðàìà äàííûõ 3-õ âåêòîðîâ ðàâíÿåòñÿ êâàäðàòó èõ ñìåøàííîãî ïðîèçâåäåíèÿ.
Ñâîéñòâà ïàðàëëåëåïèïåäà.
- Ïàðàëëåëåïèïåä ñèììåòðè÷åí îòíîñèòåëüíî ñåðåäèíû åãî äèàãîíàëè.
- Âñÿêèé îòðåçîê ñ êîíöàìè, êîòîðûå ïðèíàäëåæàò ïîâåðõíîñòè ïàðàëëåëåïèïåäà è êîòîðûé ïðîõîäèò ÷åðåç ñåðåäèíó åãî äèàãîíàëè, äåëèòñÿ åþ íà äâå ðàâíûå ÷àñòè. Âñå äèàãîíàëè ïàðàëëåëåïèïåäà ïåðåñåêàþòñÿ â 1-îé òî÷êå è äåëÿòñÿ åþ íà äâå ðàâíûå ÷àñòè.
- Ïðîòèâîïîëîæíûå ãðàíè ïàðàëëåëåïèïåäà ïàðàëëåëüíû è èìåþò ðàâíûå ðàçìåðû.
- Êâàäðàò äëèíû äèàãîíàëè ïðÿìîóãîëüíîãî ïàðàëëåëåïèïåäà ðàâíÿåòñÿ ñóììå êâàäðàòîâ 3-õ åãî èçìåðåíèé.
 ïàðàëëåëåïèïåä âïèñûâàþò òåòðàýäð. Îáúåì ýòîãî òåòðàýäðà áóäåò ðàâíÿòüñÿ òðåòüåé ÷àñòè îáúåìà ïàðàëëåëåïèïåäà.


Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû — ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
| Ïðèçìà ìíîãîãðàííèê, 2 ãðàíè ýòî êîíãðóýíòíûå (ðàâíûå) ìíîãîóãîëüíèêè, êîòîðûå ëåæàò â ïàðàëëåëüíûõ ïëîñêîñòÿõ, à îñòàâøèåñÿ ãðàíè ïàðàëëåëîãðàììû, èìåþùèå îáùèå ñòîðîíû ñ ýòèìè ìíîãîóãîëüíèêàìè. | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
