Каким свойством обладают односторонние углы
С помощью этого видеоурока все желающие смогут получить представление о теме «Параллельные прямые и задачи на углы между ними и секущей». В ходе занятия учащиеся смогут кратко повторить теоретические сведения о параллельных прямых и углах между ними и секущей. Затем применить эти знания, решив несколько задач по соответствующей теме.
Повторение
Параллельными называются такие прямые, которые не пересекаются.
– прямые, с – секущая.
Рис. 1
Возникает много углов (1, 2, 3, 4, 5, 6, 7, 8).
Эти углы важны для нас, и поэтому они имеют названия:
— накрест лежащие углы: ∠3 и ∠5, ∠4 и ∠6;
— односторонние углы: ∠4 и ∠5, ∠3 и ∠6;
— соответственные углы: ∠1 и ∠5, ∠4 и ∠8, ∠2 и ∠6, ∠3 и ∠7.
Основные теоремы о параллельности прямых:
Рис. 2
Если накрест лежащие углы равны, то прямые параллельны. И наоборот, если прямые параллельны, то накрест лежащие углы равны.
Рис. 3
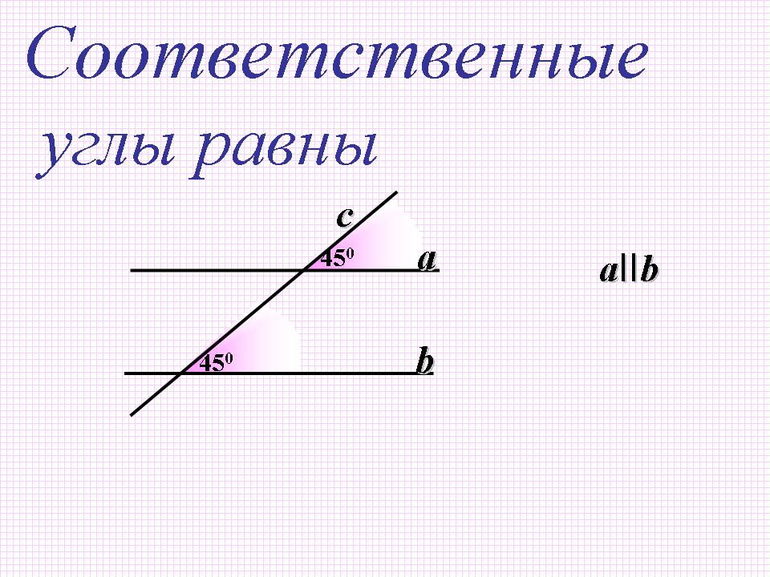
Если соответственные углы равны, то прямые параллельны. И наоборот, если прямые параллельны, то соответственные углы равны.
Рис. 4
Если сумма внутренних углов равна , то прямые параллельны. И наоборот, если прямые параллельны, то сумма внутренних углов равна .
Рассмотрим некоторые типовые задачи на признаки параллельности прямых.
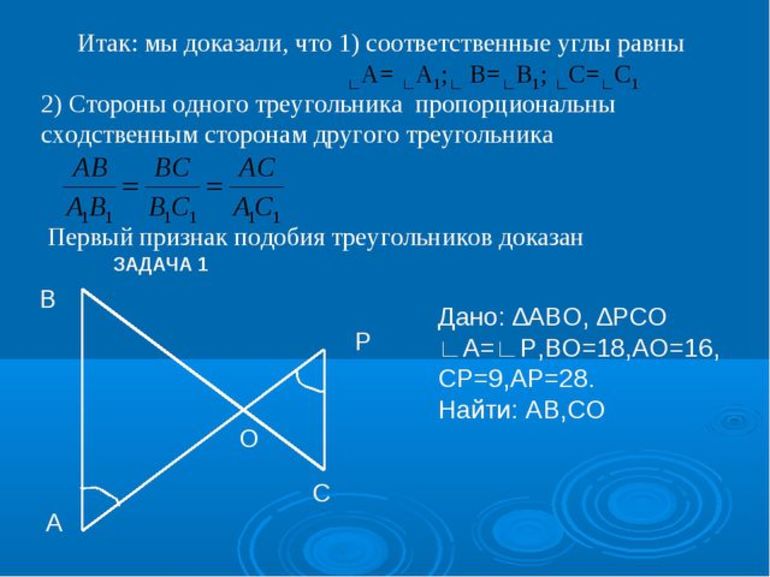
Задача 1
Задача 1:
Сумма накрест лежащих углов при пересечении двух параллельных прямых секущей равна 210. Найдите эти углы.
Дано:.
Найти:.
Рис. 5
Решение:
Поскольку прямые a и b параллельны, то накрест лежащие углы равны.
Следовательно, .
Тогда .
Ответ:.
Задача 2
Задача 2:
Найдите все углы, образованные при пересечении параллельных прямых a и b с секущей c, если:
А. один из углов равен ;
Б. один из углов на больше другого.
Рис. 6
А.
Дано:.
Найти:.
Решение:
1. (как вертикальные);
2. (как смежные);
(как вертикальные);
;
3. и (как соответственные)
и (как вертикальные)
Ответ:, .
Б.
Дано:.
Найти:.
Решение:
1.
+
, .
Тогда .
2. и (как соответственные)
и (как вертикальные)
Ответ:, .
Задача 3
Задача 3:
На рисунке , прямые m и n – биссектрисы углов 1 и 2. Докажите, что .
Рис. 7
Доказательство:
Из того, что , по свойству параллельных прямых вытекает, что .
Следовательно, углы 3, 4, 5, 6 тоже будут равны между собой, как половинки равных углов.
Тогда из того, что , по первому признаку параллельности прямых , что и требовалось доказать.
Список рекомендованной литературы
- Александров А.Д., Вернер А.Л., Рыжик В.И. и др. Геометрия 7. – М.: Просвещение.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 7. 5-е изд. – М.: Просвещение.
- Бутузов В.Ф., Кадомцев С.Б., Прасолова В.В. Геометрия 7 / В.Ф. Бутузов, С.Б. Кадомцев, В.В. Прасолова, под ред. Садовничего В.А. – М.: Просвещение, 2010.
Рекомендованные ссылки на интернет-ресурсы
- Признаки параллельности прямых (Источник).
- Признаки параллельности двух прямых (Источник).
Рекомендованное домашнее задание
- Докажите, что биссектрисы соответственных углов при параллельных прямых параллельны.
- Две параллельные прямые пересечены третьей прямой так, что сумма двух из полученных восьми углов равна 240. Найдите меры всех образованных углов.
- Через точку, не лежащую на прямой a, проведено три прямые. Докажите, что по крайней мере две из них пересекают прямую a.
Базисные понятия
Угол — простая фигура в геометрии, образуемая двумя лучами, следующими из некоторой точки. Эту точку определяют как его вершину. Название «угол» может относиться к части плоскости, объединяющей все лучи, исходящие из вершины фигуры. Такое обозначение может также иметь угловая мера, чаще всего определяемая в градусах.
В геометрии существует несколько критериев, позволяющих выделить разные типы угловых фигур. Они бывают тупыми и острыми, смежными или вертикальными. Для углов, образуемых в результате пересечения секущей линией двух прямых, в качестве такого критерия берется свойство взаимных соотношений формируемых при этом фигур. При рассмотрении произвольного геометрического рисунка, образованного двумя прямыми линиями и секущей, можно увидеть 4 пары соответственных, по 2 пары внутренних и внешних накрест лежащих или односторонних угловых фигур. Все эти элементы могут быть как тупоугольными, так и остроугольными.
Углы, образующиеся при пересечении прямых
Чтобы понять, как выглядят соответственные углы, а также уметь находить их на любых геометрических рисунках, нужно хорошо усвоить разницу между типами фигур, образованных секущей линией. Кроме того, следует обратить внимание на наличие внутренней и внешней областей. Первая зона ограничивается площадью между двумя прямыми, второй внешней областью считается неограниченное пространство снаружи от этих двух линий.
Итак, образованным тремя прямыми линиями угловым фигурам можно дать следующие определения:
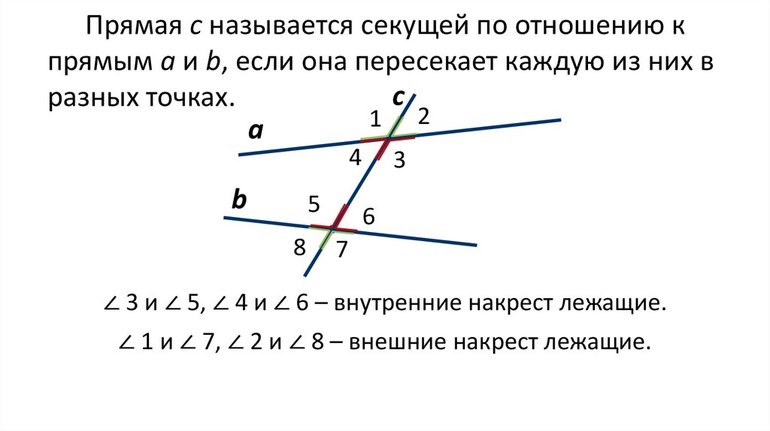
- Накрест лежащие внутренние углы — это разносторонние по отношению к секущей объекты внутри области, сформированной прямыми. Если обе фигуры лежат за пределами двух прямых по противоположные стороны от секущей, то такие угловые элементы называются внешними накрест лежащими.
- В отличие от предыдущих противолежащих фигур, односторонние углы расположены на одной стороне: внутри области, образованной двумя прямыми (внутренние), или во внешних областях (наружные).
- Соответственные по определению являются парными фигурами, образующимися по одну сторону от линии, пересекающей две других, с аналогичных сторон обеих прямых. Один из углов пары расположен между прямыми и является внутренним, а другой лежит вне этой зоны, поэтому считается внешним.
Более наглядное представление об этом типе углов можно получить, если секущую изобразить в виде направленного вектора. Парные угловые элементы расположены в одном направлении относительно прямых, пересеченных третьей линией.
Чтобы окончательно разобраться в вопросе, нужно усвоить понятие соответствия с математической точки зрения. В геометрии это свойство двух фигур, у которых углы, стороны или точки одного объекта аналогичны соответствующим элементам другого объекта. Аналогия проявляется не в их равенстве, а во взаимном соотношении элементов. О соответствии углов говорит аналогичное пространственное положение лучей в местах пересечения прямых с третьей секущей линией. Таким образом, речь идет об элементах, имеющих одинаковое относительное положение.
Соответственные углы при параллельных прямых
Свойства фигур, формирующихся при пересечении секущей параллельных прямых, давно описаны в планиметрии. Известно, что соответственные накрест лежащие угловые элементы при параллельных прямых равны. Сложение угловых величин односторонних фигур дает значение 180 градусов. В геометрии применяется формула для расчета суммы соответственных парных угловых фигур при условии параллельности двух линий. Для определения этого параметра из числа 360 надо вычесть удвоенную угловую величину одностороннего угла, прилежащего к любому из пары рассчитываемых соответственных угловых элементов.

Равные соответственные углы указывают на параллельность прямых. Справедливость этого признака вытекает из следующих утверждений:

- Отметим отрезок на секущей, начало и конец которого, точки C и D, находятся в местах пересечения секущей с прямыми a и b.
- Через среднюю точку K отрезка опустим перпендикуляр к прямой a. Точки его пересечения с прямыми обозначим как A и B. Сформированные отрезками треугольники CKA и DKB являются прямоугольными, а отрезки AK и BK — сторонами, прилежащими к прямоугольным вершинам. Каждый из этих катетов одновременно является высотой треугольника, проведенной из остроугольной вершины.
- Для доказательства следует учитывать равенство вертикальных ∠CKA и ∠DKB, ∠BDK и ∠АСК равны по условию равенства соответственных углов с учетом того, что вертикальные углы с вершинами в точках C и D равны, CK и KD — два равных отрезка по условию.
- Таким образом, в треугольниках CKA и DKB сторона и прилежащие к ней углы имеют равные величины, что соответствует одному из признаков равенства треугольников.
- Поскольку AB перпендикулярен прямой a и отрезку AC, то CKA — прямоугольный треугольник, и это дает основание считать, что равный ему треугольник DKB также прямоугольный, из чего следует перпендикулярность отрезка AB по отношению к прямой b.
- Было доказано, что две прямые перпендикулярны к третьей прямой, и это подтверждает их параллельность.
Доказательство можно развернуть и в обратном направлении. Параллельные линии при пересечении третьей прямой формируют одинаковые по величине соответственные углы. Это утверждение известно как свойство параллельных линий.
Такого рода свойства встречаются в описаниях признаков и теорем. Их равенство — часть доказательств равенства и подобия треугольников. В свою очередь, используя признаки подобных и равных треугольников, можно обосновывать доказательства сложных теорем, находить решения сложных задач, править возможные ошибки.
Доказательство подобия треугольников
Существует три признака, по которым могут быть определены подобные треугольники. Во-первых, подобие подтверждается пропорциональностью всех трех сторон треугольников. Во-вторых, подобными считаются треугольники, имеющие две пропорциональные стороны, угловая величина между которыми равна соответствующему элементу второго треугольника. В-третьих, подобие подтверждается, когда имеет место равенство двух углов обоих треугольников.
Рассмотрим доказательство этого признака, в ходе которого применяется свойство тождественности соответственных угловых объектов:

- Возьмем два треугольника ABC и A1B1C1, в которых равны два угла. Из этого следует, что величина третьего угла также одинакова в обеих фигурах. Требуется доказать подобие треугольников.
- Отметим точку A2 на AB таким образом, чтобы величина BA2 совпала с A1B1. Через A2 параллельно основанию AC проведем прямую, проходящую через BC в точке B2.
- Треугольники A2BC2 и A1B1C1 равны, что подтверждается одинаковыми величинами сторон A1B1, BA2 и углов B, B1 (по построению или условию), а также равенством углов A, A1 как соответственных при параллельных линиях.
- Поскольку, согласно лемме, параллельная стороне треугольника прямая отсекает от него подобный треугольник, то A2BC2 подобен ABC. Из этого следует подобие треугольников ABC и A1B1C1.
Подобного рода рассуждения и доказательства, учитывающие свойства соответственных угловых фигур, учитываются при решении разного рода задач.
В сложных планиметрических фигурах в качестве секущей, формирующей этот тип геометрических объектов, может выступать медиана, биссектриса треугольника или какие-либо другие линии. Для решения таких задач требуется хорошее знание базовых понятий, признаков, свойств, аксиом, позволяющее заметить определенные соотношения и закономерности в том или ином задании.
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Стороны угла – лучи, которые образуют угол.
Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.
Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB или ∠BOA, но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.
Величину угла измеряют в градусах. ∠AOB=24°.
Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.
Или
Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.
OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.
∠AOD=∠BOD=∠AOB2
Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.
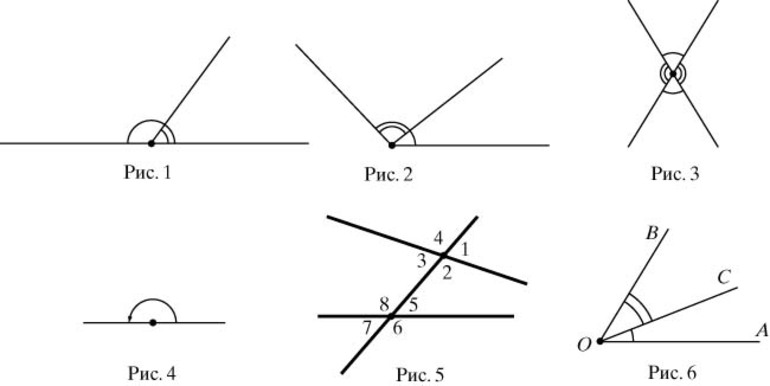
Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.
Свойство: вертикальные углы равны.
Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.
Свойство: сумма смежных углов равна 180°.
Пример:
Пары углов
(1) и (3)
(2) и (4)
называются вертикальными.
По свойству вертикальных углов:
∠COD=∠AOB
∠BOD=∠AOC
Пары углов
(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)
называются смежными.
По свойству смежных углов:
∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°
Прямая, пересекающая две заданные прямые, называется секущей этих прямых.
Существует пять видов углов, которые образуются при пересечении двух прямых секущей.
Пары углов:
(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)
называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).
Пары углов:
(3) и (5)
(4) и (6)
называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).
Пары углов:
(1) и (7)
(2) и (8)
называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).
Пары углов:
(3) и (6)
(4) и (5)
называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).
Пары углов:
(1) и (8)
(2) и (7)
называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).
Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:
- Соответственные углы равны.
- Внутренние накрест лежащие углы равны.
- Внешние накрест лежащие углы равны.
- Сумма внутренних односторонних углов равна 180°.
- Сумма внешних односторонних углов равна 180°.
Сумма углов произвольного n-угольника вычисляется по формуле:
Sn=180°⋅(n−2)
где n – это количество углов в n-угольнике.
Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.
Сумма углов треугольника: S3=180°⋅(3−2)=180°
Сумма углов четырехугольника: S4=180°⋅(4−2)=360°
Сумма углов пятиугольника: S5=180°⋅(5−2)=540°
Так можно продолжать до бесконечности.
Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.
На рисунках изображены примеры правильных многоугольников:
Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.
αn=180°⋅(n−2)n
Модуль геометрия: задания, связанные с углами
Скачать домашнее задание к уроку 2.
