Каким свойством обладают диагонали параллелограмма

Самое интересное в истории с гипотезой Пуанкаре, — не кто и как, а что именно. Григорий Перельман справился с большей проблемой, а гипотеза Пуанкаре получилась как простое следствие (и не самое значительное) из его работы.
К концу XIX века уже были известны топологические типы двумерных «хороших» поверхностей. Довольно трудно объяснить, какие поверхности «хорошие», но я нарисую кое-что нехорошее:
У поверхности окрестность любой точки должна быть похожа на диск. Под номером 1 – не поверхность, ведь у выделенной точки ближайшая окрестность – трехлепестковая штучка, а не просто диск. Хорошая поверхность должна быть связной, безграничной и конечной
Хорошие поверхности уже можно классифицировать.
Скажем, поверхности мяча, бублика и кренделя – разных типов, непрерывными преобразованиями нельзя одну деформировать в другую. Непрерывно деформировать – значит растягивать, сжимать и скручивать, но только не рвать и не склеивать кусочки.
Здесь важно, что мы, жители 3-мерного пространства, с одного взгляда отличаем эти поверхности. А что же их плоские обитатели, которые не могут выбраться в третье измерение? Им было бы непросто разобраться, что представляет собой мир, в котором они живут. Скажем, муравей, который живет на бублике, не видит дырки от бублика – он воспринимает только двумерную поверхность, на которой живет. Но муравей может расположить на поверхности веревочную петлю, которую невозможно стянуть в точку. Так он и определит, что живет не на сфере, ведь на сфере любая петля в точку стягивается.
Нам, обычным трехмерным жителям привычного трехмерного пространства, тоже непросто разобраться, что представляет собой мир, в котором мы живем! Мы не можем выбраться в следующее измерение, чтобы посмотреть на наш мир снаружи. Придется научиться характеризовать трехмерный мир по его внутренней природе, а не по тому, как он вписывается в гипотетическое следующее измерение.
В начале XX века Анри Пуанкаре хотел разобраться с трехмерными многообразиями (аналогами поверхностей). Он высказал обманчиво простое утверждение:
если на трехмерном многообразии (без границы, конечном) любой контур стягивается в точку, оно должно быть топологически эквивалентно 3-мерной сфере.
3-мерная сфера – непростой объект. Возьмем двумерный диск в виде гибкой пленки с границей в виде гибкого шнурка. Продавим диск, чтобы получился этакий мешок, а потом стянем шнурок-границу в точку. Получим 2-мерную сферу, на которую мы смотрим из трехмерного пространства. Теперь сделаем то же самое с трехмерным диском (обычно мы называем трехмерный диск шаром). Стянем его границу в точку и получим 3-мерную сферу. Говорят, есть такие люди, которые могут это с легкостью представить.
Эту гипотезу можно обобщить; обобщенная гипотеза Пуанкаре говорит примерно то же самое, но только для размерностей выше 3. И вот для больших (больше 4) размерностей ее доказал в 1960-1970-х годах прошлого века Стивен Смейл (он составлял список задач XXI века и поместил в него гипотезу Пуанкаре).
Для размерности 4 доказательство придумал Марк Фридман в 1982 году. И только родная, домашняя размерность 3 никак не поддавалась.
Тем временем топология не стояла на месте. Уильям Тёрстон придумал способ классифицировать все трехмерные многообразия. Это куда круче, чем характеризовать одну только 3-мерную сферу. Он придумал разбивать любое трехмерное многообразие на куски, на каждом из которых реализуется одна из восьми стандартных геометрий. На помощь топологии Тёрстон призвал геометрию с такими элементами как расстояния и углы – топология обычно их и не рассматривает. Так возникла программа геометризации Тёрстона – охарактеризовать каждое трехмерное многообразие набором геометрий на нем. Гипотеза Пуанкаре стала бы просто следствием этой программы.
В 1982 году Ричард Гамильтон придумал новый метод в геометрическом анализе – потоки Риччи. Этот метод позволял преобразовывать метрику пространства: там, где кривизна отрицательная, — увеличить, там, где большая положительная, — уменьшить. И если исходное многообразие было похоже на сферу, оно в сферу и превратится.
Но с этими потоками Риччи была такая беда: при таком преобразовании иногда возникали особенности. Особенности мешали потокам течь куда надо, и тогда Билл Браудер и Джон Милнор придумали метод хирургии: надо разрезать сингулярность и заклеить потом места разреза. К несчастью, эти сингулярности иногда ведут себя как многоголовая гидра – от одной избавляешься, а несколько появляются.
Гамильтон все же сумел применить методику потоков Риччи так, чтобы провести классификацию двумерных поверхностей. Это показало силу метода, но не более: двумерные поверхности были классифицированы задолго до того. Но и в размерности три Гамильтон смог продвинуться очень далеко. Он открыл новый путь в математике, хотя и не прошел по нему до конца.
Справиться с гидрой сингулярностей смог Григорий Перельман: он показал, что сингулярности не будут множиться бесконечно, рано или поздно они прекратятся. В первой из трех статей по предмету Перельман прямо писал, что дает краткий набросок доказательства гипотезы геометризации (Тёрстона).
После были ещё статьи и долгое их обсуждение в математическом сообществе. Что же сделал Перельман? Доказывал ли он гипотезу Пуанкаре?
На самом деле он справился с трудностями метода потоков Риччи и тем самым доказал гипотезу геометризации Тёрстона. И в качестве приятного бонуса отсюда следовала истинность гипотезы Пуанкаре. Вот за этот бонус и полагалась миллионная премия института Клэя, а вовсе не за основной результат.
Перельман отказался от премии в миллион долларов за доказательство гипотезы Пуанкаре. И объяснял это, в частности, тем, что основная работа сделана не им. Журналисты не могли пройти мимо и не написать о Перельмане; по дороге выяснилось, что способ жизни Перельмана очень своеобразный, и это стало другим поводом о нем писать. Фотографии и детали личной жизни привлекали внимание читателей гораздо больше, чем смысл его работы.
А если бы Перельман взял миллион? Из этого хайп сделать было бы еще проще: обвинить его в том, что Перельман забрал премию, хотя основную работу сделал Гамильтон. И все, до конца дней не отмылся бы.
Параллелограмм.
Приступаем к изучению разных видов четырёхугольников.
Определение. Параллелограммом называется выпуклый четырёхугольник, у которого стороны попарно параллельны.

– параллелограмм. У него .
Рассмотрим свойства параллелограмма.
ТЕОРЕМА. У параллелограмма противолежащие стороны и углы равны.

Дано: – параллелограмм
Доказать:
Доказательство.
1. Проведём диагональ . Рассмотрим и .
2. и ; и – внутренние односторонние при параллельных прямых, значит,
.
3. Итак, , ч.т.д.
ТЕОРЕМА. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Дано: – параллелограмм
и – диагонали
Доказать:
Доказательство.
1. Т.к. параллелограмм является выпуклым четырёхугольником, то, по свойству выпуклых многоугольников, его диагонали пересекаются, т.е. .
2. Рассмотрим и .
по II признаку равенства треугольников , ч.т.д.
Итак, параллелограмм обладает двумя свойствами:
Противолежащие стороны и углы параллелограмма равны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Признаки параллелограмма.
Часто бывает ситуация, когда известны какие-то свойства четырёхугольника, а какой вид имеет этот четырёхугольник неизвестно. В этом случае помогут признаки параллелограмма.
ТЕОРЕМА (I признак параллелограмма).
Если в четырёхугольнике две стороны равны и параллельны, то такой четырёхугольник является параллелограммом.

Дано: – четырёхугольник
Доказать: – параллелограмм.
Доказательство.
Проведём диагональ и рассмотрим и .
. Эти углы являются внутренними накрест лежащими при прямых и , значит, по признаку параллельности прямых, .
Итак, в четырёхугольнике , т.е. стороны попарно параллельны, значит, – параллелограмм (по определению), ч.т.д.
ТЕОРЕМА (II признак параллелограмма).
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник является параллелограммом.

Дано: – четырёхугольник
Доказать: – параллелограмм.
Доказательство.
Проведём диагональ и рассмотрим и .
и . А эти пары углов являются внутренними накрест лежащими. По признаку параллельных прямых: «если внутренние накрест лежащие углы равны, то прямые параллельны», делаем вывод, что , а . По определению параллелограмма, данный четырёхугольник является параллелограммом, ч.т.д.
ТЕОРЕМА (III признак параллелограмма).
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник является параллелограммом.

Дано: – четырёхугольник,
и – диагонали, ,
Доказать: – параллелограмм.
Доказательство.
Рассмотрим и .
по I признаку равенства треугольников и . А эти углы являются внутренними накрест лежащими при прямых и , значит, .
Мы доказали, что в четырёхугольнике две стороны параллельны и равны (), значит, по I признаку, этот четырёхугольник является параллелограммом, ч.т.д.
Начертите параллелограмм . Проведите в нём диагонали и . Обозначьте их точку пересечения буквой .
Найдите длину отрезка , если известно, что диагональ см.
Чему равна диагональ , если известно, что отрезок см?
Найдите периметр треугольника , если сторона равна см, а диагонали и равны см и см соответственно.
Две стороны параллелограмма равны см и см. Найдите периметр параллелограмма.
Сумма двух противолежащих углов параллелограмма равна . Чему равны эти углы?
Периметр параллелограмма равен см. Одна из его сторон равна см. Определите остальные стороны параллелограмма.
Найдите углы параллелограмма, если известно, что один из них равен сумме двух других углов параллелограмма.
Одна из сторон параллелограмма равна см, а другая – в раза меньше. Найдите периметр параллелограмма.
Высоты параллелограмма равны см и см. Найдите расстояние от точки пересечения диагоналей параллелограмма до одной из меньших сторон.
В параллелограмме сторона см, диагонали равны см и см, точка – точка пересечения диагоналей. Чему равен периметр треугольника ?
В параллелограмме один угол равен . Найдите остальные углы параллелограмма.
В треугольнике . Из точки, взятой на стороне , проведены две прямые, параллельные сторонам и . Определите вид получившегося четырёхугольника и все его углы.

Четырёхугольник – параллелограмм, отрезки равны. Докажите, что также является параллелограммом.

Диагональ параллелограмма продолжена на равные отрезки и . Докажите, что также является параллелограммом.
В параллелограмме биссектриса угла пересекает сторону в точке , причём, . Найдите периметр параллелограмма.
Диагональ параллелограмма составляет со сторонами параллелограмма углы в и . Найдите углы параллелограмма.
Стороны параллелограмма относятся как , а его периметр равен см. Найдите стороны параллелограмма.
В четырёхугольнике . Диагонали четырёхугольника пересекаются в точке . Найдите периметр .
Из вершины параллелограмма с острым углом проведён перпендикуляр к прямой . Найдите и .
В выпуклом четырёхугольнике . Докажите, что .
Середина отрезка является центром окружности с диаметром , причём, точки не лежат на одной прямой. Докажите, что .
Постройте параллелограмм по большей стороне, меньшей диагонали и углу между ними.
В четырёхугольнике – точка пересечения диагоналей. Периметр треугольника равен см, см, см. Найдите .
Дан параллелограмм с острым углом . Из вершины опущен перпендикуляр к прямой . Найдите и .
В выпуклом шестиугольнике все стороны равны, . Докажите, что .
Дан параллелограмм . На продолжении диагонали за вершины и отмечены точки и соответственно так, что . Докажите, что .
Постройте параллелограмм по меньшей стороне, острому углу и углу между этой стороной и меньшей диагональю.
Одна сторона параллелограмма втрое больше другой стороны. Найдите стороны параллелограмма, если его периметр равен см.
В параллелограмме с острым углом из вершины проведён перпендикуляр к прямой . Найдите углы параллелограмма, если .
Один из углов параллелограмма на меньше другого. Найдите углы параллелограмма.
В параллелограмме с острым углом из вершины проведён перпендикуляр к прямой . Найдите углы параллелограмма, если .
Докажите, что четырёхугольник, имеющий центр симметрии, является параллелограммом.
На диагонали параллелограмма отмечены две точки и так, что . Докажите, что четырёхугольник – параллелограмм.
На сторонах и параллелограмма вне его построены правильные треугольники и . Докажите, что треугольник равносторонний.
Докажите, что выпуклый четырёхугольник является параллелограммом, если .
Угол параллелограмма меньше угла . Докажите, что .
В параллелограмме проведена биссектриса угла , которая пересекает сторону в точке .
Докажите, что треугольник равнобедренный.
Найдите сторону , если см, а периметр параллелограмма равен см.
На стороне параллелограмма взята точка так, что .
Докажите, что – биссектриса угла .
Найдите периметр параллелограмма, если см, см.
В выпуклом четырёхугольнике диагонали и пересекаются в точке . – медиана треугольника , – медиана треугольника . Докажите, что – параллелограмм.
Прямая параллельна стороне параллелограмма и пересекает стороны и в точках и соответственно. Докажите, что – параллелограмм.
В проведена медиана . На её продолжении за точку отложен отрезок , равный . Докажите, что четырёхугольник является параллелограммом.
Стороны и треугольника продолжены на точку так, что . Докажите, что четырёхугольник – параллелограмм.

– параллелограмм, . Найдите .
Одна из сторон параллелограмма на см больше другой. Периметр параллелограмма равен см. Найдите стороны параллелограмма.
В параллелограмме диагональ перпендикулярна стороне и равна ей. Найдите углы параллелограмма.
Периметр параллелограмма равен см. Найдите длины сторон, если известно, что диагональ параллелограмма делит угол на части и .
В параллелограмме из вершины тупого угла проведена высота к стороне так, что . Найдите углы параллелограмма.
Найдите длины высот параллелограмма, если известно, что стороны см и см, а углы относятся как .
Найдите углы параллелограмма, если известно, что один из них в раз меньше суммы всех остальных углов параллелограмма.
В треугольнике проведена медиана и продолжена на свою длину за точку . Найдите периметр четырёхугольника , если периметр треугольника равен см, см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол . Найдите углы параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите периметр параллелограмма, если см, см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол . Найдите углы параллелограмма.
Периметр параллелограмма равен см. Биссектрисы углов и пересекаются на стороне . Найдите длины сторон параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите углы параллелограмма, если известно, что .
Периметр параллелограмма равен см. Биссектриса угла и биссектриса угла делят сторону на три равные части так, что точка лежит между точками и . Найдите длины сторон параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите углы параллелограмма, если известно, что .
Биссектриса угла параллелограмма пересекает сторону в её середине . Периметр треугольника равен см, а длина отрезка больше стороны на см. Найдите периметр параллелограмма.
6
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
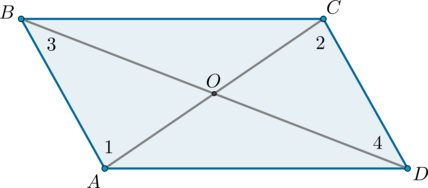
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
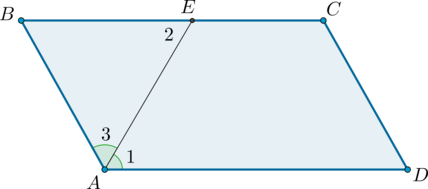
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
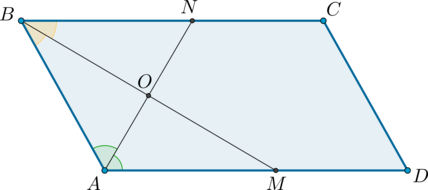
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ — (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).
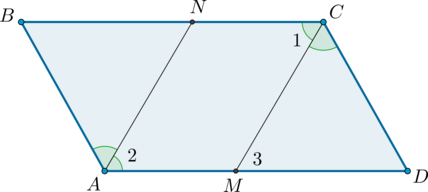
Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).
