Каким свойством обладает вписанный в окружность четырехугольник свойства

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
«Описанная окружность» мы видели, что вокруг всякого треугольника можно описать окружность. То есть, для всякого треугольника найдётся такая окружность, что все три вершины треугольника «сидят» на ней. Вот так:

Вопрос: а можно ли то же самое сказать о четырехугольнике? Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника?
Вот оказывается, что это НЕПРАВДА! НЕ ВСЕГДА четырехугольник можно вписать в окружность. Есть очень важное условие:
 | Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна . |
На нашем рисунке:
Посмотри, углы и лежат друг напротив друга, значит, они противоположные. А что же тогда с углами и ? Они вроде бы тоже противоположные? Можно ли вместо углов и взять углы и ?
Конечно, можно! Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет . Оставшиеся два угла тогда сами собой тоже дадут в сумме . Не веришь? Давай убедимся. Смотри:

Пусть . Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, . То есть — всегда! . Но , → .
Волшебство прямо!
Так что запомни крепко-накрепко:
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна
и наоборот:
Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.
Доказывать всё это мы здесь не будем (если интересно, заглядывай в следующие уровни теории). Но давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна .
Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма? Попробуем сперва «методом тыка».

Вот как-то не получается.
Теперь применим знание:

предположим, что нам как-то удалось посадить на параллелограмм окружность. Тогда непременно должно быть: , то есть .
А теперь вспомним о свойствах параллелограмма:
у всякого параллелограмма противоположные углы равны.
То есть .
У нас получилось, что
→
А что же углы и ? Ну, то же самое конечно.
– вписанный → →
— параллелограмм→ →
Потрясающе, правда?
Получилось, что если параллелограмм вписан в окружность, то все его углы равны , то есть это прямоугольник!

И ещё при этом – центр окружности совпадает с точкой пересечения диагоналей этого прямоугольника. Это, так сказать, в качестве бонуса прилагается.
Ну, вот значит, выяснили, что параллелограмм, вписанный в окружность – прямоугольник.
А теперь поговорим о трапеции. Что будет, если трапецию вписать в окружность? А оказывается, будет равнобедренная трапеция. Почему?

Вот пусть трапеция вписана в окружность. Тогда опять , но из-за параллельности прямых и .
Значит, имеем: → → трапеция равнобокая.
Даже проще чем с прямоугольником, правда? Но запомнить нужно твёрдо – пригодиться: Трапеция, вписанная в окружность – равнобедренная.

Давай ещё раз перечислим самые главные утверждения, касающиеся четырехугольника, вписанного в окружность:
- Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна
- Параллелограмм, вписанный в окружность – непременно прямоугольник и центр окружности совпадает с точкой пересечения диагоналей
- Трапеция, вписанная в окружность – равнобокая.
Вписанный четырехугольник. Средний уровень
Известно, что для всякого треугольника существует описанная окружность (это мы доказывали в теме «Описанная окружность»). Что же можно сказать о четырёхугольнике? Вот, оказывается, что НЕ ВСЯКИЙ четырехугольник можно вписать в окружность, а есть такая теорема:
Четырёхугольник вписан в окружность тогда и только тогда, когда сумма его противоположных углов равна .

На нашем рисунке –
Давай попробуем понять, почему так? Другими словами, мы сейчас докажем эту теорему. Но прежде чем доказывать, нужно понять, как устроено само утверждение. Ты заметил в утверждении слова «тогда и только тогда»? Такие слова означают, что вредные математики впихнули два утверждения в одно.
Расшифровываем:
- «Тогда» означает: Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна .
- «Только тогда» означает: Если у четырёхугольника найдутся два противоположных угла, сумма которых равна , то такой четырехугольник можно вписать в окружность.
Прямо как у Алисы: «думаю, что говорю» и «говорю, что думаю».
А теперь разбираемся, отчего же верно и 1, и 2?
Сначала 1.
Пусть четырехугольник вписан в окружность. Отметим её центр и проведём радиусы и . Что же получится? Помнишь ли ты, что вписанный угол вдвое меньше соответствующего центрального? Если помнишь – сейчас применим, а если не очень – загляни в тему «Окружность. Вписанный угол».

Итак,
— вписанный
— вписанный
Но посмотри: .
Значит,
.
Получаем, что если – вписанный, то
.
Ну, и ясно, что и тоже в сумме составляет . (нужно так же рассмотреть и ).
Теперь и «наоборот», то есть 2.
Пусть оказалось так, что у четырехугольника сумма каких – то двух противоположных углов равна . Скажем, пусть
.

Мы пока не знаем, можем ли описать вокруг него окружность. Но мы точно знаем, что вокруг треугольника мы гарантированно окружность описать можем. Так и сделаем это.
Если точка не «села» на окружность, то она неминуемо оказалась или снаружи или внутри.
Рассмотрим оба случая.
Пусть сначала точка – снаружи. Тогда отрезок пересекает окружность в какой-то точке . Соединим и . Получился вписанный (!) четырехугольник .

Про него уже знаем, что сумма его противоположных углов равна , то есть , а по условию у нас .
Получается, что должно бы быть так, что .
Но это никак не может быть поскольку – внешний угол для и значит, .
А внутри? Проделаем похожие действия. Пусть точка внутри.

Тогда продолжение отрезка пересекает окружность в точке . Снова – вписанный четырехугольник , а по условию должно выполняться , но — внешний угол для и значит, , то есть опять никак не может быть так, что .
То есть точка не может оказаться ни снаружи, ни внутри окружности – значит, она на окружности!
Доказали всю-всю теорему!
Теперь посмотрим, какие же хорошие следствия даёт эта теорема.
Следствие 1
Параллелограмм, вписанный в окружность, может быть только прямоугольником.

Давай-ка поймём, почему так. Пусть параллелограмм вписан в окружность. Тогда должно выполняться .
Но из свойств параллелограмма мы знаем, что .
То есть
И то же самое, естественно, касательно углов и .
Вот и получился прямоугольник – все углы по .

Но, кроме того, есть ещё дополнительный приятный факт: центр окружности, описанной около прямоугольника, совпадает с точкой пересечения диагоналей.
Давай поймём почему. Надеюсь, ты отлично помнишь, что угол, опирающийся на диаметр – прямой.
Ну вот,
— диаметр,
— диаметр
а значит, – центр. Вот и всё.
Следствие 2
Трапеция, вписанная в окружность – равнобедренная.
Докажем?

Пусть трапеция вписана в окружность. Тогда .
Но
То есть
. И так же .

Всё ли мы обсудили? Не совсем. На самом деле есть ещё один, «секретный» способ, как узнавать вписанный четырехугольник. Мы этот способ сформулируем не очень строго (но понятно), а докажем только в последнем уровне теории.
Итак:
Если в четырёхугольнике можно наблюдать такую картинку, как здесь на рисунке (тут углы, «смотрящие» на сторону из точек и , равны), то такой четырехугольник – вписанный.

Это очень важный рисунок – в задачах часто бывает легче найти равные углы, чем сумму углов и .
Несмотря на совершенное отсутствие строгости в нашей формулировке, она верна, и более того, всегда принимается проверяющими ЕГЭ. Ты должен писать примерно так:
« — вписанный» — и всё будет отлично!
Не забывай этот важный признак – запомни картинку, и, возможно, она тебе вовремя бросится в глаза при решении задачки.
Вписанный четырехугольник. Краткое описание и основные формулы
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна
и наоборот:
Если у четырехугольника есть два противоположных угла, сумма которых равна , то такой четырехугольник вписанный.
Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна .
.
Параллелограмм, вписанный в окружность – непременно прямоугольник, и центр окружности совпадает с точкой пересечения диагоналей.

Трапеция, вписанная в окружность – равнобокая.

ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
можно кликнув по этой ссылке.
Определение
Если все вершины четырехугольника принадлежат окружности, то он называется вписанным в эту окружность, а окружность — описанной около него.
Для начала найдем ГМТ, из которых данный отрезок виден под данным углом $alpha$, если $alpha$: 1) прямой; 2) острый; 3) тупой.
Утверждение 1
ГМТ, из которых данный отрезок $AB$ виден под прямым углом, является окружность, построенная на отрезке $AB$ как на диаметре, исключая точки $A$ и $B$.
Построим окружность с диаметром $AB$. Пусть $C$ — произвольная точка окружности, отличная от $A$ и $B$. Тогда $angle ACB = 90^circ$, так как опирается на диаметр. Следовательно, точка $C$ удовлетворяет условию. Осталось доказать, что другие точки условию не удовлетворяют.
Пусть точка $C$ лежит вне окружности. Тогда отрезок $AC$ пересекает окружность. Обозначив точку пересечения через $K$, получим, что $angle AKB = 90^circ$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ острый, то есть точка $C$ условию не удовлетворяет.

Пусть теперь точка $C$ лежит внутри окружности. Обозначив точку пересечения луча $AC$ и окружности через $K$ получим, что $angle AKB = 90^circ$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ тупой, то есть точка $C$ условию не удовлетворяет.
Утверждение 2
ГМТ, из которых данный отрезок $AB$ виден под данным углом $alpha$, является объединение двух симметричных дуг, стягиваемых хордой $AB$, за исключением точек $A$ и $B$.

Пусть $alpha$ — острый. Построим окружность с хордой $AB$ и центром в точке $O$ так, чтобы $angle AOB = 2alpha$. Рассмотрим большую дугу данной окружности и дугу, ей симметричную относительно прямой $AB$. Пусть $C$ — произвольная точка такой дуги, отличная от $A$ и $B$. Тогда $angle ACB = 0{,}5angle AOB=alpha$ по теореме о вписанном угле. Следовательно, точки, принадлежащие объединению дуг, удовлетворяют условию.
Осталось доказать, что другие точки условию не удовлетворяют. Рассуждения аналогичны случаю прямого угла.
Пусть точка $C$ лежит вне данной фигуры. Тогда отрезок $AC$ пересекает окружность. Обозначив точку пересечения через $K$, получим, что $angle AKB=alpha$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ меньше $alpha$, то есть точка $C$ условию не удовлетворяет.
Пусть теперь точка $C$ лежит внутри данной фигуры. Обозначив точку пересечения луча $AC$ и окружности через $K$, получим, что $angle AKB=alpha$. Используя теорему о внешнем угле для треугольника $BKC$, получим, что $angle ACB$ больше $alpha$, то есть точка $C$ условию не удовлетворяет.
Если $alpha$ тупой, то, построив аналогичную окружность так, чтобы $angle AOB = 360^circ-2alpha$ выберем меньшую дугу $AB$. Отразив ее симметрично относительно прямой $AB$, получим искомое ГМТ.
Теорема 1
Для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы сумма его противоположных углов была равна $180^{circ}$.
Поскольку сумма углов выпуклого четырехугольника $ABCD$ равна $360^circ$, достаточно доказать, что $angle B + angle D = 180^circ$ тогда и только тогда, когда он вписанный (см. рисунок).

Если он вписанный, то $angle ABC$ и $angle ADC$ опираются на дуги, дополняющие друг друга до окружности. По следствию из теоремы о вписанном угле, их сумма равна $180^circ$, что и требовалось.
Пусть теперь $angle B + angle D = 180^circ$. Предположим противное, пусть четырехугольник не вписанный, то есть описанная окружность треугольника $ABC$ не проходит через точку $D$. Тогда точка $D$ лежит либо внутри, либо вне окружности. Используя ГМТ, из которых данный отрезок виден под данным углом (утверждение 2), получим, что $angle D$ меньше или, наоборот, больше, чем $180^circ-angle B$. Противоречие, значит, точка $D$ лежит на окружности.
Теорема 2
Выпуклый четырёхугольник $ABCD$ является вписанным тогда и только тогда, когда $angle ABD=angle ACD$.
Если он вписанный, то $angle ABD$ и $angle ACD$ опираются на одну дугу. По следствию из теоремы о вписанном угле, $angle ABD=angle ACD$, что и требовалось.

Пусть в выпуклом четырехугольнике $angle ABD=angle ACD$. Заметим, что из точек $B$ и $C$ отрезок $AD$ виден под одним и тем же углом. Поскольку точки $B$ и $C$ лежат в одной полуплоскости относительно прямой $AD$, то они лежат на одной из дуг полученного в утверждении 2 ГМТ. Действительно, если описать окружность около треугольника $ABD$, то точка $C$ должна на ней лежать. Следовательно, $ABCD$ вписан в окружность, что и требовалось.
Итак, мы разобрались с условиями, при которых четырехугольник вписан в окружность. Поскольку центр окружности равноудален от его вершин, то справедливо следующее
Предложение
Серединные перпендикуляры к сторонам вписанного четырехугольника пересекаются в одной точке, которая и является центром описанной около него окружности.
Также можно сформулировать следующее очевидное
Утверждение
Для того чтобы около четырехугольника можно было описать окружность, необходимо и достаточно, чтобы серединные перпендикуляры к трем его сторонам пересекались в одной точке.
Так как центр описанной около четырехугольника окружности равноудален от его вершин, то он принадлежит серединным перпендикулярaм к его сторонам.
Обратно, если серединные перпендикуляры к трем сторонам четырехугольника пересекаются в одной точке, то эта точка будет равноудалена от всех его вершин и поэтому будет центром описанной около него окружности.
Описанные и вписанные окружности
Наглядная геометрия 9 класс. Опорный конспект 2 Описанные и вписанные окружности
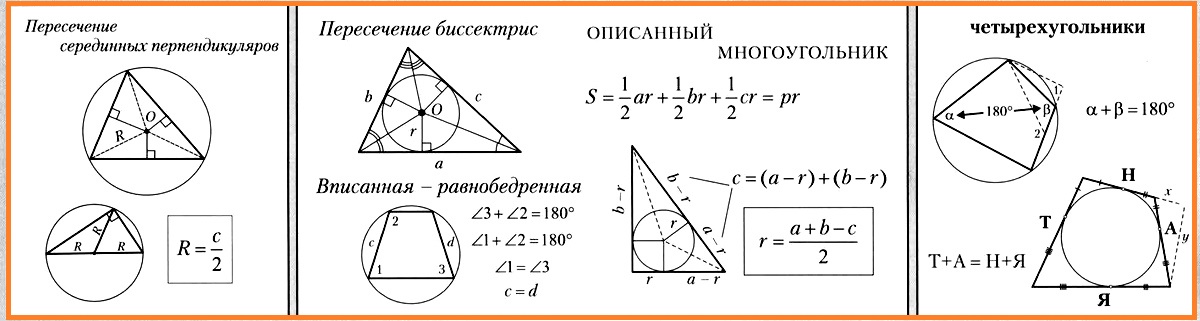
Около любого треугольника можно описать окружность. Она проходит через все вершины треугольника. Вы уже знаете, что точка пересечения серединных перпендикуляров равноудалена от вершин треугольника. Она и является центром описанной окружности.
В любой треугольник можно вписать окружность. Она касается всех сторон треугольника. Вы также знаете, что точка пересечения биссектрис треугольника равноудалена от сторон треугольника. Она и является центром вписанной окружности.
А можно ли описать окружность около любого параллелограмма? Если попробовать это сделать, то окажется, что около параллелограмма можно описать окружность, только если он — прямоугольник. Мы узнаем, каким свойством обладают вписанные и описанные четырехугольники и какие признаки позволяют судить о том, можно ли около данного четырехугольника описать и можно ли в него вписать окружность.
И вдобавок мы познакомимся с одной важной формулой площади треугольника S = рr.
ТАБЛИЦА «Описанные и вписанные окружности»

1. Окружность, описанная около треугольника.
Окружность называется описанной около треугольника, если она проходит через все его вершины.
Теорема. Вокруг любого треугольника можно описать окружность, и только одну. Ее центр лежит на пересечении серединных перпендикуляров к сторонам треугольника.
Доказательство. Точка пересечения серединных перпендикуляров к сторонам треугольника равноудалена от его вершин (доказано нами в 7 классе). Поэтому она является центром описанной окружности, расстояние от этой точки до любой из вершин равно радиусу.
Если существует еще одна описанная окружность, то ее центр равноудален от всех трех вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
2. Окружность, описанная около прямоугольного треугольника.
Теорема. Центр окружности, описанной около прямоугольного треугольника, лежит на середине гипотенузы, а радиус окружности равен половине гипотенузы.
Доказательство. Мы знаем, что медиана прямоугольного треугольника, проведенная из вершины прямого угла, равна половине гипотенузы (доказано нами в 7 классе). Поэтому середина гипотенузы является центром описанной окружности, а ее радиус равен половине гипотенузы, т. е. R = c/2.
3. Окружность, вписанная в треугольник.
Окружность называется вписанной в треугольник, ест она касается всех сторон треугольника.
Теорема. В любой треугольник можно вписать окружность, и только одну. Ее центр лежит на пересечении биссектрис треугольника.
Доказательство. Точка пересечения биссектрис треугольника равноудалена от сторон треугольника (доказано нами в 7 классе). Если из этой точки опустить перпендикуляры на стороны и провести окружность радиусом, равным перпендикуляру, то стороны треугольника будут касаться окружности по признаку касательной.
Если существует еще одна вписанная окружность, то ее центр равноудален от всех трех сторон и поэтому совпадает с точкой пересечения биссектрис, а радиус совпадает с радиусом первой окружности. Окружности совпадают.
4. Формула площади S = рr.
Теорема. Площадь треугольника S = рr, где р — полупериметр треугольника, r — радиус вписанной окружности.
Доказательство. Соединим центр вписанной окружности с вершинами треугольника, стороны которого равны а, b и с. Получим три треугольника, для которых радиусы вписанной окружности, проведенные в точки касания, являются высотами. Площадь данного треугольника равна сумме площадей этих треугольников:![]()
где p — полупериметр треугольника.
Данная формула справедлива для любого многоугольника, в который можно вписать окружность, т. е. для любого описанного многоугольника. Доказательство аналогично.
5. Окружность, вписанная в прямоугольный треугольник.
Теорема. Радиус окружности, вписанной в прямоугольный треугольник, находится по формуле r = (а + b – c)/2.
Доказательство. Проведем радиусы в точки касания. Получим квадрат со стороной r (четырехугольник, у которого все углы прямые и две соседние стороны равны по r) и отрезки катетов, равные r и а – r для катета а, r и b – r для катета b. Так как отрезки касательных, проведенных из одной точки, к окружности равны, то гипотенуза равна сумме отрезков (a – r) и (b – r). Так как с = (а – r) + (b – r), то r = (а + b – c)/2.
6. Свойство вписанного четырехугольника.
Теорема (свойство вписанного четырехугольника). Если четырехугольник вписан в окружность, то суммы его противоположных углов равны по 180°.
Доказательство. Противоположные углы α и β являются вписанными. Они опираются на дуги, которые дополняют друг друга до окружности. Окружность содержит 360°. Так как вписанный угол равен половине дуги, на которую он опирается, то сумма углов α и β равна 180°.
7. Признак вписанного четырехугольника.
Теорема (признак вписанного четырехугольника). Если сумма противоположных углов четырехугольника равна 180°, то вокруг него можно описать окружность.
Доказательство. Через три вершины четырехугольника всегда можно провести окружность (это вершины некоторого треугольника). Если четвертая вершина будет лежать внутри окружности или вне ее, то угол при этой вершине будет больше или меньше угла β, по свойству внешнего угла треугольника, т. е. 1 < β < 2. Тогда сумма противоположных углов этого четырехугольника не будет равна 180°. Поэтому четвертая вершина такого четырехугольника обязана лежать на окружности.
8. Свойство вписанной трапеции.
Теорема. Вписанная трапеция является равнобедренной.
Доказательство. 1-й способ. ∠1 + ∠2 = 180° как внутренние односторонние при параллельных прямых и секущей, ∠3 + ∠2 = 180° по свойству вписанного четырехугольника. Тогда ∠1 = ∠3 и трапеция равнобедренная по признаку равнобедренной трапеции.
2-й способ. Параллельные прямые отсекают равные дуги. Равные дуги стягиваются равными хордами. Поэтому боковые стороны трапеции равны.
9. Свойство описанного четырехугольника.
Теорема (свойство описанного четырехугольника). Если в четырехугольник можно вписать окружность, то суммы его противоположных сторон равны.
Доказательство. Отрезки касательных, проведенных из одной точки к окружности, равны. Обозначим равные отрезки соответственно одной черточкой, двумя, тремя и четырьмя. Убеждаемся, что суммы противоположных сторон равны: Т + А = Н + Я.
10. Признак описанного четырехугольника.
Теорема (признак описанного четырехугольника). Если у четырехугольника суммы противоположных сторон равны, то в него можно вписать окружность.
Доказательство. Пусть окружность касается только трех сторон. Повернув четвертую сторону вокруг вершины так, чтобы она касалась окружности, получим описанный четырехугольник.
Т + А = Н + Я — по свойству описанного четырехугольника,
Т + y = (Н + х) + Я — по условию.
Тогда y = А + х. А это противоречит неравенству треугольника у < А + х. Значит, окружность касается всех четырех сторон заданного четырехугольника.
ЭТО НУЖНО ЗНАТЬ !

Это опорный конспект № 2 по геометрии для 9 класса «Описанные и вписанные окружности». Выберите дальнейшие действия:
- Вернуться к Списку конспектов по геометрии
- Смотреть Опорный конспект 1. Окружности
- Смотреть Опорный конспект 3. Теорема синусов. Теорема косинусов
- Смотреть Опорный конспект 4. Правильные многоугольники
