Каким свойством обладает умножение дробей
Еще одно действие, которое можно выполнять с обыкновенными дробями, – умножение. Мы попробуем разъяснить его основные правила при решении задач, покажем, как умножается обыкновенная дробь на натуральное число и как правильно выполнить умножение трех обыкновенных дробей и больше.
Как умножить одну обыкновенную дробь на другую
Запишем сначала основное правило:
Определение 1
Если мы умножим одну обыкновенную дробь, то числитель дроби, полученной в результате, будет равен произведению числителей исходных дробей, а знаменатель – произведению их знаменателей. В буквенном виде для двух дробей a/b и c/d это можно выразить как ab·cd=a·cb·d.
Посмотрим на примере, как правильно применить это правило. Допустим, у нас есть квадрат, сторона которого равна одной числовой единице. Тогда площадь фигуры составит 1 кв. единицу. Если разделить квадрат на равные прямоугольники со сторонами, равными 14 и 18 числовой единицы, у нас получится, что он теперь состоит из 32 прямоугольников (потому что 8·4=32). Соответственно, площадь каждого из них будет равна 132 от площади всей фигуры, т.е. 132 кв. единицы.
Далее нам надо выделить цветом часть исходного квадрата так, как это сделано на рисунке:
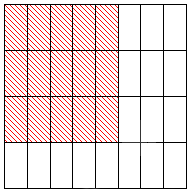
У нас получился закрашенный фрагмент со сторонами, равными 58 числовой единицы и 34 числовой единицы. Соответственно, для вычисления его площади надо умножить первую дробь на вторую. Она будет равна 58·34 кв. единиц. Но мы можем просто подсчитать, сколько прямоугольников входит во фрагмент: их 15, значит, общая площадь составляет 1532 квадратных единиц.
Поскольку 5·3=15 и 8·4=32, мы можем записать следующее равенство:
58·34=5·38·4=1532
Оно является подтверждением сформулированного нами правила умножения обыкновенных дробей, которое выражается как ab·cd=a·cb·d. Оно действует одинаково как для правильных, так и для неправильных дробей; с помощью него можно умножить дроби и с разными, и с одинаковыми знаменателями.
Разберем решения нескольких задач на умножение обыкновенных дробей.
Пример 1
Умножьте 711 на 98.
Решение
Для начала подсчитаем произведение числителей указанных дробей, умножив 7 на 9. У нас получилось 63. Затем вычислим произведение знаменателей и получим: 11·8=88. Составим их двух чисел ответ: 6388.
Все решение можно записать так:
711·98=7·911·8=6388
Ответ: 711·98=6388.
Если в ответе у нас получилась сократимая дробь, нужно довести вычисление до конца и выполнить ее сокращение. Если же у нас получилась неправильная дробь, из нее надо выделить целую часть.
Пример 2
Вычислите произведение дробей 415 и 556.
Решение
Cогласно изученному выше правилу, нам надо умножить числитель на числитель, а знаменатель на знаменатель. Запись решения будет выглядеть так:
415·556=4·5515·6=22090
Мы получили сократимую дробь, т.е. такую, у которой есть признак делимости на 10.
Выполним сокращение дроби: 22090 НОД (220, 90)=10, 22090=220:1090:10=229. В итоге у нас получилась неправильная дробь, из которой мы выделим целую часть и получим смешанное число: 229=249.
Ответ: 415·556=249.
Для удобства вычисления мы можем сократить и исходные дроби перед выполнением действия умножения, для чего нам надо привести дробь к виду a·cb·d. Разложим значения переменных на простые множители и одинаковые из них сократим.
Поясним, как это выглядит, используя данные конкретной задачи.
Пример 3
Вычислите произведение 415·556.
Решение
Запишем вычисления, исходя из правила умножения. У нас получится:
415·556=4·5515·6
Поскольку как 4=2·2, 55=5·11, 15=3·5 и 6=2·3, значит,4·5515·6=2·2·5·113·5·2·3.
Далее мы можем просто сократить некоторые множители и получить следующее: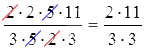 
.
Нам осталось подсчитать несложные произведения в числителе и знаменателе и выделить целую часть из получившейся в итоге неправильной дроби:
2·113·3=229=249
Ответ: 415·556=249.
Числовое выражение, в котором имеет место умножение обыкновенных дробей, обладает переместительным свойством, то есть при необходимости мы можем изменить порядок следования множителей:
ab·cd=cd·ab=a·cb·d
Как перемножить обыкновенную дробь с натуральным числом
Запишем сразу основное правило, а потом попробуем объяснить его на практике.
Определение 2
Чтобы умножить обыкновенную дробь на натуральное число, нужно умножить числитель этой дроби на это число. При этом знаменатель итоговой дроби будет равен знаменателю исходной обыкновенной дроби. Умножение некоторой дроби ab на натуральное число n можно записать в виде формулы ab·n=a·nb.
Понять эту формулу легко, если вспомнить, что любое натуральное число может быть представлено в виде обыкновенной дроби со знаменателем, равным единице, то есть:
ab·n=ab·n1=a·nb·1=a·nb
Поясним нашу мысль конкретными примерами.
Пример 4
Вычислите произведение 227 на 5.
Решение
В результате умножения числителя исходной дроби на второй множитель получим 10. В силу правила, указанного выше, мы получим в результате 1027. Все решение приведено в этой записи:
227·5=2·527=1027
Ответ: 227·5=1027
Когда мы перемножаем натуральное число с обыкновенной дробью, то часто приходится сокращать результат или представлять его как смешанное число.
Пример 5
Условие: вычислите произведение 8 на 512.
Решение
По правилу выше мы умножаем натуральное число на числитель. В итоге получаем, что 512·8=5·812=4012. Итоговая дробь имеет признаки делимости на 2, поэтому нам нужно выполнить ее сокращение:
НОК(40, 12)=4, значит, 4012=40:412:4=103
Теперь нам осталось только выделить целую часть и записать готовый ответ: 103=313.
В этой записи можно видеть все решение целиком: 512·8=5·812=4012=103=313.
Также мы могли сократить дробь с помощью разложения числителя и знаменателя на простые множители, и результат получился бы точно таким же.
Ответ: 512·8=313.
Числовое выражение, в котором натуральное число умножается на дробь, также обладает свойством перемещения, то есть порядок расположения множителей не влияет на результат:
ab·n=n·ab=a·nb
Как выполнить умножение трех и более обыкновенных дробей
Мы можем распространить на действие умножения обыкновенных дробей те же свойства, которые характерны для умножения натуральных чисел. Это следует из самого определения данных понятий.
Благодаря знанию сочетательного и переместительного свойства можно перемножать три обыкновенные дроби и более. Допустимо переставлять множители местами для большего удобства или расставлять скобки так, как будет легче считать.
Покажем на примере, как это делается.
Пример 6
Умножьте четыре обыкновенные дроби 120, 125, 37 и 58.
Решение: для начала сделаем запись произведения. У нас получится 120·125·37·58. Нам надо перемножить между собой все числители и все знаменатели: 120·125·37·58=1·12·3·520·5·7·8.
Перед тем, как начать умножение, мы можем немного облегчить себе задачу и разложить некоторые числа на простые множители для дальнейшего сокращения. Это будет проще, чем сокращать уже готовую дробь, получившуюся в результате.
1·12·3·520·5·7·8=1·(2·2·3)·3·52·2·5·5·7(2·2·2)=3·35·7·2·2·2=9280
Ответ: 1·12·3·520·5·7·8=9280.
Пример 7
Перемножьте 5 чисел 78·12·8·536·10.
Решение
Для удобства мы можем сгруппировать дробь 78 с числом 8, а число 12 с дробью 536, поскольку при этом нам будут очевидны будущие сокращения. В итоге у нас получится:
78·12·8·536·10=78·8·12·536·10=7·88·12·536·10=71·2·2·3·52·2·3·3·10==7·53·10=7·5·103=3503=11623
Ответ: 78·12·8·536·10=11623.
Учебник для 6 класса
Математика
Задача 1. В бутылке 
л сока. Сколько сока в 5 таких бутылках?
Решение. Для решения задачи надо найти произведение • 5. Но умножить на натуральное число 5 — значит найти сумму пяти слагаемых, каждое из которых равно .
Значит, в 5 бутылках 3 л сока.
Чтобы умножить дробь на натуральное число, надо её числитель умножить на это число, а знаменатель оставить без изменения.
Задача 2. Длина прямоугольника 
дм, а ширина 
дм (рис. 19). Чему равна площадь прямоугольника?
Рис. 19
Решение. Из рисунка видно, что данный прямоугольник можно получить так: разделить одну сторону квадрата со стороной 1 дм на 5 одинаковых частей и взять 4 такие части, а другую сторону разделить на 3 одинаковые части и взять 2 такие части. При таком делении квадрат будет состоять из 15 равных частей, а прямоугольник будет состоять из 8 таких частей. Значит, площадь прямоугольника равна 
дм2. Но мы знаем, что площадь прямоугольника равна произведению длины и ширины. Следовательно, число можно получить умножением на .
Итак, 
Чтобы умножить дробь на дробь, надо:
- найти произведение числителей и произведение знаменателей этих дробей;
- первое произведение записать числителем, а второе — знаменателем.
Обычно вначале обозначают произведение числителей и произведение знаменателей, затем производят сокращение и только потом выполняют умножение. В ответе, если это возможно, из дроби исключают целую часть. Например:
Задача 3. Сколько километров проедет велосипедист за 
ч, если будет двигаться со скоростью 
км/ч?
Решение. Так как пройденный путь равен произведению скорости и времени, то для решения задачи надо найти произведение чисел и .
Представим каждое из этих чисел в виде неправильной дроби:
Теперь воспользуемся правилом умножения дробей. Получим:
Таким образом, за ч велосипедист проедет 
км.
Для того чтобы выполнить умножение смешанных чисел, надо их записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.
С помощью умножения дробей решают такие же задачи, как и с помощью умножения натуральных чисел.
Задача 4. За 1 ч автоматическая линия производит 
ц пластмассы. Сколько пластмассы линия производит за ч?
Решение. Такие задачи с натуральными числами или с десятичными дробями мы решали с помощью умножения. Решим и эту задачу умножением:
Итак, за ч производится 
ц пластмассы, т. е. 33 кг.
Тот же ответ можно получить, если выразить данные числа в десятичных дробях: = 0,44, = 0,75, 0,44 • 0,75 = 0,33, но 0,33 ц = 33 кг.
Умножение дробей обладает переместительным и сочетательным свойствами.
Кроме того, для любого значения а:
а • 0 = 0 • а = 0; а • 1 = 1 • а = а.
Например, 
Вопросы для самопроверки
- Расскажите, как умножить дробь на натуральное число.
- Расскажите, как выполнить умножение двух дробей и как выполнить умножение смешанных чисел.
- Какими свойствами обладает действие умножения дробей?
- Запишите свойства нуля и единицы при умножении.
Выполните упражнения
427. Выполните умножение:
428. Сторона квадрата 
м. Найдите периметр квадрата.
429. В одну банку помещается 
кг крупы. Сколько этой крупы вместят две, пять, десять таких же банок?
430. Найдите периметр треугольника ABC, если АВ = 
м, ВС больше АВ в 4 раза, а АС меньше ВС на 
м.
431. Выполните умножение:
432. Станок-автомат изготовляет одну деталь за 
мин. За сколько минут станок изготовит 3 детали, 4 детали, 60 деталей?
Произведение дробей, квадраты и кубы дробей можно прочитать так:
— три восьмых умножить на шестнадцать двадцать первых,
— произведение чисел три восьмых и шестнадцать двадцать первых,
— произведение трёх восьмых и шестнадцати двадцать первых.
— квадрат пяти седьмых,
— пять седьмых в квадрате.
— куб двух пятых,
— две пятых в кубе.
433. Выполните действие:
434. Сторона квадрата 
м. Чему равна площадь квадрата?
435. Найдите объём куба, ребро которого 
м.
436. Масса 1 л керосина составляет 
кг. Какова масса 
керосина?
437. Автомашина движется со скоростью км/мин. Какой путь пройдёт автомашина за 
мин; за 
мин?
438. Найдите значение выражения 
двумя способами: по правилу умножения обыкновенных дробей и по правилу умножения десятичных дробей. Сравните результаты.
439. Найдите произведение 
Проверьте результат, представив эти числа в виде десятичных дробей.
440. Представьте первый множитель в виде обыкновенной дроби и выполните умножение: 
441. Представьте первый множитель в виде десятичной дроби и выполните умножение: 
442. Выполните действия: 
443. Измерения прямоугольного параллелепипеда равны 
и 
. Найдите его объём.
444. Представьте в виде произведения двух дробей число:
445. Найдите значение выражения:
446. Выполните умножение:
447. Найдите по формуле пути s = vt значение s, если:
448. Найдите по формуле объёма прямоугольного параллелепипеда
449. Найдите массу метал л ической детали, объём которой равен 
дм3, если масса 1 дм3 этого металла равна 
кг.
450. Два велосипедиста выехали одновременно из одного и того же пункта и двигались в одном и том же направлении. Скорость первого велосипедиста 
км/ч, а скорость второго в 
раза больше. Какое расстояние будет между ними через ч?
451. Маша и Вера вышли из двух сёл навстречу друг другу. Маша шла со скоростью 3 км/ч, и её скорость была в 
раза меньше скорости Веры. Через 
ч девочки встретились. Найдите расстояние между сёлами.
452. Во дворе заливали каток с помощью двух шлангов. Через первый шланг за 1 ч поступало 
м3 воды, а через второй — м3. Первым шлангом каток заливали 
ч, а вторым — в 
раза дольше. Сколько воды израсходовали на заливку катка?
453. С первого поля, площадь которого 
га, собирали с 1 га по 
ц пшеницы, а со второго поля, площадь которого в 
раза больше площади первого поля, собирали по 
ц пшеницы с 1 га. Сколько всего центнеров пшеницы собрали с этих двух полей?
454. Найдите значение выражения:
455. Вычислите устно:
456. Найдите пропущенные числа:
457. Сумму данных дробей сложите с их разностью. Попробуйте догадаться, как быстрее и проще получить ответ:
458. Представьте дробь 
:
- а) в виде разности двух дробей со знаменателем 3; 18; 21;
- б) в виде суммы двух дробей со знаменателем 3; 9; 12.
459. На координатном луче (рис. 20) отмечены дробь 
и число а. Покажите, где расположены на луче точки 
Рис. 20
460. Кто быстрее? Найдите в таблице последовательно все числа от 1 до 25:
461. Найдите значение выражения:
462. В алфавите племени аоку всего 6 букв — А, К, М, О, Р, У. Все слова в языке этого племени состоят из четырёх букв. Какое наибольшее число слов может быть в языке племени аоку? В скольких из этих слов буквы не повторяются?
463. На складе было т зерна. Сколько зерна стало на складе после того, как привезли 
т, а затем увезли 
т?
464. Сколько килограммов составляют:
- а) 1% центнера;
- б) 7% центнера;
- в) 2,5% центнера?
465. Сколько квадратных метров составляют:
- а) 1% гектара;
- б) 3,5% гектара;
- в) 15% ара;
- г) 0,07% квадратного километра?
466. Запишите, какую часть числа составляют: 1%, 3%, 15%, 25%, 10%, 20%, 50%.
467. Запишите в виде десятичной и в виде обыкновенной дроби: 35 %, 48%, 75%, 110%, 125%.
Образец записи: 5% = 0,05 = 
468. Запишите в виде процентов: 
Образец записи: 
469. Решите задачу:
- Задание рабочие выполнили за три дня. В первый день они сделали
всей работы, во второй день — 
всей работы. Какую часть всей работы они выполнили в третий день? - Поле было засеяно за три дня. В первый день была засеяна
всего поля, во второй день 
g всего поля. Какая часть всего поля была засеяна в третий день?
470. Решите уравнение:
471. Упростите выражение:
- 3,7x + 2,5у + 1,6x + 4,8у;
- 4,5m + 1,9n + 3,3m + 4,3n.
472. Выполните умножение:
473. Найдите значение выражения:
474. Скорость улитки 
м/мин. Какое расстояние проползёт улитка
475. Найдите объём прямоугольного параллелепипеда, измерения которого равны 
476. Масса 1 дм3 стали равна 
кг. Найдите массу стального куба, ребро которого 
дм.
477. Колесо делает 
оборота в минуту. Сколько оборотов оно совершит за 3 мин; за 
мин; за 
мин?
478. Выполните действия:
479. Выразите обыкновенной дробью: 26%, 45%, 80%, 90%.
480. Запишите в виде процентов: 0,23; 0,4; 0,07; 
481. Моторная лодка догоняет плот. Сейчас расстояние между ними 35 км. Скорость плота 2,5 км/ч, а скорость моторной лодки 9,5 км/ч. Какое расстояние будет между ними через t часов, если t = 0,5; 3; 5?
482. Решите уравнение:
- а) 9,5x — (3,2x + 1,8x) + 3,75 = 6,9;
- б) 11,3у — (9,7у — 0,8у) + 7,4 = 17.
483. Выполните действия:
7,72 • 2,25 — 4,06: (0,824 + 1,176) — 12,423.
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:
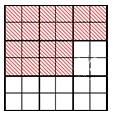
Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.