Каким свойством обладает точка координатной плоскости
Математика – наука довольно сложная. Изучая ее, приходится не только решать примеры и задачи, но и работать с различными фигурами, и даже плоскостями. Одной из наиболее используемых в математике является система координат на плоскости. Правильной работе с ней детей учат не один год. Поэтому важно знать, что это такое и как правильно с ней работать.

Давайте же разберемся, что представляет собой данная система, какие действия можно выполнять с ее помощью, а также узнаем ее основные характеристики и особенности.
Определение понятия
Координатная плоскость — это плоскость, на которой задана определенная система координат. Такая плоскость задается двумя прямыми, пересекающимися под прямым углом. В точке пересечения этих прямых находится начало координат. Каждая точка на координатной плоскости задается парой чисел, которые называют координатами.
В школьном курсе математики школьникам приходится довольно тесно работать с системой координат – строить на ней фигуры и точки, определять, какой плоскости принадлежит та или иная координата, а также определять координаты точки и записывать или называть их. Поэтому поговорим подробнее обо всех особенностях координат. Но прежде коснемся истории создания, а затем уже поговорим о том, как работать на координатной плоскости.
Историческая справка
Идеи о создании системы координат были еще во времена Птоломея. Уже тогда астрономы и математики думали о том, как научиться задавать положение точки на плоскости. К сожалению, в то время еще не было известной нам системы координат, и ученым приходилось пользоваться другими системами.
Изначально они задавали точки с помощью указания широты и долготы. Долгое время это был один из наиболее используемых способов нанесения на карту той или иной информации. Но в 1637 году Рене Декарт создал собственную систему координат, названную впоследствии в честь великого математика «декартовой».

После опубликования труда «Геометрия» система координат Рене Декарта завоевала признание в научных кругах.
Уже в конце XVII в. понятие «координатная плоскость» стало широко использоваться в мире математики. Несмотря на то что с момента создания данной системы прошло уже несколько веков, она до сих пор широко используется в математике и даже в жизни.
Примеры координатной плоскости
Прежде чем говорить о теории, приведем несколько наглядных примеров координатной плоскости, чтобы вы смогли представить ее себе. В первую очередь координатная система используется в шахматах. На доске каждый квадрат имеет свои координаты – одну координату буквенную, вторую – цифровую. С ее помощью можно определить положение той или иной фигуры на доске.
Вторым наиболее ярким примером может служить любимая многими игра «Морской бой». Вспомните, как, играя, вы называете координату, например, В3, таким образом указывая, куда именно целитесь. При этом, расставляя корабли, вы задаете точки на координатной плоскости.
Данная система координат широко применяется не только в математике, логических играх, но и в военном деле, астрономии, физике и многих других науках.
Оси координат
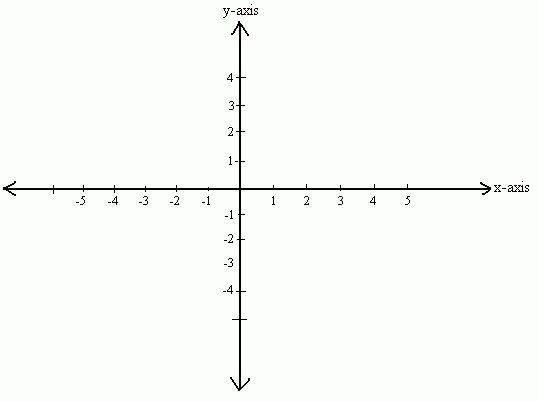
Как уже говорилось, в системе координат выделяют две оси. Поговорим немного о них, так как они имеют немалое значение.
Первая ось — абсцисс — горизонтальная. Она обозначается как (Ox). Вторая ось — ординат, которая проходит вертикально через точку отсчета и обозначается как (Oy). Именно эти две оси образуют систему координат, разбивая плоскость на четыре четверти. Начало отсчета находится в точке пересечения этих двух осей и принимает значение 0. Только в случае если плоскость образована двумя пересекающимися перпендикулярно осями, имеющими точку отсчета, это координатная плоскость.
Также отметим, что каждая из осей имеет свое направление. Обычно при построении системы координат принято указывать направление оси в виде стрелочки. Кроме того, при построении координатной плоскости каждая из осей подписывается.
Четверти
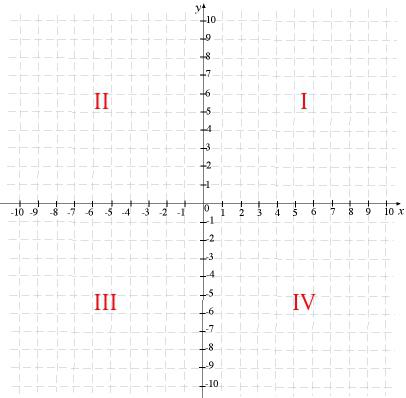
Теперь скажем пару слов о таком понятии, как четверти координатной плоскости. Плоскость разбивается двумя осями на четыре четверти. Каждая из них имеет свой номер, при этом нумерация плоскостей ведется против часовой стрелки.
Каждая из четвертей имеет свои особенности. Так, в первой четверти абсцисса и ордината положительная, во второй четверти абсцисса отрицательная, ордината — положительная, в третьей и абсцисса, и ордината отрицательные, в четвертой же положительной является абсцисса, а отрицательной — ордината.
Запомнив эти особенности, можно с легкостью определить, к какой четверти относится та или иная точка. Кроме того, эта информация может пригодиться вам и в том случае, если придется делать вычисления, используя декартову систему.
Работа с координатной плоскостью
Когда мы разобрались с понятием плоскости и поговорили о ее четвертях, можно перейти к такой проблеме, как работа с данной системой, а также поговорить о том, как наносить на нее точки, координаты фигур. На координатной плоскости сделать это не так тяжело, как может показаться на первый взгляд.
В первую очередь строится сама система, на нее наносятся все важные обозначения. Затем уже идет работа непосредственно с точками или фигурами. При этом даже при построении фигур сначала на плоскость наносятся точки, а затем уже прорисовываются фигуры.
Далее мы поговорим подробнее о построении системы и непосредственно нанесении точек и фигур.
Правила построения плоскости
Если вы решили начать отмечать на бумаге фигуры и точки, вам понадобится координатная плоскость. Координаты точек наносятся именно на нее. Для того чтобы построить координатную плоскость, понадобится только линейка и ручка или карандаш. Сначала рисуется горизонтальная ось абсцисс, затем вертикальная — ординат. При этом важно помнить, что оси пересекаются под прямым углом.
Далее на каждой оси указывают направление и подписывают их с помощью общепринятых обозначений x и y. Также отмечается точка пересечения осей и подписывается цифрой 0.
Следующим обязательным пунктом является нанесение разметки. На каждой из осей в обоих направлениях отмечаются и подписываются единицы-отрезки. Это делается для того, чтобы затем можно было работать с плоскостью с максимальным удобством.
Отмечаем точку
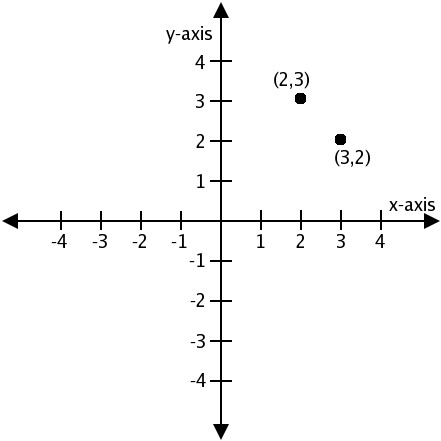
Теперь поговорим о том, как нанести координаты точек на координатной плоскости. Это основа, которую следует знать, чтобы успешно размещать на плоскости разнообразные фигуры, и даже отмечать уравнения.
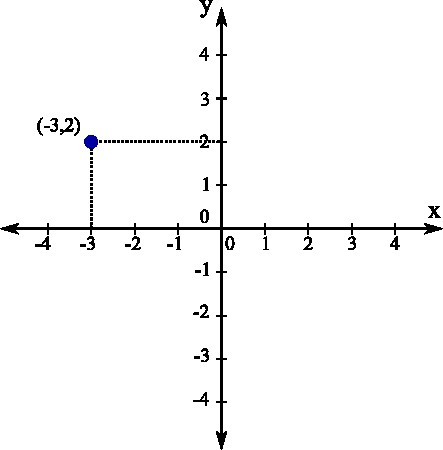
При построении точек следует помнить, как правильно записываются их координаты. Так, обычно задавая точку, в скобках пишут две цифры. Первая цифра обозначает координату точки по оси абсцисс, вторая — по оси ординат.
Строить точку следует таким образом. Сначала отметить на оси Ox заданную точку, затем отметить точку на оси Oy. Далее провести воображаемые линии от данных обозначений и найти место их пересечения — это и будет заданная точка.
Вам останется только отметить ее и подписать. Как видите, все довольно просто и не требует особых навыков.
Размещаем фигуру
Теперь перейдем к такому вопросу, как построение фигур на координатной плоскости. Для того чтобы построить на координатной плоскости любую фигуру, следует знать, как размещать на ней точки. Если вы умеете это делать, то разместить фигуру на плоскости не так уж и сложно.
В первую очередь вам понадобятся координаты точек фигуры. Именно по ним мы и будем наносить на нашу систему координат выбранные вами геометрические фигуры. Рассмотрим нанесение прямоугольника, треугольника и окружности.
Начнем с прямоугольника. Наносить его довольно просто. Сначала на плоскость наносятся четыре точки, обозначающие углы прямоугольника. Затем все точки последовательно соединяются между собой.
Нанесение треугольника ничем не отличается. Единственное – углов у него три, а значит, на плоскость наносятся три точки, обозначающие его вершины.
Касательно окружности тут следует знать координаты двух точек. Первая точка – центр окружности, вторая – точка, обозначающая ее радиус. Эти две точки наносятся на плоскость. Затем берется циркуль, измеряется расстояние между двумя точками. Острие циркуля ставится в точку, обозначающую центр, и описывается круг.
Как видите, тут также нет ничего сложного, главное, чтобы под рукой всегда были линейка и циркуль.
Теперь вы знаете, как наносить координаты фигур. На координатной плоскости это делать не так уж и сложно, как может показаться на первый взгляд.
Выводы
Итак, мы рассмотрели с вами одно из наиболее интересных и базовых для математики понятий, с которым приходится сталкиваться каждому школьнику.
Мы с вами выяснили, что координатная плоскость – это плоскость, образованная пересечением двух осей. С ее помощью можно задавать координаты точек, наносить на нее фигуры. Плоскость разделена на четверти, каждая из которых имеет свои особенности.

Основной навык, который следует выработать при работе с координатной плоскостью, – умение правильно наносить на нее заданные точки. Для этого следует знать правильное расположение осей, особенности четвертей, а также правила, по которым задаются координаты точек.
Надеемся, что изложенная нами информация была доступна и понятна, а также была полезна для вас и помогла лучше разобраться в данной теме.
При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.
Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.
Прямоугольная декартова система координат на плоскости
Чтобы ввести систему координат на плоскости, необходимо провести на плоскости две перпендикулярные прямые. Выбираем положительное направление, обозначая стрелочкой. Необходимо выбрать масштаб. Точку пересечения прямых назовем буквой O. Она считается началом отсчета. Это и называется прямоугольной системой координат на плоскости.
Прямые с началом O, имеющие направление и масштаб, называют координатной прямой или координатной осью.
Прямоугольная система координат обозначается Oxy. Координатными осями называют Ох и Оу, называемые соответственно ось абсцисс и ось ординат.
Изображение прямоугольной системы координат на плоскости.
Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление Ох слева направо, а Oy – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.
Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.
Прямоугольная система координат в трехмерном пространстве
Трехмерное евклидовое пространство имеет аналогичную систему, только оно состоит не из двух, а из трех Ох, Оу, Оz осей. Это три взаимно перпендикулярные прямые, где Оz имеет название ось аппликат.
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.
Оси координат пересекаются в точке O, называемой началом. Каждая ось имеет положительное направление, которое указывается при помощи стрелок на осях. Если при повороте Ох против часовой стрелки на 90° ее положительное направление совпадает с положительным Оу, тогда это применимо для положительного направления Оz. Такую систему считают правой. Иначе говоря, если сравнить направление Х с большим пальцем руки, то указательный отвечает за Y, а средний за Z.
Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.
Координаты точки в декартовой системе координат на плоскости
Для начала отложим точку М на координатной оси Ох. Любое действительное число xM равняется единственной точке М, расположенной на данной прямой. Если точка расположена на координатной прямой на расстоянии 2 от начала отсчета по положительному направлению, то она равна 2 , если -3, то соответственное расстояние 3. Ноль – это начало отсчета координатных прямых.
Иначе говоря, каждая точка М, расположенная на Ox, равна действительному числу xM . Этим действительным числом и является ноль, если точка M расположена в начале координат, то есть на пересечении Ox и Оу. Число длины отрезка всегда положительно, если точка удалена в положительном направлении и наоборот.
Имеющееся число xM называют координатой точки М на заданной координатной прямой.
Возьмем точку как проекцию точки Mx на Ох, а как проекцию точки My на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, где послучим соответственные точки пересечения Mx и My .
Тогда точка Mx на оси Ох имеет соответствующее число xM , а My на Оу — yM. На координатных осях это выглядит так:
Каждая точка M на заданной плоскости в прямоугольной декартовой системе координат имеет одну соответствующую пару чисел (xM, yM), называемую ее координатами. Абсцисса M – это xM , ордината M – это yM .
Обратное утверждение также считается верным: каждая упорядоченная пара (xM, yM) имеет соответствующую заданную в плоскости точку.
Координаты точки в прямоугольной системе координат в трехмерном пространстве
Определение точки М в трехмерном пространстве. Пусть имеются Mx, My, Mz, являющиеся проекциями точки М на соответствующие оси Ох, Оу, Оz. Тогда значения этих точек на осях Ох, Оу, Оz примут значения xM, yM, zM. Изобразим это на координатных прямых.
Чтобы получить проекции точки M, необходимо добавить перпендикулярные прямые Ох, Оу, Оz продолжить и изобразит в виде плоскостей, которые проходят через M. Таким образом, плоскости пересекутся в Mx, My, Mz
Каждая точка трехмерного пространства имеет свои данные (xM, yM, zM) , которые имеют название координаты точки M, , xM, yM, zM- это числа, называемые абсциссой, ординатой и аппликатой заданной точки M. Для данного суждения верно и обратное утверждение: каждая упорядоченная тройка действительных чисел (xM, yM, zM) в заданной прямоугольной системе координат имеет одну соответствующую точку M трехмерного пространства.
Ïðåäñòàâèì íà êîîðäèíàòíîé ïëîñêîñòè ìíîæåñòâî òî÷åê, óäîâëåòâîðÿþùèõ óñëîâèþ õ = 5 è õ = -4,
è ó = -4 è ó = 1.
 ïåðâîì ñëó÷àå ïðÿìûå ïàðàëëåëüíû îñè îðäèíàò, âî âòîðîì – àáñöèññ.
Íà ïðÿìîé ìîæåò áûòü ðàñïîëîæåíî íåîãðàíè÷åííîå êîëè÷åñòâî òî÷åê. È ó âñåãî ýòîãî ìíîæåñòâà òî÷åê, êîîðäèíàòû óäîâëåòâîðÿþò óñëîâèÿì õ = 5 è õ = -4; ó = -4 è ó = 1.
Íà êîîðäèíàòíîé ïðÿìîé íåðàâåíñòâó õ < — 4 ñîîòâåòñòâóåò îòêðûòûé ëó÷, à íà êîîðäèíàòíîé ïëîñêîñòè ýòî æå óñëîâèå îïðåäåëÿåò ïîëóïëîñêîñòü, îíà íàõîäèòñÿ ëåâåå ïðÿìîé õ = -4.
Èçîáðàçèì ìíîæåñòâî òî÷åê, óäîâëåòâîðÿþùèõ óñëîâèþ õ > 3. Ïðîàíàëèçèðóåì, ÷òî ýòî çà òî÷êè:
— ìíîæåñòâî òî÷åê, àáñöèññà êîòîðûõ áîëüøå èëè ðàâíà 3
— òî÷êè, ëåæàùèå ïðàâåå ïðÿìîé õ = 3 è íà ïðÿìîé.
Àëãîðèòì ïîñòðîåíèÿ áóäåò èìåòü âèä:
— ÷èòàåì óñëîâèå: õ > 3;
— ñòðîèì â êîîðäèíàòíîé ïëîñêîñòè ïðÿìóþ: õ = 3;
— îïðåäåëÿåì, ãäå áóäóò íàõîäèòüñÿ òî÷êè, àáñöèññà êîòîðûõ áîëüøå 3; îòâåò – ïðàâåå;
— ìíîæåñòâî âñåõ òî÷åê óäîâëåòâîðÿþùèõ óñëîâèþ õ > 3 ïîêàæåì ïðè ïîìîùè øòðèõîâêè;
õ > 3 çàäàåò ïîëóïëîñêîñòü, íàõîäÿùàÿñÿ ïðàâåå ïðÿìîé õ = 3 è âñå òî÷êè ýòîé ïðÿìîé. Ïðÿìóþ èçîáðàæàåì îäíîé öåëüíîé ëèíèåé, ýòèì óêàçûâàåì, ÷òî âñå òî÷êè ðàñïîëîæåííûå íà ïðÿìîé òàê æå âêëþ÷åíû âî ìíîæåñòâî.
Ïðåäñòàâèì ìíîæåñòâî òî÷åê, óäîâëåòâîðÿþùèõ óñëîâèþ ó < — 2
Àíàëîãè÷íî ïðåäñòàâèì ìíîæåñòâî òî÷åê, óäîâëåòâîðÿþùèõ óñëîâèþ ó > 1.
Ïîñòðîéòå ìíîæåñòâî òî÷åê ó > 1. Ïî àíàëîãèè, òî÷êàì ýòîãî ìíîæåñòâà ïðèñóùå ñâîéñòâî — ó íèõ îðäèíàòà áîëüøå 1.
Ñëåäîâàòåëüíî, îíè áóäóò íàõîäèòüñÿ âûøå ïðÿìîé ó = 1.  ñîîòâåòñòâèè ñî çíàêîì íåðàâåíñòâà òî÷êè ïðÿìîé ó = 1 íå óäîâëåòâîðÿþò óñëîâèþ y > 1. Ãðàôè÷åñêè ìû ýòî ïîêàæåì, èçîáðàçèâ ïðÿìóþ ó = 1 ïóíêòèðîì.
Ïðåäñòàâèì ìíîæåñòâî òî÷åê, ñîîòâåòñòâóþùèõ óñëîâèþ ó > 1 òàê:
Ïðåäñòàâèì íà êîîðäèíàòíîé ïëîñêîñòè ìíîæåñòâà òî÷åê, ñîîòâåòñòâóþùèõ óñëîâèþ: -2 ≤ õ ≤ 2.
Ñõîäíûì îáðàçîì ïðåäñòàâèì ìíîæåñòâî òî÷åê ñîîòâåòñòâóþùèõ óñëîâèþ: 1 < ó < 4.
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó àëãåáðû äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Óðàâíåíèå ëèíèè. | |
| Ëèíèÿ íà ïëîñêîñòè îïðåäåëÿåòñÿ (çàäàåòñÿ) êàê ìíîæåñòâî òî÷åê , õàðàêòåðèçóþùèõñÿ íåêîòîðûì òîëüêî èì ñâîéñòâåííûì ãåîìåòðè÷åñêèì ïðèçíàêîì. | |
| Óðàâíåíèå ëèíèè. | |
