Каким свойством обладает параллелограмм

Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
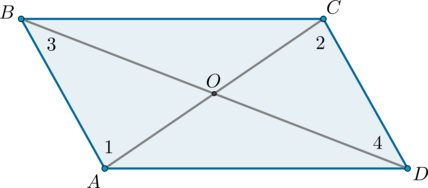
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
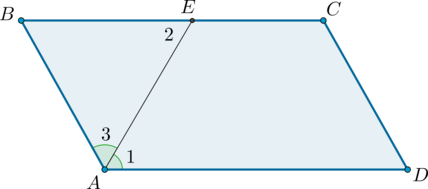
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
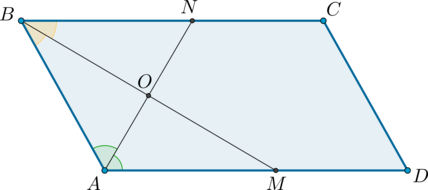
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ — (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).
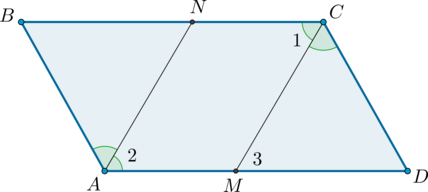
Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).
Ñâîéñòâà ñòîðîí è óãëîâ ïàðàëëåëîãðàììà.
Ó ïàðàëëåëîãðàììà ïðîòèâîïîëîæíûå ñòîðîíû èìåþò îäèíàêîâóþ äëèíó, à ïðîòèâîïîëîæíûå óãëû ðàâíóþ âåëè÷èíó.

Äàíî:
ABCD — ïàðàëëåëîãðàìì.
Äîêàçàòü:
AB=CD, AD=BC,
∠A=∠C, ∠B=∠D.
Äîêàçàòåëüñòâî:
Ïðîâîäèì â ïàðàëëåëîãðàììå ABCD äèàãîíàëü BD.

Ðàññìàòðèâàåì òðåóãîëüíèêè ABD è CDB. Çäåñü âàæíî ïðàâèëüíî óêàçàòü òðåóãîëüíèêè.
1) Ñòîðîíà BD ÿâëÿåòñÿ îáùåé.
2) ∠ABD=∠CDB (êàê âíóòðåííèå íàêðåñò ëåæàùèå ïðè AB∥CD è ñåêóùåé BD)
3) ∠ADB=∠CBD (êàê âíóòðåííèå íàêðåñò ëåæàùèå ïðè AD∥BC è ñåêóùåé BD)
Òî åñòü, ∆ABD= ∆CDB (ïî ñòîðîíå è 2-ì ïðèëåæàùèì ê íåé óãëàì).
Èç ðàâåíñòâà òðåóãîëüíèêîâ ñëåäóåò ðàâåíñòâî ñîîòâåòñòâóþùèõ ñòîðîí:
AB=CD, AD=BC
è ðàâåíñòâî ñîîòâåòñòâóþùèõ óãëîâ:
∠A=∠C.
 ïóíêòàõ 2) è 3) îáúÿñíåíî, ÷òî ∠ABD=∠CDB è ∠ADB=∠CB.
Çíà÷èò,
∠ABC=∠ABD+∠CBD=∠CDB+∠ADB=∠ADC,
Ò.å., ∠B=∠D. ×òî è òðåáîâàëîñü äîêàçàòü.
Ñâîéñòâî óãëîâ ïàðàëëåëîãðàììà, ïðèëåæàùèõ ê îäíîé ñòîðîíå.
Ñóììà óãëîâ ïàðàëëåëîãðàììà, êîòîðûå ïðèëåæàò ê îäíîé ñòîðîíå ñîîòâåòñòâóåò 180 ãðàäóñàì.
Ýòî ñâîéñòâî âûõîäèò èç òîãî, ÷òî óãëû, êîòîðûå ïðèëåæàò ê 1-îé ñòîðîíå ïàðàëëåëîãðàììà îêàçûâàþòñÿ âíóòðåííèìè îäíîñòîðîííèìè óãëàìè ïðè ïàðàëëåëüíûõ ïðÿìûõ.
Äëÿ ïàðàëëåëîãðàììà ABCD:
∠A+∠B=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AD∥BC è ñåêóùåé AB;
∠C+∠D=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AD∥BC è ñåêóùåé CD;
∠A+∠D=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AB∥CD è ñåêóùåé AD;
∠B+∠C=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AB∥CD è ñåêóùåé BC.
Åùå íåêîòîðûå ñâîéñòâà óãëîâ ïàðàëëåëîãðàììà:
Áèññåêòðèñû óãëîâ ïàðàëëåëîãðàììà, êîòîðûå ïðèëåæàò ê îäíîé ñòîðîíå, — ïåðïåíäèêóëÿðíû.
Áèññåêòðèñû ïðîòèâîëåæàùèõ óãëîâ ïàðàëëåëîãðàììà — ïàðàëëåëüíû.
Áèññåêòðèñà óãëà ïàðàëëåëîãðàììà îòñåêàåò îò íåãî ðàâíîáåäðåííûé òðåóãîëüíèê.
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû — ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðàâèëüíàÿ ïèðàìèäà. | |
| Ïðàâèëüíàÿ ïèðàìèäà — êîãäà îñíîâàíèåì ïèðàìèäû ÿâëÿåòñÿ ïðàâèëüíûé ìíîãîóãîëüíèê, à âûñîòà ïðîåöèðóåòñÿ â öåíòð îñíîâàíèÿ (èëè ïðîõîäèò ÷åðåç íåãî). | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðàâèëüíàÿ ïèðàìèäà. | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
| Ïðèçìà ìíîãîãðàííèê, 2 ãðàíè ýòî êîíãðóýíòíûå (ðàâíûå) ìíîãîóãîëüíèêè, êîòîðûå ëåæàò â ïàðàëëåëüíûõ ïëîñêîñòÿõ, à îñòàâøèåñÿ ãðàíè ïàðàëëåëîãðàììû, èìåþùèå îáùèå ñòîðîíû ñ ýòèìè ìíîãîóãîëüíèêàìè. | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
Параллелограмм.
Приступаем к изучению разных видов четырёхугольников.
Определение. Параллелограммом называется выпуклый четырёхугольник, у которого стороны попарно параллельны.

– параллелограмм. У него .
Рассмотрим свойства параллелограмма.
ТЕОРЕМА. У параллелограмма противолежащие стороны и углы равны.

Дано: – параллелограмм
Доказать:
Доказательство.
1. Проведём диагональ . Рассмотрим и .
2. и ; и – внутренние односторонние при параллельных прямых, значит,
.
3. Итак, , ч.т.д.
ТЕОРЕМА. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Дано: – параллелограмм
и – диагонали
Доказать:
Доказательство.
1. Т.к. параллелограмм является выпуклым четырёхугольником, то, по свойству выпуклых многоугольников, его диагонали пересекаются, т.е. .
2. Рассмотрим и .
по II признаку равенства треугольников , ч.т.д.
Итак, параллелограмм обладает двумя свойствами:
Противолежащие стороны и углы параллелограмма равны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Признаки параллелограмма.
Часто бывает ситуация, когда известны какие-то свойства четырёхугольника, а какой вид имеет этот четырёхугольник неизвестно. В этом случае помогут признаки параллелограмма.
ТЕОРЕМА (I признак параллелограмма).
Если в четырёхугольнике две стороны равны и параллельны, то такой четырёхугольник является параллелограммом.

Дано: – четырёхугольник
Доказать: – параллелограмм.
Доказательство.
Проведём диагональ и рассмотрим и .
. Эти углы являются внутренними накрест лежащими при прямых и , значит, по признаку параллельности прямых, .
Итак, в четырёхугольнике , т.е. стороны попарно параллельны, значит, – параллелограмм (по определению), ч.т.д.
ТЕОРЕМА (II признак параллелограмма).
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник является параллелограммом.

Дано: – четырёхугольник
Доказать: – параллелограмм.
Доказательство.
Проведём диагональ и рассмотрим и .
и . А эти пары углов являются внутренними накрест лежащими. По признаку параллельных прямых: «если внутренние накрест лежащие углы равны, то прямые параллельны», делаем вывод, что , а . По определению параллелограмма, данный четырёхугольник является параллелограммом, ч.т.д.
ТЕОРЕМА (III признак параллелограмма).
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник является параллелограммом.

Дано: – четырёхугольник,
и – диагонали, ,
Доказать: – параллелограмм.
Доказательство.
Рассмотрим и .
по I признаку равенства треугольников и . А эти углы являются внутренними накрест лежащими при прямых и , значит, .
Мы доказали, что в четырёхугольнике две стороны параллельны и равны (), значит, по I признаку, этот четырёхугольник является параллелограммом, ч.т.д.
Начертите параллелограмм . Проведите в нём диагонали и . Обозначьте их точку пересечения буквой .
Найдите длину отрезка , если известно, что диагональ см.
Чему равна диагональ , если известно, что отрезок см?
Найдите периметр треугольника , если сторона равна см, а диагонали и равны см и см соответственно.
Две стороны параллелограмма равны см и см. Найдите периметр параллелограмма.
Сумма двух противолежащих углов параллелограмма равна . Чему равны эти углы?
Периметр параллелограмма равен см. Одна из его сторон равна см. Определите остальные стороны параллелограмма.
Найдите углы параллелограмма, если известно, что один из них равен сумме двух других углов параллелограмма.
Одна из сторон параллелограмма равна см, а другая – в раза меньше. Найдите периметр параллелограмма.
Высоты параллелограмма равны см и см. Найдите расстояние от точки пересечения диагоналей параллелограмма до одной из меньших сторон.
В параллелограмме сторона см, диагонали равны см и см, точка – точка пересечения диагоналей. Чему равен периметр треугольника ?
В параллелограмме один угол равен . Найдите остальные углы параллелограмма.
В треугольнике . Из точки, взятой на стороне , проведены две прямые, параллельные сторонам и . Определите вид получившегося четырёхугольника и все его углы.

Четырёхугольник – параллелограмм, отрезки равны. Докажите, что также является параллелограммом.

Диагональ параллелограмма продолжена на равные отрезки и . Докажите, что также является параллелограммом.
В параллелограмме биссектриса угла пересекает сторону в точке , причём, . Найдите периметр параллелограмма.
Диагональ параллелограмма составляет со сторонами параллелограмма углы в и . Найдите углы параллелограмма.
Стороны параллелограмма относятся как , а его периметр равен см. Найдите стороны параллелограмма.
В четырёхугольнике . Диагонали четырёхугольника пересекаются в точке . Найдите периметр .
Из вершины параллелограмма с острым углом проведён перпендикуляр к прямой . Найдите и .
В выпуклом четырёхугольнике . Докажите, что .
Середина отрезка является центром окружности с диаметром , причём, точки не лежат на одной прямой. Докажите, что .
Постройте параллелограмм по большей стороне, меньшей диагонали и углу между ними.
В четырёхугольнике – точка пересечения диагоналей. Периметр треугольника равен см, см, см. Найдите .
Дан параллелограмм с острым углом . Из вершины опущен перпендикуляр к прямой . Найдите и .
В выпуклом шестиугольнике все стороны равны, . Докажите, что .
Дан параллелограмм . На продолжении диагонали за вершины и отмечены точки и соответственно так, что . Докажите, что .
Постройте параллелограмм по меньшей стороне, острому углу и углу между этой стороной и меньшей диагональю.
Одна сторона параллелограмма втрое больше другой стороны. Найдите стороны параллелограмма, если его периметр равен см.
В параллелограмме с острым углом из вершины проведён перпендикуляр к прямой . Найдите углы параллелограмма, если .
Один из углов параллелограмма на меньше другого. Найдите углы параллелограмма.
В параллелограмме с острым углом из вершины проведён перпендикуляр к прямой . Найдите углы параллелограмма, если .
Докажите, что четырёхугольник, имеющий центр симметрии, является параллелограммом.
На диагонали параллелограмма отмечены две точки и так, что . Докажите, что четырёхугольник – параллелограмм.
На сторонах и параллелограмма вне его построены правильные треугольники и . Докажите, что треугольник равносторонний.
Докажите, что выпуклый четырёхугольник является параллелограммом, если .
Угол параллелограмма меньше угла . Докажите, что .
В параллелограмме проведена биссектриса угла , которая пересекает сторону в точке .
Докажите, что треугольник равнобедренный.
Найдите сторону , если см, а периметр параллелограмма равен см.
На стороне параллелограмма взята точка так, что .
Докажите, что – биссектриса угла .
Найдите периметр параллелограмма, если см, см.
В выпуклом четырёхугольнике диагонали и пересекаются в точке . – медиана треугольника , – медиана треугольника . Докажите, что – параллелограмм.
Прямая параллельна стороне параллелограмма и пересекает стороны и в точках и соответственно. Докажите, что – параллелограмм.
В проведена медиана . На её продолжении за точку отложен отрезок , равный . Докажите, что четырёхугольник является параллелограммом.
Стороны и треугольника продолжены на точку так, что . Докажите, что четырёхугольник – параллелограмм.

– параллелограмм, . Найдите .
Одна из сторон параллелограмма на см больше другой. Периметр параллелограмма равен см. Найдите стороны параллелограмма.
В параллелограмме диагональ перпендикулярна стороне и равна ей. Найдите углы параллелограмма.
Периметр параллелограмма равен см. Найдите длины сторон, если известно, что диагональ параллелограмма делит угол на части и .
В параллелограмме из вершины тупого угла проведена высота к стороне так, что . Найдите углы параллелограмма.
Найдите длины высот параллелограмма, если известно, что стороны см и см, а углы относятся как .
Найдите углы параллелограмма, если известно, что один из них в раз меньше суммы всех остальных углов параллелограмма.
В треугольнике проведена медиана и продолжена на свою длину за точку . Найдите периметр четырёхугольника , если периметр треугольника равен см, см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол . Найдите углы параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите периметр параллелограмма, если см, см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол . Найдите углы параллелограмма.
Периметр параллелограмма равен см. Биссектрисы углов и пересекаются на стороне . Найдите длины сторон параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите углы параллелограмма, если известно, что .
Периметр параллелограмма равен см. Биссектриса угла и биссектриса угла делят сторону на три равные части так, что точка лежит между точками и . Найдите длины сторон параллелограмма.
Биссектриса угла параллелограмма пересекает сторону в точке . Найдите углы параллелограмма, если известно, что .
Биссектриса угла параллелограмма пересекает сторону в её середине . Периметр треугольника равен см, а длина отрезка больше стороны на см. Найдите периметр параллелограмма.
6
Свойства параллелограмма
1. Противоположные стороны тождественны.

Доказательство
Первым делом проведем диагональ AC. Получаются два треугольника: ABC и ADC.

Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC Rightarrow angle 1 = angle 2 как лежащие накрест.
AB || CD Rightarrow angle3 = angle 4 как лежащие накрест.
Следовательно, triangle ABC = triangle ADC (по второму признаку: angle 1 = angle 2, angle 3 = angle 4 и AC — общая).
И, значит, triangle ABC = triangle ADC, то AB = CD и AD = BC.
Доказано!
2. Противоположные углы тождественны.

Доказательство
Согласно доказательству свойства 1 мы знаем, что angle 1 = angle 2, angle 3 = angle 4. Таким образом сумма противоположных углов равна: angle 1 + angle 3 = angle 2 + angle 4. Учитывая, что triangle ABC = triangle ADC получаем angle A = angle C, angle B = angle D.
Доказано!
3. Диагонали разделены пополам точкой пересечения.

Доказательство
Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD. Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что triangle AOB = triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов angle 2 и angle 1) и AO = OC (напротив углов angle 3 и angle 4 соответственно).

Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD; AB || CD Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC?

triangle ABC = triangle ADC по свойству 1: AB = CD, AC — общая и angle 1 = angle 2 как накрест лежащие при параллельных AB и CD и секущей AC.
Но если triangle ABC = triangle ADC, то angle 3 = angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (angle 3 и angle 4 — накрест лежащие тоже равны).

Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

AB = CD, AD = BC Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим данный признак. Еще раз проведем диагональ AC.

По свойству 1 triangle ABC = triangle ACD.

Из этого следует, что: angle 1 = angle 2 Rightarrow AD || BC и angle 3 = angle 4 Rightarrow AB || CD, то есть ABCD — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.

angle A = angle C, angle B = angle D Rightarrow ABCD — параллелограмм.
Доказательство

2 alpha + 2 beta = 360^{circ} (поскольку ABCD — четырехугольник, а angle A = angle C, angle B = angle D по условию).
Получается, alpha + beta = 180^{circ}. Но alpha и beta являются внутренними односторонними при секущей AB.
И то, что alpha + beta = 180^{circ} говорит и о том, что AD || BC.
При этом alpha и beta — внутренние односторонние при секущей AD. И это значит AB || CD.
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC; BO = OD Rightarrow параллелограмм.
Доказательство

BO = OD; AO = OC, angle 1 = angle 2 как вертикальные Rightarrow triangle AOB = triangle COD, Rightarrow angle 3 = angle 4, и Rightarrow AB || CD.
Аналогично BO = OD; AO = OC, angle 5 = angle 6 Rightarrow triangle AOD = triangle BOC Rightarrow angle 7 = angle 8, и Rightarrow AD || BC.
Четвертый признак верен.
