Каким свойством обладает объем фигуры

Данный урок посвящён важному математическому понятию – объему тела. Это одна из главных величин, связанная с геометрическими телами, она измеряется числом умещающихся в теле единичных кубов, т. е. кубов с ребром, равным единице длины. В уроке будут названы основные свойства объёма тела. Вы узнаете, что такое «аддитивность», разберётесь в доказательстве важнейшего следствия, которое будет использоваться при доказательстве формул объёма параллельного параллелепипеда и призмы.
Введение
Рис. 1. Примеры, в которых речь заходит об объеме
Сколько воды нужно, чтобы наполнить бассейн? Сколько сока поместится в кружке? И как определить, золотая корона или нет? (См. Рис. 1.)
Все это и многое другое относится к понятию объема.
Всегда при изучении такой темы возникают сложности: все и так понимают, что такое объем, ведь понятие объема появляется еще в начальной школе… Но проблема в том, что тогда всё формулировалось исключительно на интуитивном уровне. Например, объем стакана – это сколько воды в нем поместится или объем комнаты – сколько в ней воздуха.
Теперь мы можем ввести строгое определение и в соответствии с ним вывести заново некоторые уже известные формулы, а заодно доказать неизвестные.
Рассказ про Архимеда и Эврику
Однажды сиракузский царь Гиерон II поручил своему ювелиру изготовить золотую корону. После изготовления сего абсолютно необходимого для царей предмета в голову Гиерону закралась естественная для руководителя мысль: «А не обманул ли меня мой ювелир? Не подмешал ли он в корону значительную часть серебра вместо золота и не прибрал ли ювелир золото к рукам?»
Проверить это было поручено Архимеду. Нужно было выяснить, содержит ли корона серебро вместо золота, не разрушая при этом само ювелирное изделие. Поиски истины были трудны, над составом сплава великий математик трудился долго и безуспешно, пока, наконец, случайно, во время купанья, погруженный в мысли о вычислении объема сложного тела, Архимед погрузил свое тело в воду… и решение задачи было найдено.
Легенда гласит, что Архимед пришел в полный восторг от этого открытия и голый с криком: «Эврика!» побежал из купальни, чтобы проверить свою теорию.
Великий математик пришел к Гиерону II и попросил предоставить ему слиток золота и слиток серебра точно такого же веса, что и корона. Потом он наполнил доверху сосуд и положил в него слиток серебра. Вполне понятно, что каков был объем серебряного слитка, такое количество воды и вытекло.
Затем, вынув слиток, он долил в этот сосуд точное количество вытесненной воды, измеряя этот объем секстарием. Таким образом, Архимед определил, какой вес серебра соответствует какому количеству воды.
Затем, он опустил золотой слиток в сосуд и тем же способом, при помощи секстариев, великий математик выяснил, насколько меньший объем занимает слиток золота по сравнению со слитком серебра аналогичного веса.
После чего, опять наполнив сосуд и опустив в него корону, Архимед определил, что при погружении короны вытекло больше воды, чем при погружении в сосуд золотой массы того же веса.
Заключение Архимеда было следующим. Так как короной вытеснялось большее количество воды, чем золотым слитком, то в золоте, из которого изготовлена корона, содержится примесь серебра.
Что стало с ювелиром, история умалчивает.
Аналогия с понятием площадь
Рис. 2. Площади фигур на плоскости
Понятие объема в пространстве аналогично понятию площади на плоскости. В курсе планиметрии говорилось, что у каждой фигуры на плоскости есть площадь – положительная величина, которая определяет, сколько места занимает данная фигура на плоскости (см. Рис. 2).
Свойства площади
1. Площадь – величина положительная: .
Рис. 3. Равные фигуры
2. Равные фигуры (см. Рис. 3) имеют равные площади: .
Рис. 4. Фигура из нескольких
3. Если фигура состоит из нескольких частей (см. Рис. 4), то ее площадь равна сумме площадей этих частей: .
Рис. 5. Квадрат со стороной 1
4. Площадь квадрата (см. Рис. 5) равна квадрату его стороны: (для квадрата со стороной ).
Аналогичными свойствами обладает и объем.
Понятие объема
Рис. 6. Ящик объемом 1
Объемом фигуры в пространстве называется положительное число, соответствующее количеству места, занимаемое фигурой в пространстве. Иначе говоря, объем – это такая функция, которая ставит в соответствие каждой фигуре некоторое положительное число, и это число показывает, сколько места в пространстве занимает фигура.
Понятно, что число это без выбора единицы измерения ничего не значит. Например, если объем ящика равен , то он большой или маленький (см. Рис. 6)?
Если , то большой (см. Рис. 7), а если , то размером с спичечный коробок (см. Рис. 8).
Так что перед тем как говорить о числе, необходимо задать единицу измерения (, , и т. д.)
Рис. 9. Куб со стороной 1 см
Почему кубические? Потому что мы будем отталкиваться от куба, то есть все фигуры будем представлять через объем куба. Соответственно, если у куба была сторона см (см. Рис. 9), то его объем будет равен одному кубическому сантиметру: .
Рис. 10. Коробка объемом
Тогда дальше мы будем пытаться понять, из скольки кубиков состоит какая-либо заданная фигура. Например, если взять коробку, которую можно заполнить кубиками, каждый из которых имеет объем , ее объем будет равен (см. Рис. 10).
Объем измеряется не только кубическими единицами, а еще и литрами, галлонами, пинтами, баррелями и так далее, но они не являются базовыми.
Можно измерять не только «кубиками», но и другими объектами, например «бочками» или «кружками» и т. д. Просто кубиками (и вообще прямоугольными параллелепипедами) можно приблизить фигуру сколь угодно точно – поэтому чаще используют именно «кубики».
Предположим, что есть фигура, объем которой равен кубическим сантиметрам. Это значит, что фигура состоит из двух кубиков, каждый из которых имеет объем . Причем фигура не обязательно должна иметь вид двух стоящих рядом или друг на друге кубиков, но тем не менее она должна занимать столько же места в пространстве, сколько в сумме занимают два кубика со стороной см. Обозначается это так: .
Система мер
Удобно, когда везде единые системы обозначения. Если, например, один магазин продает воду литрами, другой – кубическими сантиметрами, третий – пинтами ( пинта литра), то как сравнить, где выгоднее? Можно все свести к одной единице измерения, но это довольно долго и неудобно. С другой стороны, не все удобно измерять в тех же литрах: скажем, нефть обычно измеряют в баррелях, так как, во-первых, получается меньшее число ( баррель литров). Тем не менее, люди стараются одни и те же вещи измерять одинаково: напитки – литрами, материалы (песок, цемент) – кубометрами, нефть – баррелями и т. д. Очень многое зависит и от страны проживания. Так, например, в Британии объем жидкостей чаще измеряется пинтами, у нас – литрами.
Приближенное вычисление площади
Рис. 11. Площадь
Как разбить фигуру на кубики? На самом деле, в качестве аналогии можно вспомнить, как площадь подграфика функции заполняется прямоугольниками (См. Рис. 11).
Рис. 12. Заполнение фигур пространства маленькими
Так мы задавали определенный интеграл. Аналогично заполняются и фигуры в пространстве (см. Рис. 12). Так мы приблизим объем данной фигуры к сумме объемов маленьких кубиков.
Буква V в геометрии
Вы уже привыкли, что объем обозначается буквой , но почему именно это буква? Площадь обозначают от слова Square (площадь). А объем?
Буква в данном случае значит Volume, то есть с латинского – «объем», «наполнение».
Свойства объема
Рис. 13. Равные фигуры
1. Равные фигуры (см. Рис. 13) имеют равные объемы: .
Рис. 14. Пакет молока и кубик одинакового объема
Обратное неверно. Объем может быть одинаков и при разной форме. Например, литровый пакет молока имеет тот же объем, что и кубик со стороной дм (, но фигуры не равны (равными называют, как и на плоскости, те фигуры, которые совмещаются при наложении) (см. Рис. 14).
Рис. 15. Фигура из 3 кубиков
2. Если некоторое тело в пространстве составлено из нескольких тел (без наложений) (см. Рис. 15), то объем исходного тела равен сумме объемов тех тел, из которых оно составлено: .
Сформулированные два свойства обычно называют основными свойствами объемов.
Кроме этого иногда выделяют отдельно третье свойство.
3. Объем единичного куба равен единице: .
Рис. 16. Единичный куб
Эти три свойства нами не доказаны – и доказаны не будут: как и в случае с площадями, они сформулированы как аксиомы объема, а затем уже на их базе будем абсолютно строго выводить различные формулы.
Следствия из третьего свойства
Рис. 17. Куб со стороной
Следствие 1. Объем куба со стороной (см. Рис. 17) равен : .
Доказательство. Пусть , (см. Рис. 18).
Рис. 18. Сторона куба равна
Разобьем куб на маленькие кубики со стороной 1. Раз , то каждая сторона разобьется на частей (см. Рис. 19).
Рис. 19. Разбиение куба на маленькие
Найдем количество кубиков. Очевидно, что слоев будет (см. Рис. 20).
Рис. 20. Разбиение куба на слоев
В каждом слое помещается кубиков. Значит, всего кубиков будет . Объем каждого из них равен 1 (по третьему свойству). Тогда объем всего куба равен (по второму свойству). Имеем, . Что и требовалось доказать.
Следствие 2. Объем куба со стороной () равен :
Рис. 21. Единичный куб
Доказательство. Пусть . Рассмотрим единичный куб (см. Рис. 21).
Рис. 22. Разбиение единичного куба плоскостями
Разобьем его плоскостями (как в следствии 1), а каждую сторону на частей. Соответственно, если сторона равна 1, то каждый образовавшийся отрезок равен (см. Рис. 22).
Количество кубиков, которые помещаются в куб, будет равно . Но объем каждого из них неизвестен, а известен лишь объем большого куба (по третьему свойству). Учитывая то, что единичный куб состоит из маленьких одинаковых кубиков, чьи объемы равны (по первому свойству), то общий объем равен . Тогда . Что и требовалось доказать.
Следствие 3. Объем куба равен кубу его стороны: .
Объем единичного куба. Доказательство Следствия 3
Разберем 3 случая.
— Если сторона куба – натуральное число (, ). Тогда мы получаем следствие 1, которое уже было доказано ранее.
Рис. 23. Разбиение куба на частей
— Если сторона куба – дробное число. Пусть ; . Разобьем каждую сторону на частей. Получаем кубиков, сторона каждого из которых равна (см. Рис. 23).
А тогда объем каждого маленького кубика (по следствию 2). Тогда искомый объем . Что и требовалось доказать.
— Если сторона куба – произвольное вещественное число. Рассмотрим 2 последовательности, они будут строиться следующим образом. Сначала возьмем два соседних целых числа, между которыми заключено число (сторона куба): , . Теперь оценим с точностью до десятых , где . Теперь оценим до сотых , где и т. д.
Соответственно, объем куба со стороной будет больше, чем объем куба со стороной , и меньше, чем объем куба со стороной : , где (; ; ; ; ; и т. д). Если устремить к бесконечности, то мы получим, что левая и правая часть неравенства сколь угодно близки, то есть и стремятся к одному и тому же числу. Таким образом, если перейти к пределу, то получим, что , то есть . Что и требовалось доказать.
Заключение
На этом уроке было введено понятие объема, выяснено, какими свойствами обладает объем, и сформулировано важное следствие . В дальнейшем из полученных свойств и следствий мы выведем формулы объемов для основных фигур в пространстве.
Список литературы
- Геометрия. Учебник для 10–11 классов. Атанасян Л.С. и др. 18-е изд. – М.: Просвещение, 2009. – 255 с.
- А.В. Погорелов. Геометрия 11 класс. – М.: Просвещение, 2002.
- В.Ф. Бутузов, Ю.А. Глазков. Рабочая тетрадь по геометрии 11 класс.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Uztest.ru (Источник).
- School-collection.edu.ru (Источник).
- Yaklass.ru (Источник).
Рекомендованное домашнее задание
- Сколько литров воды вмещает бак, имеющий форму куба с ребром дм?
- Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?
- Площадь поверхности куба равна . Найдите его объем.
ВОПРОСЫ
1. Какими свойствами обладает объем фигуры?
1) Равные фигуры имеют равные объемы.
2) Объем фигуры равен сумме объемов фигур, из которых она состоит.
2. Какой куб называют единичным?
Единичный куб — это куб, ребро которого равно единице измерения отрезков.
3. Приведите примеры единиц измерения объема.

4. Что означает измерить объем фигуры?
Измерить объем фигуры — значит подсчитать, сколько единичных кубов в ней помещается.
5. Чему равен объем прямоугольного параллелепипеда с измерениями а, b, c?

6. По какой формуле вычисляется объем куба?

7. Как вычислить объем прямоугольного параллелепипеда, зная его площадь основания и высоту?

РЕШАЕМ УСТНО
1. Заполните пропуски в цепочки вычислений:

2. Сколько необходимо использовать кубиков с ребром 1 см, сложить кубик с ребром 2 см?
Нужно взять 8 кубиков с ребром 1 см.
3. Сколько сантиметров проволоки необходимо для изготовления проволочного каркаса прямоугольного параллелепипеда, измерения которого равны 3 см, 5 см и 6 см?

4. Расставьте вместо звездочек знаки «+» и » — » так, чтобы запись 20 * 30 * 10 * 80 * 70 = 50 стала верным равенством.
20+30-10+80-70=50.
УПРАЖНЕНИЯ
617. 1) Сколько сантиметров в одном дециметре? Квадратных сантиметров в одном квадратном дециметре? Кубических сантиметров в одном кубическом дециметре?
2) Сколько сантиметров в одном метре? Квадратных сантиметров в одном квадратном метре? Кубических сантиметров в одном кубическом метре?

618. Фигуры, изображенные на рисунке 179, сложены из кубиков, ребра которых равны 1 см. Найдите объем каждой фигуры.

619. Вычислите объем прямоугольного параллелепипеда, измерения которого равны 12 м, 15 м и 6 м.

620. Чему равен объем куба, ребро которого равно 6 см?

621. Чему равен объем прямоугольного параллелепипеда с измерениями 10 дм, 8 дм и 4 дм?

622. Выразите:
1) в кубических миллиметрах: 7 см3, 38 см3; 12 см3 243 мм3; 42 см3 68 мм3; 54 см3 4 мм3; 1 дм3 20 мм3; 18 дм3 172 см3; 35 дм3 67 см3 96 мм3;
2) в кубических дециметрах: 4 м3; 264 м3; 10 м3 857 дм3; 28 м3 2 дм3; 44 000 см3; 5 430 000 см3.


623. Выразите в кубических сантиметрах: 8 дм3; 62 дм3; 378 000 мм3; 520 000 мм3; 78 дм3 325 см3; 56 дм3 14 см3; 8 м3 4 дм3 6 см3.

624. Ширина прямоугольного параллелепипеда равна 15 дм, длина — на 3 дм больше ширины, а высота в 3 раза меньше длины. Найдите объем данного параллелепипеда.

625. Высота прямоугольного параллелепипеда равна 20 см, что на 4 см меньше его длины и в 5 раз больше его ширины. Вычислите объем данного параллелепипеда.

626. Объем прямоугольного параллелепипеда равен 560 см3, длина — 14 см, ширина — 8 см. Найдите высоту данного параллелепипеда.

627. Длина прямоугольного параллелепипеда равна 18 см, высота — 15 см, а объем — 3 240 см3. Найдите ширину данного параллелепипеда.

628. Объем комнаты, имеющей форму прямоугольного параллелепипеда, равен 144 м3, а высота — 4 м. Найдите площадь пола комнаты.

629. Спортивный зал имеет форму прямоугольного параллелепипеда, его объем равен 960 м3, а площадь пола равна 192 м2. Найдите высоту спортивного зала.

630. Найдите объем фигуры, изображенной на рисунке 180 (размеры даны в сантиметрах).

631. Найдите объем фигуры, изображенной на рисунке 181 (размеры даны в сантиметрах).


632. Ребро куба, изготовленного из цинка, равно 4 см. Найдите массу куба, если 1 см3 цинка составляет 7 г.

633. Знайка сконструировал землеройную машину, которая за 8 ч может вырыть траншею, имеющую форму прямоугольного параллелепипеда, длиной 150 м, глубиной 80 см и шириной 60 см. Сколько кубометров земли выкапывает эта машина за 1 ч? Работу скольких коротышек выполняет эта машина, если за 8 ч один коротышка может выкопать 240 дм3 земли?

634. Куб и прямоугольный параллелепипед имеют равные объемы. Найдите площади поверхности куба, если длина прямоугольного параллелепипеда равна 12 см, что в 2 раза больше ширины и в 4 раза больше высоты параллелепипеда.

635. Ребро одного куба в 4 раза больше ребра второго. Во сколько раз: 1) площадь поверхности первого куба больше площади поверхности второго; 2) объем первого куба больше объема второго?

636. Как изменится объем прямоугольного параллелепипеда, если: 1) длину увеличить в 4 раза, ширину — в 2 раза, высоту в 5 раз; 2) ширину уменьшить в 4 раза, высоту в 2 раза, а длину увеличить в 16 раз?

637. Как изменится объем прямоугольного параллелепипеда, если: 1) каждое измерение увеличить в 2 раза; 2) длину уменьшить в 3 раза, высоту — в 5 раз, а ширину увеличить в 15 раз?

638. В бассейн, площадь которого равна 1 га, налили 1 000 000 л воды. Можно ли в этом бассейне провести соревнования по плаванию?

639. В кубе с ребром 3 см проделали три сквозных квадратных отверстия со стороной 1 см (рис. 182). Найдите объем оставшейся части.

640. Размеры куска мыла, имеющего форму прямоугольного параллелепипеда, равны 12 см, 6 см и 4 см. Каждый день используют одинаковую массу мыла. Через 14 дней все размеры куска мыла уменьшились в 2 раза. На сколько дней хватит оставшегося куска мыла?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
641. В школьном коридоре, длина которого равна 30 м, ширина — 35 дм, надо заменить линолеум. Какое наименьшее количество рулонов линолеума для этого нужно, если длина рулона линолеума равна 12 м, а ширина — 160 см?

642. Из двух населенных пунктов, расстояние между которыми равно 54 км, одновременно выехали навстречу друг другу и встретились через 2 ч после начала движения. Скорость движения первого велосипедиста составляла 12 км/ч. С какой скоростью двигался второй велосипедист?

643. Найдите значение выражения:


ЗАДАЧА ОТ МУДРОЙ СОВЫ
644. В записи первого трехзначного числа используются только цифры 2 и 3, а в записи второго — только цифры 3 и 4. Может ли произведение этих чисел записываться только цифрами 2 и 4?
![]()
Статьи
Среднее общее образование
Геометрия
Математика
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
01 апреля 2019
Раньше для определения объемов геометрических тел традиционно использовались интегралы. Сегодня есть и другие подходы, которые подробно представлены в учебниках нашей корпорации. В одном из вебинаров «Российского учебника» учитель высшей категории Алексей Доронин рассказал о методах определения объема разных геометрических тел с помощью принципа Кавальери и других аксиом.
Определение объема
Объем можно определить как функцию V на множестве многогранников, удовлетворяющую следующим аксиомам:
- V сохраняется при движениях.
- V удовлетворяет принципу Кавальери.
- Если внутренности многогранников M и N не пересекаются, то V(M ∪ N) = V(M) + V(N).
- Объем прямоугольного параллелепипеда V = abc.
Принцип Кавальери (итальянского математика, ученика Галилея). Если при пересечении двух тел плоскостями, параллельными одной и той же плоскости, в сечениях этих тел любой из плоскостей получаются фигуры, площади которых относятся как m : n, то объемы данных тел относятся как m : n.
В открытом банке заданий ЕГЭ есть много задач для отработки этого способа определения объема.
Примеры
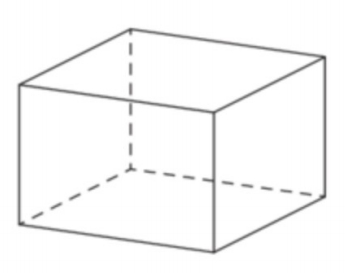
Задача 1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
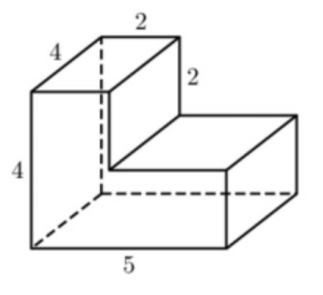
Задача 2. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
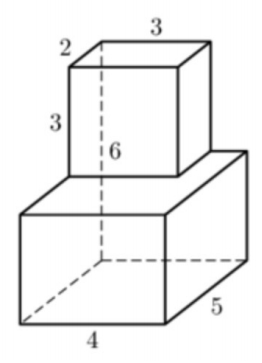
Задача 3. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).
Разберем, как можно вычислять объемы изучаемых в школе фигур.
Объем призмы
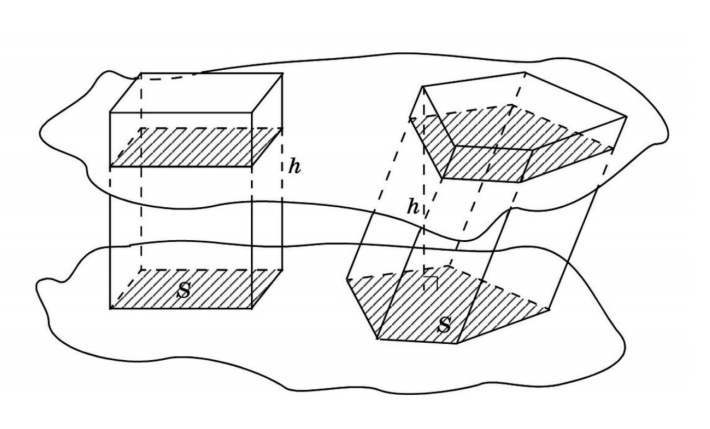
В представленном случае известны площадь основания и высота призмы. Чтобы найти объем, используем принцип Кавальери. Рядом с призмой (Ф2) поместим прямоугольный параллелепипед (Ф1), в основании которого — прямоугольник с такой же площадью, как у основания призмы. Высота у параллелепипеда такая же, как у наклонного ребра призмы. Обозначим третью плоскость (α) и рассмотрим сечение. В сечении виден прямоугольник с площадью S и, во втором случае, многоугольник тоже с площадью S. Далее вычисляем по формуле:
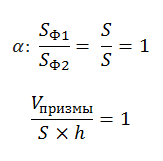
V Sосн h

Математика. Геометрия. Углублённый уровень. 11 класс. Задачник.
Задачник является Частью УМК для 10-11 классов, предназначенного для изучения предмета на углубленном уровне, и содержит более 1000 задач разной степени трудности, помогающих изучению и усвоению материала, изложенного в учебнике.
Пособие соответствует Федеральному государственному образовательному стандарту среднего (полного) общего образования.
Купить
Объем пирамиды
Лемма: две треугольные пирамиды с равновеликими основаниями и равными высотами равновелики. Докажем это, используя принцип Кавальери.
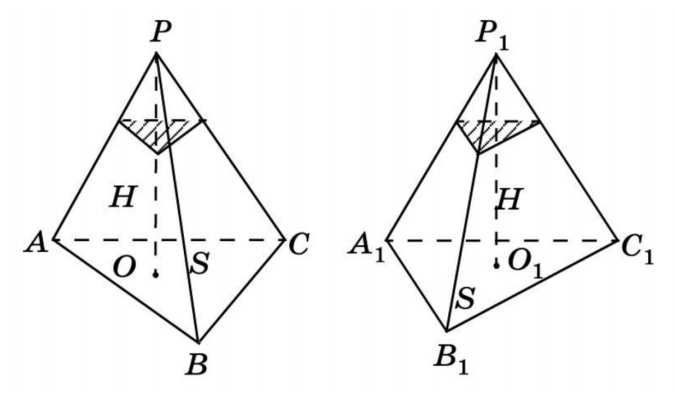
Возьмем две пирамиды одинаковой высоты и заключим их между двумя параллельными плоскостями α и β. Обозначим также секущую плоскость и треугольники в сечениях. Заметим, что отношения площадей этих треугольников связаны непосредственно с отношением оснований.

V 1/V2 = 1 <=> V1 = V2
Известно, что объем любой пирамиды равен одной трети произведения площади основания на высоту. Данной теоремой апеллируют довольно часто. Однако откуда в формуле объема пирамиды появляется коэффициент 1/3? Чтобы понять это, возьмем призму и разобьем ее на 3 треугольные пирамиды:
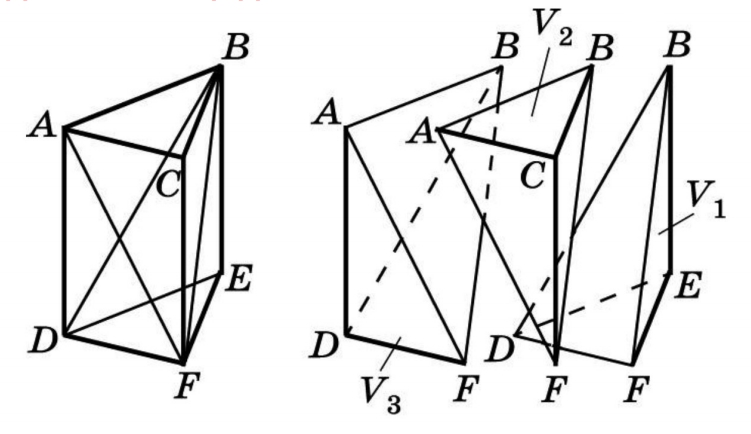
V1 = V2
V2 = V3
Vпризмы S h = 3V
V = 1/3 Sh
Объем цилиндра
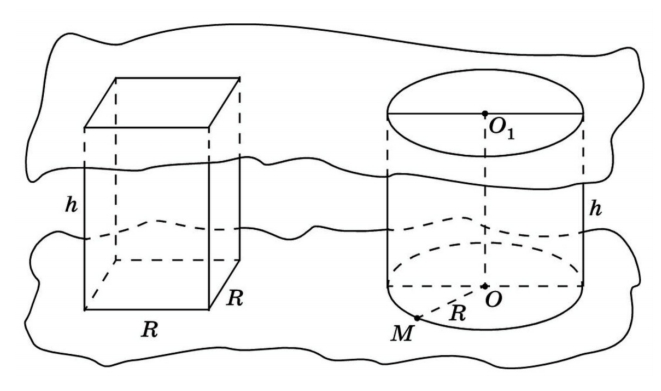
Возьмем прямой круговой цилиндр, в котором известны радиус основания и высота. Рядом поместим прямоугольный параллелепипед, в основании которого лежит квадрат. Рассмотрим:

Vцил = πh × R2
Объем конуса
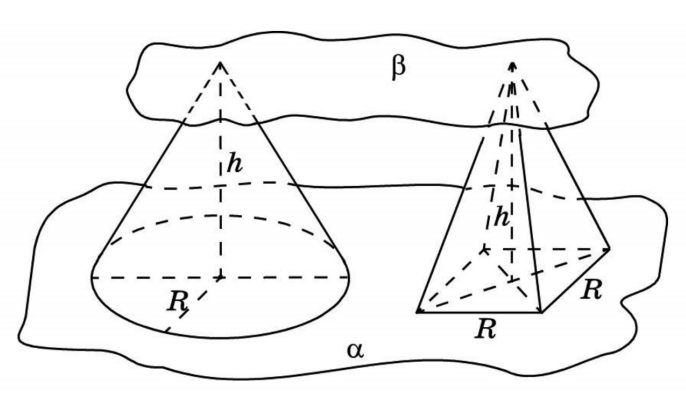
Конус лучше всего сравнивать с пирамидой. Например, с правильной четырехугольной пирамидой с квадратом в основании. Две фигуры с равными высотами заключаем в две параллельные плоскости. Обозначив третью плоскость, в сечении получаем круг и квадрат. Представления о подобиях приводят к числу π.
SФ1/SФ2 = π

Vконуса = 1/3 πR2 h
Объем шара
Объем шара — одна из наиболее сложных тем. Если предыдущие фигуры можно продуктивно разобрать за один урок, то шар лучше отложить на последующее занятие.
Чтобы найти объем шара, шар часто предлагается сравнить со сложным геометрическим телом, которое связано с конусом и цилиндром. Но не стоит строить цилиндр, из которого вырезан конус, или вроде того. Возьмем половину шара с высотой R и радиусом R, а также конус и цилиндр с аналогичными высотами и радиусами оснований. Обратимся к полезным материалам на сайте
«Математические этюды», где объем шара рассматривается с использованием весов Архимеда. Цилиндр располагается на одной стороне уравновешенных весов, конус и половина шара — на другой.
Заключаем геометрические фигуры в две параллельные плоскости и смотрим, что получается в сечении. У цилиндра — круг с площадью πR2. Как известно, если внутренности геометрических тел не пересекаются, то объем их объединения равен сумме объемов. Пусть в конусе и в половине шара расстояние до плоскости сечения будет x. Радиус — тоже x. Тогда площадь сечения конуса — π ∙ x2. Расстояние от середины верха половины шара к краю сечения — R. Площадь сечения половины шара: π(R2 — x2).
Заметим, что: πR2 + πR2 — πR2 = πR2
Vцил = πR2 × R = πR3 = 1/3 R3 π + Vшара
Vшара = 4/3 πR3
Итак, чтобы найти объем нового, не изученного геометрического тела, нужно сравнить его с тем телом, которое наиболее на него похоже. Многочисленные примеры заданий из открытого банка задач показывают, что в работе с ?
