Какие свойства сложения векторов вы знаете
Предварительные сведения
Перед тем как вводить свойства векторов, введем, непосредственно, понятие вектора, а также понятия их сложения, умножения на число и их равенства.
Для того, чтобы ввести определение геометрического вектора вспомним, что такое отрезок. Введем следующее определение.
Определение 1
Отрезком будем называть часть прямой, которая имеет две границы в виде точек.
Отрезок может иметь 2 направления. Для обозначения направления будем называть одну из границ отрезка его началом, а другую границу — его концом. Направление указывается от его начала к концу отрезка.
Определение 2
Вектором или направленным отрезком будем называть такой отрезок, для которого известно, какая из границ отрезка считается началом, а какая его концом.
Обозначение: Двумя буквами: $overline{AB}$ — (где $A$ его начало, а $B$ – его конец).
Одной маленькой буквой: $overline{a}$ (рис. 1).
Введем еще несколько понятий, связанных с понятием вектора.
Чтобы ввести определение равенства двух векторов, сначала нужно разобраться с такими понятиями, как коллинеарность, сонаправленность, противоположная направленность двух векторов, а также длину вектора.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Определение 3
Два ненулевых вектора будем называть коллинеарными, если они лежат на одной и той же прямой или на прямых, параллельных друг другу (рис.2).
Определение 4
Два ненулевых вектора будем называть сонаправленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они будут направлены в одну сторону (рис. 3).
Обозначение: $overline{a}↑↑overline{b}$
Определение 5
Два ненулевых вектора будем называть противоположно направленными, если они удовлетворяют двум условиям:
- Эти векторы коллинеарны.
- Если они направлены в разные стороны (рис. 4).
Обозначение: $overline{a}↑↓overline{d}$
Определение 6
Длиной вектора $overline{a}$ будем называть длину отрезка $a$.
Обозначение: $|overline{a}|$
Перейдем к определению равенства двух векторов
Определение 7
Два вектора будем называть равными, если они удовлетворяют двух условиям:
- Они сонаправлены;
- Их длины равны (рис. 5).
Осталось ввести понятие сложения векторов, а также их умножения на число.
Определение 8
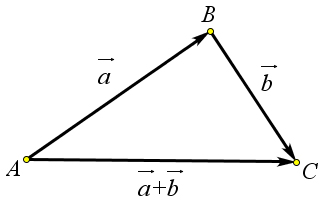
Суммой векторов $overline{a+b}$ будем называть вектор $overline{c}=overline{AC}$, который построен следующим образом: От произвольной точки A отложем $overline{AB}=overline{a}$, далее от точки $B$ отложем $overline{BC}=overline{b}$ и соединим точку $A$ c точкой $C$ (рис. 6).
Определение 9
Произведением вектора $overline{a}$ на $k∈R$ будем называть вектор $overline{b}$ который будет удовлетворять условиям:
- $|overline{b}|=|k||overline{a}|$;
- $overline{a}↑↑overline{b}$ при $k≥0$ и, $overline{a}↑↓overline{b}$ при $k
Свойства сложения векторов
Введем свойства сложения для трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$:
Коммутативность сложения векторов:
$overline{α}+overline{β}=overline{β}+overline{α}$
Ассоциативность трех векторов по сложению:
$(overline{α}+overline{β})+overline{γ}=overline{α}+(overline{β}+overline{γ})$
Сложение с нулевым вектором:
$overline{α}+overline{0}=overline{α}$
Сложение противоположных векторов
$overline{α}+(overline{-α})=overline{0}$
Все эти свойства можно легко проверить с помощью построений таких векторов с помощью определения 8. В двух первых сравнением построенных векторов с правой и левой частей равенства, а в третьем и четвертом с помощью построения вектора с левой стороны.
Свойства умножения вектора на число
Введем свойства умножения для двух векторов $overline{α}$, $overline{β}$ и чисел $a$ и $b$.
- $a(overline{α}+overline{β})=aoverline{α}+aoverline{β}$
- $overline{α}(a+b)=overline{α}a+overline{α}b$
- $(ab)overline{α}=a(boverline{α})=b(aoverline{α})$
- $1cdot overline{α}=overline{α}$
Все эти свойства можно легко проверить с использованием определений 8 и 9. В двух первых сравнением построенных векторов с правой и левой частей равенства, в третьем сравнением всех векторов, входящих в равенство, и в четвертом с помощью построения вектора с левой стороны.
Пример задачи
Пример 1
Провести сложение векторов
$2overline{AB}+(2overline{BC}+3overline{AC})$
Решение.
Используя свойство сложения 2, получим:
$2overline{AB}+(2overline{BC}+3overline{AC})=(2overline{AB}+2overline{BC})+3overline{AC}$
Используя свойство умножения на число 1, получим:
$(2overline{AB}+2overline{BC})+3overline{AC}=2(overline{AB}+overline{BC})+3overline{AC}=2overline{BC}+3overline{AC}=5overline{AC}$
Ответ: $5overline{AC}$.
Основные понятия векторной алгебры
ОСНОВНЫЕ ПОНЯТИЯ ВЕКТОРНОЙ АЛГЕБРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ И ИХ СВОЙСТВА. ЛИНЕЙНО ЗАВИСИМЫЕ (НЕЗАВИСИМЫЕ) СИСТЕМЫ ВЕКТОРОВ. БАЗИС. КООРДИНАТЫ ВЕКТОРА.
Физические величины можно разделить на два вида: скалярные и векторные. Скалярные величины характеризуется числом при данной единице измерения. Такими величинами, например, являются масса, температура, площадь, плотность и т.д.
Def. Величины, которые характеризуются неотрицательным числом при данной единице измерения (модулем) и направлением, называются векторными.
Векторные величины обычно изображают направленными отрезками.
Рассмотрим в пространстве две точки А и В. Они определяют отрезок АВ.
Def. Отрезок АВ называется направленным, если его концы А и В упорядочены; если при этом первой является точка А, а второй – точка В, то А – начало отрезка, а В – его конец.
Направленный отрезок обозначается .
Def.Модулем направленного отрезка называется длина отрезка АВ.
отрезки и содержащие точки и соответственно, расстояние не превосходит некоторого данного расстояния (рис. 10.2).
Def. Если начало и конец направленного отрезка совпадают, то его называют нулевым направленным отрезком. Его модуль считается равным нулю, а направление не определено.
Def. Два направленных отрезка и считаются равными, если они сонаправлены и имеют равные длины. (Обозначают ).
Def. Множество всех равных направленных отрезков называется вектором (или свободным вектором).
Так понимаемый вектор называется свободным, поскольку он представляется направленным отрезком независимо от того, от какой точки тот отложен. Равные направленные отрезки и , отложенные от разных точек представляют один и тот же вектор. Поэтому говорят: – это вектор , отложенный от точки А.
Def. Направление равных направленных отрезков называется направлением вектора, а их модуль – модулем вектора.
Таким образом, любой направленный отрезок однозначно определяет вектор, а вектор – это класс равных направленных отрезков.
Def. Если , то вектор называется единичным вектором или ортом. Def. Множество нулевых отрезков называется нулевым вектором . Его длина равна нулю, а направление не определено.
Def. Вектор называется противоположным вектору , если они имеют равные модули и противоположно направлены.
Т.е. если вектор , то вектор
Def. Сонаправленные и противоположно направленные векторы называются коллинеарными. Обозначают. Нулевой вектор считается коллинеарным любому вектору.
Def. Три (или более) вектора называются компланарными, если они параллельны некоторой плоскости.
Линейные операции над векторами и их свойства
Def. Пусть даны два вектора и . Из произвольной точки пространства отложим и . Тогда есть направленный отрезок и значит, определяет вектор , который называют суммой векторов и (рис. 10.3). Пишут:
Покажем, что вектор не зависит от выбора точки O. Для этого выберем другую точку. Пусть Тогда – параллелограмм. Аналогично, – параллелограмм – параллелограмм , т.е. они определяют один и тот же вектор .
Способ сложения векторов, изложенный выше (рис. 10.3), называется правилом треугольника. Можно также использовать правило параллелограмма (рис. 10.5).
Доказательство свойств 1-2 представлено на рис. 10.6, 10.7. Свойства 3-4 вытекают непосредственно из определения суммы векторов.
Def. Произведением вектора на число называется вектор , удовлетворяющий следующим условиям:
1) векторы и сонаправлены, если и противоположно направлены, если ;
2) .
Произведение на число 0 есть нулевой вектор. Пишут:
$newcommand{updownarrows}{uparrow!downarrow}$
Правило треугольника
Чтобы получить сумму векторов $vec{a}$ и $vec{b}$, нужно от
какой-либо точки $A$ отложить вектор $overrightarrow{AB}=vec{a}$,
затем от точки $B$ отложить вектор $overrightarrow{BC}=vec{b}$.
Вектор $overrightarrow{AC}$ называется суммой векторов $vec{a}$ и $vec{b}$.
$vec{a}+vec{b}=overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$
Определение
Суммой двух векторов называется вектор, полученный по правилу треугольника.
Теорема
Определение суммы векторов корректно, то есть сумма векторов не зависит
от выбора точки $A$.
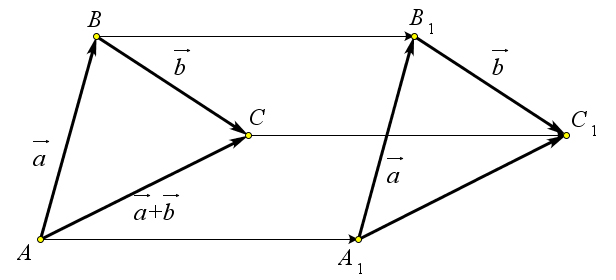
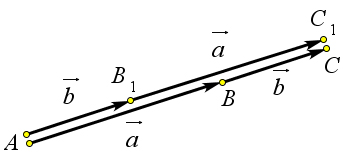
Доказательство
Докажем, что если отложить вектор $a$ от точки $A_1$, то есть $overrightarrow{A_1B_1}=vec{a}$, а затем от точки
$B_1$ отложить вектор $overrightarrow{B_1C_1}=vec{b}$, то сумма векторов $overrightarrow{A_1B_1}+overrightarrow{B_1C_1}=overrightarrow{A_1C_1}$
будет равна вектору $overrightarrow{AC}$, то есть $overrightarrow{A_1C_1}=overrightarrow{AC}$ (рис.
ref{pic133}).
Так как $overrightarrow{AB}=overrightarrow{A_1B_1}$, то по теореме ref{133} имеем $overrightarrow{AA_1}=overrightarrow{BB_1}$.
Аналогично из равенства $overrightarrow{B_1C_1}=overrightarrow{BC}$ следует, что
$overrightarrow{BB_1}=overrightarrow{CC_1}$.
Поэтому $overrightarrow{AA_1}=overrightarrow{CC_1}$.
Но из этого равенства по той же теореме ref{133} следует, что
$overrightarrow{A_1C_1}=overrightarrow{AC}$.
Правило параллелограмма
Если $ABCD$ – параллелограмм, то
$overrightarrow{AB}+overrightarrow{AD}=overrightarrow{AC}$
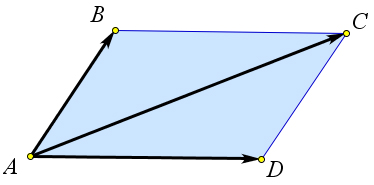
Доказательство
Так как $ABCD$ – параллелограмм, то
$overrightarrow{AD}=overrightarrow{BC}$. Следовательно,
$overrightarrow{AB}+overrightarrow{AC}=overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$.
Свойства сложения векторов
Для любых векторов $vec{a}, vec{b}$ и $vec{c}$
$vec{a}+vec{0}=vec{a}$.
$vec{a}+vec{b}=vec{b}+vec{a}$.
$(vec{a}+vec{b})+vec{c}=vec{a}+(vec{b}+vec{c})$.
Доказательство
Первой свойство очевидно.
Докажем второе свойство.
Возможны два случая: $1)$ векторы $vec{a}$ и $vec{b}$ неколлинеарны, 2) вектора
$vec{a}$ и $vec{b}$ коллинеарны.
Рассмотрим первый случай.
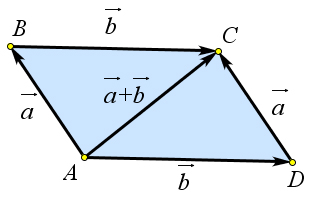
Пусть вектора $vec{a}$ и $vec{b}$ неколлинеарны.
Отложим их от точки $A$: $overrightarrow{AB}=a$ и $overrightarrow{AD}=b$ – и построим
на этих векторах параллелограмм $ABCD$ (рис. ref{pic136} a).
Поскольку $overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}, overrightarrow{AD}+overrightarrow{DC}=overrightarrow{AC},
overrightarrow{AB}=overrightarrow{DC}=vec{a}$ и
$overrightarrow{BC}=overrightarrow{AD}=vec{b}$, то
$vec{a}+vec{b}=vec{b}+vec{a}$.
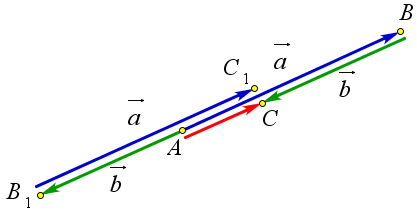
Рассмотрим второй случай.
Пусть вектора $vec{a}$ и $vec{b}$ коллинеарны.
Если вектора $vec{a}$ и $vec{b}$ сонаправлены, то можно их последовательно отложить от точки $A$ двумя способами, то есть $vec{a}+vec{b}=overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$, или
$vec{b}+vec{a}=overrightarrow{AB_1}+overrightarrow{B_1C_1}=overrightarrow{AC_1}$
(рис. ref{pic136} b).
Докажем, что $overrightarrow{AC}=overrightarrow{AC_1}$.
Вектора $overrightarrow{AC}$ и $overrightarrow{AC_1}$ очевидно сонаправлены, кроме того их модули равны $|vec{a}|+|vec{b}|$.
Следовательно, эти вектора равны.
Рассмотрим случай, когда вектора $vec{a}$ и $vec{b}$ противоположно направлены (рис.
ref{pic136} c).
Пусть кроме того $|vec{a}|>|vec{b}|$.
Тогда $vec{a}+vec{b}=overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC}$,
при этом $|overrightarrow{AC}|=|vec{a}|-|vec{b}|$.
C другой стороны $vec{b}+vec{a}=overrightarrow{AB_1}+overrightarrow{B_1C_1}=overrightarrow{AC_1}$,
при этом $|overrightarrow{AC_1}|=|vec{a}|-|vec{b}|$.
Таким образом модули векторов $overrightarrow{AC}$ и $overrightarrow{AC_1}$ равны, кроме того они сонаправлены,
следовательно, $overrightarrow{AC}=overrightarrow{AC_1}$.
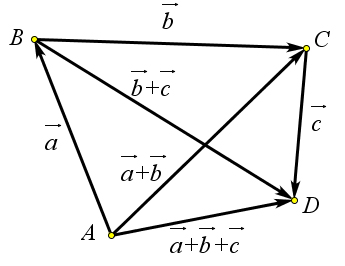
Докажем третий пункт теоремы.
Отложим от точки $A$ вектор $overrightarrow{AB}=vec{a}$, затем от точки $B$ вектор
$overrightarrow{BC}=vec{b}$, а потом от точки $C$ вектор $overrightarrow{CD}=vec{c}$ (рис. ref{pic136} d).
Тогда $(vec{a}+vec{b})+vec{c}=(overrightarrow{AB}+overrightarrow{BC})+overrightarrow{CD}=overrightarrow{AC}+overrightarrow{CD}=overrightarrow{AD}$.
C другой стороны, $vec{a}+(vec{b}+vec{c})=overrightarrow{AB}+(overrightarrow{BC}+overrightarrow{CD})=overrightarrow{AB}+overrightarrow{BD}=overrightarrow{AD}$.
Итак $(vec{a}+vec{b})+vec{c}=vec{a}+(vec{b}+vec{c})$.
Правило цепочки
При любом расположении точек $A_1, A_2, A_3, ldots, A_n$ верно равенство $overrightarrow{A_1A_2}+overrightarrow{A_2A_3}+ldots+overrightarrow{A_{n-1}A_n}=overrightarrow{A_1A_n}$
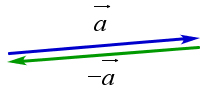
Определение
Два ненулевых вектора называются противоположными, если их длины
равны и они противоположны по направлению. Ноль-вектор считается
противоположным самому себе (рис. ref{pic137}).
Теорема
$vec{a}+(-vec{a})=vec{0}$.
Если $vec{a}+vec{b}=vec{0}$, то $vec{a}=-vec{b}$.
Доказательство
Докажем первый пункт.
Пусть $vec{a}=overrightarrow{AB}$.
Тогда $-vec{a}=overrightarrow{BA}$.
Следовательно, $vec{a}+(-vec{a})=overrightarrow{AB}+overrightarrow{BA}=overrightarrow{AA}=vec{0}$.
Докажем второй пункт.
Пусть $vec{a}+vec{b}=vec{0}$.
Тогда, если $vec{a}=overrightarrow{AB}$, то поскольку $vec{0}=overrightarrow{AA}$, то $vec{b}=overrightarrow{BA}$.
Таким образом, вектора $vec{a}$ и $vec{b}$ равны по модулю и противоположны по направлению, то есть векторы $vec{a}$ и $vec{b}$ противоположны.
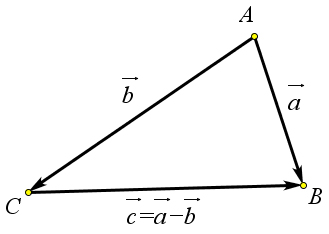
Разность векторов
Разностью векторов $vec{a}$ и $vec{b}$ называется такой вектор
$vec{c}$, что $vec{c}+vec{b}=vec{a}$. Принято обозначать
$vec{c}=vec{a}-vec{b}$.
Следствие
$overrightarrow{AB}-overrightarrow{AC}=overrightarrow{CB}$.
Теорема
Для любых двух векторов $vec{a}$ и $vec{b}$ справедливо равенство
$vec{a}-vec{b}=vec{a}+(-vec{b})$.
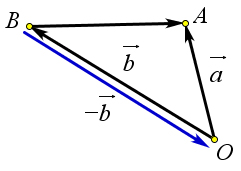
Доказательство
Пусть $vec{c}=overrightarrow{BA}=overrightarrow{OA}-overrightarrow{OB}=vec{a}-vec{b}$.
По правилу треугольника $overrightarrow{BA}=overrightarrow{BO}+overrightarrow{OA}$.
Кроме того $overrightarrow{BO}=-overrightarrow{OB}=-vec{b}$.
Поэтому $vec{a}- vec{b}=overrightarrow{BA}=overrightarrow{BO}+overrightarrow{OA}=overrightarrow{OA}+overrightarrow{BO}=overrightarrow{OA}+(-overrightarrow{OB})=vec{a}+(-vec{b})$.
В данной теме мы подытожим раздел векторы, опишем все действия, которые
можно совершать над векторами и какими свойствами они обладают.
Действия над векторами
Определение
Вектором называется направленный отрезок $overline{A B}$ ,
где точка $A$ — начало, точка
$B$ — конец вектора.
Суммой $overline{a}+overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называют такой третий вектор
$overline{c}$, начало которого совпадает с началом
$overline{a}$, а конец — с концом
$overline{b}$ при условии, что конец вектора
$overline{a}$ и начало вектора
$overline{b}$ совпадают.
Свойства операции сложения:
1° $overline{a}+overline{b}=overline{b}+overline{a}$ — коммутативность
2° $(overline{a}+overline{b})+overline{c}=overline{a}+(overline{b}+overline{c})$ — ассоциативность
3° $overline{a}+overline{0}=overline{a}$
4° $overline{a}+(-overline{a})=overline{0}$
Определение
Разностью $overline{a}-overline{b}$ векторов
$overline{a}$ и
$overline{b}$ называется вектор $overline{c}$
такой, что выполняется условие: $overline{b}+overline{c}=overline{a}$.
Произведением $alpha overline{a}$ вектора
$overline{a}$ на число
$alpha$ называется вектор
$overline{b}$, удовлетворяющий условиям:
- $overline{b} | overline{a}$
- $|overline{b}|=|alpha||overline{a}|$
- $overline{a} uparrow uparrow overline{b}$, если
$alpha>0$,
$overline{a} uparrow downarrow overline{b}$, если
$alpha
Свойства умножения вектора на число:
1° $(alpha pm beta) overline{a}=alpha overline{a} pm beta overline{a}$
2° $alpha(overline{a} pm overline{b})=alpha overline{a} pm alpha overline{b}$
3° $alpha(beta overline{a})=(alpha beta) overline{a}=beta(alpha overline{a})$
4° $1 cdot overline{a}=overline{a}$
5° $-1 cdot overline{a}=-overline{a}$
6° $0 cdot overline{a}=overline{0}$
Определение
Скалярным произведением двух ненулевых векторов $overline{a}$ и
$overline{b}$ называется число, равное произведению
длин этих векторов на косинус угла между ними:
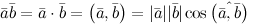
Свойства скалярного произведения:
1° $(overline{a}, overline{b})=(overline{b}, overline{a})$ — симметричность.
2° $(overline{a}, overline{a})=|overline{a}|^{2}$. Обозначается
$(overline{a}, overline{a})=overline{a}^{2}$ и называется скалярный квадрат.
3° Если $overline{a} neq overline{0}$, то 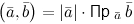
4° Если $overline{a} neq overline{0}$ и $overline{b} neq overline{0}$ и
$(overline{a}, overline{b})=0$, то $overline{a} perp overline{b}$. Верно и обратное утверждение.
5° $(overline{a}+overline{b}, overline{c})=(overline{a}, overline{c})+(overline{b}, overline{c})$
6° $(lambda overline{a}, overline{b})=lambda(overline{a}, overline{b})$
7° $(alpha overline{a}+beta overline{b}, gamma overline{c}+delta overline{d})=alpha gamma(overline{a}, overline{c})+alpha delta(overline{a}, overline{d})+beta gamma(overline{b}, overline{c})+beta delta(overline{b}, overline{d})$
Определение
Векторным произведением ненулевых векторов $overline{a}$ и
$overline{b}$ называется вектор $overline{c}$,
обозначаемый символом $[overline{a}, overline{b}]$ или
$overline{a} times overline{b}$, длина которого
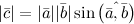 .
.
Свойства векторного произведения:
1° $[overline{a}, overline{b}]=overline{0}$, тогда и только тогда, когда
$overline{a} | overline{b}$
2° $[overline{a}, overline{b}]=-[overline{b}, overline{a}]$
3° Модуль векторного произведения $|[overline{a}, overline{b}]|$
равен площади параллелограмма, построенного на заданных векторах $overline{a}$ и
$overline{b}$ (рис. 2), т.е.
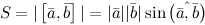
4° $[lambda overline{a}, overline{b}]=[overline{a}, lambda overline{b}]=lambda[overline{a}, overline{b}]$
5° $left[overline{a}_{1}+overline{a}_{2}, overline{b}right]=left[overline{a}_{1}, overline{b}right]+left[overline{a}_{2}, overline{b}right] ;left[overline{a}, overline{b}_{1}+overline{b}_{2}right]=left[overline{a}, overline{b}_{1}right]+left[overline{a}, overline{b}_{2}right]$
Определение
Смешанным произведением трех векторов $overline{a}$,
$overline{b}$, $overline{c}$
называется число, равное скалярному произведению вектора $overline{a} times overline{b}$
на вектор $overline{c}$: $(overline{a}, overline{b}, overline{c})=([overline{a}, overline{b}], overline{c})$
Свойства смешанного произведения:
1° $(overline{a}, overline{b}, overline{c})=(overline{a},[overline{b}, overline{c}])$
2° $(overline{a}, overline{b}, overline{c})=(overline{b}, overline{c}, overline{a})=(overline{c}, overline{a}, overline{b})=-(overline{b}, overline{a}, overline{c})=-(overline{c}, overline{b}, overline{a})=-(overline{a}, overline{c}, overline{b})$
3° Три вектора компланарны тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})=0$
4° Тройка векторов является правой тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})>0$.
Если же $(overline{a}, overline{b}, overline{c})
5° $(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})$
6° $left(overline{a}_{1}+overline{a}_{2}, overline{b}, overline{c}right)=left(overline{a}_{1}, overline{b}, overline{c}right)+left(overline{a}_{2}, overline{b}, overline{c}right)$
7° $left(overline{a}, overline{b}_{1}+overline{b}_{2}, overline{c}right)=left(overline{a}, overline{b}_{1}, overline{c}right)+left(overline{a}, overline{b}_{2}, overline{c}right)$
8° $left(overline{a}, overline{b}, overline{c}_{1}+overline{c}_{2}right)=left(overline{a}, overline{b}, overline{c}_{1}right)+left(overline{a}, overline{b}, overline{c}_{2}right)$
9° $([overline{a}, overline{b}], overline{c})=overline{b}(overline{a}, overline{c})-overline{a}(overline{b}, overline{c}) ;(overline{a},[overline{b}, overline{c}])=overline{b}(overline{a}, overline{c})-overline{c}(overline{a}, overline{b})$
10° Тождество Якоби: $(overline{a},[overline{b}, overline{c}])+(overline{b},[overline{c}, overline{a}])+(overline{c},[overline{a}, overline{b}])=0$
Читать дальше: примеры решения задач с векторами.
Вы поняли, как решать? Нет?
- Главная
- Справочник
- Геометрия
- Вектора
- Сложение и вычитание векторов
Векторы: ( vec{a} ), ( vec{b} ), ( vec{c} ), ( vec{u_1} ), ( vec{u_2},;ldots; )
Нулевой вектор: ( vec{0} )
Координаты векторов: ( {X_1} ), ( {Y_1} ), ( {Z_1} ), ( {X_2} ), ( {Y_2} ), ( {Z_2} )
Определение 1 Если точка ( A ) начала какого-либо вектора ( overrightarrow{a} ), то говорят, что вектор ( overrightarrow{a} ) отложен от точки ( A ) (рис. 1).

Теорема 1 От любой точки ( K ) можно отложить вектор единственный ( overrightarrow{a} ).
Существование: Имеем два следующих случая:
Вектор ( overrightarrow{a} ) — нулевой.
Здесь получаем, что искомый нами вектор совпадает с вектором ( overrightarrow{KK} ).
Вектор ( overrightarrow{a} ) не является нулевым.
Пусть точка ( A ) является началом вектора ( overrightarrow{a} ), а точкой ( B ) — конец вектора ( overrightarrow{a} ). Проведем через точку ( K ) прямую ( b ) параллельную вектору ( overrightarrow{a} ). Будем откладывать на прямой отрезки ( left|KLright|=|AB| ) и ( left|KMright|=|AB| ). Рассмотрим векторы ( overrightarrow{KL} ) и ( overrightarrow{KM} ). Из этих двух векторов нужный нам вектор — вектор, сонаправленный с вектором ( overrightarrow{a} ) (рис.2)

Рисунок 2.
Из данного выше построения сразу же будет следовать единственность данного вектора.
Сумма векторов. Сложение векторов. Правило треугольника
Суммой двух векторов ( vec{a} ) и ( vec{b} ) называется третий вектор ( vec{c} ), проведенный из начала ( vec{a} ) к концу ( vec{b} ), если начало вектора ( vec{b} ) совпадает с концом вектора ( vec{a} ).
Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.
( vec{c} = vec{a} + vec{b} )

Суммой нескольких векторов ( vec{a_1} ),( vec{a_2} ), ( vec{a_3},;ldots ) называется вектор ( vec{c} ), получающийся в результате последовательного сложения данных векторов.
Такая операция выполняется по правилу многоугольника.
( vec{c} = vec{a_1} + vec{a_2} + vec{a_3} + ldots + vec{a_n} )

Коммутативный закон сложения
( vec{a} + vec{b} = vec{b} + vec{a} )
Ассоциативный закон сложения
( left( {vec{a} + vec{b}} right) + vec{c} = vec{a} + left( {vec{b} + vec{c}} right) )
Сумма векторов в координатах
При сложении двух векторов соответствующие координаты складываются.
( vec{a} + vec{b} = left( {{X_1} + {X_2},{Y_1} + {Y_2},{Z_1} + {Z_2}} right) )
Отметим несколько свойств сложения двух векторов:
Для произвольного вектора ( overrightarrow{a} ) выполняется равенство
[ overrightarrow{a}+overrightarrow{0}=overrightarrow{a} ]
Для произвольных точек ( A, B и C ) справедливо следующее равенство
[ overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC} ]
Замечание Таким способом также можно строить сумму любого числа векторов. Тогда оно будет носить название правила многоугольника.

Разность векторов. Вычитание векторов
Разностью двух векторов ( vec{a} ) и ( vec{b} ) называется вектор ( vec{c} ) при условии:
( vec{c} = vec{a} — vec{b} ), если ( vec{c} + vec{b} = vec{a} )
Разность векторов ( vec{a} ) и ( vec{b} ) равна сумме вектора ( vec{a} ) и противоположного вектора ( -vec{b} ):
( vec{a} — vec{b} = vec{a} + left( -vec{b} right) )

Разность двух одинаковых векторов равна нулевому вектору :
( vec{a} — vec{a} = vec{0} )
Длина нулевого вектора равна нулю:
( left| vec{0} right| = 0 )
Разность векторов в координатах
При вычитании двух векторов соответствующие координаты также вычитаются.
( vec{a} — vec{b} = left( {{X_1} — {X_2},{Y_1} — {Y_2},{Z_1} — {Z_2}} right) )
Умножение вектора на число
Пусть нам дан вектор ( overrightarrow{a } ) и действительное число ( k ).
Определение Произведением вектора ( overrightarrow{a } ) на действительное число ( k ) называется вектор ( overrightarrow{b } ) удовлетворяющий следующим условиям:
Длина вектора ( overrightarrow{b } ) равна ( left|overrightarrow{b }right|=left|kright||overrightarrow{a }| );
Векторы ( overrightarrow{a } ) и ( overrightarrow{b } ) сонаправлены, при ( kge 0 ) и противоположно направлены, если ( kle 0 )
Обозначение: ( overrightarrow{b }=koverrightarrow{a } ).
Пусть даны векторы ( overrightarrow{a} ) и ( overrightarrow{b} ). Построить вектор ( overrightarrow{a}-overrightarrow{b} ).
Построим произвольную точку ( O ) и отложим от нее векторы ( overrightarrow{OA}=overrightarrow{a} ) и ( overrightarrow{OB}=overrightarrow{b} ). Соединив точку ( B ) с точкой ( A ), получим вектор ( overrightarrow{BA} ).

По правилу треугольника для построения суммы двух векторов видим, что
[ overrightarrow{OB}+overrightarrow{BA}=overrightarrow{OA} ]
То есть
[ overrightarrow{b}+overrightarrow{BA}=overrightarrow{a} ]
Из определения 2, получаем, что
[ overrightarrow{a}-overrightarrow{b}=overrightarrow{BA} ]
( overrightarrow{a}-overrightarrow{b}=overrightarrow{BA} ).
Уровень8 класс ПредметМатематика СложностьПростая
Дан прямоугольный параллелепипед ( ABCDA_1B_1C_1D_1 ). Доказать, что ( overrightarrow{AB}+overrightarrow{AD}+overrightarrow{AA_1}=overrightarrow{AC_1} )
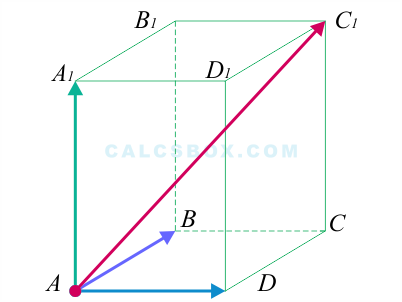
Воспользуемся свойством правила треугольника ( overrightarrow{AB}+overrightarrow{BC}=overrightarrow{AC} ), получим:
[ overrightarrow{AC_1}=overrightarrow{AD}+overrightarrow{DC}+overrightarrow{CC_1} ]
Так как ( overrightarrow{DC}=overrightarrow{AB}, overrightarrow{CC_1}=overrightarrow{AA_1} )
То есть
[ overrightarrow{AC_1}=overrightarrow{AB}+overrightarrow{AD}+overrightarrow{AA_1} ]
ч. т. д.
Уровень8 класс ПредметМатематика СложностьПростая
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
