Какие свойства сложения и умножения выражают равенства

Умножение, сложение, вычитание и деление — основные операции с целыми числами. Результаты этих операций с любыми целыми числами обладают рядом характеристик. Иначе говоря, операции умножения, сложения, вычитания и деления целых чисел обладают свойствами. Данная статья посвящена рассмотрению основных свойств умножения, сложения, вычитания и деления целых чисел.
Сложение целых чисел. Основные свойства
Все свойства сложения натуральных чисел оказываются справедливы и для целых чисел. Ведь множество целых чисел ℤ включает в себя множество натуральных чисел ℕ. Приведем ниже основные свойства сложения.
Коммутативное свойство сложения
Переместительное (коммутативное свойство) или переместительный закон.
От перемены мест слагаемых сумма не меняется.
a+b=b+a
Согласно этому свойству, справедливо равенство:
35+251=251+35
Свойство коммутативности работает вне зависимости от знака.
-528+3700=3700+-528
Ассоциативное свойство сложения
Сочетательное (ассоциативное свойство) или сочетательный закон.
Сложение целого числа с суммой двух целых чисел эквивалентно сложению суммы двух первых чисел с третьим.
a+b+c=a+b+c
Примечание: данное свойство применимо и для большего количества слагаемых.
Вот несколько примеров. Согласно свойству ассоциативности справедливы равенства:
64+81+(-49)=64+81+(-49)=64+81+(-49);
(128+(-75))+96=128+((-75)+96).
Свойства сложения, связанные с числом 0
1. Число нуль — нейтральный по сложению элемент.
Прибавление нуля к любому целому числу не меняет этого числа.
a+0=a
2. Сумма любого целого числа и противоположного ему числа равна нулю.
a+(-a)=0
Умножение целых чисел. Основные свойства
Как и в случае со сложением, все свойства умножения натуральных чисел переносятся на целые числа.
Для умножения также действуют переместительный и сочетательный (коммутативный и ассоциативный) законы.
Переместительное свойство умножения
От перемены мест множителей произведение не меняется.
a·b=b·a
Приведем пример. Очевидно, что произведение целых чисел 2·3 эквивалентно произведению 3·2.
Сочетательное свойство умножения
Сочетательное свойство для умножения эквивалентно сочетательному свойству сложения. В буквенном виже оно записывается следующим образом:
a·(b·c)=(a·b)·c
a, b, c — произвольные целые числа.
Примечание: данное свойство применимо и для большего количества множителей.
В соответствии с этим свойством можно говорить о справедливости следующих равенств:
-12·3·8=-12·3·8;
119·((-251)·36)=(119·(-251))·36.
Умножение числа на нуль
Результатом умножения любого целого числа на нуль является число нуль.
a·0=0
Справедливо и обратное: произведение двух целых чисел a и b равно нулю, если хотя бы один из множителей равен нулю.
a·b=0 если a=0 или b=0.
Умножение числа на единицу
Умножение любого целого числа на единицу дает в результате это число. Иными словами, умножение на единицу не изменяет умножаемое число.
a·1=a
Распределительное свойство умножения относительно суммы.
Произведение целого числа a на сумму двух чисел b и c равно сумме произведений a·b и a·c.
a·(b+c)=a·b+a·c
Данное свойство часто используется при упрощении выражений, одновременно содержащих как операции сложения, так и умножения.
В совокупности с ассоциативным свойством и распределительным законом можно легко расписать произведение целого числа на сумму из более чем трех слагаемых, а также произведение сумм.
Вычитание целых чисел. Основные свойства
Вычитание — действие, обратное сложению. Число c является разностью двух чисел a и b тогда, когда сумма b+c равна a. Можно сказать, что разность чисел a и b — это сумма чисел a и -b. Свойства вычитания являются следствием свойств сложения и умножения.
Основные свойства вычитания
- Вычитание чисел не обладает переместительным свойством за исключением случая, когда a=b. a-b≠b-a.
- Разность целых чисел, равных друг другу: a-a=0.
- Вычитание суммы двух чисел из другого числа: a-(b+c)=a-b-c.
- Вычитание целого числа из суммы: a+b-c=a-c+b=a+(b-c).
- Распределительное свойство умножения относительно вычитания: a·(b-c)=a·b-a·c.
Деление целых чисел. Основные свойства
Деление — операция, обратная умножению. Число c называется частным от деления чисел a и b, когда произведение b·c равно a. Запишем основные свойства деления целых чисел.
Основные свойства деления
- Деление на нуль невозможно.
- Деление нуля на число: 0a=0.
- Деление равных чисел: aa=1.
- Деление на единицу: a1=a.
- Для деления переместительное свойства не выполняется: ab≠ba.
- Деление суммы и разности на число: a±bc=ac±bc.
- Деление произведения на число: a·bc=ac·b, если a делится на c; a·bc=a·bс, если b делится на c; a·bc=a·bс=ac·b, если a и b делятся на c.
- Деление числа на произведение: ab·c=ab·1c=ac·1b.
В нашей жизни есть законы, которые надо соблюдать. Соблюдение законов гарантирует стабильность и гармоничное развитие. Несоблюдение же законов приводит к печальным последствиям.
У математики есть свои законы, которые тоже следует соблюдать. Несоблюдение законов математики приводит в лучшем случае к тому, что оценка учащегося снижается, а в худшем случае приводит к тому, что падают самолёты, зависают компьютеры, улетают крыши домов от сильного ветра, снижается качество связи и тому подобные нехорошие явления.
Законы математики состоят из простых свойств. Эти свойства нам знакомы со школы. Но не мешает вспомнить их ещё раз, а лучше всего записать или выучить наизусть.
В данном уроке мы рассмотрим лишь малую часть законов математики. Их нам будет достаточно для дальнейшего изучения математики.
Переместительный закон сложения
Переместительный закон сложения говорит о том, что от перестановки мест слагаемых сумма не изменяется. Действительно, прибавьте пятерку к двойке — получите семёрку. И наоборот, прибавьте двойку к пятерке — опять получите семёрку:
5 + 2 = 7
2 + 5 = 7
Если положить на одну чашу весов 10 килограмм яблок и на другую чашу так же положить 10 килограмм яблок, то весы выровнятся, и не важно, что яблоки в пакетах лежат вразброс. Если мы возьмём пакет с весов и перемешаем яблоки находящиеся в нём, словно шары в лотерейном мешке, пакет всё так же будет весить 10 килограмм. От перестановки мест слагаемых сумма не изменится. Слагаемые в данном случае это яблоки, а сумма это итоговый вес.
Таким образом, между выражениями 5 + 2 и 2 + 5 можно поставить знак равенства. Это будет означать, что их сумма равна:
5 + 2 = 2 + 5
7 = 7
Полагаем что, вы изучили один из предыдущих уроков, который назывался выражения, поэтому мы без тени смущения запишем переместительный закон сложения с помощью переменных:
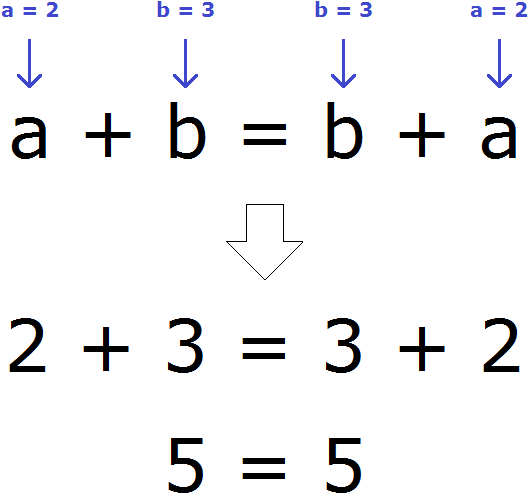
a + b = b + a
Записанный переместительный закон сложения будет работать для любых чисел. Например, возьмём любых два числа. Пусть а = 2, b = 3. Мы присвоили переменным a и b значения 2 и 3 соответственно. Эти значения отправятся в главное выражение a + b = b + a и подставятся куда нужно. Число 2 подставится вместо а, число 3 место b
Сочетательный закон сложения
Сочетательный закон сложения говорит о том, что результат сложения нескольких слагаемых не зависит от порядка действий. Этот закон позволяет группировать слагаемые для удобства их вычислений.
Рассмотрим сумму из трёх слагаемых:
2 + 3 + 5
Чтобы вычислить данное выражение, можно сначала сложить числа 2 и 3 и полученный результат сложить с числом 5. Для удобства сумму чисел 2 и 3 можно заключить в скобки, указывая тем самым, что эта сумма будет вычислена в первую очередь:
2 + 3 + 5 = (2 + 3) + 5 = 5 + 5 = 10
Либо можно сложить числа 3 и 5, затем полученный результат сложить с числом 2
2 + 3 + 5 = 2 + (3 + 5) = 2 + 8 = 10
Видно, что в обоих случаях получается один и тот же результат.
Таким образом, между выражениями (2 + 3) + 5 и 2 + (3 + 5) можно поставить знак равенства, поскольку они равны одному и тому же значению:
(2 + 3) + 5 = 2 + (3 + 5)
10 = 10
Запишем сочетательный закон сложения с помощью переменных:
(a + b) + c = a + (b + c)
Переместительный закон умножения
Переместительный закон умножения говорит о том, что если множимое и множитель поменять местами, то произведение не изменится. Давайте проверим так ли это. Умножим пятерку на двойку, а затем наоборот двойку на пятерку.
5 × 2 = 10
2 × 5 = 10
В обоих случаях получается один и тот же результат, поэтому между выражениями 5 × 2 и 2 × 5 можно поставить знак равенства, поскольку они равны одному и тому же значению:
5 × 2 = 2 × 5
10 = 10
Запишем переместительный закон умножения с помощью переменных:
a × b = b × a
Для записи законов в качестве переменных необязательно использовать именно буквы a и b. Можно использовать любые другие буквы, например c и d или x и y. Тот же переместительный закон умножения можно записать следующим образом:
x × y = y × x
Сочетательный закон умножения
Сочетательный закон умножения говорит о том, что если выражение состоит из нескольких сомножителей, то произведение не будет зависеть от порядка действий.
Рассмотрим следующее выражение:
2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Сначала можно перемножить числа 2 и 3, и полученный результат умножить на 4:
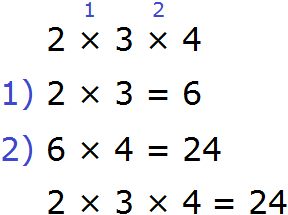
Либо сначала можно перемножить числа 3 и 4, и полученный результат перемножить с числом 2
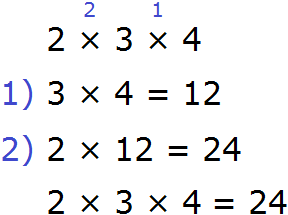
Таким образом, между выражениями (2 × 3) × 4 и 2 × (3 × 4) можно поставить знак равенства, поскольку они равны одному и тому же значению:
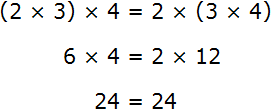
Запишем сочетательный закон умножения с помощью переменных:
a × b × с = (a × b) × с = a × (b × с)
Пример 2. Найти значение выражения 1 × 2 × 3 × 4
Данное выражение можно вычислять в любом порядке. Вычислим его слева направо в порядке следования действий:
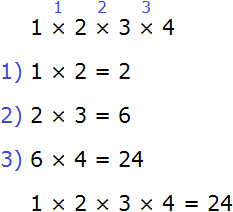
Распределительный закон умножения
Распределительный закон умножения позволяет умножить сумму на число или число на сумму.
Рассмотрим следующее выражение:
(3 + 5) × 2
Мы знаем, что сначала надо выполнить действие в скобках. Выполняем:
(3 + 5) = 8
В главном выражении (3 + 5) × 2 выражение в скобках заменим на полученную восьмёрку:
8 × 2 = 16
Получили ответ 16. Этот же пример можно решить с помощью распределительного закона умножения. Для этого каждое слагаемое, которое в скобках, нужно умножить на 2, затем сложить полученные результаты:
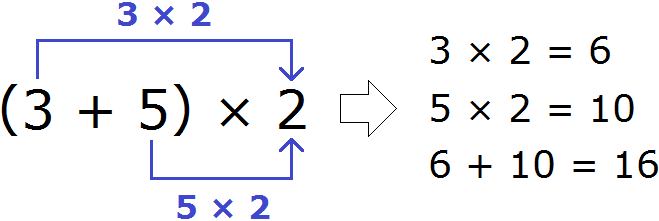
Мы рассмотрели распределительный закон умножения слишком развёрнуто и подробно. В школе этот пример записали бы очень коротко. К такой записи тоже надо привыкать. Выглядит она следующим образом:
(3 + 5) × 2 = 3 × 2 + 5 × 2 = 6 + 10 = 16
Или ещё короче:
(3 + 5) × 2 = 6 + 10 = 16
Теперь запишем распределительный закон умножения с помощью переменных:
(a + b) × c = a × c + b × c
Давайте внимательно посмотрим на начало этого распределительного закона умножения. Начало у него выглядит так: (a + b) × c.
Если рассматривать выражение в скобках (a + b), как единое целое, то это будет множимое, а переменная с будет множителем, поскольку соединены они знаком умножения ×
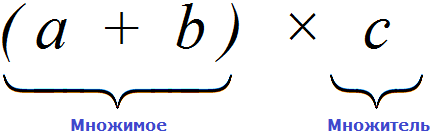
Из переместительного закона умножения мы узнали, что если множимое и множитель поменять местами, то произведение не изменится.
Если множимое (a + b) и множитель c поменять местами, то получим выражение c × (a + b). Тогда получится, что мы умножаем переменную c на сумму (a + b). Для выполнения такого умножения, опять же применяется распределительный закон умножения. В данном случае переменную c нужно умножить на каждое слагаемое в скобках:
c × (a + b) = c × a + c × b
Пример 2. Найти значение выражения 5 × (3 + 2)
Умножим число 5 на каждое слагаемое в скобках и полученные результаты сложим:
5 × (3 + 2) = 5 × 3 + 5 × 2 = 15 + 10 = 25
Пример 3. Найти значение выражения 6 × (5 + 2)
Умножим число 6 на каждое слагаемое в скобках и полученные результаты сложим:
6 × (5 + 2) = 6 × 5 + 6 × 2 = 30 + 12 = 42
Если в скобках располагается не сумма, а разность, то сначала нужно умножить множимое на каждое число, которое в скобках. Затем из полученного первого числа вычесть второе число. В принципе, ничего нового.
Пример 4. Найти значение выражения 5 × (6 − 2)
Умножим 5 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
5 × (6 − 2) = 5 × 6 − 5 × 2 = 30 − 10 = 20
Пример 5. Найти значение выражения 7 × (3 − 2)
Умножим 7 на каждое число в скобках. Затем из полученного первого числа вычтем второе число:
7 × (3 − 2) = 7 × 3 − 7 × 2 = 21 − 14 = 7
Задания для самостоятельного решения
Задание 1. Найдите значение выражения, используя распределительный закон умножения:
3 × (7 + 8)
Решение:
3 × (7 + 8) = 3 × 7 + 3 × 8 = 21 + 24 = 45
Задание 2. Найдите значение выражения, используя распределительный закон умножения:
5 × (6 + 8)
Решение:
5 × (6 + 8) = 5 × 6 + 5 × 8 = 30 + 40 = 70
Задание 3. Найдите значение выражения, используя порядок выполнения действий:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
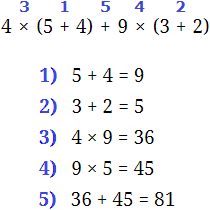
Задание 4. Найдите значение выражения, используя распределительный закон умножения:
4 × (5 + 4) + 9 × (3 + 2)
Решение:
4 × (5 + 4) + 9 × (3 + 2) = 4 × 5 + 4 × 4 + 9 × 3 + 9 × 2 = 20 + 16 + 27 + 18 = 81
Задание 5. Найдите значение выражения, используя распределительный закон умножения:
16 × (2 + 7) + 5 × (4 + 1)
Решение:
16 × (2 + 7) + 5 × (4 + 1) = 16 × 2 + 16 × 7 + 5 × 4 + 5 × 1 = 32 + 112 + 20 + 5 = 169
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже


Навигация по записям
Например, пусть Используя условия III, IV и V, можно выписать следующую цепочку равенств:
таким образом,
ТЕОРЕМА 2.1. Сложение натуральных чисел ассоциативно, т. е. для любых натуральных а, b, с
Доказательство. Зафиксируем произвольные натуральные числа а и b. Тогда формула (1) определяет предикат от одной свободной переменной с, обозначим его . Доказательство проводится индукцией по натуральной переменной с.
Базис индукции: А(0) истинно, поскольку верно равенство
Индукционный шаг. Предположим, что для некоторого натурального истинно , т. е. верна формула
и докажем, что тогда истинно , т. е. верна формула
В самом деле,
Согласно принципу индукции, предикат истинен для любого натурального с. Поскольку при доказательстве фиксировались произвольные а и , то формула (1) верна для любых натуральных а и b.
ОПРЕДЕЛЕНИЕ. Алгебра называется аддитивным моноидом натуральных чисел.
ЛЕММА 2.2. Для любых натуральных а и b
Доказательство. Проведем доказательство индукцией по b. Зафиксируем произвольное натуральное число а.
Обозначим через предикат, определяемый формулой (1). Условимся в этой лемме и в дальнейшем в аналогичных случаях говорить, что является и обозначением соответствующей формулы.
Легко видеть, что верна формула
Предположим, что для некоторого натурального числа верна формула
и покажем, что верна формула . В самом деле,
(по аксиоме IV);
(по индуктивному предположению);
(по аксиоме IV).
Согласно принципу индукции, формула верна для любого натурального b. Так как при доказательстве фиксировалось произвольное значение а, то формула (1) верна для любых натуральных а и b.
ТЕОРЕМА 2.3. Сложение натуральных чисел коммутативно, т. е. для любых натуральных а, b
Доказательство проводится индукцией по b. Докажем сначала, что верна формула
Проведем индукцию по о.. Очевидно, формула верна при Далее, если для некоторого натурального числа
то
Следовательно, по принципу индукции, формула А (0) верна для любого а.
Зафиксируем произвольное а. Обозначим через А(b) предикат, определяемый формулой (1). Предположим, что для некоторого натурального числа верна формула
тогда
(по аксиоме IV);
(по индуктивному предположению);
(по аксиоме IV);
(по лемме 2.2),
т. е. верна формула . Согласно принципу индукции, формула верна для любого 6. Поскольку фиксировалось произвольное значение а, то формула (I) верна для любых натуральных а и 6.
ТЕОРЕМА 2.4 (ЗАКОН СОКРАЩЕНИЯ ДЛЯ СЛОЖЕНИЯ). Для любых натуральных а, b, с
Доказательство (проводится индукцией по с; при этом фиксируются произвольные значения а и b). Рассмотрим формулу
Так как , то верно, что
т. е. верна формула А(0).
Предположим, что для некоторого натурального числа
и покажем, что тогда верна формула По аксиоме IV,
Далее, по аксиоме II,
Из того, что и (3) — верные формулы, следует, что верна формула
На основании (2) и (4) заключаем, что верна формула
Согласно принципу индукции, формула А(с) верна для любого натурального с. Так как а и b фиксировались произвольно, утверждение (1) верно для любых натуральных а, b, с.
СЛЕДСТВИЕ 2.5. Для любых натуральных а и b, если то
ТЕОРЕМА 2.6. Для любого натурального числа а либо либо существует такое натуральное число b, что
Доказательство. Рассмотрим формулу
Доказательство этой формулы проводится индукцией по а. Очевидно, формула верна при Предположим, что для некоторого натурального числа верна формула
Надо показать, что верна формула
Эта формула действительно верна, так как второй член дизъюнкции — истинная формула (при ). Согласно принципу индукции, формула верна для любого натурального а.
СЛЕДСТВИЕ 2.7. Для любых натуральных а и b, если или то
Доказательство. Предположим, что . Тогда, по теореме 2.6, существует такое натуральное с, что . В силу аксиомы IV
По аксиоме следовательно,
СЛЕДСТВИЕ 2.8. Для любых натуральных а и b, если а то
ТЕОРЕМА 2.9. Для любых натуральных выполняется одно и только одно из трех условий:
(для некоторого );
(для некоторого ).
Доказательство. Из следствия 2.5 вытекает, что не может выполняться более чем одно из трех условий.
В самом деле, если бы выполнялись условия , то что невозможно по следствию 2.5. Если бы выполнялись условия (а) и (7), то что невозможно. Если бы выполнялись условия , то что также противоречит следствию 2.5.
Теперь покажем, что выполняется хотя бы одно из условий . Фиксируем произвольное натуральное число а и обозначим через дизъюнкцию условий . Докажем индукцией по b верность формулы Верна формула . В самом деле, если , то либо либо а . Если где Следовательно, при выполняется условие (а) или условие
Предположим, что для некоторого числа верна формула
и покажем, что тогда верна формула . В самом деле, если выполняется условие (Р). Если выполняется условие (Р). Если же , то . В этом случае если то и, по аксиоме II, — выполняется условие (а). Так как , то, по теореме 2.6, существует такое, что . Если , то и из равенства по аксиоме II получаем — выполняется условие (y). Итак, в любом случае верна формула Согласно принципу индукции, формула верна для любого натурального b. Поскольку а фиксировалось произвольно, то утверждение теоремы верно для любых натуральных а и b.
ОПРЕДЕЛЕНИЕ. Разностью двух натуральных чисел а и b называется такое натуральное число k, что
Из теоремы 2.9 следует, что разность двух натуральных чисел а и b существует в том случае, когда выполнено условие (а) (при этом или . В случае выполнения условия (Р) разность чисел а и b не существует.
Легко показать, что если разность чисел а и b существует, то она единственна. В самом деле, если , то откуда, по закону сокращения для сложения, следует, что .
Единственное натуральное число, являющееся разностью чисел а и b, обозначают а — b.
Ranina
Мастер
(1157)
12 лет назад
ну, первое:
От перестановки мест слагаемых (множителей) сумма (произведение) не меняется.
второе: (a + b) + c = a + (b + c), (ab)c = a(bc).
третье : : c(a + b) = ca + cb.
Сергей
Знаток
(430)
12 лет назад
а*в=в*а; а+в=в+а; — переместительное
а (в+с) =ав+ас — распределительное
(a + b) + с = a + (b + c); ab)с = a(bc) — Сочетательное
СергейЗнаток (430)
12 лет назад
Прошу прощения
(a + b) + с = a + (b + c); (ab)с = a(bc) — Сочетательный
Павел Чупраков
Знаток
(254)
4 года назад
a + b = b + a (переместительный закон сложения).
(a + b) + c = a + (b + c) (сочетательный закон сложения).
ab = ba (переместительный закон умножения).
(ab)c = a(bc) (сочетательный закон умножения).
a(b + c) = ab + ac (распределительный закон умножения относительно сложения).
Гала
Ученик
(210)
3 года назад
1 Переместительный закон сложения и умножения:
От перемены мест слагаемых сумма не меняется. (Значение суммы при перестановке двух слагаемых не меняется.) a + b = b + a = с
От перемены мест множителей произведение не меняется. (Значение произведения при перестановке множителей не меняется.) a x b = b x a = с
2 Сочетательное свойство сложения и умножения: Для любых чисел a, b и c верны равенства: (a + b) + c = a + (b + c) и (ab)c = a(bc)
3 Распределительное свойство умножения: Для любых чисел a, b и c верны равенства: (a + b) + c = a + (b + c) и (ab)c = a(bc)
Из переместительного и сочетательного свойств сложения следует, что в любой сумме можно как угодно переставлять слагаемые и произвольным образом объединять их в группы.
Точно также из переместительного и сочетательного свойств умножения следует, что в любом произведении можно как угодно переставлять множители и произвольным образом объединять их в группы.
Распределительное свойство справедливо и в том случае, когда число умножается на сумму трех и более слагаемых.
Для любых чисел a, b, c и d, верно равенство: a(b + c + d) = ab + ac + ad
4 правило деления суммы на число:
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и полученные результаты сложить: (а + b) : с = а : с + b : с
5 Правило вычитания числа из суммы: 1. Чтобы вычесть сумму из числа, можно из него вычесть одно слагаемое, а из полученного результата (разности) вычесть второе слагаемое. Например: 126 — (56 + 30) = (126 — 56) — 30 = 40. В общем виде: а — (Ь + с) = (а — Ь) — с. Правило 2. Чтобы вычесть число из суммы, можно вычесть его из одного из слагаемых и к результату прибавить второе слагаемое. Правило 2 можно использовать при вычислении натуральных чисел только в случае, если одно из слагаемых больше вычитаемого числа. Например: (71 + 7) — 51 = (71 — 51) + 7 = 20 + 7 = 27, но нельзя (71 + 7) — 51 = (7 — 51) + 71,так как разность (7 — 51) — ненатуральное число. В общем виде: (а + Ь) — с = (а — с) + Ь.
6 правило вычитание суммы из числа
а-(х+у) = а-х-у. Если перед скобкой стоит знак «-«, то знаки в скобке меняются на противоположный
Данил Ларионов
Ученик
(124)
2 года назад
a + b = b + a (переместительный закон сложения).
(a + b) + c = a + (b + c) (сочетательный закон сложения).
ab = ba (переместительный закон умножения).
(ab)c = a(bc) (сочетательный закон умножения).
a(b + c) = ab + ac (распределительный закон умножения относительно сложения).
Елисей Ивкин
Ученик
(124)
2 года назад
От перестановки мест слагаемых (множителей) сумма (произведение) не меняется.
второе: (a + b) + c = a + (b + c), (ab)c = a(bc).
третье : : c(a + b) = ca + cb.
Андрей Тульский
Ученик
(108)
2 года назад
a + b = b + a (переместительный закон сложения).
(a + b) + c = a + (b + c) (сочетательный закон сложения).
ab = ba (переместительный закон умножения).
(ab)c = a(bc) (сочетательный закон умножения).
a(b + c) = ab + ac (распределительный закон умножения относительно сложения).
