Какие свойства системы характеризует энтропия
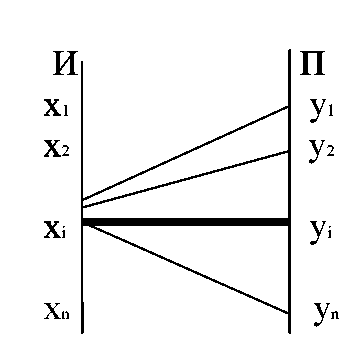
Физическим смыслом понятия энтропии является мера хаоса в системе; мера той энергии, которая рассеивается в виде тепла и не превращается в работу («связанная энергия«). Энтропия является функцией состояния системы и не зависит от пути перехода. Ее изменение определяется только начальным и конечным состоянием. Размерность энтропии (СИ): . Энтропия зависит от массы тела и в ходе процесса она суммируется (аддитивная величина), т.е. обладает экстенсивными свойствами.
Согласно второму закону термодинамики изменение энтропии в квазистатическом (равновесном) процессе
(2.1.1)
т.е. изменение энтропии происходит под действием энергии, передаваемой в виде теплоты и равно приведенной теплоте .
Следствием второго закона термодинамики являются соотношения
dQнеобр < dQобр (2.1.2)
dWнеобр < dWобр
Т.е. работа любого необратимого процесса всегда меньше работы обратимого процесса между теми же начальным и конечным состояниями системы. Поэтому работу в обратимых процессах называют максимальной работой
Wобр = Wmax (2.1.3)
Чем меньше работа по сравнению с максимальной, тем более необратим процесс. Процессы, которые происходят без совершения работы, являются полностью необратимыми.
Теплота в необратимом процессе также меньше, чем в обратимом.
Таким образом, для необратимых (нестатических) процессов
dS > (2.1.4)
Свойства энтропии.
1)Энтропия – функция состояния; она имеет ту же размерность, что и теплоемкость:
2) Энтропия– понятие вероятностное, поэтому и второй закон термодинамики имеет статистический характер, энтропия связана с термодинамической вероятностью в формуле Больцмана:
S = kℓnW, (2.1.5)
где k – постоянная Больцмана; k = 1,38 × 10-23 Дж/K;
w – термодинамическая вероятность – число микросостояний, при помощи которых реализуется данное макросостояние.
Уравнение Больцмана можно представить и в другом виде:
, (2.1.6)
где R – универсальная газовая постоянная; R = 8,31441 ;
NA – число Авогадро; NA = 6,02204 × 1023 моль – 1.
3) Энтропия – экстенсивное свойство системы, зависящее от количества вещества в системе
Увеличение массы в n раз во столько же раз увеличивает энтропию.
4) Энтропия зависит от агрегатного состояния вещества.
5) S– величина аддитивная
S = S1 + S2 + … Sn.
Вычисление энтропии:
Изменение энтропии в химической реакции равно разности между энтропией продуктов реакции и энтропией исходных веществ
(2.1.7)
Если проводить расчет энтропии в условиях, отличных от стандартных, то:
(2.1.8)
Объединив I и II начала термодинамики, получим фундаментальное уравнение термодинамики (уравнение Гиббса) для закрытых систем:
dU £ TdS – pdV –dW/ (2.1.9)
где W/’ – все виды работ, совершаемые системой.
Уравнение (9) для закрытых систем, не способных совершать полезную работу:
dU £ TdS – PdV (2.1.10)
Если считать, что вся сообщаемая системе энергия идет на приращение внутренней энергии и на работу, совершаемую системой, то фундаментальное уравнение для равновесных процессов примет вид:
dU = TdS –– dW/’ (2.1.11)
Уравнения (2.1.9 – 2.1.11) представляют собой различные варианты фундаментального уравнения термодинамики и позволяют связать изменение внутренней энергии системы с возможностью протекания равновесного и самопроизвольного процессов.
Изменение энтропии вычисляют по следующим уравнениям:
1. Изменение энтропии при нагревании n молей любого вещества от температуры Т1 до Т2 при P = const рассчитывается по формуле
. (III,2)
Если зависимость СР от температуры описывается выражением
Cp = a + bT + сT2,
то
, (III,3)
2. Изменение энтропии при фазовом переходе рассчитывается по формуле
, (III,4)
где ΔН – теплота фазового перехода одного моля вещества; Т – абсолютная температура фазового перехода.
3. Изменение энтропии при переходе n молей идеального газа из одного состояния в другое вычисляется по уравнениям:
, (III,5)
или
,
, (III,6)
или
,
, (III,7)
где V1, P1, T1 и V2, P2, T2 – объем, давление, температура, характеризующие начальное и конечное состояние идеального газа соответственно; СР и СV – соответственно истинные мольные теплоемкости идеального газа при постоянных давлении и объеме: .
4. Изменение энтропии в процессе диффузии при смешении газов (при Р = const и Т = const), т.е. в изотермно-изобарном процессе, вычисляются по уравнению
(III,8)
или
, (III,9)
где n1, n2 – число молей первого и второго газа; N1 и N2 – мольные доли обоих газов; V1 и V2 – начальные объемы обоих газов; V – конечный объем смеси газов (V = V1 + V2).
5. Вычисление изменения энтропии по электрохимическим данным по уравнению
, (III,10)
где Н – тепловой эффект химической реакции; F – число Фарадея; Е – электродвижущая сила (э.д.с.) электрохимического момента, в котором протекает данная реакция; z – число электронов, участвующих в элементарном акте электродной реакции.
Второй закон термодинамики имеет статистический характер. Он характеризует переход системы из менее вероятного состояния к более вероятному. Это следует из статистического характера энтропии, которая связана с термодинамической вероятностью системы уравнением Больцмана:
S = klnw
Энтропия, понятие, впервые введенное в термодинамике для определения меры необратимого рассеяния энергии. Свойства энтропии: 1. Энтропия изолированной системы при протекании необратимого процесса возрастает. Действительно, изолированная (т. е. предоставленная самой себе) система переходит из менее вероятных в более вероятные состояния, что сопровождается ростом величины S. 2. Энтропия системы, находящейся в равновесном состоянии, максимальна. Энтропия системы, находящейся в равновесном состоянии, претерпевает незначительные кратковременные отрицательные флуктуации. Однако эти флуктуации столь малы, что практически энтропию можно считать постоянной и равной максимальному значению. Утверждение о том, что энтропия изолированной системы может только возрастать (либо по достижении максимального значения оставаться неизменной), носит название закона возрастания энтропии или второго начала термодинамики. Иначе можно сказать, что энтропия изолированной системы не может убывать. Итак, при протекании в изолированной системе необратимого процесса энтропия возрастает, т. е. выполняется соотношение dS > 0. Второе начало термодинамики можно сформулировать какзакон возрастания энтропии замкнутой системы при необратимых процессах: любой необратимый процесс в замкнутой системе происходит так, что энтропия системы при этом возрастает. Можно дать более краткую формулировку второго начала термодинамики: в процессах, происходящих в замкнутой системе, энтропия не убывает. Второе начало термодинамики в аксиоматической формулировке Рудольфа Юлиуса Клаузиуса (1865): Для любой квазиравновесной термодинамической системы существует однозначная функция термодинамического состояния , называемая энтропией, такая, что ее полный дифференциал . Вероятностное толкование понятия энтропии было дано в статистической физике Людвигом Больцманом. Для этого было введено понятие термодинамической вероятности (W) данного состояния некоторой системы. Термодинамическая вероятность означает число возможных неотличимых микроскопических состояний системы реализующих определенное макроскопическое состояние этой системы. В 1877 году Людвиг Больцман нашёл, что энтропия системы может относиться к количеству возможных «микросостояний» (микроскопических состояний), согласующихся с их термодинамическими свойствами. Рассмотрим, например, идеальный газ в сосуде. Микросостояние определено как позиции и импульсы (моменты движения) каждого составляющего систему атома. Связность предъявляет к нам требования рассматривать только те микросостояния, для которых: (I) месторасположения всех частей расположены в рамках сосуда, (II) для получения общей энергии газа кинетические энергии атомов суммируются. Больцман постулировал, что: S=k*ln(P) где константу k=1,38•10–23 Дж/К мы знаем теперь как постоянную Больцмана, а Ω является числом микросостояний, которые возможны в имеющемся макроскопическом состоянии (статистический вес состояния). Этот постулат, известный как принцип Больцмана, может быть оценен как начало статистической механики, которая описывает термодинамические системы, используя статистическое поведение составляющих их компонентов. Принцип Больцмана связывает микроскопические свойства системы (Ω) с одним из её термодинамических свойств (S). Согласно определению Больцмана, энтропия является просто функцией состояния. Так как Ω может быть только натуральным числом (1,2,3,…), то энтропия Больцмана должна быть положительной — исходя из свойств логарифма. В статистической термодинамике энтропия не только функция состояния системы и физическая величина, характеризующая направленность процессов в природе, но и мера беспорядка и хаоса. В изолированных системах все реальные процессы (например, расширение газа, диффузия, теплопередача) протекают в сторону увеличения энтропии. В результате этих процессов система приходит в состояние термодинамического равновесия, и ее макроскопические параметры (V, P, T) перестают меняться. В этом состоянии энтропия системы достигает максимального значения. Поэтому состояние термодинамического равновесия изолированной системы можно определить, как состояние с максимальным значением энтропии, или с максимальной величиной хаоса.
47. Явления переноса. Теплопроводность, диффузия, внутреннее трение в газах. Уравнения, описывающие эти явления. Коэффициенты переноса.
В термодинамически неравновесных системах происходят особые необратимые процессы, называемые явлениями переноса, в результате которых осуществляется пространственный перенос массы, импульса, энергии. К явлениям переноса относятся теплопроводность (перенос энергии), диффузия (перенос массы) и внутреннее трение (перенос импульса). Ограничимся одномерными явлениями переноса. Систему отсчета будем выберать так, чтобы ось х была направлена в сторону в направления переноса.
1. Теплопроводность. Если в первой области газа средняя кинетическая энергия молекул больше, чем во второй, то вследствие постоянных столкновений молекул с течением времени происходит процесс выравнивания средних кинетических энергий молекул, т. е., выравнивание температур. Перенос энергии в форме теплоты подчиняется закону Фурье: (1) где jE — плотность теплового потока — величина, которая определяется энергией, переносимой в форме теплоты в единицу времени через единичную площадку, перпендикулярную оси х, λ — теплопроводность, — градиент температуры, равный скорости изменения температуры на единицу длины х в направлении нормали к этой площадке. Знак минус говорит о том, что во время теплопроводности энергия перемещается в направлении убывания температуры (поэтому знаки jE и – противоположны). Теплопроводность λ равна плотности теплового потока при градиенте температуры, равном единице.
Можно показать, что (2) где сV — удельная теплоемкость газа при постоянном объеме (количество теплоты, которое необходимо для нагревания 1 кг газа на 1 К при постоянном объеме), ρ — плотность газа, <ν> — средняя скорость теплового движения молекул, <l> — средняя длина свободного пробега.
2. Диффузия. При происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и даже твердых тел; диффузия есть обмен масс частиц этих тел, при этом явление возникает и продолжается, пока существует градиент плотности. Во времена становления молекулярно-кинетической теории по вопросу явления диффузии возникли противоречия. Поскольку молекулы перемещаются в пространстве с огромными скоростями, то диффузия должна происходить очень быстро. Если же открыть в комнате крышку сосуда с пахучим веществом, то запах распространяется довольно медленно. Но здесь нет противоречия. При атмосферном давлении молекулы обладают малой длиной свободного пробега и, при столкновениях с другими молекулами, приемущественно «стоят» на месте. Явление диффузии для химически однородного газа подчиняется закону Фика: (3) где jm — плотность потока массы — величина, определяемая массой вещества, диффундирующего в единицу времени через единичную площадку, перпендикулярную оси х, D — диффузия (коэффициент диффузии), dρ/dx — градиент плотности, который равен скорости изменения плотности на единицу длины х в направлении нормали к этой площадке. Знак минус говорит о том, что перенос массы происходит в направлении убывания плотности (поэтому знаки jm и dρ/dx противоположны). Диффузия D численно равна плотности потока массы при градиенте плотности, равном единице. Согласно кинетической теории газов, (4)
3. Внутреннее трение (вязкость). Суть механизма возникновения внутреннего трения между параллельными слоями газа (жидкости), которые движущутся с различными скоростями, есть в том, что из-за хаотического теплового движения осуществляется обмен молекулами между слоями, в результате чего импульс слоя, который движется быстрее, уменьшается, который движется медленнее — увеличивается, что приводит к торможению слоя, который движется быстрее, и ускорению слоя, который движется медленнее. Как известно, сила внутреннего трения между двумя слоями газа (жидкости) подчиняется закону Ньютона: (5) где η — динамическая вязкость (вязкость), dν/dx — градиент скорости, который показывает быстроту изменения скорости в направлении х, перпендикулярном направлению движения слоев, S — площадь, на которую действует сила F.
Динамическая вязкость η численно равна плотности потока импульса при градиенте скорости, равном единице; она вычисляется по формуле (7)
Энтропия —
степень неопределенности состояния
системы.
Пример:
Пусть имеется два
дискретных ансамбя
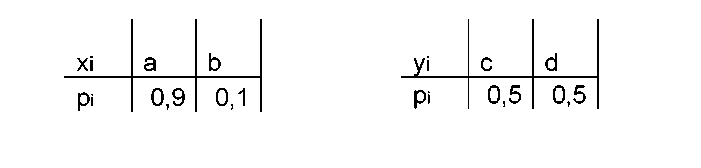
В дискретном
ансамбле у степень неопределенности
будет больше.
Собственная
информация сообщения х характеризует
информативность или степень
неожиданности конкретного ансамбля.
Математическое
ожидание этой величины будет
характеризовать информативность
всего ансамбля.
Определение:Энтропией
дискретного ансамбля X={xi,p(xi)}
называется
величина:
Н(х)
= M[I(x)]
= ∑I(xi)*p(xi)
=-∑P(Xi)
*logp(xi)
По определению
получается, что энтропия представляет
собой среднеожидаемое количество
информации от системы.
Свойства энтропии:
1) Неотрицательность
Н(х)>0
Энтропия будет
равной нулю, если система детерминированная
2) H(x)<log|x|
Равенство будет
иметь место, когда сообщение системы
равновероятно.
Пусть имеется
дискретный ансамбль X
и пусть на множестве его элементов
определена некоторая функция q(x),
введем дискретный ансамбль Y
= {y=q(x)},
тогда для множества Y
будет
выполняться неравенство H(Y)<H(X).
Это означает, что
обработка информации
не приводит к увеличению энтропии.
Условная энтропия
Пусть имеются две
зависимые системы X
и Y
. Обозначим p(yj/xi)
вероятность того, что система Y
примет значение Yj
при условии, что система X
приняло значение Xi
P(yj/xi)
= P(Y=yj,
при X=Xi).
Условные вероятности
должны быть заданы для всех значений
Y
и X.
Для их задания используется матрица
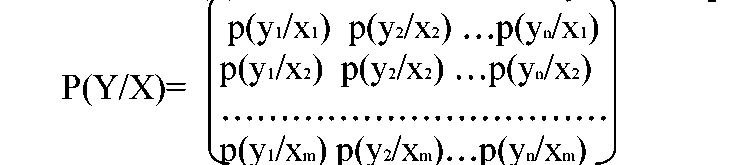
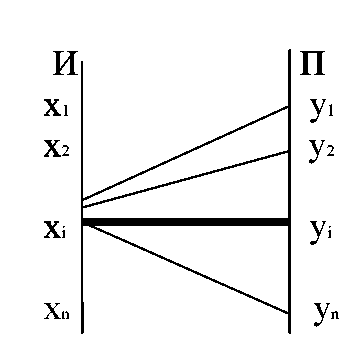
С помощью матрицы
можно посчитать частную энтропию:
H(Y/Xi)=∑p(yj/xi)
*logр(yj/xi)
Частную условную
энтропию можно выразить через
математическое ожидание H(Y/xi)
= M[-logp(Y/xi)].
Чтобы полностью
охарактеризовать энтропию системы
нужно определить полную или среднюю
энтропию. Для этого надо частную условную
энтропию усреднить по всем значениям
х с учетом вероятности.
Определение:
Полная условная
энтропия сообщения у относительно
х будет величина:

Понятие условной
энтропии используется для определения
информационных потерь, при передаче по
каналам связи с помехами. В этом случаи
система X
соответствует сообщениям источника,
система Y
— сигналы, принимаемые приемником.
Матрица P(Y/X)
характеризует информационные потери,
при передаче сообщений х.
—
p(yi/xi)
эта
вероятность соответствует правильному
приему
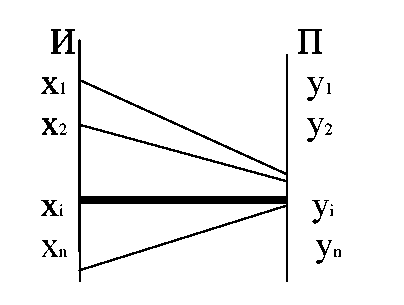
Таким образом,
H(Y/xi)
характеризует неопределенность того,
что, отправив Xi,
мы получим любой из элементов множества
Y.
Матрица, задающая
p(y/xi)
называется канальной матрицей.
Рассмотрим приемник,
т.е. систему Y.
Когда приемник получает сигнал у,
существует неопределенность: какой
сигнал был отправлен с источника.
В этом случае для
подсчета энтропии используется канальная
матрица P(X/Y).
Ей соответствует частная условная
энтропия Н(Х/уi)
и полная условная энтропия H(X/Y).
Энтропия сложной
системы. Объединение двух систем
X
и Y
называется сложная система X
и Y,
постоянные которой представляют
собой все возможные комбинации состоящих
X
и Y.
Если система
X={xi,p(xi)},
а система Y={yj,p(yj)},тогда
вероятности объединенной системы
(х,у) будем обозначать pij=p(xi,yj).
Эти вероятности удобно записывать в
виде матрицы P(X,Y).
Эта матрица обладает
следующими свойствами:
∑ pij=1
pi=∑pij
задают
распределение состояния системы X.
pj=∑pij
задают распределения системы Y.
Энтропией сложной
системы называется величина:
H(X,Y)=
— ∑∑
pij*log
pij
В
форме
математического
ожидания:
H(X,Y)
= M[-logp(xi,yj)]
Свойства энтропии
сложной системы:
1)Если
системы X
и Y
независимы, тогда
H(X,Y)=H(X)+H(Y)
2)Если
X
и Y
независимые системы, тогда
H(X,Y)=H(X)+H(Y/X)
Из
свойства 2 вытекает следствие:
H(X,Y)=H(Y)+H(X/Y)
H(X/Y)≤H(X)
и
H(Y/X)≤H(Y)H(X,Y)≤H(X)+H(Y)
5)Если системы
X
и Y
эквивалентны, то H(X,Y)=H(X)=H(Y).
Системы X
и Y
эквивалентны, если постоянные
одной системы полностью определяют
состояние другой системы.
Вывод:
Энтропия
характеризует среднеожидаемое количество
информации от системы.Если имеются две
взаимозависимые системы, то формула
энтропии по определению позволяет
вычислить энтропию источника
или энтропию приемника.Условная энтропия
H(X/Y)
определяет количество недостающей
информации на приемном конце.Энтропия
характеризует среднее количество
информации,
передаваемое по каналу связи с помехами.
