Какие свойства синус косинус
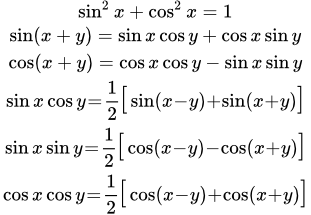
Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.
Содержание
Геометрическое определение синуса и косинусаПринятые обозначенияГрафики функций синус, y = sin x, и косинус, y = cos xСвойства синуса и косинусаПериодичностьЧетностьОбласть определения и значений, экстремумы, возрастание, убываниеОсновные формулыСумма квадратов синуса и косинусаФормулы синуса и косинуса от суммы и разностиФормулы произведения синусов и косинусовФормулы суммы и разностиВыражение синуса через косинусВыражение косинуса через синусВыражение через тангенсТаблица синусов и косинусов, тангенсов и котангенсовВыражения через комплексные переменныеФормула ЭйлераВыражения через гиперболические функцииПроизводныеИнтегралыРазложения в рядыСеканс, косекансОбратные функцииАрксинус, arcsinАрккосинус, arccosСм. также: Тангенс, котангенс, свойства, графики, формулы
Обратные тригонометрические функции, их графики и формулы
Геометрическое определение синуса и косинуса
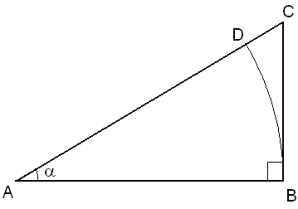Прямоугольный треугольник.
|BD| — длина дуги окружности с центром в точке A.
α — угол, выраженный в радианах.
Синус (sin α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos α) – это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
Графики функций синус, y = sin x, и косинус, y = cos x
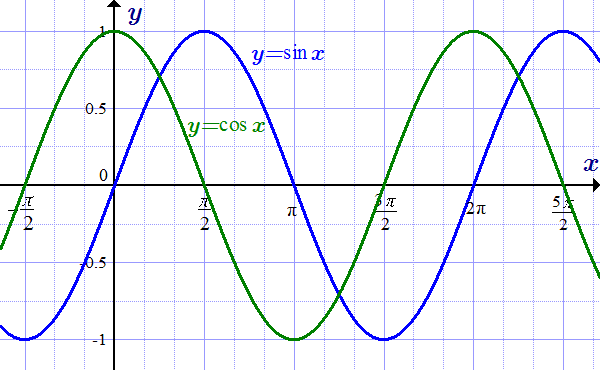Графики функций y=sin(x) и y=cos(x).
Графики синуса и косинуса смещены по оси x друг относительно друга на :
.
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2π.
Четность
Функция синус – нечетная. Функция косинус – четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Область значений | –1 ≤ y ≤ 1 | –1 ≤ y ≤ 1 |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = –1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
Далее мы полагаем, что – целое число.
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При , имеем:
; .
При :
; .
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента. 
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
; .
Интегралы
;
См. также раздел Таблица неопределенных интегралов >>>
Разложения в ряды
{ –∞ < x < +∞ }
{ –∞ < x < +∞ }
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: 15-02-2014 Изменено: 10-05-2020
См. также: Тангенс, котангенс, свойства, графики, формулы
Обратные тригонометрические функции, их графики и формулы
В этой статье будут рассмотрены три основных свойства тригонометрических функций: синуса, косинуса, тангенса и котангенса.
Первое свойство — знак функции в зависимости от того, какой четверти единичной окружности приналдежит угол α. Второе свойство — периодичность. Согласно этому свойству, тигонометрическая функция не меняет значения при изменении угла на целое число оборотов. Третье свойсто определяет, как меняются значения функций sin, cos, tg, ctg при противоположных углах α и -α.
Знаки тригонометрических функций по четвертям
Часто в математическом тексте или в контексте задачи можно встретить фразу: «угол первой, второй, третьей или четвертой координатной четверти». Что это такое?
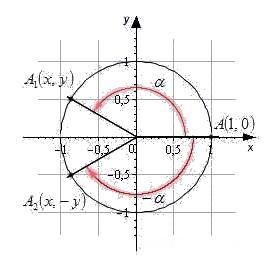
Обратимся к единичной окружности. Она разделена на четыре четверти. Отметим на окружности начальную точку A0(1, 0) и, поворачивая ее вокруг точки O на угол α, попадем в точку A1(x, y). В зависимости от того, в какой четверти будет лежать точка A1(x, y), угол α будет называться углом первой, второй, третьей и четвертой четвети соответственно.
Для наглядности приведем иллюстрацию.
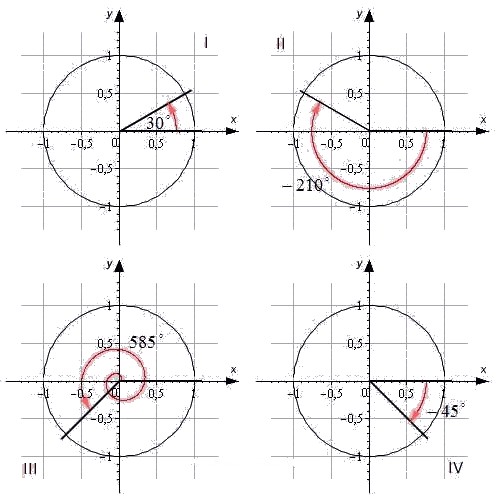
Угол α=30° лежит в первой четверти. Угол -210° является углом второй четверти. Угол 585° — угол третьей четверти. Угол -45° — это угол четвертой четверти.
При этом углы ±90°, ±180°, ±270°, ±360° не принадлежат ни одной четверти, так как лежат на координатных осях.
Теперь рассмотрим знаки, которые принимают синус, косинус, тангенс и котангенс в зависимости от того, в какой четверти лежит угол.
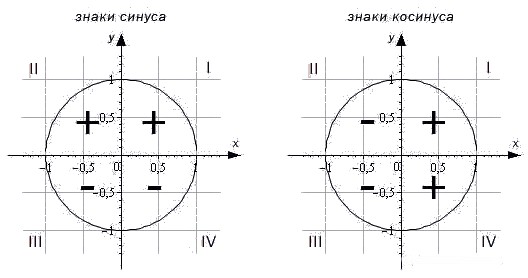
Чтобы определить знаки синуса по четвертям, вспомним опредение. Синус — это ордината точки A1(x, y). Из рисунка видно, что в первой и второй четвертях она положительна, а в третьей и четверной — отрицательна.
Косинус — это абсцисса точки A1(x, y). В соответсии с этим, определяем знаки косинуса на окружности. Косинус положителен в первой и четвертой четвертях, а отрицателен во второй и третьей четверти.
Для определения знаков тангенса и котангенса по четвертям также вспоминаем определения этих тригонометрических функций. Тангенс — отношение ординаты точки к абсциссе. Значит, по правилу деления чисел с разными знаками, когда ордината и абсцисса имеют одинаковые знаки, знак тангенса на окружности будет положительным, а когда ордината и абсцисса имеют разные знаки — отрицательным. Аналогично определяются знаки котангенса по четвертям.
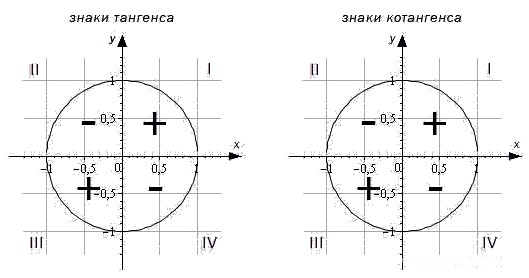
Важно помнить!
- Синус угла α имеет знак плюс в 1 и 2 четвертях, знак минус — в 3 и 4 четвертях.
- Косинус угла α имеет знак плюс в 1 и 4 четвертях, знак минус — в 2 и 3 четвертях.
- Тангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
- Котангенс угла α имеет знак плюс в 1 и 3 четвертях, знак минус — в 2 и 4 четвертях.
Свойство периодичности
Свойство периодичности — одно из самых очевидных свойств тригонометрических функций.
Свойство периодичности
При изменении угла на целое число полных оборотов значения синуса, косинуса, тангенса и котангенса данного угла остаются неизменными.
Действительно, при изменении угла на целое число оборотов мы всегда будем попадать из начальной точки A на единичной окружности в точку A1 с одними и теми же координатами. Соответственно, не будут меняться и значения синуса, косинуса, тангенса и котангенса.
Математически данное свойство записывается так:
sinα+2π·z=sin αcosα+2π·z=cos αtgα+2π·z=tg αctgα+2π·z=ctg α
Какое применение на практике находит это свойство? Свойство периодичности, как и формулы приведения, часто используется для вычисления значений синусов, косинусов, тангенсов и котангенсов больших углов.
Приведем примеры.
sin13π5=sin3π5+2π=sin3π5
tg(-689°)=tg(31°+360°·(-2))=tg31°tg(-689°)=tg(-329°+360°·(-1))=tg(-329°)
Свойства синусов, косинусов, тангенсов и котангенсов противоположных углов
Вновь обратимся к единичной окружности.
Точка A1(x, y) — результат поворота начальной точки A0(1, 0) вокруг центра окружности на угол α. Точка A2(x, -y) — результат поворота начальной точки на угол -α.
Точки A1и A2 симметричны относительно оси абсцисс. В случае, когда α=0°, ±180°, ±360° точки A1и A2 совпадают. Пусть одна точка имеет координаты (x, y), а вторая — (x, -y). Вспомним определения синуса, косинуса, тангенса, котангенса и запишем:
sin α=y, cos α=x, tg α=yx, ctg α=xysin-α=-y, cos-α=x, tg-α=-yx, ctg-α=x-y
Отсюда следует свойство синусов, косинусов, тангенсов и котангенсов противоположных углов.
Свойство синусов, косинусов, тангенсов и котангенсов противоположных углов
sin-α=-sin αcos-α=cos αtg-α=-tg αctg-α=-ctg α
Согласно этому свойству, справедливы равенства
sin-48°=-sin 48°, ctgπ9=-ctg-π9, cos 18°=cos-18°
Рассмотренное свойство часто используется при решении практических задач в случаях, когда нужно избавиться от отрицательных знаков углов в агрументах тригонометрических функций.
Запрос «sin» перенаправляется сюда; см. также другие значения.
Запрос «sec» перенаправляется сюда; см. также другие значения.
Запрос «Синус» перенаправляется сюда; см. также другие значения.
Рис. 1.
Графики тригонометрических функций: синуса, косинуса, тангенса, котангенса, секанса, косеканса
Тригонометри́ческие фу́нкции — элементарные функции[1], которые исторически возникли при рассмотрении прямоугольных треугольников и выражали зависимости длин сторон этих треугольников от острых углов при гипотенузе (или, что равнозначно, зависимость хорд и высот от центрального угла дуги в круге). Эти функции нашли широкое применение в самых разных областях науки. По мере развития математики определение тригонометрических функций было расширено, в современном понимании их аргументом может быть произвольное вещественное или комплексное число.
Раздел математики, изучающий свойства тригонометрических функций, называется тригонометрией.
К тригонометрическим функциям традиционно причисляют:
прямые тригонометрические функции:производные тригонометрические функции:другие тригонометрические функции:обратные тригонометрические функции:
- арксинус, арккосинус и т. д.
В типографике литературы на разных языках сокращённое обозначение тригонометрических функций различно, например, в англоязычной литературе тангенс, котангенс и косеканс обозначаются , , . До Второй мировой войны в Германии и во Франции эти функции обозначались так же, как принято в русскоязычных текстах[2], но потом в литературе на языках этих стран был принят англоязычный вариант записи тригонометрических функций.
Кроме этих шести широко известных тригонометрических функций, иногда в литературе используются некоторые редко используемые тригонометрические функции (версинус и т. д.).
Синус и косинус вещественного аргумента представляют собой периодические, непрерывные и бесконечно дифференцируемые вещественнозначные функции. Остальные четыре функции на вещественной оси также вещественнозначны, периодичны и бесконечно дифференцируемы, за исключением счётного числа разрывов второго рода: у тангенса и секанса в точках , а у котангенса и косеканса — в точках .
Графики тригонометрических функций показаны на рис. 1.
Способы определения[править | править код]
Определение для любых углов[править | править код]
Рис. 2.
Определение тригонометрических функций
Обычно тригонометрические функции определяются геометрически[3]. Пусть нам дана декартова система координат на плоскости, и построена окружность радиуса с центром в начале координат . Всякий угол можно рассматривать как поворот от положительного направления оси абсцисс до некоторого луча , при этом направление поворота против часовой стрелки считается положительным, а по часовой стрелке — отрицательным. Абсциссу точки обозначим , ординату обозначим (см. рисунок 2).
В силу свойств подобных фигур значения тригонометрических функций не зависят от величины радиуса окружности . Часто радиус принимают равным величине единичного отрезка; тогда синус равен ординате , а косинус — абсциссе . На рисунке 3 показаны величины тригонометрических функций для единичной окружности.
Если — вещественное число, то синусом в математическом анализе называется синус угла, радианная мера которого равна . Аналогично для прочих тригонометрических функций.
Определение для острых углов[править | править код]
Рис. 4.
Тригонометрические функции острого угла
В школьном курсе геометрии тригонометрические функции
острого угла определяются как отношения сторон прямоугольного треугольника[4]. Пусть OAB — прямоугольный треугольник с острым углом α. Тогда:
Построив систему координат с началом в точке , направлением оси абсцисс вдоль и в случае необходимости изменив ориентацию (перевернув) треугольник так, чтобы он находился в первой четверти системы координат, и затем, построив окружность с радиусом, равным гипотенузе, сразу находим, что такое определение функций приводит к тому же результату, что и предыдущее.
Данное определение имеет некоторое методическое преимущество, так как не требует введения понятия системы координат, но также и такой крупный недостаток, что невозможно определить тригонометрические функции даже для тупых углов, которые необходимо знать при решении элементарных задач о тупоугольных треугольниках. (См.: теорема синусов, теорема косинусов).
Тригонометрические функции являются периодическими функциями с периодами (360°) для синуса, косинуса, секанса и косеканса, и (180°) для тангенса и котангенса.
Тригонометрические функции любого угла можно свести к тригонометрическим функциям острого угла, используя их периодичность и так называемые формулы приведения.
Это необходимо, например, для нахождения значений тригонометрических функций по таблицам, поскольку в таблицах обычно приводятся значения только для острых углов.
Определение как решений дифференциальных уравнений[править | править код]
Функции косинус и синус можно определить как чётное (косинус) и нечётное (синус) решения дифференциального уравнения
с дополнительными условиями:
для косинуса и для синуса, то есть как функций одной переменной, вторая производная которых равна самой функции, взятой со знаком минус:
Определение как решений функциональных уравнений[править | править код]
Функции косинус и синус можно определить[5]
как решения ( и соответственно) системы функциональных уравнений:
при дополнительных условиях:
и при .
Определение через ряды[править | править код]
Используя геометрию и свойства пределов, можно доказать, что производная синуса равна косинусу, и что производная косинуса равна минус синусу. Тогда можно воспользоваться теорией рядов Тейлора и представить синус и косинус в виде степенны́х рядов:
Пользуясь этими формулами, а также равенствами и можно найти разложения в ряд и других тригонометрических функций:
где
— числа Бернулли,
— числа Эйлера.
Значения тригонометрических функций для некоторых углов[править | править код]
Значения синуса, косинуса, тангенса, котангенса, секанса и косеканса для некоторых углов приведены в таблице. («∞» означает, что функция в указанной точке не определена, а в её окрестности стремится к бесконечности).
Значения косинуса и синуса на окружности
Значения тригонометрических функций нестандартных углов[править | править код]
Значения тригонометрических функций для некоторых других углов
Свойства тригонометрических функций[править | править код]
Простейшие тождества[править | править код]
Поскольку синус и косинус являются соответственно ординатой и абсциссой точки, соответствующей на единичной окружности углу α, то, согласно уравнению единичной окружности или теореме Пифагора, имеем:
Это соотношение называется основным тригонометрическим тождеством.
Деля это уравнение на квадрат косинуса и синуса соответственно, имеем далее:
Из определения тангенса и котангенса следует, что
Любую тригонометрическую функцию можно выразить через любую другую тригонометрическую функцию с тем же аргументом[6]:
Непрерывность[править | править код]
- Синус и косинус — непрерывные функции.
- Тангенс и секанс имеют точки разрыва ±π/2, ±3π/2, ±5π/2, …, ±(n + 1/2)π, … (в градусной мере: ±90°, ±270°, ±450°, …, ±(n + 1/2)·180°, …).
- Котангенс и косеканс имеют точки разрыва 0, ±π, ±2π, …, ±nπ, … (в градусной мере: 0°, ±180°, ±360°, …, ±n·180°, …).
Чётность[править | править код]
Косинус и секанс — чётные. Остальные четыре функции — нечётные, то есть:
Периодичность[править | править код]
Функции — периодические с периодом , функции и — c периодом .
Формулы приведения[править | править код]
Формулами приведения называются формулы следующего вида:
Здесь — любая тригонометрическая функция, — соответствующая ей кофункция (то есть косинус для синуса, синус для косинуса, тангенс для котангенса, котангенс для тангенса, секанс для косеканса и косеканс для секанса), n — целое число. Перед полученной функцией ставится тот знак, который имеет исходная функция в заданной координатной четверти при условии, что угол α острый, например:
или что то же самое:
Некоторые формулы приведения:
Формулы сложения[править | править код]
Значения тригонометрических функций суммы и разности двух углов:
Аналогичные формулы для суммы трёх углов:
Формулы для кратных углов[править | править код]
Формулы двойного угла:
Формулы тройного угла:
Прочие формулы для кратных углов:
следует из формулы дополнения и формулы Гаусса для гамма-функции.
Из формулы Муавра можно получить следующие общие выражения для кратных углов:
где — целая часть числа , — биномиальный коэффициент.
Формулы половинного угла:
Произведения[править | править код]
Формулы для произведений функций двух углов:
Аналогичные формулы для произведений синусов и косинусов трёх углов:
Формулы для произведений тангенсов и котангенсов трёх углов можно получить, поделив правые и левые части соответствующих равенств, представленных выше.
Степени[править | править код]
Иллюстрация равенства
Суммы[править | править код]
Существует представление:
где угол находится из соотношений:
Универсальная тригонометрическая подстановка[править | править код]
Все тригонометрические функции можно выразить через тангенс половинного угла:
Исследование функций в математическом анализе[править | править код]
Разложение в бесконечные произведения[править | править код]
Тригонометрические функции могут быть представлены в виде бесконечного произведения многочленов:
Эти соотношения выполняются при любом значении .
Цепные дроби[править | править код]
Производные и первообразные[править | править код]
Все тригонометрические функции непрерывно и неограниченно дифференцируемы на всей области определения:
Интегралы тригонометрических функций на области определения выражаются через элементарные функции следующим образом[7]:
Тригонометрические функции комплексного аргумента[править | править код]
Определение[править | править код]
Формула Эйлера:
Формула Эйлера позволяет определить тригонометрические функции от комплексных аргументов через экспоненту или (с помощью рядов) как аналитическое продолжение их вещественных аналогов:
где
Соответственно, для вещественного x:
Комплексные синус и косинус тесно связаны с гиперболическими функциями:
Большинство перечисленных выше свойств тригонометрических функций сохраняются и в комплексном случае. Некоторые дополнительные свойства:
- комплексные синус и косинус, в отличие от вещественных, могут принимать сколь угодно большие по модулю значения;
- все нули комплексных синуса и косинуса лежат на вещественной оси.
Комплексные графики[править | править код]
На следующих графиках изображена комплексная плоскость, а значения функций выделены цветом. Яркость отражает абсолютное значение (чёрный — ноль). Цвет изменяется от аргумента и угла согласно карте.
История названий[править | править код]
Линия синуса (линия AB на рис. 2) у индийских математиков первоначально называлась «арха-джива» («полутетива», то есть половина хорды данной дуги, поскольку дуга с хордой напоминает лук с тетивой). Затем слово «арха» было отброшено и линию синуса стали называть просто «джива». Арабские математики, переводя индийские книги с санскрита, не перевели слово «джива» арабским словом «ватар», обозначающим тетиву и хорду, а транскрибировали его арабскими буквами и стали называть линию синуса «джиба» (جيب). Так как в арабском языке краткие гласные не обозначаются, а долгое «и» в слове «джиба» обозначается так же, как полугласная «й», арабы стали произносить название линии синуса как «джайб», что буквально обозначает «впадина», «пазуха». При переводе арабских сочинений на латынь европейские переводчики перевели слово «джайб» латинским словом sinus — «синус», имеющим то же значение (именно в этом значении оно применяется как анатомический термин синус). Термин «косинус» (лат. cosinus) — это сокращение от лат. complementi sinus — дополнительный синус.
Современные краткие обозначения , введены Уильямом Отредом и Бонавентурой Кавальери и закреплены в трудах Леонарда Эйлера.
Термины «тангенс» (лат. tangens — касающийся) и «секанс» (лат. secans — секущий) были введены датским математиком Томасом Финке в его книге «Геометрия круглого» (Geometria rotundi, 1583).
Сам термин тригонометрические функции введён Клюгелем в 1770 году.
Позднее были введены и термины для обратных тригонометрических функций — арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс — с помощью добавления приставки «арк» (от лат. arcus — дуга), — Ж. Лагранжем и др.
См. также[править | править код]
- Гиперболические функции
- Интегральный синус
- Интегральный косинус
- Интегральный секанс
- Обратные тригонометрические функции
- Редко используемые тригонометрические функции
- Решение треугольников
- Синус-верзус
- Сферическая тригонометрия
- Тригонометрические тождества
- Тригонометрические функции от матрицы
- Тригонометрический ряд Фурье
- Функция Гудермана
- Четырёхзначные математические таблицы (Таблицы Брадиса)
- Эллиптические функции
Литература[править | править код]
- Бермант А. Ф., Люстерник Л. А. Тригонометрия. — М.: Наука, 1967.
- Тригонометрические функции — статья из Большой советской энциклопедии. — М.: Советская энциклопедия, 1977. — Т. 26. — С. 204—206.
- Бронштейн И. Н., Семендяев К. А. Прямолинейная тригонометрия // Справочник по математике. — Изд. 7-е, стереотипное. — М.: Государственное издательство технико-теоретической литературы, 1967. — С. 179—184.
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Переиздание: М.: АСТ, 2006. — 509 с. — ISBN 5-17-009554-6 www.alleng.ru/d/math/math42.htm
- Двайт Г. Б. Тригонометрические функции // Таблицы интегралов и другие математические формулы. — 4-е изд. — М.: Наука, 1973. — С. 70—102.
- Кожеуров П. А. Тригонометрия. — М.: Физматгиз, 1963.
- Маркушевич А. И. Замечательные синусы. — М.: Наука, 1974.
- Математическая энциклопедия / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1984. — И. М. Виноградов. Тригонометрические функции // Математическая энциклопедия. — М.: Советская энциклопедия (рус.). — 1977—1985.
- Тригонометрические функции // Энциклопедический словарь юного математика / Ред. коллегия, Гнеденко Б. В. (гл. ред.), Савин А. П. и др. — М.: Педагогика, 1985 (1989). — С. 299—301—305. — 352 с., ил. — ISBN 5-7155-0218-7 (С. 342, 343 — таблицы тригонометрических функций 0°-90°, в том числе в радианах)
- Тригонометрические функции // Справочник по математике (для ср. уч. заведений) / Цыпкин А. Г., под ред. Степанова С. А. — 3-е изд. — М.: Наука, Гл. редакция физ.-мат. литературы, 1983. — С. 240—258. — 480 с.
Ссылки[править | править код]
- GonioLab — прояснённая единичная окружность, тригонометрические и гиперболические функции (Java Web Start)
- Weisstein, Eric W. Trigonometric Functions (англ.) на сайте Wolfram MathWorld.
- Онлайн калькулятор: вычисление значений тригонометрических функций (в том числе нахождение углов треугольника по сторонам)
- Интерактивная карта значений тригонометрических функций
- Тригонометрические таблицы (0° — 360°)
- «Синус и косинус — это проценты» — перевод статьи How To Learn Trigonometry Intuitively | BetterExplained (англ.)
Примечания[править | править код]
- ↑ Справочник: Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров). — М.: Наука, 1973. — 720 с. относит их к специальным функциям.
- ↑ Знак математический. // Большая советская энциклопедия. 1-е изд. Т. 27. — М., 1933.
- ↑ Справочник по элементарной математике, 1978, с. 282—284.
- ↑ Справочник по элементарной математике, 1978, с. 271—272.
- ↑ Ильин В. А., Позняк Э. Г. Основы математического анализа. Ч. 1. — М.: Наука, 1998. — ISBN 5-02-015231-5.
- ↑ Для значений аргумента, для которых нижеприведённые формулы определены.
- ↑ В формулах, содержащих логарифм в правой части равенств, константы интегрирования , вообще говоря, различны для различных интервалов непрерывности.