Какие свойства параллельного переноса

Параллельный перенос
Теперь рассмотрим, какие бывают виды движения. Будем использовать нашу аналогию с бесконечным листом бумаги. Одно из возможных движений – передвинуть его вдоль плоскости. В этом случае все точки сдвинутся на один и тот же вектор.
Действительно, передвинем произвольный треугольник. Если соединять прообразы с их образами, то получим равные векторы перемещения. Т. к. все они параллельны друг другу, то такое перемещение называют параллельным переносом. Дадим ему формальное определение.
Пусть задан вектор . Параллельный перенос – это такое отображение плоскости на себя, при котором каждая точка плоскости отображается в точку таким образом, что
(см. рис. 13). Проще говоря, параллельный перенос – это такое отображение, при котором каждая точка перемещается на вектор . Чтобы задать параллельный перенос, нужно задать этот вектор .
Рис. 13. Параллельный перенос
Является ли параллельный перенос движением? В нашем представлении, конечно, да. Но докажем этот факт формально. Чтобы это сделать, нужно показать, что параллельный перенос сохраняет расстояние между точками.
Теорема 2. Параллельный перенос сохраняет расстояние между точками.
Доказательство
Пусть задано движение вектором . Рассмотрим произвольные точки и . Их образами являются точки и (см. рис. 14).
Рис. 14. Движение задано вектором , точки и – образы и
По определению параллельного переноса:
Значит, в четырехугольнике две противоположные стороны равны и параллельны:
Но тогда это параллелограмм (ответьте, почему). А значит, и другие две противоположные стороны равны друг другу:
Т. е. расстояние между прообразами и расстояние между образами равны.
Мы показали, что параллельный перенос сохраняет расстояние, а следовательно, является движением.
Доказано.
Поворот
Еще один вариант движения – повернуть лист бумаги. Понятно, что одна из точек при этом окажется неподвижной (центр поворота). Это уже говорит о том, что поворот не является параллельным переносом (при параллельном переносе ни одна из точек не останется на месте). Дадим строгое определение поворота.
Выберем точку – центр поворота – и угол , на который будем поворачивать. Выберем теперь произвольную точку и повернем ее вокруг точки на угол . Для этого найдем ее образ такой, что , а угол (см. рис. 15).
Рис. 15. Поворот
Если для параллельного переноса нужно было задать вектор этого переноса, то, чтобы задать поворот, необходимо указать центр поворота и угол поворота .
Направление против часовой стрелки договорились считать положительным. Поэтому если речь идет о повороте на положительный угол , то поворачивать будем именно против часовой стрелки (см. рис. 16).
Рис. 16. Поворот против часовой стрелки:
Если необходим поворот по часовой стрелке, скажем на , то нужно указать угол поворот (см. рис. 17).
Рис. 17. Поворот по часовой стрелке:
Покажем, что при повороте сохраняются расстояния между точками, т. е. поворот является движением.
Теорема 3. При повороте сохраняются расстояния, т. е. поворот является движением.
Доказательство
Повернем точки и вокруг точки на угол . Получим их образы и (см. рис. 18).
Рис. 18. Точки и повернули вокруг точки на угол и получили их образы и
Надо доказать, что расстояние не изменилось, т. е.:
Для этого покажем, что равны треугольники и (см. рис. 19).
Рис. 19. Рассматриваемые треугольники и
В самом деле, углы при вершине у них равны как сумма общего угла и угла :
По определению поворота:
Тогда треугольники и равны по первому признаку равенства. Итак, поворот является движением, т. к. сохраняет расстояние между точками.
Доказано.
Осевая симметрия
Два рассмотренных движения (параллельный перенос и поворот) при их комбинировании задают практически любое движение, которое мы можем представить.
В самом деле, передвиньте книгу по столу так, как вам этого захочется. Движение книги можно разложить на два (см. рис. 20): параллельный перенос до того места, где она находится теперь, и поворот до того положения, в котором она оказалась. Можно сказать, что все движения можно описать параллельным переносом и поворотом.
Рис. 20. Разложение движения книги на два: параллельный перенос и поворот
Но с помощью такого движения мы никогда не сможем получить книгу, повернутую к нам другой стороной обложки – как бы мы ее ни переносили и ни поворачивали, ее ориентация в пространстве не изменится. И здесь нам на помощь придет симметрия, о которой мы говорили в начале урока. Вспомните: в зеркале правая рука становится левой.
Две точки и называются симметричными относительно прямой , если прямая проходит через середину отрезка перпендикулярно ему (см. рис. 21).
Рис. 21. Точки и , симметричные относительно прямой
Понятно, что для любой точки всегда существует симметричная точка и причем единственная. Зададим отображение, используя это понятие.
Осевой симметрией относительно прямой называется отображение плоскости на себя, при котором каждая точка плоскости переходит в точку, ей симметричную относительно прямой (см. рис. 22).
Рис. 22. Осевая симметрия
Нетрудно показать, что такое отображение сохраняет расстояние.
Теорема 4. При осевой симметрии сохраняются расстояния, т. е. осевая симметрия является движением.
Доказательство
Рассмотрим случай, когда оба прообраза (точки и ) лежат с одной стороны от оси симметрии (см. рис. 23).
Рис. 23. Точки и лежат с одной стороны от оси симметрии
Построим их образы, точки и , симметричные относительно прямой (см. рис. 24).
Рис. 24. Точки и – образы точек и
Необходимо доказать:
Сделать это можно, например, так: построим два прямоугольных треугольника и (см. рис. 25).
Рис. 25. Рассматриваемые прямоугольные треугольники и
Видим ли мы, что четырехугольник – прямоугольник? Да, видим.
Стороны и перпендикулярны одной прямой, а значит, параллельны друг другу:
Стороны и тоже перпендикулярны одной прямой, следовательно, тоже параллельны:
Четырехугольник уже параллелограмм, и у него уже есть два прямых угла. Он прямоугольник, тогда:
Вычтем из них равные отрезки и и получим:
Тогда в двух прямоугольных треугольниках и катеты попарно равны, что является признаком равенства треугольников. Раз треугольники равны, то равны их гипотенузы , т. е. расстояния между прообразами и образами. Осевая симметрия сохраняет расстояние и является движением.
Доказано.
Существуют, конечно, и другие варианты расположения прообразов относительно оси симметрии. Вот некоторые из них (см. рис. 26). Попробуйте самостоятельно доказать сохранение расстояний в этих случаях.
Рис. 26. Некоторые варианты расположения прообразов относительно оси симметрии
Легко убедиться, что осевая симметрия не сводится к параллельному переносу и повороту – именно симметричный себе образ мы видим в зеркале. Конечно, если «выйти» из плоскости и рассмотреть движение в пространстве, то осевую симметрию можно свести к переносу и повороту – при повороте в пространстве наша книга может поменять ориентацию. Но мы рассматриваем только преобразования плоскости, и в этом случае осевая симметрия – отдельный вид движения.
Если некая осевая симметрия переводит фигуру саму в себя, то ось симметрии называют осью симметрии фигуры.
У одной фигуры может быть одна, несколько или бесконечное количество осей симметрии. Например, у равнобедренного треугольника медиана, проведенная к основанию, является осью симметрии (см. рис. 27). У произвольного прямоугольника две оси симметрии. Посчитайте, сколько осей симметрии у равностороннего треугольника, параллелограмма, ромба, квадрата, круга.
Рис. 27. В равнобедренном треугольнике медиана, проведенная к основанию, является осью симметрии
Центральная симметрия
Последним движением, которое мы рассмотрим, является центральная симметрия. Центральная симметрия – это симметрия относительно выбранной точки, центра симметрии.
Зафиксируем точку – это будет центр симметрии. Выберем произвольную точку . Точка будет ее образом, если точка является серединой отрезка (см. рис. 28).
Рис. 28. Центральная симметрия
Доказательство того факта, что центральная симметрия является движением, т. е. сохраняет расстояния между точками, элементарно.
Теорема 5. При центральной симметрии сохраняются расстояния, т. е. центральная симметрия является движением.
Доказательство
Построим для двух прообразов и их образы и , т. е. точки, симметричные относительно центра симметрии (см. рис. 29).
Рис. 29. Точки и симметричны относительно центра симметрии точкам и
Полученные два треугольника и равны по первому признаку:
- углы (как вертикальные);
- стороны (по определению симметрии);
- стороны (по определению симметрии).
Следовательно, отрезки:
Т. е. расстояния при центральной симметрии сохраняются.
Доказано.
В данной статье мы будем рассматривать понятие параллельного переноса в трехмерном пространстве. Но вначале нам надо рассмотреть такие понятия как отображение и движение в пространстве.
Понятие движения
Перед тем, как ввести понятие движения в пространстве, надо ввести определение отображения пространства на себя.
Определение 1
Отображением пространства на себя будем называть такое соответствие любой точке данного пространства какой-либо точке этого же пространства, в котором участвуют все точки из этого пространства.
Введем теперь, непосредственно, определение движения.
Определение 2
Движением пространства будем называть отображением пространства на себя, которое сохраняется расстояния между соответствующими точками.
Пример – рисунок 1.
Введем теперь несколько теорем, связанных с понятием движения без доказательства.
Теорема 1
При движении отрезок будет отображаться на ему же равный отрезок.
Теорема 2
При движении треугольник будет отображаться на равный ему же треугольник.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Теорема 3
При движении пирамида будет отображаться на равную ей пирамиду.
Основными примерами движений в геометрии являются осевая симметрия, центральная симметрия, зеркальная симметрия, поворот и параллельный перенос. Доказательство того, что параллельный перенос действительно является движением, нами будет рассмотрено ниже.
Параллельный перенос
Введем теперь, непосредственно, понятие параллельного переноса на какой-либо вектор. Пусть нам дан вектор $overline{α}$.
Определение 3
Параллельным переносом на вектор $overline{α}$ будем называть такое отображение плоскости само на себя, при котором произвольная точка $M$ отображается на такую точку $M_1$, что выполняется равенство $overline{MM_1}=overline{α}$
(Рис. 2).
Введем следующую теорему, связанную с понятием параллельного переноса.
Теорема 4
Параллельный перенос — движение.
Доказательство.
Рассмотрим в пространстве две произвольные точки $M$ и $N$. Будем рассматривать параллельный перенос на данный нам вектор $overline{α}$. Пусть при нашем параллельном переносе данные нам точки отображаются, соответственно, в точки $M_1$ и $N_1$ (рис. 3).
Из определения 3 параллельного переноса получим, что $overline{MM_1}=overline{a}$, а $overline{NN_1 }=overline{a}$, следовательно, получим, что $overline{MM_1}=overline{NN_1}$.
Тогда, из определения равных векторов будем получать, что
$|MM_1|=|NN_1|$, $MM_1||NN_1$
Получаем, что четырехугольник $MM_1N_1N$ будет являться параллелограммом и, как следствие, верно равенство: $|MN|=|M_1N_1|$. Отсюда получаем, что параллельный перенос будет сохранять расстояния, что и доказывает нашу теорему.
Пример задачи
Пример 1
Постройте параллельный перенос куба на вектор $overline{h}$, изображенных на рисунке 4.
Решение.
Для построения параллельного переноса сначала проведем через все точки тетраэдра прямые, параллельные заданному нам вектору $overline{h}$ (рис. 5).
Далее, для построения будем использовать определение 3. Точка $X$ перейдет в такую точку $X_1$, которая будет принадлежать прямой $x$. Точка $Y$ перейдет в такую точку $Y_1$, которая будет принадлежать прямой $y$. Точка $Z$ перейдет в такую точку $Z_1$, которая будет принадлежать прямой $z$. Точка $O$ перейдет в такую точку $O_1$, которая будет принадлежать прямой $o$. Точка $X’$ перейдет в такую точку $X’_1$, которая будет принадлежать прямой $a$. Точка $Y’$ перейдет в такую точку $Y’_1$, которая будет принадлежать прямой $b$. Точка $Z’$ перейдет в такую точку $Z’_1$, которая будет принадлежать прямой $c$. Точка $O’$ перейдет в такую точку $O’_1$, которая будет принадлежать прямой $o’$. Причем будут выполняться равенства:
$overline{XX_1}=overline{h}$, $overline{YY_1}=overline{h}$, $overline{ZZ_1}=overline{h}$, $overline{OO_1}=overline{h}$, $overline{X’X’_1}=overline{h}$, $overline{Y’Y’_1}=overline{h}$, $overline{Z’Z’_1}=overline{h}$, $overline{O’O’_1}=overline{h}$
Отметим эти точки (рис. 6).
Соединив эти точки между собой, мы и получим искомый нами параллельный перенос на вектор $overline{h}$ (рис. 7).
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Движения
- Параллельный перенос
Если нам дан вектор  , то параллельным переносом на вектор
, то параллельным переносом на вектор  называется отображение плоскости на себя, при котором произвольная точка Е отображается в такую точку Е1, что
называется отображение плоскости на себя, при котором произвольная точка Е отображается в такую точку Е1, что 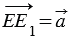 .
.
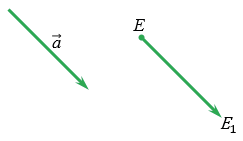
Доказательство:
Дано: точки Е и К отображаются в точки Е1 и К1 при параллельном переносе на  .
.
Доказать: параллельный перенос — движение.
Доказательство:
1 случай
Точки Е и К не лежат на одной прямой параллельной вектору  .
.
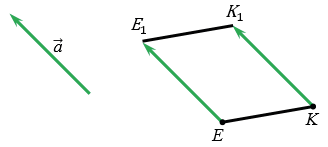
По условию точки Е и К отображаются в точки Е1 и К1 соответственно при параллельном переносе на вектор  , тогда по определению параллельного переноса
, тогда по определению параллельного переноса 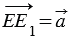 и
и 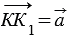 , поэтому
, поэтому  , следовательно,
, следовательно, 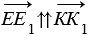 и
и 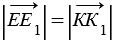 , значит, ЕЕ1
, значит, ЕЕ1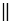 КК1 (т.к. точки Е и К не лежат на одной прямой параллельной вектору
КК1 (т.к. точки Е и К не лежат на одной прямой параллельной вектору  ) и ЕЕ1= КК1. Следовательно, по признаку параллелограмма четырехугольник ЕЕ1К1К — параллелограмм, поэтому по свойству параллелограмма ЕК = Е1К1, т.е. расстояние между точками Е и К равно расстоянию между точками Е1 и К1. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.
) и ЕЕ1= КК1. Следовательно, по признаку параллелограмма четырехугольник ЕЕ1К1К — параллелограмм, поэтому по свойству параллелограмма ЕК = Е1К1, т.е. расстояние между точками Е и К равно расстоянию между точками Е1 и К1. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.
2 случай
Точки Е и К лежат на одной прямой параллельной вектору  .
.
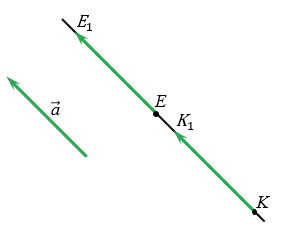
По условию точки Е и К отображаются в точки Е1 и К1 соответственно при параллельном переносе на вектор  , тогда по определению параллельного переноса
, тогда по определению параллельного переноса 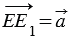 и
и 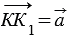 , поэтому
, поэтому  , следовательно,
, следовательно, 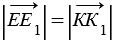 , значит, ЕЕ1 = КК1. (1)
, значит, ЕЕ1 = КК1. (1)
ЕК = КК1 + ЕК1, Е1К1= ЕЕ1 + ЕК1, тогда, учитывая (1), получим: ЕК = Е1К1, т.е. расстояние между точками Е и К равно расстоянию между точками Е1 и К1. Получаем, что параллельный перенос сохраняет расстояния между точками, значит, является частным случаем движения.
Пример
Построить 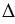 А1В1С1, который получается из
А1В1С1, который получается из 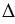 АВС параллельным переносом на вектор
АВС параллельным переносом на вектор  .
.
Дано: 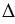 АВС, вектор
АВС, вектор  .
.
Построить: 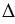 А1В1С1 параллельным переносом на вектор
А1В1С1 параллельным переносом на вектор  .
.
Решение:
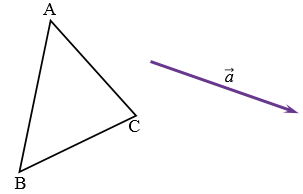
Построим точки А1, В1, С1, которые получаются из точек А, В, С соответственно, параллельным переносом на вектор  . Для этого от точек А, В и С отложим векторы, равные вектору
. Для этого от точек А, В и С отложим векторы, равные вектору  . Соединяя попарно точки А1, В1, С1 отрезками, получим искомый
. Соединяя попарно точки А1, В1, С1 отрезками, получим искомый 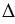 А1В1С1.
А1В1С1.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Отображение плоскости на себя
Понятие движения
Наложения и движения
Поворот
Движения
Правило встречается в следующих упражнениях:
7 класс
Задание 1162,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1163,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1164,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1165,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 14,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 15,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1178,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1179,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1182,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1301,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Определение. Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (х,у,г) фигуры переходит в точку (х+ a;y + b;z + c), где а, Ъ, с—постоянные.
Параллельный перенос в пространстве задается формулами
х» = х + а, у’ = у + b, z» = z+ с,
выражающими координаты (х», у’, z1) точки, в которую переходит точка (х,у, z) при параллельном переносе. Так же, как на плоскости, доказываются следующие свойства параллельного переноса.
1. Параллельный перенос есть движение.
2.При параллельном переносе точки смещаются по парал
лельным (или совпадающим) прямым на одно и то же расстояние.
3.При параллельном переносе каждая прямая переходит в
параллельную ей прямую (или в себя).
4.Каковы бы ни были точки ХиХ, существует единственный
параллельный перенос, при котором точка X переходит в точку X».
В пространстве добавляется еще одно свойство параллельного переноса.
5.При параллельном переносе в пространстве каждая плоскость
переходит либо в себя, либо в параллельную ей плоскость.
Докажем последнее свойство.
Пусть а — произвольная плоскость (рис. 54). Проведем в этой плоскости две пересекающиеся прямые а и ft. При параллельном переносе прямые а и Ъ переходят либо в себя, либо в параллельные прямые а1и Ь1. Плоскость а переходит в некоторую плоскость а1, проходящую через прямые а1 и б1. Если плоскость а1 не совпадает с а, то по теореме 8 она параллельна а. Что и требовалось доказать.
Вопросыи задания
1.Сколько координат имеет точка в пространстве?
2. Как найти координаты точки в пространстве?
3. Запишите формулу расстояния между двумя точками через координаты этих
точек. Имеет ли значение порядок точек и их координат?
4. Какими формулами определяются координаты середины отрезка?
15. Дайте определение параллельного переноса.
16. Перечислите свойства параллельного переноса.
Задачи
173.Даны точки А(1; 7; 4), В(3; 0; 0), С(1; 2; 0), Щ); 5; 1). Какие из этих
точек лежат: 1) в плоскости ху; 2) в плоскости у г; 3) на оси х?
174.Дана точка М(2; 4; 6). Найдите основания перпендикуляров,
опущенных из этой точки на координатные оси и координатные
плоскости.
175.Даны вершины А(1; -3; 0), В(-2; -4; 1), С(-3; 1; 1), Щ); 2; 0)
параллелограмма ABCD. Вычислите длины диагоналей паралле
лограмма.
176.Найдите расстояния от точки (2; -2; 3) до: 1) координатных
плоскостей; 2) осей координат; 3) начала координат.
177.Какая из точек: А(2; 1; 5) или В(—2; 1; 6) — лежит ближе к началу
координат?
178.При параллельном переносе точка А(3; 2; -1) переходит в точку
А2; 0; -1). В какую точку переходит начало координат?
В
179.Даны точки М (0; 1; 1), JV(2; -1; 3), 2sT(-l; у, 0). Найдите такое
значение у, чтобы выполнялось условие: МЩ = NK].
180.Найдите координаты точки, лежащей на оси у и равноудаленной
от точек Р( 4; -1; 3) и Q(l; 3; 0).
181.Найдите координаты точки, лежащей в плоскости ху и равно
удаленной от точек А(0; 1; 0), В(-1; 0; 1), С(0; -1; 0).
182.Докажите, что четырехугольник ABCD является ромбом, если:
А(0; 2; 0), ВЦ; 0; 0), С(2; 0; 2), Щ1; 2; 2).
183.Найдите координаты вершины D параллелограмма ABCD, если
координаты трех других его вершин известны:
А(4; 2; -1), Б(1; -3; 2), С(-4; 2; 1).
184. Существует ли параллельный перенос, при котором точка А пере
ходит в точку В, а точка С — в точку D, если: А(0; 1; 2), .В(-1; 0; 1),
С(3; -2; 2), Щ2; -3; 1)?
Date: 2015-04-23; view: 1664; Нарушение авторских прав
