Какие свойства имеют графы

Перед тем как начать изучение непосредственно алгоритмов, необходимо обладать базовыми знаниями касательно самих графов, понимать, как они представляются в компьютере. Здесь не будут подробно описаны все аспекты теории графов (этого и не требуется), но только те, незнание которых заметно усложнит усвоение данной области программирования.

Несколько примеров дадут немного поверхностного представления о графе. Так типичным графом является схема метро или какой-либо другой маршрут. В частности программисту знакома компьютерная сеть, также являющаяся графом. Общее здесь это наличие точек, соединенных линиями. Так в компьютерной сети точки – это отдельные серверы, а линии – различные виды электрических сигналов. В метрополитене первое – станции, второе – туннели, проложенные между ними. В теории графов точки именуется вершинами (узлами), а линии – ребрами (дугами). Таким образом, граф – это совокупность вершин, соединённых ребрами.

Математика оперирует не содержанием вещей, а их структурой, абстрагируя ее из всего того, что дано как целое. Пользуясь именно этим приемом, мы можем заключать о каких-либо объектах как о графах. А поскольку теория графов это часть математики, то для нее нет абсолютно никакого значения, что в принципе представляет собой объект; важно лишь то, является ли он графом, т. е. обладает ли обязательными для графов свойствами. Поэтому, прежде чем привести примеры, мы выделяем в рассматриваемом объекте лишь то, что как нам кажется, позволит показать аналогию, отыскиваем общее.

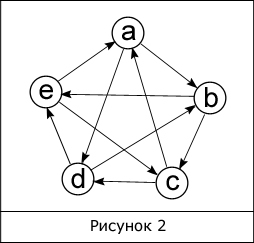
Вернемся к компьютерной сети. Она обладает определенной топологией, и может быть условно изображена в виде некоторого числа компьютеров и путей их соединяющих. На рисунке ниже в качестве примера показана полносвязная топология.

Это по сути граф. Пять компьютеров являются вершинами, а соединения (пути передачи сигналов) между ними – ребрами. Заменив компьютеры вершинами, мы получим математический объект – граф, который имеет 10 ребер и 5 вершин. Пронумеровать вершины можно произвольным образом, а не обязательно так, как это сделано на рисунке. Стоит отметить, что в данном примере не используется ни одной петли, то есть такого ребра, которое выходит из вершины и сразу же входит в нее, но петли могут встречаться в задачах.

Вот некоторые важные обозначения, используемые в теории графов:

• G=(V, E), здесь G – граф, V – его вершины, а E – ребра;
• |V| – порядок (число вершин);
• |E| – размер графа (число рёбер).

В нашем случае (рис. 1) |V|=5, |E|=10;

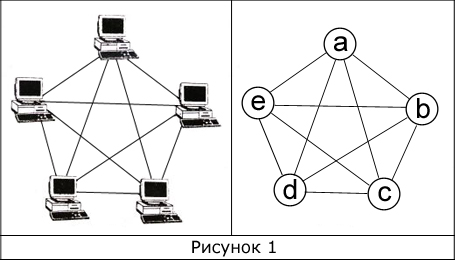
Когда из любой вершины доступна любая другая вершина, то такой граф называется неориентированным связным графом (рис. 1). Если же граф связный, но это условие не выполняется, тогда такой граф называется ориентированным или орграфом (рис. 2).

В ориентированных и неориентированных графах имеется понятие степени вершины. Степень вершины – это количество ребер, соединяющих ее с другими вершинами. Сумма всех степеней графа равна удвоенному количеству всех его ребер. Для рисунка 2 сумма всех степеней равна 20.

В орграфе, в отличие от неориентированного графа, имеется возможность двигаться из вершины h в вершину s без промежуточных вершин, лишь тогда когда ребро выходит из h и входит в s, но не наоборот.

Ориентированные графы имеют следующую форму записи:

G=(V, A), где V – вершины, A – направленные ребра.

Третий тип графов – смешанные графы (рис. 3). Они имеют как направленные ребра, так и ненаправленные. Формально смешанный граф записывается так: G=(V, E, A), где каждая из букв в скобках обозначает тоже, что ей приписывалось ранее.

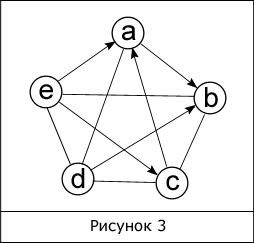
В графе на рисунке 3 одни дуги направленные [(e, a), (e, c), (a, b), (c, a), (d, b)], другие – ненаправленные [(e, d), (e, b), (d, c)…].

Два или более графов на первый взгляд могут показаться разными по своей структуре, что возникает вследствие различного их изображения. Но это не всегда так. Возьмем два графа (рис. 4).

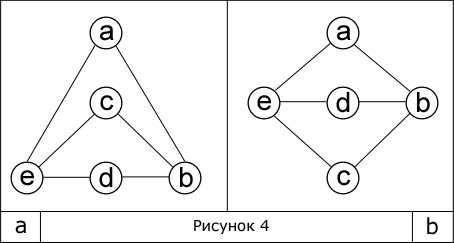
Они эквивалентны друг другу, ведь не изменяя структуру одного графа можно построить другой. Такие графы называются изоморфными, т. е. обладающими тем свойством, что какая-либо вершина с определенным числом ребер в одном графе имеет тождественную вершину в другом. На рисунке 4 изображены два изоморфных графа.

Когда каждому ребру графа поставлено в соответствие некоторое значение, называемое весом ребра, тогда такой граф взвешенный. В разных задачах в качестве веса могут выступать различные виды измерений, например длины, цены маршруты и т. п. В графическом представлении графа весовые значения указываются, как правило, рядом с ребрами.

В любом из рассмотренных нами графов имеется возможность выделить путь и, причем не один. Путь – это последовательность вершин, каждая из которых соединена с последующей посредством ребра. Если первая и последняя вершины совпадают, то такой путь называется циклом. Длина пути определяется количеством составляющих его ребер. Например, на рисунке 4.а путем служит последовательность [(e), (a), (b), (c)]. Этот путь является подграфом, так как к нему применимо определение последнего, а именно: граф G’=(V’, E’) является подграфом графа G=(V, E), только тогда когда V’ и E’ принадлежат V, E.

Способы представления графов.

Граф, как и большинство других математических объектов, может быть представлен на компьютере (сохранен в его памяти). Существуют несколько способов его интерпретации, вот наиболее известные из них:

• матрица смежности;
• матрица инцидентности;
• список смежности;
• список ребер.

Использование двух первых методов предполагает хранение графа в виде двумерного массива (матрицы). Причем размеры этих массивов, зависят от количества вершин и/или ребер в конкретном графе. Так размер матрицы смежности n×n, где n – число вершин, а матрицы инцидентности n×m, n – число вершин, m – число ребер в графе.

Похожие записи:

• Основные структуры данных.
• Матрица инцидентности.
• Список ребер графа.
• Список смежности графа.
• Матрица смежности

Так о великих вещах помогают составить понятье

Малые вещи, пути намечая для их постижения.

Лукреций

Впервые понятие «граф» ввел в 1936 г. венгерский математик Денни Кёниг. Но первая работа по теории графов принадлежала ;«перу великого Леонарда Эйлера и была написана еще в 1736 г. с помощью графов изображаются схемы различных дорог, линии воздушных сообщений, газопроводов, теплотрасс, электросетей, а также микросхемы, дискретные многошаговые процессы, системы различных бинарных отношений, химические структурные формулы и другие диаграммы и схемы. Применяются графы для решения задач химии, экономики, электротехники и автоматики. ‘Также они широко используются в информатике и строительстве. Без графов сложно анализировать классификации в различных науках.

ГрафомG = (V, X) называется пара двух конечных множеств: множество точек и множество линий X, соединяющих некоторые пары точек. В терминах декартова произведения (подразд. 1.5) подмножество множества V´V: XÌV´V.

Рис. 2.1. Примеры графов: а — со смежными вершинами; 6 — полный; в – со смежными ребрами; г — с петлей

Точки называются вершинами или узламиграфа, линии — ребрамиграфа. Примеры графов приведены на рис. 2.1.

Пусть дан граф G = (V, X), где v = [V, W, …} — конечное непустое множество его вершин, а Х(V, W) — его ребра. Если ребро графа G соединяет две его вершины V и W (т.е. <V, W>ÎX), то говорят, что это ребро им инцидентно.Две вершины графа называются смежными,если существует инцидентное им ребро: на рис. 2.1, а смежными являются вершины А и В, А и С. Если граф G имеет ребро Х(V, W), у которого начало и конец совпадают, то это ребро называется петлей.На рис. 2.1, г петля — q(С, С). Два ребра называются смежными,если они имеют общую вершину. На рис. 2.1, в смежными являются, например, ребра х1и х2с общей вершиной С.

Граф G( V, X) может иметь ребра с одинаковыми парами вида Х(V, W). Такие ребра называются кратными, или параллельными.На рис. 2.1, а кратными являются, например, ребра х1(А, В), х2(А, В). Вершинам А и В инцидентны ребра х1 х2, х3. Количество одинаковых пар вида Х(V, W) называется кратностьюребра (V, W). На рис. 2.1, а ребро АС имеет кратность, равную 3, а ребро АВ — кратность, равную 2. Число ребер, инцидентных вершине А, называется степеньюэтой вершины и обозначается deg(A) (от англ. degree — степень). Если вершине инцидентна петля, она дает вклад встепень, равный двум, так как оба конца приходят в эту вершину.

На рис. 2.1, в вершина А имеет степень, равную 1, вершина С — 4, вершина D — 2. Записывается это в виде: deg (А) = 1, deg (С) = 4, deg (D) = 2. Граф G4 (рис. 2.1, г) содержит пять вершин V= {А, В, С, , Е} и шесть ребер Х={p,q,r,s,t,u}.

Вершина графа, имеющая степень, равную нулю, называется изолированной.Граф, состоящий из изолированных вершин, называется нуль-графом.Для нуль-графа Х= Æ. Вершина графа, имеющая степень, равную 1, называется висячей.На рис. 2.1, г вершина Е — изолированная: deg(Е) = 0, а вершины А, В, Е, G,H на рис. 2.1, в — висячие.

Теорема 2.1.В графе G(V,Х) сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа: ,

где п = ïVï — число вершин; т = ïХï — число ребер графа.

Вершина называется четной (нечетной ) если ее степень четное (нечетное) число.

На рис. 2.1, в deg (D) = 2, deg (F) = 3, значит, у графа G3вершина D является четной, а F — нечетной. В теории графов доказана следующая теорема.

Теорема2.2. Число нечетных вершин любого графа — четно.

Следствие.Невозможно начертить граф с нечетным числом нечетных вершин.

Граф G называется полным,если любые две его различные вершины соединены одним и только одним ребром. Полным является граф G2на рис. 2.1, б. Таким образом, полный граф определяется только своими вершинами. Пусть число вершин полного графа п. Тогда степень любой вершины, очевидно, равна deg (V) = п — 1, а число ребер равно числу сочетаний из п по 2, т. е. т = . Число ребер также можно найти по теореме 2.1: m= .

Дополнениемграфа G(V,Х)) называется граф (V, ) с теми же вершинами V, что и граф G, и имеющий те и только те ребра , которые необходимо добавить к графу G, чтобы он стал полным. Очевидно, что граф с кратными ребрами не имеет дополнения. Например, дополнением графа G5 до графа G2 на рис. 2.1, б является граф (рис. 2.2).

Как отмечалось в подразд. 1.3, дополнением универсального множества является пустое, и наоборот. Поскольку граф и его дополнение отличаются только ребрами (множества Х, )и дополнение графов сводится к дополнению множества X , то частным случаем этого свойства будет следующее правило: дополнением полного графа будет нуль-граф, и наоборот.

Если все пары (Vi , Vj) во множестве X являются упорядоченными, т.е. кортежами длины 2, то граф называется ориентированным, орграфом,или направленным.Поскольку сразу может быть не известно, о каком графе идет речь, в этой главе мы будем употреблять круглые скобки для обозначения ребра вместо угловых, как это должно было быть для кортежей. В них будет помещаться соответствующая пара вершин. В таком случае ребра принято изображать стрелками (рис. 2.3). Началомребра называется вершина, указанная в кортеже первой, концом— вторая вершина этой пары (графически она указана стрелкой). Ребра ориентированного графа имеют определенные фиксированные начало и конец и называются дугами.Очевидно, дуги (V1, V3) и (V3, V1), если они обе существуют, различны: (V1, V3) ¹ (V3, V1).

Степенью—входа (выхода) вершины ориентированного графа называется число ребер, для которых эта вершина является концом (началом).

Степень входа вершины V будем обозначать deg +( V), а степень выхода — deg _( V)- На рис. 2.3 deg +( V1) = 1, deg +( V2) = 1, deg +( V3) = = 2, deg -( V1) = 1, deg -( V2) = 2, deg -( V3) = 1.

Дуги орграфа называются кратными,если они имеют одинаковые начальные и конечные вершины, т.е. одинаковые направления. Например, кратны дуги u(V2, V3) и t(V2, V3) на рис. 2.3.

Последовательность попарно инцидентных вершин Vi1 , Vi2, …, V ikнеориентированного графа, т.е. последовательность ребер неориентированного графа, в которой вторая вершина предыдущего ребра совпадает с первой вершиной следующего, называется маршрутом.Число ребер маршрута называется длиноймаршрута. Например, на рис. 2.1, в НСDFD — маршрут длиной 4. Обозначение: НСDFD = 4. Очевидно, что если Vi1 , Vi2, …, V ikс — маршрут длины k— 1, то и V ik, V ik-1, …, Vi2, Vi1также будет являться маршрутом длины k— 1. Маршрут принято задавать как последовательность ребер, поскольку это более удобно при наличии кратных ребер. Если начальная вершина маршрута совпадает с конечной, то такой маршрут называется замкнутымили циклом.В графе G4 (рис. 2.1, г) (t,s,p,r), (u,s,p,) — циклы длиной 4, (r,t, q s,u) — цикл длиной 5, (t,s,u,r,t,s,p,r) — 8-цикл, (р,и) — 2-цикл, петля (q) — 1-цикл.

Расстояниеммежду двумя вершинами называется минимальная длина из всех возможных маршрутов между этими вершинами при условии, что существует хотя бы один такой маршрут. Обозначается как d( V1,V2) (от лат. distantio — расстояние) d( V1,V2) = min| V1,…,V2|.

Поскольку рассматриваются конечные графы, минимум можно найти всегда. Очевидно, что d( V1,V2) = d( V2,V1). Формально можно ввести расстояние d( V ’,V ’). = 0 между любой вершиной и ей же самой, что соответствует нулевому маршруту, у которого начало и конец в одной вершине.

В маршруте одно и то же ребро может встретиться несколько раз. Если ребро встретилось только один раз, то маршрут называется цепью.Например, в графе G4 (рис. 2.1, г) (t,s, р) — 3-цепь. Если (x1 , x2, … x k-1,, x k) — k-цикл, то любая циклическая перестановка, например (, x2, … xk-1,, x k , x1), также будет k:-циклом, поскольку сведется лишь к выбору начальной вершины. Частным случаем этого утверждения будет следующее: если k-цикл (x1 , x2, … x k-1,, x k) является цепью, то для любой циклической подстановки sÎSkпоследовательность (xs(1) ,, xs(2), …, x s(k)) также будет k-циклом и цепью.

В орграфе маршрут является ориентированным и называется путем.На путь сразу налагаются важные требования, являющиеся частью определения:

• направление каждой дуги должно совпадать с направлением пути;

• ни одно ребро пути не должно встречаться дважды.

Другими словами, путь— упорядоченная последовательность ребер ориентированного графа, в которой конец предыдущего ребра совпадает с началом следующего и все ребра единственны. На рис. 2.3 (u,r,s,t) — 4-путь, (r, и) — 2-путь, (s, r, t, s) путем не является. Тогда циклв орграфе — путь, у которого совпадают начало и конец. На рис. 2.3 (r,s,t) и (и, s,r) — 3-циклы. Для циклов орграфа также справедлива теорема о циклических подстановках. Цепь, путь и цикл в графе называются простыми,если они проходят через любую из вершин не более одного раза. Неориентированный граф называется связным,если между любыми двумя его вершинами есть маршрут.Для связного графа ориентация дуг не обязательна. Так, граф G2(рис. 2.1, б) является связным, а граф G4 (рис. 2.1, г) — несвязным.Также можно ввести понятие связности для вершин графа: две вершины называются связными,если существует маршрут между ними. Понятно, что связность между вершинами является бинарным отношением. Это отношение будет отношением эквивалентности. Действительно, отноше­ние связности обладает известными свойствами (см. подразд. 1.6), т. е. оно:

рефлективно — каждая вершина (включая изолированные) связна сама с собой;

симметрично — любой маршрут (V, …, V») можно представить в обратном порядке: (V»‘, …, V ‘);

транзитивно — если вершина V соединена с вершиной V ‘ маршрутом М1(Х1 …, Хр), а вершина V ‘ соединена с вершиной V » маршрутом М2(Хр +1, …, Хп), то вершина V соединена с вершиной V» маршрутом М3(Х1 …, Хр, Хр+1, …, Хn), в котором сначала идут все ребра маршрута М1, а затем все ребра маршрута М2.

Граф G можно разбить на непересекающиеся подмножества Хi по признаку связности. Вершины одного множества являются связными между собой, а вершины различных множеств — несвязны. Тогда все подграфы Vi(классы эквивалентности) графа G называют связными компонентами, или компонентами связности.Связный граф имеет одну компоненту связности.

Доказано, что в конечном связном графе всегда можно построить ориентированный цикл, проходящий через каждое ребро по одному разу в двух направлениях. Такой цикл называют способом обхода всего графа и используют при решении многих прикладных задач. В частности, разработаны специальные алгоритмы обхода ребер графа, которые можно использовать при решении задач вида «поиска выхода из лабиринта». В лабиринте дорожки служат ребрами графа, а их разветвления, начало движения (вход) и конец (выход) — вершинами графа. Если вход и выход принадлежат одной компоненте связности, то такой лабиринт принципиально проходим, если разным — то непроходим. Во втором случае не поможет даже мифологическая «нить Ариадны».

Теорема2.3. Для того чтобы связный граф G являлся простым циклом, необходимо и достаточно, чтобы каждая его вершина имела степень, равную 2.

Ребро (V, W) связного графа G называется мостом,если после его удаления G станет несвязным и распадется на два связных графа G ‘ и G «. На рис. 2.4 мост (СЕ) разделил связный граф G7 на два различных связных графа: G ‘ с вершинами (А,В, С,D) и G » с вершинами (Е, F, G,Н,I). Также мостом является ребро ЕС.

Рис. 2.4. Граф G7 с мостами BC и CE

Теорема 2.4.Ребро графа является мостом тогда и только тогда, когда не принадлежит ни одному циклу.

Какие графы можно считать различными, а какие не различаются?

Графы G’ и G» называются изоморфными,если существует взаимно-однозначное соответствие между их ребрами и вершинами, причем соответствующие ребра соединяют соответствующие вершины. Поскольку в данном издании исследуются конечные множества, такая биекция должна быть подстановкой. Между названием вершины и ее номером различия нет. Смежность двух вершин есть бинарное отношение, поэтому изоморфизм графов можно рассматривать как изоморфизм множеств их вершин (см. подразд. 1.4 и 1.6), на котором введено отношение смежности. Итак, графы G1 (V1 , Х2) и G2( V2, Х2) называются изоморфными,если | V1| = |V2| = п и существует подстановка sÎSn, такая, что V2 = s(V1), а Х2 = {s (Vi); s( Vj)) ï (Vi, Vj)Î Х1}. Иными словами, можно так переобозначить; вершины первого графа, что в новых обозначениях вершины и ребра будут совпадать со вторым графом, причем кратным ребрам первого G ‘8 должны соответствовать кратные ребра второго G »8 такой же кратности (рис. 2.5).

Аналогично устанавливается изоморфизм между ориентированными графами. При этом следует помнить, что ребро является упорядоченным множеством, и надо быть особенно внимательным, соблюдая порядок.

Важно, что изоморфизм графов является отношением эквивалентности. Это удобнее всего заметить исходя из свойств подстановок. На практике такие различные по внешним признакам изоморфные графы не различают, рассматривая их с точностью до изоморфизма.

Граф G называется планарным (плоским),если существует изоморфный ему граф G’, в изображении которого на плоскости ребра пересекаются только в вершинах. Иными словами, у планарного графа никакие два ребра не имеют общих точек, кроме общих вершин. На рис. 2.1 графы G1и G3 являются планарными, а G2 — нет. Областьюназовем подмножество плоскости, пересекающееся с планарным графом только по некоторому проcтому циклу графа, являющемуся границей области. Поскольку рассматриваются конечные графы, то плоский граф всегда является ограниченным подмножеством плоскости. Пусть М — планарный граф с внутренними областями. Тогда дополнение М, т. е. М’ = К2М также может являться областью. Например, граф О9(рис. 2.6, а) выделяет в плоскости следующие области: А с границей д; А% с границей (о, 5, I)’, А3с границей (д, 5, и, г, {); А^с границей (р, и); А5 с границей (о, р, г). Множество Аъна рис. 2.6, б областью не является, так как пересечение Л3П С10 содержит точку (2, не принадлежащую никакому циклу.

Теорема 2.5 (Эйлера).Связный плоский граф с п вершинами и т ребрами разбивает плоскость на r областей (включая внешнюю), причем

п — т + r= 2.

Задача 17 «О трех колодцах».Проложить дорожки от трех до­мов к каждому из трех колодцев так, чтобы никакие две дорожки не пересекались (рис. 2.7).

Граф называется двудольным,если его вершины разбиты на два непересекающихся подмножества: V= V1È V2, а ребра связывают вершины только из разных классов (не обязательно все пары). Если каждая вершина множества V1связана ребром с каждой вершиной множества V2, то двудольный граф называетсяполным двудольными обозначается Кт,n, где т = | V1|, n = | V2|.

Примером двудольного полного графа К3,3, является граф к задаче 17, которую также называют «Три дома — три колодца», показывая этим два непересекающихся множества вершин графа.

На (рис. 2.8, а) граф G является планарным, так как его можно изобразить иначе (G’ на рис. 2.8, б). При таком изображении плоскость разбивается на области S1, S2, S3, S4, которые могут быть раскрашены в разные цвета. Видно, что п = 4, т = 6, r = 4, и справедлива формула Эйлера п-т + r=4-6 + 4 = 2.

Эйлеровым путем (циклом)графа G называется путь (цикл), который содержит все ребра графа только один раз. Граф, обладающий эйлероовым циклом, называется эйлеровым.Плоские эйлеровы графы можно изобразить «одним росчерком пера», причем процесс изобжения начинается и заканчивается в одной вершине. Такой граф называют также уникурсальным.

Теорема 2.6.Граф G является эйлеровым тогда и только тогда, ког