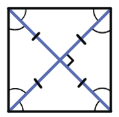
Какие общие свойства имеют ромб и квадрат
Автор:
02 апреля 2019 08:28
Мы все учили в школе геометрию, но с годами многое подзабыли. Чтобы не попасть впросак, когда ваш ребенок спросит, чем ромб отличается от квадрата, почитайте эту статью и вспомните, казалось бы, давно забытое.

Источник:
Очень часто четкое определение какого-либо предмета дает о нем практически полную информацию. Вот, например, ромб и квадрат – едва ли не самые распространенные геометрические фигуры. Глядя на них, мы понимаем, что они отличаются, но вот чем и как это объяснить простыми словами? Давайте разбираться.
Что представляет собой ромб
Источник:
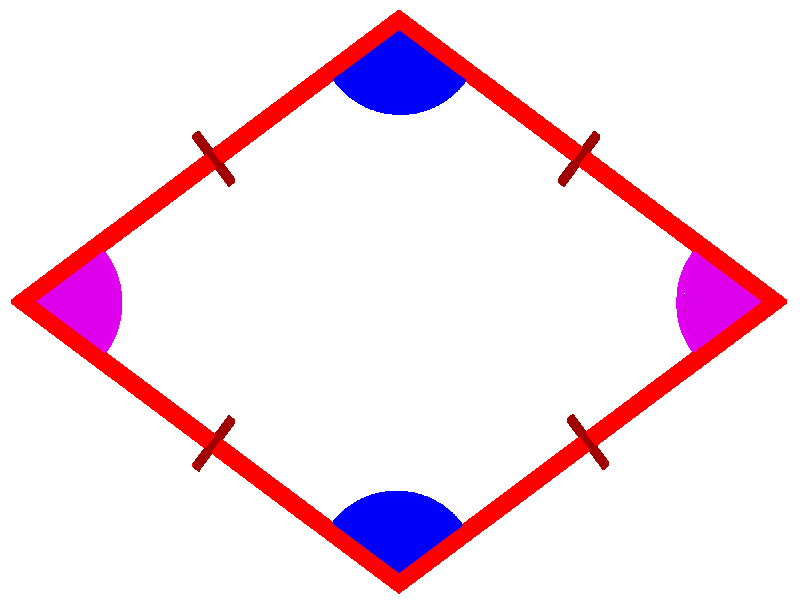
Геометрия дает такое определение ромба: «Ромбом называется параллелограмм…». Стоп, сначала придется вспомнить, что такое параллелограмм. Это многоугольник с четырьмя углами, у которого противоположные стороны параллельны. А какими же свойствами обладает ромб как разновидность параллелограмма? Вот они:
1. Если соединить противоположные углы ромба диагоналями, то углы их пересечения составят 90º, то есть они взаимно перпендикулярны.
2. Эти диагонали (вообще-то в строгой науке геометрии принято говорить «отрезки диагоналей ромба») лежат на биссектрисах, делящих его углы пополам (помните школьный стишок: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам»? Ребенку тоже будет полезно).
Что представляет собой квадрат
Источник:
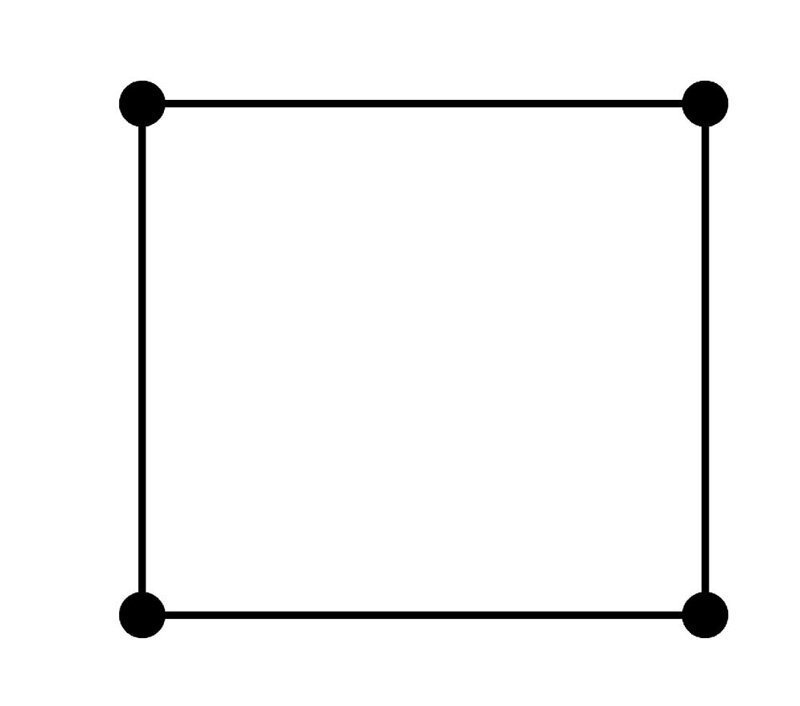
С квадратом все намного проще, его определение звучит так: квадрат — это прямоугольник, у которого все стороны равны. Теперь нужно определить, что такое прямоугольник. Это тоже параллелограмм, как и ромб, но с прямыми углами, то есть равными 90º.
Основные свойства квадрата следующие:
1. Если провести биссектрисы всех углов квадрата (напомним, что углы прямые), то отрезки диагоналей квадрата будут лежать на этих биссектрисах.
2. Если провести диагонали между противоположными углами квадрата, то в центре симметрии квадрата, где эти диагонали пересекутся, они поделятся пополам.
3. Все отрезки диагоналей квадрата будут равны между собой.
Так в чем же отличие?

Источник:
Проще всего это понять и продемонстрировать ребенку с помощью спичек или зубочисток. Возьмите 4 спички и сделайте из них ромб. Обратите внимание на то, что у ромба разные углы: 2 острых и 2 тупых. А теперь превратите ромб в квадрат – просто сдвиньте спички таким образом, чтобы все углы стали прямыми, то есть по 90º.
Таким образом, получается, что квадрат – это как бы частный случай ромба (хотя настоящему специалисту это определение может показаться не совсем научным).
Еще одно отличие заключается в том, что у квадрата диагонали равны друг другу, а у ромба одна длиннее, а другая короче.
Вывод: каждый квадрат – это ромб с прямыми углами, но не каждый ромб – это квадрат.
Источник:
Ссылки по теме:

Понравился пост? Поддержи Фишки, нажми:
У этого термина существуют и другие значения, см. Ромб (значения).
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1].
Этимология[править | править код]
Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.
Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.
Свойства[править | править код]
- Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
- Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
- Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
- Середины четырех сторон ромба являются вершинами прямоугольника.
- Диагонали ромба являются перпендикулярными осями его симметрии.
- В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Признаки[править | править код]
Параллелограмм является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:
- Две его смежные стороны равны (отсюда следует, что все стороны равны, ).
- Его диагонали пересекаются под прямым углом (AC ⊥ BD).
- Одна из диагоналей делит содержащие её углы пополам.
Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].
Квадрат, как частный случай ромба[править | править код]
Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.
Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4].
Уравнение ромба[править | править код]
Уравнение ромба с центром в точке и диагоналями, параллельными осям координат, может быть записано в виде:
где — половины длин диагоналей ромба по осям соответственно.
Длина стороны ромба равна Площадь ромба равна Левый угол ромба рассчитывается по формуле:
Второй угол дополняет его до 180°.
В случае a = b уравнение отображает повёрнутый на 45° квадрат:
где сторона квадрата равна а его диагональ равна Соответственно площадь квадрата равна
Из уравнения видно, что ромб можно рассматривать как суперэллипс степени 1.
Площадь ромба[править | править код]
- Площадь ромба равна половине произведения его диагоналей.
- Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
- Кроме того, площадь ромба может быть вычислена по формуле:
,
где — угол между двумя смежными сторонами ромба.
- Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол :
Радиус вписанной окружности[править | править код]
Радиус вписанной окружности r может быть выражен через диагонали p и q в виде:[5]
В геральдике[править | править код]
Ромб является простой геральдической фигурой.
Червлёный ромб в серебряном поле
В червлёном поле 3 сквозных ромба: 2 и 1
Просверленный червлёный ромб в серебряном поле
В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов
Симметрия[править | править код]
Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.
Ромбический орнамент
Ромбические звёзды
Более сложный орнамент
См. другие примеры на Викискладе.
См. также[править | править код]
- Дельтоид
- Звезда (геометрия)
- Ромбододекаэдр
Примечания[править | править код]
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Четырехугольники
- Ромб и квадрат
Частным видом параллелограмма является ромб.
Ромбом называется параллелограмм, у которого все стороны равны
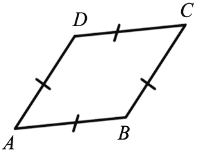
ABCD — ромб.
Ромб обладает всеми свойствами параллелограмма.
Особое свойство ромба
Доказательство
Дано: ABCD — ромб
Доказать: AC BD,
BD,  ADO =
ADO =  CDO
CDO
Доказательство:
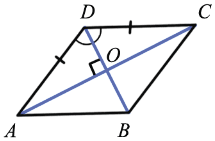
AD = DC (по определению ромба), значит,  ADC — равнобедренный.
ADC — равнобедренный.
AO = OC (по свойству диагоналей параллелограмма),  DO — медиана
DO — медиана  ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,
ADC , а в равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой,  AC
AC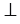 BD,
BD,  ADO =
ADO =  CDO, что и требовалось доказать.
CDO, что и требовалось доказать.
Теорема
Доказательство
Дано: ABCD — параллелограмм, AC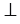 BD
BD
Доказать: ABCD — ромб
Доказательство:
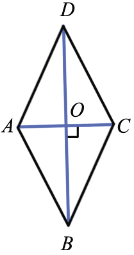
Рассмотрим  AOВ и
AOВ и  COВ:
COВ:
Т.к. AC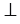 BD, то
BD, то AOВ =
AOВ =  COВ = 900;
COВ = 900;
AO = OC (по свойству диагоналей параллелограмма), ОВ — общий катет, 
 AOВ =
AOВ =  COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,
COВ (по двум катетам). В равных треугольниках против соответственно равных углов лежат равные стороны,  ВС = ВА.
ВС = ВА.
В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD — параллелограмм (по условию) AD = BC =AB = DC (по доказанному).  ABCD — ромб, что и требовалось доказать.
ABCD — ромб, что и требовалось доказать.
Теорема
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм — ромб
Доказательство
Дано: ABCD — параллелограмм, АС — диагональ и биссектриса  DAB и
DAB и DCB
DCB
Доказать: ABCD — ромб
Доказательство:
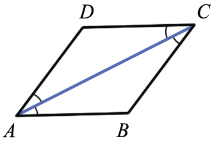
 DAB =
DAB = DCB (по свойству параллелограмма), а АС -биссектриса
DCB (по свойству параллелограмма), а АС -биссектриса  DAB и
DAB и DCB (т.е. АС делит эти углы на два равных угла),
DCB (т.е. АС делит эти углы на два равных угла), 
 DAC =
DAC =  BAC =
BAC = DCA =
DCA =  BCA
BCA
Рассмотрим  ADC:
ADC:  DAC =
DAC = DCA,
DCA, 
 ADC — равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,
ADC — равнобедренный с основанием AC, и AD = DC. В параллелограмме противоположные стороны равны,  AD = BC, AB = DC
AD = BC, AB = DC
Итак: ABCD — параллелограмм (по условию) AD = BC =AB = DC (по доказанному).  ABCD — ромб, что и требовалось доказать.
ABCD — ромб, что и требовалось доказать.
Две теоремы, доказанные выше, называют признаками ромба.
Основные свойства квадрата:
1. Все углы квадрата прямые.
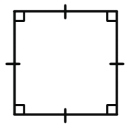
2. Диагонали квадрата равны, взаимно перпендикулярны, точкой пересечения делятся пополам и делят углы квадрата пополам.

Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Многоугольник
Выпуклый многоугольник
Четырехугольник
Параллелограмм
Признаки параллелограмма
Трапеция
Прямоугольник
Осевая и центральная симметрии
Четырехугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 409,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 441,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 500,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 762,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 825,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 997,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1130,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1136,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1212,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Конспект урока. 8 класс (учебник Л.С.Атанасян)
Тема урока: Ромб, квадрат и их свойства
Тип урока:
1) по основной дидактической цели: урок открытия нового знания.
2) по основному способу проведения: сочетание различных форм занятий.
3)по форме проведения: комбинированный урок.
Цели урока: Создание условий для усвоения учащимися понятий ромба, квадрата, их свойств.
Задачи урока:
1) образовательные:
Формировать:
-понятия ромба и квадрата как частных видов параллелограмма;
-умение формулировать свойства ромба, квадрата;
-умение построения ромба и квадрата;
-умения применять свойства ромба и квадрата при решении задач.
2) Развивающие:
-Развивать мышление, память, математический язык, осуществлять самостоятельную деятельность на уроке.
-Развивать умения систематизировать полученные знания.
-Развивать умение высказывать свое мнение, делать выводы;
Формы обучения: индивидуальная, фронтальная, групповая.
Оборудование: доска, мультимедиа, карточки с заданиями, раздаточный материал с заданиями.
План урока:
I . Организационный момент
II. Актуализация опорных знаний
III. Формирование новых знаний
IV. Применение знаний, формирование умений и навыков.
V. Теоретическая самостоятельная работа.
VI. Постановка домашнего задания
VII. Подведение итогов урока
VIII. Рефлексия
I. Организационный момент
Приветствие. Проверка готовности к уроку.
2. Мотивация учебной деятельности учащихся.
II. Актуализация опорных знаний.
Мы с вами изучили свойства и признаки некоторых четырехугольников. Перед вами лист с четырехугольниками. Какие четырехугольники из изображенных на листе вы знаете? Для каких четырехугольников знаете точные определения и свойства? А какие известны по форме, но определения и свойств этих свойств не знаете? Да это квадрат и ромб, с понятием квадрата вы встречались ещё в начальной школе, да и ромб фигура- знакома.
Чтобы узнать их определения и свойства нам не обойтись без знаний полученных ранее. Мы их проверим, выполнив следующую работу. Возьмите лист № 1. На листе вопросы. Если вы согласны с предложением ставьте «да», если не согласны ставьте «нет». Ответы появятся на доске через 3 мин. Если появляются вопросы у учащихся, то на них отвечают или учащиеся или учитель. Приводятся примеры.
п/п
Вопрос
Данет
Является ли прямоугольником параллелограмм, у которого есть прямой угол?
Верно ли, что каждый прямоугольник является параллелограммом?
Верно ли, что каждый параллелограмм является прямоугольником?
Диагонали параллелограмма равны 4 и 5 дм. Является ли этот параллелограмм прямоугольником?
Диагонали четырехугольника равны. Обязательно ли этот четырехугольник прямоугольник?
6.
Верно ли, что в каждом четырехугольнике сумма углов составляет 3600.
7.
Верно ли, что в каждом четырехугольнике сумма соседних углов равна 1800
8.
Верно ли, что в каждом четырехугольнике противоположные углы равны.
III. Формирование новых знаний.
Сегодня Вам предстоит самостоятельно изучить новый материал. Сейчас откроете учебник на стр.109. Читая текст, вы делает пометки на полях: слайд 4
V – уже знал;
+ – новое;
– – думал иначе;
? – не понял, есть вопросы.
Затем вам предстоит заполнить таблицу, это лист №2. Записи делайте краткие, ключевые слова, фразы.
Лист №2
Определения
Свойства, особые свойства.
ромб
1.
2.
3.
4.
5.
6.
квадрат
1.
2.
3.
4.
5.
6.
Кстати: Ромб (от греч.) бубен. Если сейчас бубны делают круглой формы, то раньше их делали как раз в форме ромба. От тех времен дошли ромбики на картах.
После заполнения учащимися таблицы обобщаем результаты работы в режиме беседы. Даются определения, перечисляются свойства фигур (ромба, квадрата), находят общие свойства. Если у обучающихся возникли вопросы, то отвечаю на них, предварительно выяснив, не может ли кто-то из обучающихся ответить на возникший вопрос. ( Этот приём способствует развитию умения классифицировать, систематизировать поступающую информацию, выделять новое.)
Конечно, при решении задач на уроках так и в жизни используются свойства фигур.
Например: Ромб, в котором проведены диагонали, считается одной из самых крепких и выносливых конструкций. Такую конструкцию очень широко используют для постройки мостов, зданий, и даже, для рамы мотоцикла.
Вы выяснили, каким особым свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам. Нам необходимо доказать это свойство. Работа в парах. Задача пар: прочитать доказательство, определить основную идею. Желающие доказывают у доски, остальные учащиеся следят за доказательством, задают вопросы.
IV. Применение знаний, формирование умений и навыков.
Теперь зная свойства ромба, решите задачу. Два ученика решают у доски.
Задача1 .
Найдите периметр ромба ABCD, если ∟ В =120 ◦, а диагональ BD = 20 см. (Ответ: 20 см) рис.на доске. Наводящие вопросы:
— Что называют периметром?
— Как найти периметр ромба?
— Каким свойством обладают диагонали ромба?
— Свойства равностороннего треугольника?
Задача 2. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 300 меньше другого. Чертёж сделать самостоятельно. (Ответ: 300 и 600).
После решения идет обсуждение решённых задач.
V. Теоретическая самостоятельная работа.
— Заполните таблицу, отметив знаки + (да) и – (нет).
Лист № 3.
параллелограмм
прямоугольник
ромб
ввадрат
1.
Все стороны равны
2.
Все углы равны
3.
Противоположные стороны параллельны и равны
4.
Противоположные углы равны
5.
Сумма соседних углов равна 1800
6.
Все углы прямые
7.
Диагонали равны
8.
Диагонали пересекаются и точкой пресечения делятся пополам.
9.
Диагонали являются биссектрисами углов
10.
Диагонали взаимно перпендикулярны
параллелограмм
прямоугольник
ромб
квадрат
1.
Все стороны равны
_
_
+
+
2.
Все углы равны
_
+
+
3.
Противоположные стороны параллельны и равны
+
+
+
+
4.
Противоположные углы равны
+
+
+
+
5.
Сумма соседних углов равна 1800
+
+
+
+
6.
Все углы прямые
_
+
_
+
7.
Диагонали равны
_
+
_
+
8.
Диагонали пересекаются и точкой пресечения делятся пополам.
+
+
+
+
9.
Диагонали являются биссектрисами углов
_
_
+
+
10.
Диагонали взаимно перпендикулярны
_
_
+
+
Самостоятельную проверить и поставьте себе оценку.
Критерии выставления оценки:
Оценка «5» — все ответы верные.
Оценка «4» — допущены 1, 2 ошибки.
Оценка «3» — допущены 3-5 ошибки.
Оценка «2» — допущены более 5 ошибок.
VI. Домашнее задание: 1. п.п.47. Выучить определения и свойства ромба и квадрата. Уметь доказывать теорему, выражающую особое свойство ромба. №№ 406,407.
VII. Подведение итогов урока
Выставить оценки за работу на уроке наиболее активным учащимся и кто выполнил
работу по уровням.
VIII. Рефлексия.
Важна ли сегодняшняя тема урока. Если да, то обоснуйте.
Какие новые понятия изучили?
Что узнали нового и чему научились на уроке?
Чтобы хотели узнать ещё по данной теме?
