Какие бывают свойства вычитания

Операции вычитания между любыми натуральными числами присущ ряд особенностей, называемых свойствами. В данной статье мы рассмотрим основные свойства натуральных чисел и приведем разъясняющие примеры.
Свойство вычитания равных натуральных чисел
Свойство вычитания двух равных натуральных чисел
Для двух равных натуральных чисел их разность равна нолю. Если a — любое натуральное число, то a-a=0.
Это самое простое свойство. Число ноль указывает на отсутствие чего либо. Если из множества каких-то объектов вычесть такое же множество объектов, получится ноль. Например, у Пети было 15 яблок, он решил угостить Машу и отдал ей все 15 штук. Теперь у Пети ноль яблок.
Переместительный закон (не выполняется для вычитания)
Известно, что при сложении чисел от перемены мест слагаемых сумма не меняется. Так же, как и при умножении произведение не меняется при перестановке множителей. Эта особенность называется переместительным, или коммутативным законом. Однако при вычитании коммутативный закон работает только в одном случае: когда вычитаемое число равно уменьшаемому.
В случаях, когда уменьшаемое число становится меньше вычитаемого, теряется сам смысл вычитания натуральных чисел. Например:
38-21 очевидно, не равно 21-38
В общем виде можно записать это так: a-b≠b-a.
Свойства вычитания натуральных чисел
Для операции вычитания натуральных чисел переместительный закон не выполняется!
Вычитание суммы двух чисел из натурального числа
Сформулируем свойство, а затем рассмотрим пример, который даст глубокое понимание и поможет осмыслить сказанное.
Свойство вычитания суммы двух чисел из натурального числа
Вычитание суммы двух натуральных чисел из другого натурального числа равносильно последовательному вычитанию из числа сначала одного слагаемого суммы, а затем другого.
Математически это запишется так:
a-(b+c)=(a-b)-c
Обратимся к примеру. У Пети и у Васи было по 8 монет. Петя сразу купил напиток за две монеты и конфету за одну монету. Вася сначала купил напиток, а потом подумал, и тоже купил конфету. В итоге, у обоих осталось по пять монет. Операции с монетами Пети и Васи можно соответственно записать так:
8-(2+1)=5(8-2)-1=5
Важно отметить, что данная операция для натуральных чисел имеет смысл только тогда, когда уменьшаемое число больше или равно сумме чисел, которые из него вычитают.
В соответствии с рассмотренным свойством и сочетательным законом, можно вычитать из натурального числа сумму двух, трех и более чисел.
Вычитание числа из суммы
Представим, что у Родиона в одном кармане 3 конфеты, а в другом — 5 конфет. 2 конфеты он обещал отдать Зухре. Какими способами может Родион отдать Зухре конфеты?
Во-первых, можно все конфеты переложить в один карман и оттуда уже достать 2 штуки. Останется конфет: 3+5-2.
Во-вторых, можно сразу достать две конфеты из первого кармана. Останется конфет: 3+5-2.
Наконец, в-третьих, можно достать две конфеты из второго кармана. В итоге имеем: 5+(3-2).
Количество конфет в итоге остается неизменным и справедливы равенства:
3+5-2=5+(3-2)=(3+5)-2.
Теперь можно сформулировать правило вычитания числа из суммы других натуральных чисел.
Свойство вычитания натурального числа из суммы двух чисел
Вычитание натурального числа из суммы других натуральных чисел эквивалентно последовательному вычитанию данного числа из одного слагаемого и сложению полученной разности с другим слагаемым.
В буквенной форме свойство имеет следующий вид:
(a+b)-c=(a-c)+b
Если выполняется условие b≥c, можно записать (a+b)-c=a+(b-c).
При a≥c и b≥c оба равенства можно переписать в виде (a+b)-c=(a-c)+b=a+(b-c).
Свойство вычитания натурального числа из суммы трех и более чисел формулируется аналогично и вытекает из свойства вычитания числа из суммы двух чисел.
Рассмотрим пример.
Пример. Вычитание числа из суммы
a, b, c, d — некоторые натуральные числа.
Если a≥d то a+b+c-d=(a-d)+b+c.
Если b≥d то a+b+c-d=a+(b-d)+c.
Если c≥d то a+b+c-d=a+b+(c-d).
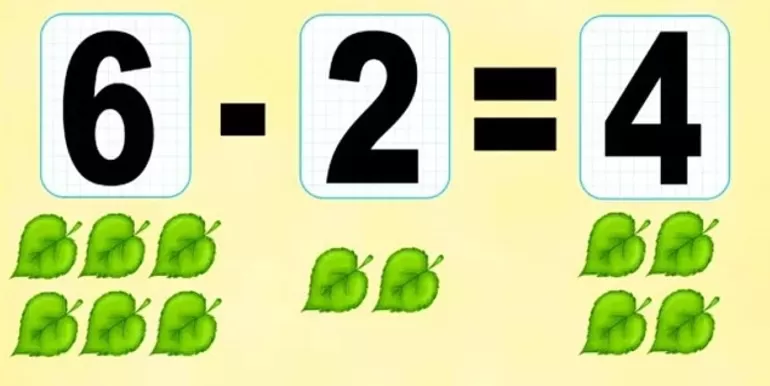
Понятие действия
Вычитание — бинарная операция, результатом выполнения которой является число, называемое разностью. В действии участвуют два аргумента: один из них — уменьшаемое, а другой — вычитаемое. Ответ получается путем уменьшения значения одного аргумента на второй. Уменьшаемое располагается слева, а вычитаемое — справа. Обозначают операцию знаком минус, который ставят между двумя числами. По сути, уменьшение — это действие, обратное сложению.
При операции вычитания используют три термина:
- Разность — ответ, полученный после выполнения действия.
- Уменьшаемое — часть выражения, которое нужно уменьшить.
- Вычитаемое — определяет величину уменьшения.
Стоит отметить, что результат вычитания может быть как положительным, так и отрицательным. Рассмотреть процесс уменьшения удобно на примере:
Пусть в вазе лежит восемь яблок. Если три штуки забрать, то в вазе останется пять.
Математическая запись такого действия будет выглядеть как 8 — 3 = 5. В ней число восемь является уменьшаемым, три — вычитаемым, а пять — разностью (результатом). Произносится эта запись так: разность восьми и трёх равняется пяти.
Применение вычитание также позволяет сравнивать два числа. Пытаясь вычислить, какое число больше, а какое меньше, фактически определяют ту часть выражения, где находится больше единиц. Найти же, какое число больше или меньше другого, можно как раз вычитанием. Например для того чтобы узнать, насколько 50 меньше 80, нужно из последнего вычесть первое: 80 — 50 = 30. То есть второе число больше первого на тридцать единиц.
Так как уменьшение — это операция, обратная суммированию (прибавлению), то проверкой вычитания будет сумма. Пусть дано равенство: 66 — 13 = 43. Чтобы проверить его верность, можно к тринадцати (вычитаемому) прибавить разность (ответ). В результате должно получиться число, равное уменьшаемому. Для рассматриваемого примера проверка выглядит следующим образом: 13 + 43 = 66. Осуществить проверку можно и другим способом. Для этого необходимо уменьшаемое уменьшить на разность. Если после действия ответ совпадет с вычитаемым, то задание решено верно: 66 — 43 = 13.
Уменьшение многозначных чисел обычно выполняют в столбик. Для этого друг под другом пишут уменьшаемое и вычитаемое таким образом, чтобы разряды чисел находились строго один под одним. Затем проводят черту и, начиная с наименьшего разряда, выполняют минусование. Результат записывают под чертой.
Свойства уменьшения
Основная формула вычитания имеет следующий вид: a — b = c. При этом справедливыми будут утверждения: с + b = a и a — c = b. Числа, подставляемые в формулу, могут быть любыми, например натуральными, дробными, рациональными. Но вычитать можно только те аргументы, которые принадлежат одному множеству, то есть относятся к одному типу. Действие характеризуется несколькими важными свойствами:

- Вычитание нулевого элемента не изменит уменьшаемое. Если же уменьшается ноль, то в ответе получится вычитаемое с отрицательным знаком. Таким образом, при вычитании некого числа аргумент уменьшается на определенное число единиц. Если же из уменьшаемого отнять такое же число, то результатом будет ноль. Математические записи, описывающие эти свойства, следующие: a — 0 = a; a — a = 0; 0 — a = -a.
- При вычитании суммы из числа можно сначала вычесть из этого числа слагаемое, а затем из полученного результата отнять второе слагаемое: a — (b + c) = a — b — c. Аналогично можно поступить и для вычитания числа из суммы: (a + b) — c = (a — c) + b = a + (b — c).
- Чтобы сложить разность и число, можно прибавить уменьшаемое, а уже и из рассчитанной суммы вычесть вычитаемое: а + (b — c) = a + b — c.
Кроме этого, действие характеризуется антикоммутативностью — правило позволяет поменять аргументы местами, но при этом перед действием необходимо поставить знак минус, и дистрибутивностью — сочетанием умножения и вычитания. Других правил не бывает.
Если рассмотреть процесс на графике, то можно говорить, что происходит перенос числа по числовой прямой в левую часть. Следует отметить, что если действие выполняется с отрицательным числом, то получится операция сложения, так как минус на минус будет давать плюс. В этом случае результат сместится в правую часть. Важным является и то, что при вычитании переместительный закон, как для сложения или умножения, выполняться не будет. Действительно, очевидно, что 4 — 2 не будет равняться 2 — 4.
Этим базисным понятиям арифметики начинают обучать в 5 классе. Правила и свойства сложения и вычитания помогают довольно сильно облегчить ту или иную задачу. Так, чтобы вычесть сумму чисел из натурального аргумента, можно сначала найти сумму, а потом выполнить вычитание. Но, используя правило, может быть и удобнее сначала выполнить уменьшение, а потом разность прибавить к числу. Например, 38 — (28 + 7). Здесь проще сначала от тридцати восьми отнять двадцать восемь, а потом прибавить семь, чем сначала выполнять действие в скобках.
Простые примеры
Знание правил должно быть обязательно подкреплено практическим навыком. Поэтому как в школе, так и в видеоуроках после прослушивания лекции учащимся предлагается решить несколько примеров. Вначале школьники делают вычисления совместно с преподавателем, который должен рассказать, как лучше поступить в том или ином задании. Затем уже ученикам нужно попробовать самостоятельно порешать примеры. Для этого используют математические тренажеры.
Вот один из них, состоящий из 15 тестов и затрагивающий различные правила:
- 2 — 1 = 1;
- 35 — 5 = 30;
- 100 — 41 = 59;
- 700 — 545 = 155;
- 1 + 1 — 2 = 0 = 2 — 2 = 0;
- 345 — 0 = 345;
- 0 — 15 = -15;
- 12275 — 12275 = 0;
- 32 + 0 — 1 = 32 — 1 = 31;
- 139 — (10 + 39) = 139 — 39 + 10 = 100 + 10 = 110;
- (123 + 17) — 33 = (123 — 33) + 17 = 90 +17 = 107;
- (201 — 11 + 1379) — 1379 = (201 — 11) + (1379 — 1379) = 190 + 0 = 190;
- 545 — (402 — 35) = 545 + 402 — 35 = 545 — 35 — 402 = 510 — 402 = 108;
- 32 — 76 + 96 — 76 — 32 = (32 — 32) — (76 — 76) + 96 = 96;
- 3 — 6 — 50 + 2 + 1 = (3 + 2 + 1) — 6 — 50 = 6 — 6 — 50 = 0 — 50 = -50.
Только с опытом можно понять, в каких случаях желательно использовать переместительное правило, а в каких удобнее применить сочетательный закон без изменения записи.

Пример. Пусть у Ирины Петровны на кредитной карте находилось 3282 рубля. В конце месяца ей на эту карту начислили 6018 рублей пенсии. Ирина Петровна в магазине купила себе пирог и рассчиталась картой. Стоимость покупки составила 318 рублей. Спрашивается, сколько денег осталось у пенсионерки на счету. Эту задачу можно решить тремя разными способами. Какой из них удобнее, зависит от личного предпочтения:
- (3282 + 6018) — 318 = 9300 — 318 = 8982.
- 3282 — 318 + 6018 = 2964 + 6018 = 8982.
- 6018 — 318 + 3282 = 5700 + 3282 = 8982.
Таким образом, какой бы способ ни был выбран, можно утверждать, что у Ирины Петровны на карте после покупки останется 8982 рубля. После окончания 5 класса законы вычитания нужно знать так же хорошо, как и таблицу умножения. Только в этом случае от арифметики можно будет переходить к изучению алгебры.
Вычитание на числовой прямой
Довольно наглядно свойства вычитания можно увидеть на иллюстрации, изобразив действие на числовой прямой. На ней нужно отложить точки через равный промежуток, например от ноля до десяти, и последовательно их пронумеровать.
Так, для решения примера 3 + 5 — 2 на прямой необходимо найти цифру три. Согласно условию и свойствам уменьшения, из неё можно вычесть двойку. Следовательно, нужно влево от тройки отсчитать два пункта. На иллюстрации этому будет соответствовать точка один. Затем по условию задания нужно прибавить пять единиц. На графике этому будет соответствовать перемещение на пять точек вправо. Итогом всех действий получится точка, подписанная как шесть.
Аналогичным образом можно подсчитать любое вычитание или сложение. Но этот метод хорош для обучения при значениях не больше десяти. Очень наглядно иллюстрация показывает и вычитание ноля. Так как при уменьшении на ноль передвигаться по прямой не нужно, то после вычитания значение уменьшаемого не изменяется.

Задача 1. Пусть имеется отрезок АБ. Нужно определить его длину, если известно, что первой точке (А) соответствует число минус пять, а второй (Б) — девять. На прямой нужно отложить ноль и по обе стороны от него отметить точку, соответствующую минус пяти и девяти. Согласно условию, задачу можно записать как -5 + АБ = 9.

Отсюда следует, что АБ = 9 — (- 5). Сформулировав в уме правило, что минус на минус даёт плюс, равенство верно будет переписать как АБ = 9 + 5 = 14. Проверку можно выполнить, уменьшив результат на пять: АБ — 5 = 9. А можно на графике отсчитать в правую сторону четырнадцать отрезков. Последний из них должен будет совпадать с числом -5.
Задача 2. Велосипедист за день преодолел путь от села Крюково до деревни Морозко. Вычислить, какое он преодолел расстояние за первый час, если за следующее время он проехал 13 км. Для иллюстрации условия задачи нужно на прямой изобразить точку отсчёта, обозначив её за ноль. Затем отметить конечную точку, соответствующую 18 км (в удобном масштабе).
На прямой от конечной точки отсчитать 13. Теперь от тринадцати подсчитать количество отрезков до начальной точки. Математические же вычисления будут выглядеть так: 18 — 13 = 4 км. И в первом, и во втором случае ответ будет аналогичным.
Вычита́ние (убавление) — одна из вспомогательных бинарных математических операций (арифметических действий) двух аргументов (уменьшаемого и вычитаемого), результатом которой является новое число (разность)[1], получаемое уменьшением значения первого аргумента на значение второго аргумента. На письме обычно обозначается с помощью знака «минус»: . Вычитание — операция обратная сложению.
В общем виде можно записать: , где и . То есть каждой паре элементов из множества ставится в соответствие элемент , называемый разностью и .
Вычитание возможно только, если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип).
При наличии отрицательных чисел, вычитание удобно рассматривать (и определять) как разновидность сложения — сложение с отрицательным числом[2]. К примеру, можно рассматривать как сложение: .
На множестве вещественных чисел область значений функции сложения графически имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов.
У вычитания есть несколько важных свойств (например для ):
Антикоммутативность:
Неассоциативность:
Дистрибутивность:
Вычитание (нулевого элемента) даёт число равное исходному:
В качестве примера, на картинке справа запись обозначает пять яблок вычесть два яблока, что в результате дает три яблока. Заметим, что нельзя вычесть например из 5 яблок 2 груши. Помимо счета яблок, вычитание также может представлять разность других физических и абстрактных величин, таких как: отрицательные числа, дробные числа, векторы, функции, и другие.
Формы записи и терминология[править | править код]
Вычитание записывается с использованием символа «минус»: «» между аргументами, такая форма записи называется инфиксной нотацией. В данном контексте символ «минус» является бинарным оператором. Результат записывается с использованием знака равенства «», например:
;
(«шесть минус три равно три») ;
(«шестьдесят четыре минус тридцать пять равно двадцать девять») .
На письме символ «минус» очень похож на другие письменные символы «дефис», «тире» и другие. Следует внимательнее разбирать выражение, чтобы не возникло ошибочного истолкования символа.
Свойства[править | править код]
Операция вычитание на числовых множествах имеет следующие основные свойства:
- Вычитание антикоммутативно — от перемены мест аргументов разность изменяется:
Антикоммутативность:
- Вычитание антиассоциативно — при последовательном выполнении вычитания трёх или более чисел последовательность выполнения операций имеет значение, результат изменится:
Антиассоциативность:
- Вычитание дистрибутивно, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве, также известно, как распределительный закон[4] .
Дистрибутивность:
- Относительно вычитания в множестве существует единственный нейтральный элемент, вычитание из числа нулевого (или нейтрального элемента) даёт число равное исходному:
Нулевой элемент:
- Вычитание нуля идемпотентно — повторное применение операции к объекту даёт тот же результат, что и одинарное:
Идемпотентность: ;
- Вычитание противоположного элемента даёт удвоенное число:
Результат вычитания не всегда является определённым для множества натуральных чисел : чтобы получить натуральное число в результате вычитания, уменьшаемое должно быть больше вычитаемого. Невозможно в рамках натуральных чисел вычесть из меньшего числа большее.
Операция вычитания чисел определённых на множествах даёт число (разность) принадлежащее этому же множеству, следовательно операция вычитание относится к замкнутым операциям (операциям, не выводящим результат из данного множества чисел), то есть множества чисел образуют кольца относительно операции вычитания.
Выполнение вычитания[править | править код]
Операцию вычитания можно представить, как некий «черный ящик» с уменьшаемым и вычитаемым на входе и одним выходом — разностью:
При практическом решении задачи вычитания двух чисел необходимо свести её к последовательности более простых операций: «простое вычитание», заём, сравнение и др. Для этого разработаны различные методы вычитания, например для чисел, дробей, векторов и др. На множестве натуральных чисел в настоящее время используется алгоритм поразрядного вычитания. При этом следует рассматривать вычитание как процедуру (в отличие от операции).
Примерный алгоритм процедуры поразрядного вычитания двух чисел
Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при вычитании больших чисел может занять продолжительное время.
Пример пошагового вычитания из числа 6 числа 4 на числовой прямой.
«Простое вычитание» — в данном контексте обозначает операцию вычитания чисел меньше двадцати, которая может быть легко сведена к декрементированию. Является гипероператором декрементирования:
где: — последовательность операций инкрементирования, выполненная раз;
— последовательность операция декрементирования, выполненная раз.
Чтобы упростить и ускорить процесс вычитания используют табличный метод «простого вычитания», для этого заранее вычисляют все комбинации разностей чисел от 18 до 0 и берут готовый результат из этой таблицы [5]:
таблица для вычитания в десятичной системе счисления
| — | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 3 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 4 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 5 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 6 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 7 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 8 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||||||||
| 9 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
Данная процедура применима к вычитанию натуральных и целых (с учётом знака) чисел. Для других чисел используются более сложные алгоритмы.
Вычитание чисел[править | править код]
Натуральные числа[править | править код]
Воспользуемся определением натуральных чисел как классов эквивалентности конечных множеств. Обозначим классы эквивалентности конечных множеств порождённых биекциями, с помощью скобок: . Тогда арифметическая операция «вычитание» определяется следующим образом:
где — разность множеств. Данная операция на классах введена корректно, то есть не зависит от выбора элементов классов, и совпадает с индуктивным определением.
Взаимно однозначное отображение конечного множества на отрезок можно понимать как нумерацию элементов множества . Этот процесс нумерации называют «СЧЕТОМ». Таким образом, «счет» — это установление взаимно однозначного соответствия между элементами множества и отрезком натурального ряда чисел.
Для вычитания натуральных чисел в позиционной системе обозначения чисел применяется поразрядный алгоритм вычитания. Если даны два натуральных числа и такие, что:
где ; — количество цифр в числе ; — порядковый номером разряда (позиции), ; — основание системы счисления; множество числовых знаков (цифр), конкретной системы счисления: , , ; тогда:
вычитая поразрядно, получаем:
Таким образом операция вычитания сводится к процедуре последовательного простого вычитания натуральных чисел , с формированием заёма при необходимости, которое производится либо табличным методом, либо декрементированием (счетом).
Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и в десятичной системе, так как все они основываются на правилах выполнения действий над соответствующими многочленами. При этом нужно пользоваться таблицей вычитания, соответствующей данному основанию системы счисления.
Пример вычитания натуральных чисел в двоичной, десятичной и шестнадцатеричной системах счисления, для удобства числа записываются друг под другом соответственно разрядам, знак заёма пишется сверху, недостающие разряды дополняются нулями:
Целые числа[править | править код]
Множество целых чисел — расширение множества натуральных чисел , получаемое добавлением отрицательных чисел [6] вида . Множество целых чисел обозначается Арифметические операции над целыми числами определяются как непрерывное продолжение соответствующих операций над натуральными числами.
Положительное и отрицательное числа на числовой прямой.
Наличие отрицательных чисел позволяет рассматривать (и определять) «вычитание» как разновидность «сложения» — сложение с отрицательным числом. Однако рассмотрим в рамках данной статьи «вычитание», как операцию определённую на множестве целых чисел, это также относится и к следующим числовым множествам. Отличие от натуральных чисел состоит в том, что отрицательные числа на числовой прямой направлены в противоположную сторону, это несколько меняет процедуру вычитания. Необходимо учитывать взаимное направление чисел, здесь возможны несколько случаев:
Здесь и далее также используется алгоритм поразрядного вычитания (сложения). Например, рассмотрим выражение: ; так как у чисел и разные знаки, то выносим минус за скобки: , вычисляя далее получим ответ: .
Рациональные числа[править | править код]
Множество рациональных чисел обозначается (от англ. quotient «частное») и может быть записано в таком виде:
Для вычитания рациональных чисел в виде обыкновенных (или простых) дробей вида: , их следует преобразовать (привести) к общему (одинаковому) знаменателю. Например, взять произведение знаменателей, числители при этом умножаются на соответствующие знаменатели. Затем вычесть полученные числители, а произведение знаменателей станет общим.
Если даны два рациональных числа и такие, что: (дроби не сокращаемые), тогда:
[7]
Либо можно найти наименьшее общее кратное (НОК) знаменателей. Порядок действий:
После этого знаменатели обеих дробей совпадают (равны ). В ряде простых случаев это упрощает вычисления, но в случае больших чисел расчёты значительно усложняются. Можно взять в качестве любое другое общее кратное.
Пример вычитания:
Если знаменатели обеих дробей совпадают, то:
Если знаменатели кратны какому либо числу, то преобразуем только одну дробь:
Арифметическая операция «вычитание» над рациональными числами относится к замкнутым операциям.
Вещественные числа[править | править код]
Арифметические операции над вещественными числами представимых бесконечными десятичными дробями определяются как непрерывное продолжение[8] соответствующих операций над рациональными числами.
Если даны два вещественных числа, представимые бесконечными десятичными дробями:
,
определённые соответственно фундаментальными последовательностями рациональных чисел (удовлетворяющие условию Коши), обозначенные как: и , то их разностью называют число , определённое разностью последовательностей и :
;
вещественное число , удовлетворяет следующему условию:
.
Таким образом разностью двух вещественных чисел и является такое вещественное число которое содержится между всеми разностями вида с одной стороны и всеми разностями вида с другой стороны[9].
На практике для того, чтобы вычесть два числа и , необходимо заменить их с требуемой точностью приближёнными рациональными числами и . За приближенное значение разности чисел берут разность указанных рациональных чисел . При этом не важно, с какой стороны (по недостатку или по избытку) взятые рациональные числа приближают и . Сложение производится по алгоритму поразрядного сложения.
При вычитании приближённых чисел их абсолютные погрешности складываются , абсолютная погрешность числа принимается равной половине последнего знака этого числа. Относительная погрешность разности заключена между наибольшим и наименьшим значениями относительных погрешностей аргументов; на практике принимается наибольшее значение . Полученный результат округляют до первой верной значащей цифры, значащая цифра приближенного числа является верной, если абсолютная погрешность числа не превосходит половины единицы разряда, соответствующего этой цифре.
Пример вычитания , с точностью до 3-го знака после запятой:
График[править | править код]
На множестве вещественных чисел область значений функции вычитания графически имеет вид плоскости проходящей через начало координат и наклоненной к осям на 45° угловых градусов.
Так как , то и для этих множеств область значений функции вычитания будет принадлежать этой плоскости.
Комплексные числа[править | править код]
Вычитание двух комплексных c=a-b чисел может быть представлено геометрически через построение треугольника.
Множество комплексных чисел с арифметическими операциями является полем и обычно обозначается символом .
Комплексные числа вычитаются друг с другом путём вычитания действительных и мнимых частей[10]. Это значит, что:
Где: , — мнимая единица. Используя представление комплексных чисел как векторов на комплексной плоскости, можно дать вычитанию комплексных чисел следующую геометрическую интерпретацию: разностью комплексных чисел и , представленных векторами на комплексной плоскости, будет вектор, соединяющий концы уменьшаемого вектора и вычитаемого вектора и направленный от вычитаемого к уменьшаемому, он является разностью векторов и соответственно разностью комплексных чисел (аналогично будет если к уменьшаемому вектору прибавить вектор обратный вычитаемому вектору).
Аналогично для комплексных чисел n-ой размерности:
Экспоненциальная запись[править | править код]
В экспоненциальной записи числа записываются в виде , где — мантисса, — характеристика числа, — основание системы счисления. Для вычитания двух чисел, которые записаны в экспоненциальной форме, требуется, чтобы у них были одинаковые характеристики: согласно свойству дистрибутивности.
Например:
Вычитание произвольных чисел[править | править код]
При вычитании чисел принадлежащих разным множествам необходимо произвести расширение числа из множества с меньшей мощностью в сторону числа из множества с большей мощностью, либо оба числа расширить до уравнивания множеств, если существует такая возможность. Например, если нужно вычесть из рационального числа натуральное число , то воспользовавшись тем, что натуральные числа являются подмножеством рациональных, расширяем натуральное число до рационального числа и вычитаем два рациональных числа . Аналогично, пользуясь тем, что: можно вычитать числа из различных множеств между собой.
Особенности обучения вычитанию школьников[править | править код]
Практика показывает, что школьников легче научить вычислять разность чисел, чем научить их принимать решение о применимости операции вычитания в той или иной задаче. Это связано с тем, что вычитание, в отличие, например, от сложения, — некоммутативная операция, её аргументы играют разные роли, и ситуации задач на вычитание, которые должен разрешить ученик, существенно разнообразней, чем при сложении. В связи с этим детям, решившим задачу на вычитание одного вида, может быть затруднительно решить задачу на вычитание другого вида, даже с такими же числовыми данными. Педагог, работающий с ребёнком, должен убедиться, что его ученик уверенно чувствует себя и находит решение задач на вычитание следующих видов:
| Виды задач | Примеры задач |
| Задачи на нахождение результата действия или процесса, приводящих к уменьшению (расходу) начального количества | У Васи было 5 яблок, 3 из них он раздал друзьям. Сколько яблок у него осталось? |
| Задачи на сравнение чисел и величин, нахождение разницы, превышения, избытка | На участке дороги максимальная разрешённая скорость — 60 км/ч. Автомобиль едет по ней со скоростью 85 км/ч. На сколько водитель превышает допустимую скорость? |
| Задачи на измерение интервалов — временных и пространственных (как особый cлучай предыдущего вида задач) | В школе уроки заканчиваются в 13 часов 05 минут. Сейчас 10 часов 42 минуты. Сколько ещё ждать до конца уроков? |
| Задачи на нахождение неизвестной части совокупности (объёма) как дополнения к известной части. | В классе 25 учеников. У двоих из них — рыжий цвет волос, у восьми — каштановый, шестеро — блондинов, остальные — брюнеты. Сколько в классе брюнетов? |
| Задачи на обращение операции сложения. Восстановление первого операнда | Маша положила в копилку 25 рублей и всего у неё стало 583 рубля. Сколько денег было у Маши до этого? |
| Задачи на обращение операции сложения. Восстановление второго операнда | Одна ручка стоит 20 рублей, а ручка и блокнот стоят 50 рублей. Сколько стоит блокнот? |
| Задачи на обращение операции вычитания. Восстановление второго операнда (вычитаемого) | На дереве сидело 16 ворон. Несколько ворон улетело, а осталось 5. Сколько ворон улетело? |
См. также[править | править код]
- Сумма
- Сложение
- Умножение
- Деление
Примечания[править | править код]
- ↑ Вычитание // Математическая энциклопедия. М.: Советская энциклопедия, 1977—1985.
- ↑ Subtraction (англ.) на сайте PlanetMath.
- ↑ Лебедев, 2003, с. 97.
- ↑ Так эти свойства называются в учебниках для младших классов
- ↑ Истомина, 2005, с. 165.
- ↑ Выгодский, 2003.
- ↑ Гусев, 1988, с. 20.
- ↑ Поскольку на множестве вещественных чисел уже введено отношение линейного порядка, то мы можем определить топологию числовой прямой: в качестве открытых множеств возьмём всевозможные объединения интервалов вида
- ↑ Ильин, 1985, с. 46.
- ↑ Конвей, 1986, с. 107.
Литература[править | править код]
- Ильин В.А. и др. Математический анализ. Начальный курс. (неопр.). — МГУ, 1985. — Т. 1. — 662 с.
- Эндертон Г. Элементы теории множеств = Elements of Set Theory. — Gulf Professional Publishing, 1977. — 279 с. — ISBN 0-12-238440-7.
- Барсуков А.Н. Алгебра. Учебник для 6-8 классов. (неопр.). — Просвещение, 1966. — 296 с.
- Гусев В.А., Мордкович А.Г. Математика. Справочные материалы, книга для учащихся. (неопр.). — Просвещение, 1988. — 416 с.
- Истомина Н.Б. Методика обучения математике в начальной школе: Развивающее обучение. (неопр.). — Ассоциация XXI век, 2005. — 272 с. — ISBN 5-89308-193-5.
- Выгодский М. Я. Справочник по элементарной математике (неопр.). — М.: АСТ, 2003. — ISBN 5-17-009554-6.
- В.И. Игошин. КУРС ЧИСЛОВЫХ СИСТЕМ ДЛЯ ПЕДАГОГИЧЕСКОГО ВУЗА (рус.) : статья. — Саратовский государственный университет имени Н.Г. Чернышевского, 2010.
- Кононюк А.Е. Обобщенная теория моделирования. (неопр.). — Освіта України, 2012. — Т. 2. — 548 с. — ISBN 978-966-7599-50-8.
- Тире, минус и дефис, или Черты русской типографики : [арх. 24 августа 2011] // Ководство / Артемий Лебедев. — 2003. — § 97 (15 января).
- Conway, John B. Функция одной комплексной переменной = Functions of One Complex Variable I. — Springer Science, 1986. — 322 с. — ISBN 0-387-90328-3.
