Какая величина характеризует инертные свойства тела при вращательном движении
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 8 апреля 2020;
проверки требует 1 правка.
Враща́тельное движе́ние — вид механического движения. При вращательном движении материальная точка описывает окружность. При вращательном движении абсолютно твёрдого тела все его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружностей и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения в данной системе отсчёта может быть как подвижной, так и неподвижной. Например, в системе отсчёта, связанной с Землёй, ось вращения ротора генератора на электростанции неподвижна.
При выборе некоторых осей вращения, можно получить сложное вращательное движение — сферическое движение, когда точки тела движутся по сферам. При вращении вокруг неподвижной оси, не проходящей через центр тела или вращающуюся материальную точку, вращательное движение называется круговым.
Основной закон динамики вращательного движения[править | править код]
Производная по времени от момента количества движения механической системы относительно неподвижной инерциальной системы отсчёта точки или центра инерции системы равна главному моменту относительно той же точки всех внешних сил, приложенных к системе.
Характеристики вращения тела[править | править код]
Кинематические характеристики[править | править код]
Вращение характеризуется углом , измеряющимся в градусах или радианах, угловой скоростью (измеряется в рад/с) и угловым ускорением (единица измерения — рад/с²).
При равномерном вращении ( — период вращения),
- Частота вращения — число оборотов в единицу времени.
- Линейная скорость точки, находящейся на расстоянии от оси вращения
- Угловая скорость вращения тела — аксиальный вектор (псевдовектор).
Динамические характеристики[править | править код]
Свойства твердого тела при его вращении описываются моментом инерции твёрдого тела. Эта характеристика входит в дифференциальные уравнения, полученные из уравнений Гамильтона или Лагранжа. Кинетическую энергию вращения можно записать в виде:
В этой формуле момент инерции играет роль массы, а угловая скорость — роль скорости. Момент инерции выражает геометрическое распределение массы в теле и может быть найден из формулы
- Момент инерции — физическая величина, мера инертности тела во вращательном движении. Характеризует распределение масс в теле. Различают осевой и центробежный момент инерции. Осевой момент инерции определяется равенством:
где — масса, — расстояние от -й точки до оси[1].
См. также[править | править код]
- Поступательное движение
- Плоскопараллельное движение
- Сложное движение
- Сферическое движение
Примечания[править | править код]
- ↑ Момент инерции // Физическая энциклопедия. В 5-ти томах / Главный редактор А. М. Прохоров. — М.: Советская энциклопедия, 1988.
Ссылки[править | править код]
- Бобылёв Д. К. Ось, в математике, механике и физике // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
- Вращение твердого тела. Открытая Физика 2.6. Часть I. «ФИЗИКОН». Дата обращения 23 января 2015.
- Джанибеков демонстрирует пример вращения абсолютно жесткого тела, закрученного вокруг оси, не совпадающей с осью наименьшего или наибольшего момента инерции
- Вращение твёрдых тел в невесомости вокруг разных осей
- Б. Яворский А. Детлаф, Физика, М.: Дрофа, 1998.
Анонимный вопрос · 7 декабря 2018
3,3 K
Для характеристики инертности тела в поступательном движении введена инерционная масса (скалярная величина).
Для характеристик инертности тела во вращательных движениях введены моменты инерции (скалярные величины):
- осевой момент инерции,
- центробежный момент инерции,
- геометрические моменты инерции,
- момент инерции относительно плоскости,
- центральный момент инерции,
а также тензор инерции (тензорная величина).
Для характеристики способности тела участвовать в гравитационном взаимодействии введена гравитационная масса (скалярная величина).
В химии газы, ранее известны как инертные из-за предполагаемого отсутствия участия в каких-либо химических реакциях, были переименованы в благородные газы, так как стало известно, что эти газы реагируют с образованием химических соединений, например, тетрафторида ксенона.
Термин «инертный» также может быть применён в относительном смысле, как «не реакционно-способный».
Мои интересы: разнообразны, но можно выделить следующие: литература, история…
Для характеристики инертности тела введена такая величина, как масса, чем она больше, тем выше инертность, то есть больше времени потребуется телу для совершения движения.
Почему потенциальная энергия всегда стремится к нулю?
Аспирант Принстона, выпускник кафедры физики частиц и космологии МГУ
Правильнее было бы сказать к минимуму. Полная энергия в системе сохраняется. Возьмем механическую систему с трением, полная энергия состоит из 3 частей: кинетическая, потенциальная и тепловая. Первые два вида — механическая энергия, переходят в третью только в результате движения, а тепловая энергия наоборот самопроизвольно не может переходить в кинетическую и потенциальную, это противоречит 2 началу термодинамики. Поэтому механическая энергия всегда уменьшается если есть движение и трение, так будет пока тело не остановится.
Допустим движения нет, и мы находимся не в минимуме потенциальной энергии, тогда потенциальная энергия может перейти в кинетическую, и тело начнет двигаться. В результате механическая энергия снова будет переходить в тепловую. Так может продолжаться до тех пор, пока лишней потенциальной энергии не останется и тело при этом не остановится, то есть пока потенциальная энергия не достигнет минимума, а кинетическая нуля.
Прочитать ещё 1 ответ
Что характеризует сила?
младший научный сотрудник ФТИ им. Иоффе
сила в физике — мера воздействия на данное тело со стороны других тел или полей. Величина и направление силы определяют изменение скорости тела. Выражается это вторым законом Ньютона — масса тела, умноженная на ускорение равняется действующей на тело силе. Измеряется сила в ньютонах, Один ньютон — такая сила, под действием которой тело с массой 1 килограмм ускоряется на 1 метр в секунду за 1 секунду
Как учёные обнаружили, что скорость света — предел?
Все слышали про общую теорию относительности, и все примерно представляют себе ее тезисы. Вспомним один из них.
Время относительно. Это буквально означает, что если двигаться мимо совершенно точных и исправных часов (с любой скоростью), они покажутся вам идущими медленно. Одна секунда на них будет длиться для вас дольше секунды — тем дольше, чем быстрее вы двигаетесь. Но та же одна секунда этих часов будет длиться ровно одну секунду для того, кто в этот момент просто стоит возле них.
То же происходит с пространством. Если вы двигаетесь навстречу шару и каким-нибудь образом успеете на ходу измерить его диаметр, выставив линейку по направлению движения, окажется, что шар для вас стал сплюснутым. Да, верно: тем более сплюснутым, чем быстрее вы двигаетесь.
И вот мы двигаемся все быстрее. Еще быстрее, еще быстрее. Шары на нашем пути сплющиваются, часы на нашем пути замедляются. Они делают это с экспоненциальной скоростью: сначала чтобы заметить разницу нужно разогнаться очень сильно, чуть позже уже малейший прирост в скорости будет давать заметный невооруженным взглядом эффект сжатия. И так до тех пор, пока… пока все шары вокруг вас не станут дисками нулевой толщины с нулевым расстоянием между ними. Пока все часы не остановятся. Расстояние до любого объекта впереди или позади будет равно нулю, секунда на чужих часах будет длиться бесконечно. С вашей точки зрения вы будете находиться во всех точках своей траектории одновременно, а понятие времени или изменения просто исчезнет. Прошлое и будущее, равно как направления «вперед» и «назад» перестанут иметь для вас смысл.
Конечно, сделать этого вы не сможете, потому что у вас есть масса: вы сможете бесконечно приближаться к этой границе, но никогда не достигнете ее. Это асимптота на графиках восприятия пространства и времени. Но у света массы нет, и для него те же графики совпадают с асимптотами.
Строго говоря, называть эту скорость «скоростью света» не совсем точно. Это предел кривизны пространства и времени. Что угодно, не имеющее массы, окажется именно в этом пределе. Свету повезло быть именно такой сущностью, но с тем же успехом мы могли бы назвать эту величину «скоростью немассивных тел».
Свет движется с этой скоростью, потому что у него нет массы, а не сама скорость стала максимальной благодаря свету. Забудьте про свет. Представьте себе, каково быть объектом без массы, для которого перестало существовать время и пространство. Скорость — это расстояние, проходимое в единицу времени. Как можно развить скорость еще выше, когда расстояния и времени для вас уже не существует?
Прочитать ещё 5 ответов
Информация обладает энергией или энергия обладает информацией ?
Рассуждаем логически: любая информация несёт в себе энергию, просматривая фильмы различных жанров вы насыщаетесь энергией радости, любви, ужаса, эротики, и так далее, в зависимости от жанра, замысла режиссера и способа воплощения картины командой профессионалов. С другой стороны, информация это скорее разновидность энергии, которая сама по себе является более общим понятием и способна принимать бесчисленное количество форм, включая информационную. Следовательно , всякая информация это энергия, но не всякая энергия — это информация. Одно и то же энергетическое явление будет нести совершенно различный смысл воспринимающему его субъекту , в зависимости от происхождения, вида и миллиона прочих параметров, а для оных и вообще будет лишено всякого информационного смысла, но не перестанет от этого быть энергией.
Прочитать ещё 1 ответ
В этой статье описывается важный раздел физики — «Кинематика и динамика вращательного движения».
Основные понятия кинематики вращательного движения
Вращательным движением материальной точки вокруг неподвижной оси называют такое движение, траекторией которого является окружность, находящаяся в плоскости перпендикулярной к оси, а центр ее лежит на оси вращения.
Вращательное движение твердого тела — это движение, при котором по концентрическим (центры которых лежат на одной оси) окружностям движутся все точки тела в соответствии с правилом для вращательного движения материальной точки.
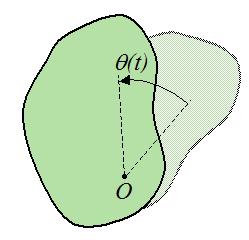
Пусть произвольное твердое тело T совершает вращения вокруг оси O, которая перпендикулярна плоскости рисунка. Выберем на данном теле точку M. При вращении эта точка будет описывать вокруг оси O круг радиусом r.
Через некоторое время радиус повернется относительно исходного положения на угол Δφ.
За положительное направление поворота принято направление правого винта (по часовой стрелке). Изменение угла поворота со временем называется уравнением вращательного движения твердого тела:
φ = φ(t).
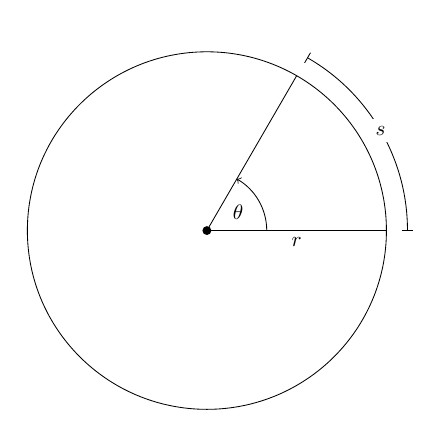
Если φ измерять в радианах (1 рад — это угол, соответствующий дуге, длиной равной ее радиусу), то длина дуги окружности ΔS, которую пройдет материальная точка M за время Δt, равна:
ΔS = Δφr.
Основные элементы кинематики равномерного вращательного движения
Мерой перемещения материальной точки за небольшой промежуток времени dt служит вектор элементарного поворота dφ.
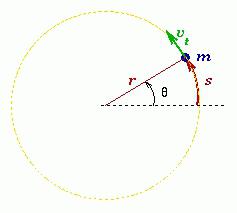
Угловая скорость материальной точки или тела — это физическая величина, которая определяется отношением вектора элементарного поворота к продолжительности этого поворота. Направление вектора можно определить правилом правого винта вдоль оси О. В скалярном виде:
ω = dφ/dt.
Если ω = dφ/dt = const, то такое движение называется равномерное вращательное движение. При нем угловую скорость определяют по формуле
ω = φ/t.
Согласно предварительной формуле размерность угловой скорости
[ω] = 1 рад/с.
Равномерное вращательное движение тела можно описать периодом вращения. Период вращения T — физическая величина, определяющая время, за которое тело вокруг оси вращения выполняет один полный оборот ([T] = 1 с). Если в формуле для угловой скорости принять t = T, φ = 2 π (полный один оборот радиуса r), то
ω = 2π/T,
поэтому период вращения определим следующим образом:
T = 2π/ω.
Число оборотов, которое за единицу времени совершает тело, называется частотой вращения ν, которая равна:
ν = 1/T.
Единицы измерения частоты: [ν]= 1/c = 1 c-1 = 1 Гц.
Сравнивая формулы для угловой скорости и частоты вращения, получим выражение, связывающее эти величины:
ω = 2πν.
Основные элементы кинематики неравномерного вращательного движения
Неравномерное вращательное движение твердого тела или материальной точки вокруг неподвижной оси характеризует его угловая скорость, которая изменяется со временем.
Вектор ε, характеризующий скорость изменения угловой скорости, называется вектором углового ускорения:
ε = dω/dt.

Если тело вращается, ускоряясь, то есть dω/dt > 0, вектор имеет направление вдоль оси в ту же сторону, что и ω.
Если вращательное движение замедлено — dω/dt < 0, то векторы ε и ω противоположно направлены.
Замечание. Когда происходит неравномерное вращательное движение, вектор ω может меняться не только по величине, но и по направлению (при повороте оси вращения).
Связь величин, характеризующих поступательное и вращательное движение
Известно, что длина дуги с углом поворота радиуса и его величиной связана соотношением
ΔS = Δφ r.
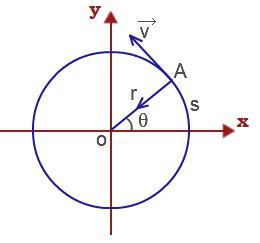
Тогда линейная скорость материальной точки, выполняющей вращательное движение
υ = ΔS/Δt = Δφr/Δt = ωr.
Нормальное ускорение материальной точки, что выполняет вращательно поступательное движение, определим следующим образом:
a = υ2/r = ω2r2/r.
Итак, в скалярном виде
a = ω2r.
Тангенциальное ускоренной материальной точки, которая выполняет вращательное движение
a = ε r.
Момент импульса материальной точки
Векторное произведение радиуса-вектора траектории материальной точки массой mi на ее импульс называется моментом импульса этой точки касательно оси вращения. Направление вектора можно определить, воспользовавшись правилом правого винта.
Момент импульса материальной точки (Li) направлен перпендикулярно плоскости, проведенной через ri и υi, и образует с ними правую тройку векторов (то есть при движении с конца вектора riк υi правый винт покажет направление вектора Li).
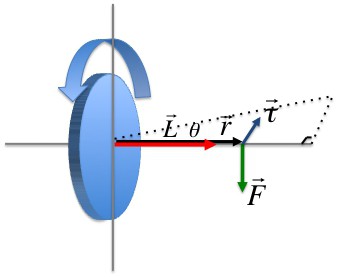
В скалярной форме
L = miυirisin(υi,ri).
Учитывая, что при движении по кругу радиус-вектор и вектор линейной скорости для i-й материальной точки взаимно перпендикулярные,
sin(υi,ri) = 1.
Так что момент импульса материальной точки для вращательного движения примет вид
L = miυiri.
Момент силы, которая действует на i-ю материальную точку
Векторное произведение радиуса-вектора, который проведен в точку приложения силы, на эту силу называется моментом силы, действующей на i-ю материальную точку относительно оси вращения.
В скалярной форме
Mi = riFisin(ri, Fi).
Считая, что risinα = li, Mi = liFi.
Величина li, равная длине перпендикуляра, опущенного из точки вращения на направление действия силы, называется плечом силы Fi.
Динамика вращательного движения
Уравнение динамики вращательного движения записывается так:
M = dL/dt.
Формулировка закона следующая: скорость изменения момента импульса тела, которое совершает вращение вокруг неподвижной оси, равна результирующему моменту относительно этой оси всех внешних сил, приложенных к телу.
Момент импульса и момент инерции
Известно, что для i-й материальной точки момент импульса в скалярной форме задается формулой
Li = miυiri.
Если вместо линейной скорости подставить ее выражение через угловую:
υi = ωri,
то выражение для момента импульса примет вид
Li = miri2ω.
Величина Ii = miri2 называется моментом инерции относительно оси i-й материальной точки абсолютно твердого тела, проходящей через его центр масс. Тогда момент импульса материальной точки запишем:
Li = Iiω.
Момент импульса абсолютно твердого тела запишем как сумму моментов импульса материальных точек, составляющих данное тело:
L = Iω.
Момент силы и момент инерции
Закон вращательного движения гласит:
M = dL/dt.
Известно, что представить момент импульса тела можно через момент инерции:
L = Iω.
Тогда
M = Idω/dt.
Учитывая, что угловое ускорение определяется выражением
ε = dω/dt,
получим формулу для момента силы, представленного через момент инерции:
M = Iε.
Замечание. Момент силы считается положительным, если угловое ускорение, которым он вызван, больше нуля, и наоборот.
Теорема Штейнера. Закон сложения моментов инерции
Если ось вращения тела через центр масс его не проходит, то относительно этой оси можно найти его момент инерции по теореме Штейнера:
I = I0 + ma2,
где I0 — начальный момент инерции тела; m — масса тела; a — расстояние между осями.
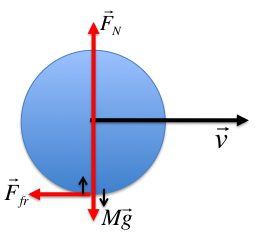
Если система, которая совершает обороты округ неподвижной оси, состоит из n тел, то суммарный момент инерции такого типа системы будет равен сумме моментов, ее составляющих (закон сложения моментов инерции).
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 января 2019;
проверки требуют 5 правок.
Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения в Международной системе единиц (СИ): кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.
Осевой момент инерции[править | править код]
Осевые моменты инерции некоторых тел
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси[1]:
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
где:
dm = ρ dV — масса малого элемента объёма тела dV,
ρ — плотность,
r — расстояние от элемента dV до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса — Штейнера[править | править код]
Момент инерции твёрдого тела относительно какой-либо оси зависит от массы, формы и размеров тела, а также и от положения тела по отношению к этой оси. Согласно теореме Гюйгенса — Штейнера, момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями[1]:
где m — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел[править | править код]
Вывод формул[править | править код]
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобьём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перпендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска.
Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобьём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции шара найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобьём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l⁄2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников[2][3][4]
Безразмерные моменты инерции планет и спутников[править | править код]
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение доплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра[5][6].
Центробежный момент инерции[править | править код]
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины[1][7]:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции данного тела[7].
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции[7].
Геометрические моменты инерции[править | править код]
Геометрический момент инерции объёма относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
где, как и ранее r — расстояние от элемента dV до оси a.
Размерность JVa — длина в пятой степени (), соответственно единица измерения СИ — м5.
Геометрический момент инерции площади относительно оси — геометрическая характеристика тела, выражаемая формулой[8]:
где интегрирование выполняется по поверхности S, а dS — элемент этой поверхности.
Размерность JSa — длина в четвёртой степени (), соответственно единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката часто указывается в см4.
Через геометрический момент инерции площади выражается момент сопротивления сечения:
Здесь rmax — максимальное расстояние от поверхности до оси.
Момент инерции относительно плоскости[править | править код]
Моментом инерции твёрдого тела относительно некоторой плоскости называют скалярную величину, равную сумме произведений массы каждой точки тела на квадрат расстояния от этой точки до рассматриваемой плоскости[9].
Если через произвольную точку провести координатные оси , то моменты инерции относительно координатных плоскостей , и будут выражаться формулами:
В случае сплошного тела суммирование заменяется интегрированием.
Центральный момент инерции[править | править код]
Центральный момент инерции (момент инерции относительно точки O, момент инерции относительно полюса, полярный момент инерции) — это величина, определяемая выражением[9]:
где:
Центральный момент инерции можно выразить через главные осевые моменты инерции, а также через моменты инерции относительно плоскостей[9]:
Тензор инерции и эллипсоид инерции[править | править код]
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
(1)
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также[править | править код]
Комментарии[править | править код]
- ↑ В правильности использования знака «+» в этой формуле можно убедиться, если сравнить моменты инерции полого толстостенного и сплошного цилиндров с одинаковыми массами. Действительно, у первого из этих цилиндров масса в среднем сосредоточена дальше от оси, чем у второго, поэтому и момент инерции этого цилиндра должен быть больше, чем у сплошного. Именно такое соотношение моментов инерции и обеспечивает знак «+». С другой стороны, в пределе при стремлении r1 к r2 формула для полого толстостенного цилиндра должна приобрести тот же вид, что и формула для полого тонкостенного цилиндра. Очевидно, что такой переход происходит только при использовании формулы со знаком «+».
Примечания[править | править код]
Литература[править | править код]
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.)
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997.
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с.
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с.
- Беляев Н. М. Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки[править | править код]
- Определение момента инерции тел простой формы.
