Какая из операций над множествами не обладает свойством симметрии

План лекции:

1) Пересечение множеств.

2) Объединение множеств.

3) Разность множеств.

4) Симметрическая разность.

5) Дополнение множеств.

6) Декартово (прямое) произведение двух множеств.

1. Пересечением множеств А и В называется множество, состоящее из элементов, которые принадлежат множествам А и В одновременно.

Пересечение множеств А и В обозначают: А Ç В.

А Ç В = {х| хÎА и хÎВ}

Если представить множества А и Впри помощи кругов Эйлера, то пересечение данных множеств изобразится заштрихованной областью (рис. 1).

В том случае, когда множества А и В не имеют общих элементов, то говорят, что их пересечение пусто и пишут: А Ç В = Æ.

А Ç Æ = Æ.

Если ВÌ А, то А Ç В = В.

Операция, при помощи которой находят пересечение множеств, называется также пересечением.

Пример.

1) А ={1, 2, 3, 4, 5}; В = {4, 5, 6, 7}

А Ç В = {4, 5}

2) Пересечением множества прямоугольников и множества ромбов является множество квадратов.

3) Пересечением множества чётных чисел и множества нечётных чисел пусто.

2. Объединением множеств А и В называется множество, состоящее из элементов, которые принадлежат хотя бы одному из множеств А и В.

Объединение множеств А и В обозначают: А È В.

А È В = {х| хÎА или хÎВ}

Если представить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится заштрихованной областью (рис. 2).

Если ВÌ А, то А È В = А.

А È Æ = А.

Операция, при помощи которой находят объединение множеств, называется также объединением.

Пример.

1) А = {1, 2, 3, 4, 5}; В = {4, 5, 6, 7}

А È В = {1, 2, 3, 4, 5, 6, 7}

2) Объединение множества положительных чётных чисел и множества положительных нечётных чисел является множество натуральных чисел.

Если в выражении есть Ç и È множеств, но нет скобок, то сначала выполняют Ç.

Операции пересечения и объединения множеств обладают свойствами:

1° Коммутативность пересечения

«А, В А Ç В = В Ç А

2° Коммутативность объединения

«А, В А È В = В È А

3º Ассоциативность пересечения

«А, В, С (А Ç В) Ç С = А Ç (В Ç С)

4º Ассоциативность объединения

«А, В, С (А È В) È С = А È (В È С)

5º Пересечение дистрибутивно относительно объединения

«А, В, С А Ç (В È С) = (А Ç В) È (А Ç С)

6º Объединение дистрибутивно относительно пересечения

«А, В, С А È (В Ç С) = (А È В) Ç (А È С)

7º «А А Ç А = А

8º «А А È А = А

Доказательство:

Справедливость каждого из этих утверждений можно проверить, показав, что множество, стоящее по одну сторону от знака равенства, включено в множество, стоящее по другую сторону от этого знака.

Например, докажем свойство 6º.

а) Докажем, что А È (В Ç С) Ì (А È В) Ç (А È С).

Пусть х Î А È (В Ç С). Тогда х Î А или х Î (В Ç С).

Если х Î А, то х Î А È В и х Î А È С, а, следовательно, х Î (А È В) Ç (А È С).

Если х Î (В Ç С), то х Î В и х Î С. Следовательно, х Î А È В и х Î А È С, т.е. и в этом случае х Î (А È В) Ç (А È С).

б) Докажем, что (А È В) Ç (А È С) Ì А È (В Ç С).

Пусть х Î (А È В) Ç (А È С). Тогда х Î А È В и х Î А È С.

То есть, (х Î А или х Î В) и (х Î А или х Î С).

Значит, х Î А или (х Î В и х Î С), т.е. х Î А È (В Ç С).

Проиллюстрируем свойство 6º на диаграммах Эйлера–Венна.

3. Разностью множеств А и В называется множество, элементы которого принадлежат множеству А и не принадлежат множеству В.

Обозначают А В; А – В.

А В = { х| хÎА и хÏВ }

Если представить множества А и В при помощи кругов Эйлера, то разность данных множеств изобразится заштрихованной областью (рис. 3).

Операция, при помощи которой находят разность множеств, называется вычитанием.

Пример.

1) А = {1, 2, 3, 4, 5}; В = {4, 5, 6, 7}

А В = {1, 2, 3}

2) Разностью множества чётных чисел и множества целых чисел является пустое множество.

4. Симметрической разностью множеств А и В называется множество, состоящее из элементов, принадлежащих только множеству А или только множеству В.

Симметрическую разность множеств А и В обозначают: А х В; А – В.

А х В = { х| хÎА, хÏВ или хÏА, хÎВ}

Если представить множества А и В при помощи кругов Эйлера, то симметрическая разность данных множеств изобразится заштрихованной областью (рис. 4).

А х В = (А В) È (В А)

А х В = (А È В) (А Ç В)

5. Универсальным множеством U (основным множеством) называется множество, для которого все множества, рассматриваемые в данный момент, являются подмножествами.

Универсальное множество часто изображают прямоугольником.

Например, для N универсальным считается множество Z.

Дополнением множества А называется разность между универсальным множеством и множеством А.

Дополнение множества А обозначают .

= U A = {хÏА}

При помощи кругов Эйлера дополнение изображается рис. 5.

È А = U = Æ

Ç А = Æ = U

Пример.

1) А = {2k}; U = Z ® = Z A = {2k+1}.

Операции разности и дополнения множеств обладают свойствами:

9º Разность антидистрибутивна относительно пересечения. «А, В, С

А (В Ç С) = (А B) È (A C)

10º Разность антидистрибутивна относительно объединения. «А, В, С

А (В È С) = (А B) Ç (A C)

11º (частный сл. 9º) Дополнение пересечения А и В равно объединению дополнений А и В.

12º (частный сл. 10º) Дополнение объединения А и В равно пересечению дополнений А и В.

Докажем св. 9º и проиллюстрируем его на диаграммах Эйлера–Венна.

а) Докажем, что А (В Ç С) Ì (А B) È (A C).

Пусть х Î А (В Ç С).

Тогда х Î А и х Ï (В Ç С), т.е. или х Ï В, или х Ï С.

Значит, или (х Î А и х Ï В), или (х Î А и х Ï С), т.е. х Î А B или хÎА С.

Т.е. х Î(А B) È (A C).

б) Докажем, что (А B) È (A C) Ì А (В Ç С).

Пусть х Î (А B) È (A C).

Тогда х Î (А B) или х Î (A C), т.е. (х Î А и х Ï В) или (х Î А и х Ï С)

Значит, х Î А и (х Ï В и х Ï С), т.е. х Î А (В Ç С).

Дом. задание. Доказать и проиллюстрировать на диаграммах Эйлера–Венна свойства 1 – 5, 7 – 12.

Задание. Найти пересечение, объединение, разность и симметрическую разность множеств А и В, если А = {хÎR ½–1£ х < 4}, B = { хÎR ½ 2 < x £ 6}

А Ç В = {хÎR ½2 < x < 4},

А È В = {хÎR ½–1 £ x £ 6},

А B = {хÎR ½–1 £ x £ 2},

В А = {хÎR ½4 £ x £ 6},

А ? В = {хÎR ½–1 £ x < 2, 4 < x £ 6}.

Источник

Множество – определенная совокупность объектов.

Объекты, из которых состоит множество, называются элементами множества.

ПРИМЕР

Множество домов на данной улице, множество натуральных чисел, множество студентов группы и т. д.

Множества обычно обозначают заглавными латинскими буквами А, В, С, D, X, Y…, элементы множества строчными латинскими буквами – a, b, c, d, x, y…

Для обозначения того, что объект x является элементом множества A, используют символику: xА (читается: x принадлежит А ), запись xА обозначает, что объект x не является элементом множества A (читается: x не принадлежит А).

Множество не содержащее ни одного элемента называется пустым (обозначается: Ø).

Множества из элементов которого составляем конкретное множество называется универсальным (обозначается: U).

ПРИМЕР

U – множество людей на земле, А – студенты группы Эп-305.

Множества можно изображать с помощью кругов, которые называются кругами Эйлера или диаграммами Венна, универсальное множество принято обозначать прямоугольником.

ПРИМЕР

Тема 2.2. Способы задания множеств

Чтобы задать множество, нужно указать, какие элементы ему принадлежат. Это можно сделать различными способами:

1) Перечислением всех элементов множества в фигурных скобках.

ПРИМЕР

A = {Оля, Маша, Саша}

2) Характеристическим предикатом, который описывает свойство всех элементов, входящих в множество. Характеристический предикат записывается после двоеточия или символа « | ».

ПРИМЕР

Р(x) = xN x < 8 — характеристический предикат.

M = {x : Р(x)} или M = {x : xN x < 8}.

Множество M можно задать и перечислением его элементов:

M = {1, 2, 3, 4, 5, 6, 7}

ПРИМЕР

В = {x | x — четное натуральное число} = {2, 4, 6, 8, …}

Если множество состоит из небольшого количества элементов, то его удобно задавать перечислением всех элементов, если же элементов много или множество имеет бесконечное число элементов, то оно задается с помощью характеристического предиката.

Тема 2.3. Операции над множествами

1) Сравнение множеств

Множество А называется подмножеством множества В, если все элементы множества А содержатся во множестве В.

Два множества называются равными, если они содержат одинаковые наборы элементов.

ТЕОРЕМА

# Пустое множество Ø является подмножеством всех множеств.

# Универсальное множество U содержит все множества.

# Если , то В надмножество А.

ПРИМЕР

А={0, 1, 2, 3}, В={0, 1}, .

2) Объединением двух множеств называется множество, содержащее все элементы обоих множеств.

ПРИМЕР

А={К, А, Т, Я}, В={К, О, С, Т, Я},

3) Пересечением двух множеств называется множество, состоящее из общих элементов обоих множеств.

ПРИМЕР

А={К, А, Т, Я}, В={К, О, С, Т, Я}, ={К, Т, Я}.

4) Разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В.

ПРИМЕР

А={К, А, Т, Я}, В={К, О, С, Т, Я}, А В={A}, В А ={О, С}.

5) Симметрической разностью множеств А и В называется множество, состоящее из всех элементов множества А не содержащихся в В и всех элементов множества В не содержащихся в А.

ПРИМЕР

А={К, А, Т, Я}, В={К, О, С, Т, Я}, А Δ В={A,О,С}.

6) Дополнением (дополнением до универсального множества) множества А называется множество, состоящее из всех элементов универсального множества не содержащихся в А.

7) Прямым или декартовым произведением множеств A и B, называется множество всех упорядоченных пар (a, b), где первый элемент a из множества A, а второй элемент b из множестваB.

ПРИМЕР

Степенью множества называется декартовое произведение множества A само на себя n раз.

ПРИМЕР

, .

Свойства операций над множествами

1) Коммутативность.

2) Ассоциативность.

3) Дистрибутивность.

4) Закон поглощения.

5) Идемпотентность.

6) Инволютивность.

7) Свойство нуля.

АØ=А

АØ= Ø

8) Свойство единицы.

9) Закон де Моргана

Мощность множества

Мощностью конечного множества называется число его элементов.

Мощность множества X обозначается: | X |

ПРИМЕР

X ={1,3,6},

| X | = 3

Источник

1.1. Множества и отношения. Множества и элементы множеств
1.2. Сравнение множеств
1.3. Операции над множествами
1.4. Диаграммы Эйлера-Венна
1.5. Табличный способ задания множеств
1.6. Свойства операций над множествами
1.7. Отношения
1.8. Специальные бинарные отношения

1.1. Множества и отношения

Множества и элементы множеств

Определение. Множество – любая определенная совокупность объектов произвольной природы. Обозначают множества прописными латинскими буквами: A, B, ¼ , а его элементы обозначаются строчными латинскими буквами: a, b, ¼.

Например:

( является элементом множества (» принадлежит A«)),

( не является элементом множества A).

Определение. Пустое множество – это множество, не содержащее ни одного элемента, обозначается оно символом: Æ.

Определение. – универсальное множество (универсум) – множество, из которого берутся элементы в конкретном рассуждении. – множество, рассматриваемое как наиболее общее в данной ситуации.

Множество элементов , удовлетворяющих свойству P(x) обозначается .

Примеры.

– множество натуральных чисел;

– множество вещественных чисел.

– множество комплексных чисел.

1.2. Сравнение множеств

Определение. (А содержится в В или В включает А), если . А называется подмножеством В. Если и , то А называется строгим (собственным) подмножеством В. Обозначается это .

Определение. если они являются подмножествами друг друга, то есть или

Определение. Мощность конечного множества – число его элементов. Мощность бесконечного множества равна ¥.

1.3. Операции над множествами

Определение. Объединением множеств А и В () называется множество, состоящее из элементов, принадлежащих хотя бы одному из них.

Определение. Пересечением множеств А и В () называется множество, состоящее из элементов, принадлежащих и первому и второму одновременно.

Определение. Разностью множеств А и В () называется множество, состоящее из элементов множества А, не принадлежащих множеству В.

Определение. Симметрической разностью множеств А и В () называется множество, состоящее из элементов множества А, не являющихся элементами множества В и элементов множества В, не являющихся элементами множества А.

Определение. Дополнением множества А () называется множество, состоящее из элементов множества U, не принадлежащих множеству А.

Пример:

зависит от того, какое U. Если , то , если , то .

1.4. Диаграммы Эйлера-Венна

Диаграммы Эйлера-Венна – это геометрическое представление множеств. Множество U изображается прямоугольником, рассматриваемые множества – фигурами (окружностями). Для выделения результата применяется штриховка.

1.5. Табличный способ задания множеств

Пусть задано множество U. Рассмотрим произвольное его подмножество и элемент .

Определение. Индикаторной (характеристической) функцией для множества A называется функция
.

Таким образом: .

Для имеют место свойства:

;

Индикаторы удобно задавать с помощью таблиц:

1.6. Свойства операций над множествами

Объединение и пересечение:

1. = – коммутативность

2. = – коммутативность

3. – ассоциативность

4. – ассоциативность

5. – дистрибутивность

6. – дистрибутивность

7. – идемпотентность

8. – идемпотентность

9. – свойство дополнения

10. – свойство дополнения

11. – закон де Моргана

12. – закон де Моргана

13. – свойство нуля

14. – свойство нуля

Дополнение:

15. – инволютивность

16.

17.

Разность, симметрическая разность:

18.

19.

20.

21.

22.

23.

1.7. Отношения

Определение. Пусть A и B произвольные множества. Декартовым произведением множеств A и B называется множество всевозможных упорядоченных пар, в которых первый элемент принадлежит множеству A, а второй – множеству B.

Пример. – точки плоскости.

Свойства декартовых произведений

Понятие отношения.

Отношение это один из способов задания взаимосвязей между элементами множества.

Унарные (одноместные) отношения отражают наличие какого-либо признака R у элемента множества A. Например, «быть четным» на множестве натуральных чисел. Все элементы множества A, отличающиеся признаком R , образуют подмножество множества A, называемое отношением R.

Бинарные отношения

Бинарные (двуместные) отношения используются для определения взаимосвязей, которыми характеризуются пары элементов множеств A и B. Все пары элементов множеств A и B, находящиеся в отношении R , образуют подмножество множества .

Определение. Бинарное отношение – это тройка множеств , где – график отношения. Пишут или aRb.

Область определения : ;

Область значений: ;

Обратное отношение: ;

Композиция отношений и :

Частичным порядком (пишут ), если оно рефлексивно, антисимметрично и транзитивно.

1.8. Специальные бинарные отношения

Бинарное отношение на A называется

Рефлексивным, если ;
Симметричным, если ;
Транзитивным, если ;
Антисимметричным, если ;
Отношением эквивалентности на (пишут ), если оно рефлексивно, симметрично и транзитивно;

Определение. Бинарное отношение называется функцией из в , если и .

Функция называется

Сюръективной, если ;
инъективной, если ;
биективной, если она сюръективна и инъективна.

Источник

Пересечение и объединение множеств
обладают, коммутативнымсвойством:
для любых множествА,Ввыполняются
равенства:АВ=ВА;АВ=ВА.
Это следует из того, что в определениях
пересечения и объединения множеств
не фиксируется порядок оперирования
множествами. Например, выполняя
объединение, можно к элементам одного
множества присоединить элементы другого,
а можно поступить наоборот: к элементам
второго множества присоединить элементы
первого.

Разность множеств не обладает
коммутативнымсвойством. Это видно
из диаграммы:

АВ

ВА

Какая из операций над множествами не обладает свойством симметрии

Пересечение и объединение множеств
обладают также ассоциативнымсвойством: для любых множествА,ВиСвыполняются равенства:

(АВ)С=А(ВС);
(АВ)С=А(ВС).

Например для пересечения это можно
проиллюстрировать на диаграмме, выполняя
операции в той последовательности,
которая определена скобками.

Какая из операций над множествами не обладает свойством симметрии

АВ

(АВ)
С

ВС

А(ВС)

Разность множеств не обладает
ассоциативнымсвойством. Это видно
из диаграммы:

(АВ)С

А(ВС)

Какая из операций над множествами не обладает свойством симметрии

Задание:
для каких множеств А, В, и С справедливо
равенство: (АВ)С= А(ВС)?

Однако, на
диаграммах можно лишь проиллюстрировать
то или иное свойство операций на
множествах. Для строгого доказательства
этих свойств необходимо рассмотреть
все случаи взаимоотношений между
множествами. Это не сложно, когда речь
идет о двух множествах, но достаточно
трудоемко уже для трех.

Рассмотрим аналитическое доказательство
свойства ассоциативности одной из
операций над множествами, например
объединения, т.е. докажем, что для любых
множеств А, Ви С справедливо равенство
(АВ)С=А(ВС).

Доказательство.
Вспомним определение равенства множеств.
Чтобы доказать равенство двух множеств,
надо убедиться в том, что каждый элемент
множества АВ)
С
содержится в множестве А(ВС),
и наоборот каждый элемент множества
А(ВС)
содержится в множестве АВ)
С.
Таким образом доказательство будет
состоять их двух частей.

1 часть.
Пусть х –
любой элемент множества (АВ)
С,
тогда, по определению объединения х
принадлежит хотя бы одному из объединяемых
множеств, то есть х

(АВ)
или хС.

Если х

(АВ),
то, по определению объединения, х

А или х
В.

Итак, из того что
х

(АВ)
С
следует, что х принадлежит хотя бы одному
из множеств А, В или С. Рассмотрим все
полученные случаи.

если
х 
А, то, по
определению объединения, х
принадлежит объединению А с любым
другим множеством, то есть х

А(ВС).
если
хВ,
то, по определению объединения, х
принадлежит объединению В с любым
другим множеством, то есть х

ВС.
Из того что х
принадлежит ВС
следует что х принадлежит и объединению
ВС
с любым другим множеством, то есть х 
А(ВС).
если
хС,
то, по определению объединения, х
принадлежит объединению В с любым
другим множеством, то есть х

ВС.
Из того что х
принадлежит ВС
следует что х принадлежит и объединению
ВС
с любым другим множеством, то есть х 
А(ВС).

Из
доказанного видно, что каждый элемент
множества (АВ)С
содержится в множестве А(ВС).

2 часть.
Пусть х –
любой элемент множества А(В
С),
тогда, по определению объединения х
принадлежит хотя бы одному из объединяемых
множеств, то есть х

А
или хВС.

Если х

(ВС),
то, по определению объединения, х

В или хС.

Итак, из того что
х

А(В
С)
следует, что х принадлежит хотя бы одному
из множеств А, В или С. Рассмотрим все
полученные случаи.

если
хА,
то, по определению объединения, х
принадлежит объединению А с любым
другим множеством, то есть х

АВ.
Из того что х
принадлежит АВ
следует что х принадлежит и объединению
АВ
с любым другим множеством, то есть х 
(АВ)С.
если
хВ,
то, по определению объединения, х
принадлежит объединению В с любым
другим множеством, то есть х

АВ.
Из того что х
принадлежит АВ
следует что х принадлежит и объединению
АВ
с любым другим множеством, то есть х 
(АВ)С.
если
хС,
то, по определению объединения, х
принадлежит объединению С с любым
другим множеством, то есть х(АВ)С.

Из
доказанного видно, что каждый элемент
множества А(ВС)
содержится в множестве (АВ)С.
Согласно определению равных множеств
заключаем, что (АВ)С=А(ВС).Свойство
доказано.

Задание: проведите строгое
доказательство ассоциативности операции
объединения: (АВ)
С=А(ВС)

Взаимосвязь пересечения и объединения
и разности множеств отражается в
дистрибутивныхсвойствах этих
операций:

(АВ)С=(АВ)(АС)
–дистрибутивность пересечения
относительно объединения;
(АВ)
С=(АВ)

(АС)
–дистрибутивность объединения
относительно пересечения;
(АВ)С=(АВ)(АС)
–дистрибутивность вычитания
относительно объединения;
(АВ)С=(АВ)(АС)
–дистрибутивность пересечения
относительно вычитания.

Заметим, что если в выражении есть знаки
пересечения и объединения множеств и
нет скобок, то сначала выполняют
пересечение, так как считают, что
пересечение более «сильная» операция,
чем объединение. (Например, умножение
чисел более «сильная» операция чем
сложение) Таким образом можно записать
свойства дистрибутивности сократив
количество скобок:

(АВ)С=АВАС;
АВС=(АВ)(АС)

Проиллюстрируем свойство дистрибутивности
пересечения относительно объединения
((АВ)С=АВАС)
на диаграммах:

АВ

(АВ)С

Какая из операций над множествами не обладает свойством симметрии

АВ

АС

(АВ)(АС)

Задание: Проиллюстрируйте
на диаграммах остальные свойства
дистрибутивности.

Для дополнения множеств справедливы
законы де Моргана:

– дополнение объединения множеств
равно пересечению дополнений этих
множеств;
– дополнение пересечения множеств
равно объединению дополнений этих
множеств.

Докажем
первый закон:

Для
того чтобы доказать что множества равны
необходимо показать:

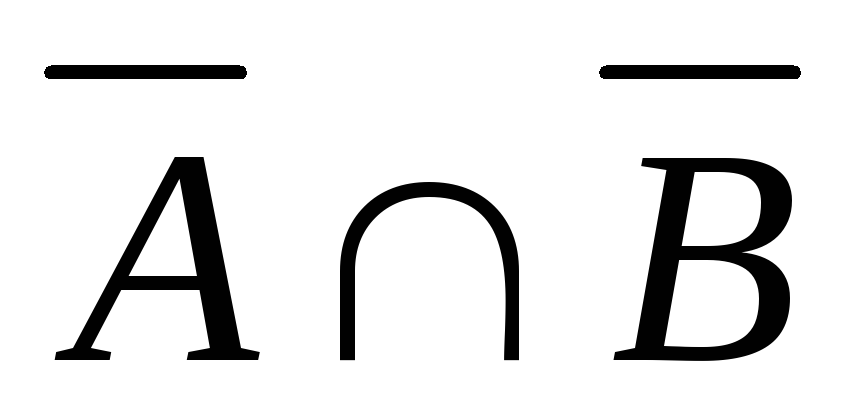является подмножеством;
является подмножеством.

1 часть. Множество
является подмножеством множестваесливсеэлементы множестваявляются так же и элементами множества.

Возьмем произвольный элемент хиз
множества.
Из того чтохследует чтох .
Еслих ,
то это значитх не является элементом
ни множества А, ни множества В, то естьх их .

Так как х не является элементом
множества А, тохявляется элементом
множества.

Так как х не является элементом
множества В, тох является элементом
множества.

Из того что хи одновременнохследует чтох.

Таким образом любой произвольный элемент
хиз множестваявляется также и элементом множества.
Следовательно, множествоявляется подмножеством множества,
что и требовалось доказать в первой
части.