Какая фигура обладает следующими свойствами все углы прямые

- Главная
- Вопросы & Ответы
- Вопрос 7257936
 Гость :
Гость :
1 Июня в 21:24
5
1
Лучший ответ:


Гость :
Квадраттттттттттттттттттттттттттттттттттттт
1 Июня в 21:30
Ваш ответ (не менее 20 символов):
Ваше имя (не менее 2 символов):

Лучшее из галереи:





























Другие вопросы:
 Гость :
Гость :
В синем море…
Прилагательное «синем» в каком падеже?
1 Июня в 21:23
Смотреть ответ
3
1
 Гость :
Гость :
Точки В и D лежат в разных полуплоскостях относительно прямой АС .Треугольники АВС и ADCравнобедренные прямоугольные (угол В и D прямые).Докажет ,что стороны АВ и AD параллельны.
1 Июня в 21:23
Смотреть ответ
5
1
 Гость :
Гость :
Придумай предложения со словами хлопок,гвоздики,кружки,пеньки
1 Июня в 21:22
Смотреть ответ
3
1
 Гость :
Гость :
X + y = z + 1 // z — y = 3 // x = 2•y / найдите решение системы уравнений
1 Июня в 21:22
Смотреть ответ
2
1
 Гость :
Гость :
Из курсов Новейшей истории и обществознания вспомните, что такое постиндустриальное общество? Каковы его особенности?
1 Июня в 21:21
Смотреть ответ
1
0
Многоугольником называется геометрическая фигура, которая со всех сторон ограничена замкнутой ломаной линией. При этом количество звеньев ломаной не должно быть меньше трех. Каждая пара отрезков ломаной имеет общую точку и образует углы. Количество углов совместно с количеством отрезков ломаной являются основными характеристиками многоугольника. В каждом многоугольнике количество звеньев ограничивающей замкнутой ломаной совпадает с количеством углов.
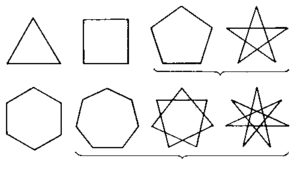
Сторонами в геометрии принято называть звенья ломаной линии, которая ограничивает геометрический объект. Вершинами называют точки соприкосновения двух соседних сторон, по количеству которых получают свои названия многоугольники.
Если замкнутая ломаная состоит из трех отрезков, она носит название треугольника; соответственно, из четырех отрезков — четырехугольником, из пяти — пятиугольником и пр.
Для обозначения треугольника или четырехугольника пользуются заглавными латинскими буквами, обозначающими его вершины. Буквы называют по порядку — по часовой стрелке или против нее.
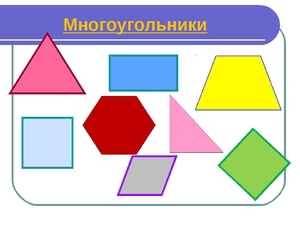
Основные понятия
Описывая определение многоугольника, следует учитывать некоторые смежные геометрические понятия:
- Если вершины являются концами одной стороны, они называются соседними.
- Если отрезок соединяет между собой несоседние вершины, то он имеет название диагонали. У треугольника не может быть диагоналей.
- Внутренний угол — это угол при одной из вершин, который образован двумя его сторонами, сходящимися в этой точке. Он всегда располагается во внутренней области геометрической фигуры. Если многоугольник невыпуклый, его размер может превосходить 180 градусов.
- Внешний угол при определенной вершине — это угол смежный с внутренним при ней же. Иными словами, внешним углом можно считать разность между 180° и величиной внутреннего угла.
- Сумма величин всех отрезков носит название периметра.
- Если все стороны и все углы равны — он носит название правильного. Правильными могут быть только выпуклые.
Как уже упоминалось выше, названия многоугольных геометрических строятся исходя из количества вершин. Если у фигуры их количество равняется n, она носит название n-угольника:
- Многоугольник называется плоским, если ограничивает конечную часть плоскости. Эта геометрическая фигура может быть вписанной в окружность или описанной вокруг окружности.
- Выпуклым называется n-угольник, который соответствует одному из условий, приведенных ниже.
- Фигура расположена по одну сторону от прямой линии, которая соединяет две соседних вершины.
- Эта фигура служит общей частью или пересечением нескольких полуплоскостей.
- Диагонали располагаются внутри многоугольника.
- Если концы отрезка располагаются в точках, которые принадлежат многоугольнику, весь отрезок принадлежит ему.
- Фигура может называться правильной, если у нее все отрезки и все углы равны. Примерами могут служить квадрат, равносторонний треугольник или правильный пятиугольник.
- Если n-угольник невыпуклый, все стороны и углы его равны, а вершины совпали с таковыми правильного n-угольника, он называется звездчатым. У таких фигур могут иметься самопересечения. Примерами могут служить пентаграмма или гексаграмма.
- Треугольник или четырехугольник называется вписанным в окружность, когда все его вершины располагаются внутри одной окружности. Если же стороны этой фигуры имеют точки соприкосновения с окружностью, это многоугольник описанным около некоторой окружности.
Любой выпуклый n-угольник можно поделить на треугольники. При этом количество треугольников бывает меньше количества сторон на 2.
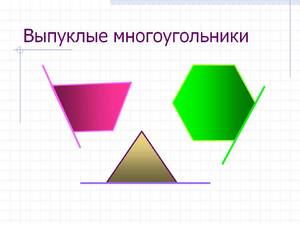
Виды фигур
Треугольник
Это многоугольник с тремя вершинами и тремя отрезками, соединяющими их. При этом точки соединения отрезков не лежат на одной прямой.
Точки соединения отрезков — это вершины треугольника. Сами отрезки называются сторонами треугольника. Общая сумма внутренних углов каждого треугольника равняется 180°.
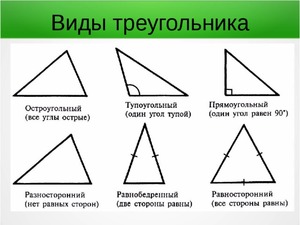
По соотношениям между сторонами все треугольники можно подразделять на несколько видов:
- Равносторонние — у которых длина всех отрезков одинаковая.
- Равнобедренные — треугольники, у которых равны два отрезка из трех.
- Разносторонние — если длина всех отрезков разная.
Кроме того, принято различать следующие треугольники:
- Остроугольные.
- Прямоугольные.
- Тупоугольные.
Четырехугольник
Четырехугольником называется плоская фигура, имеющая 4 вершины и 4 отрезка, которые их последовательно соединяют.
- Если все углы четырехугольника прямые — эта фигура называется прямоугольником.
- Прямоугольник, у которого все стороны имеют одинаковую величину, называется квадратом.
- Четырехугольник, все стороны которого равны, называется ромбом.
На одной прямой не может находиться сразу три вершины четырехугольника.
Видео
Дополнительную информацию о многоугольниках вы найдете в этом видео.
Четырехугольником ABCD называется фигура, которая состоит из четырех точек А, В, С, D по три, не лежащих на одной прямой, и четырех отрезков AB, BC, CD и AD, соединяющих эти точки.
На рисунках изображены четырехугольники.
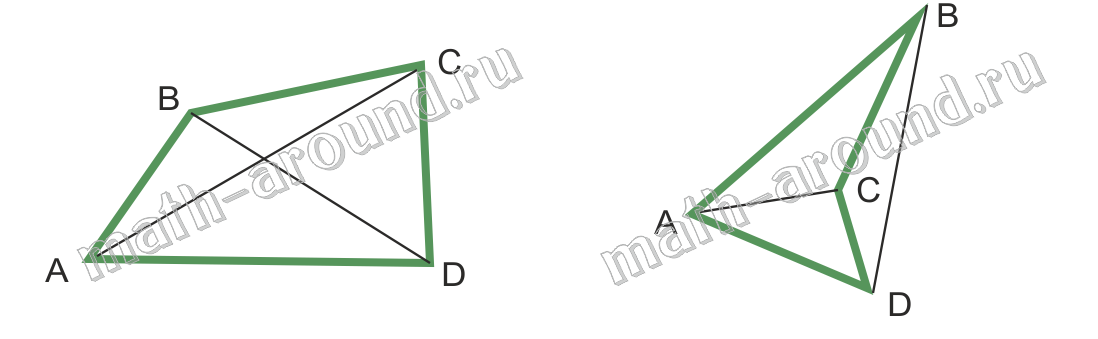
Точки А, В, С и D называются вершинами четырехугольника, а отрезки AB, BC, CD и AD — сторонами. Вершины А и С, В и D называются противолежащими вершинами. Стороны AB и CD, BC и AD называются противолежащими сторонами.
Четырехугольники бывают выпуклые (на рисунке — левый) и невыпуклые (на рисунке — правый).
Каждая диагональ выпуклого четырехугольника разделяет его на два треугольника (диагональ АС разделяет ABCD на два треугольника ABC и ACD; диагональ BD — на BCD и BAD). У невыпуклого четырехугольника только одна из диагоналей разделяет его на два треугольника (диагональ AC разделяет ABCD на два треугольника ABC и ACD; диагональ BD — не разделяет).
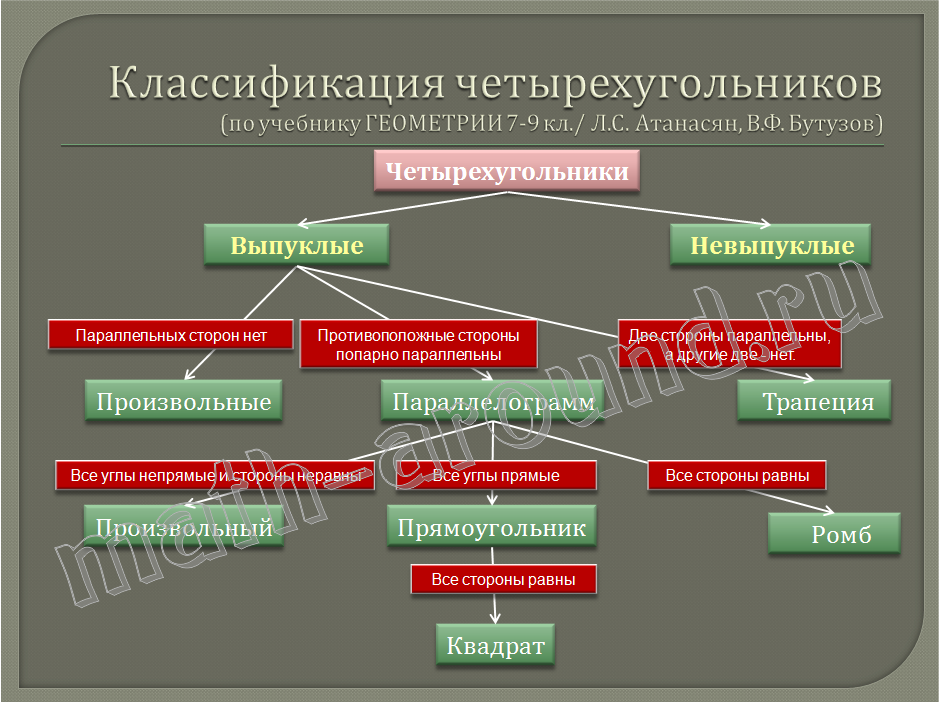
Рассмотрим основные виды четырехугольников, их свойства, формулы площади:
Параллелограмм
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
 | ABCD-параллелограмм: AB||DC, AD||BC |
Свойства:
|  |
| 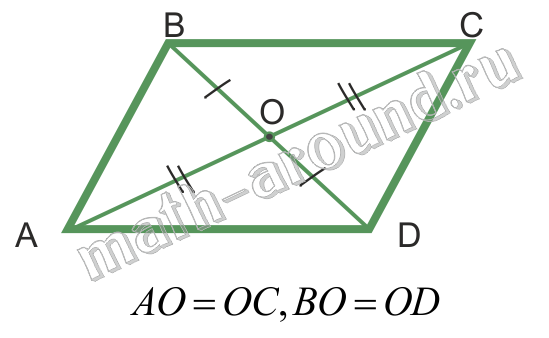 |
Признаки параллелограмма:
1. Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
2. Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Площадь параллелограмма:
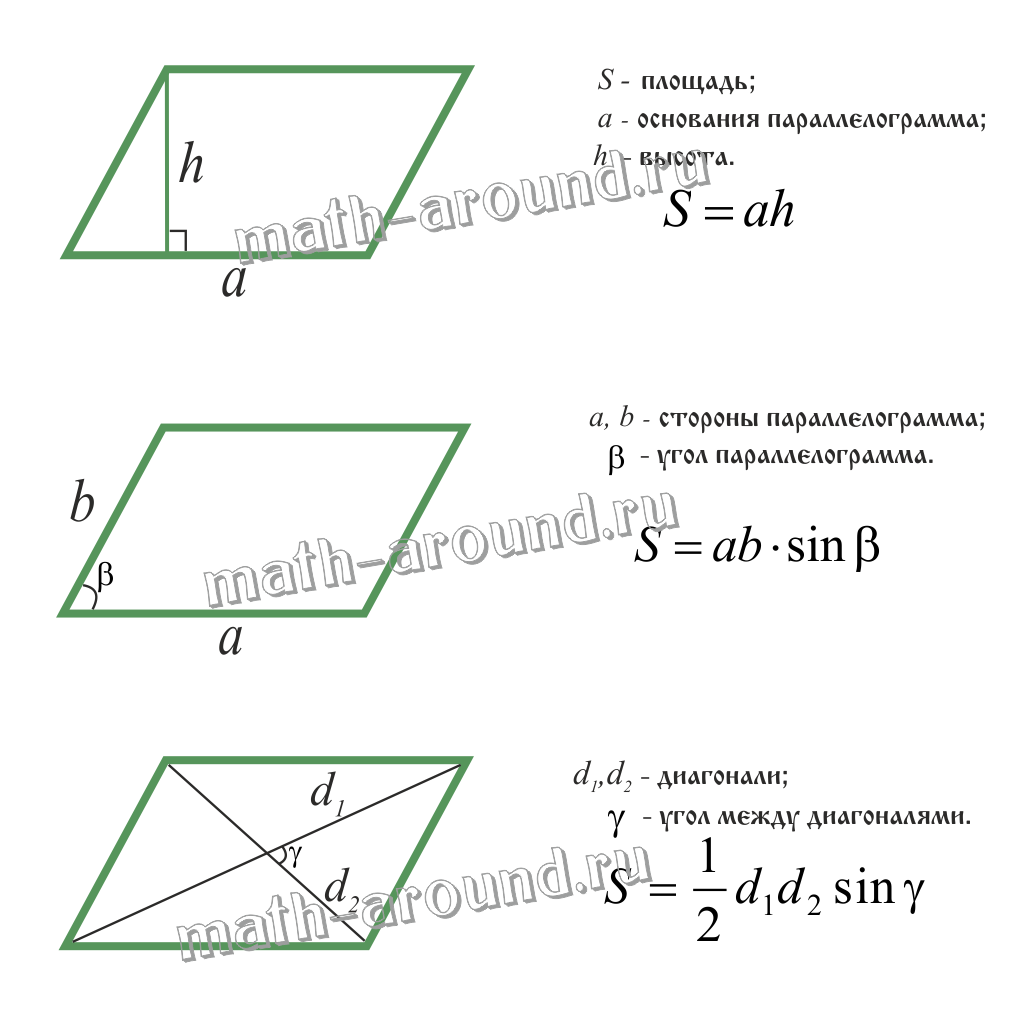
Трапеция
Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Основаниями называются параллельные стороны, а две другие стороны — боковыми сторонами.
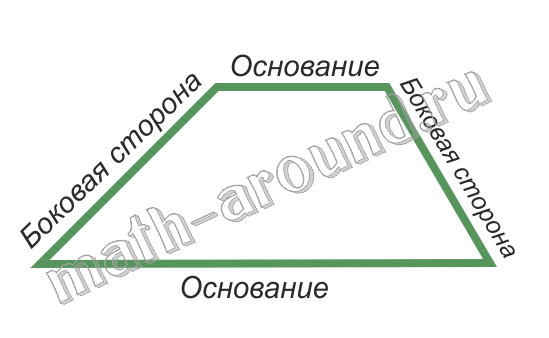
Средней линией трапеции называется отрезок, соединяющий середины ее боковых сторон.
ТЕОРЕМА.
Средняя линия трапеции параллельна основаниям и равна их полусумме.
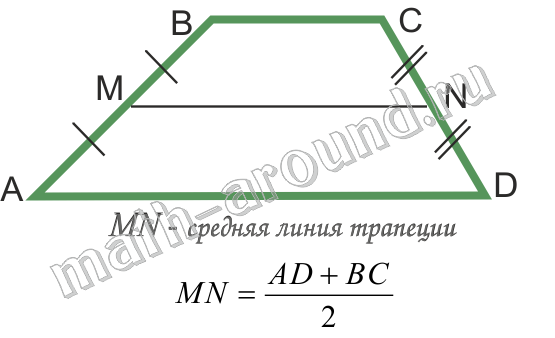
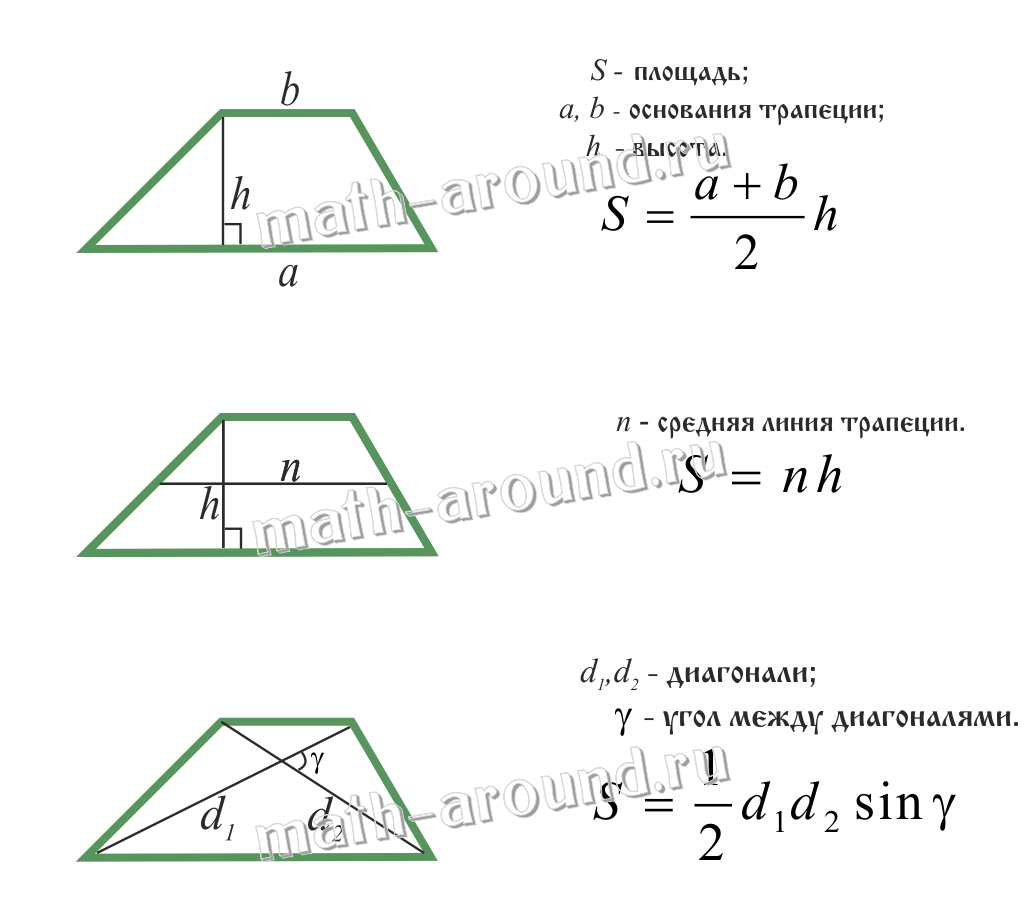
Площадь трапеции:
Ромб
Ромбом называется параллелограмм, у которого все стороны равны.
Свойства:
|  |
|  |
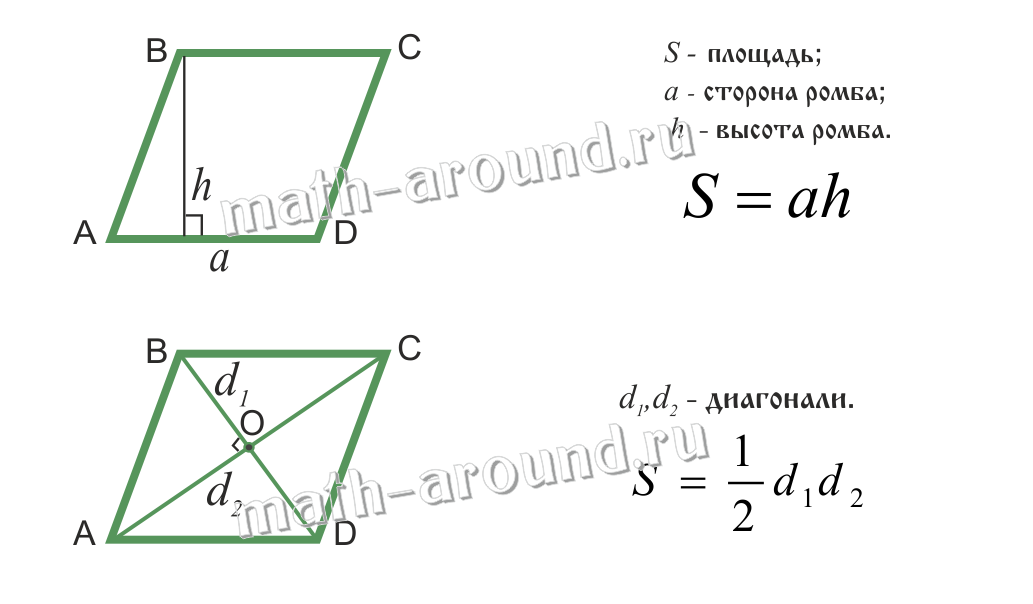
Площадь ромба:
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы равны.
Свойства:
|  |
|  |
Признак прямоугольника:
Если в параллелограмме диагонали равны, то этот параллелограмм – прямоугольник.
Площадь прямоугольника:

Квадрат
Квадратом называется прямоугольник, у которого все стороны равны.
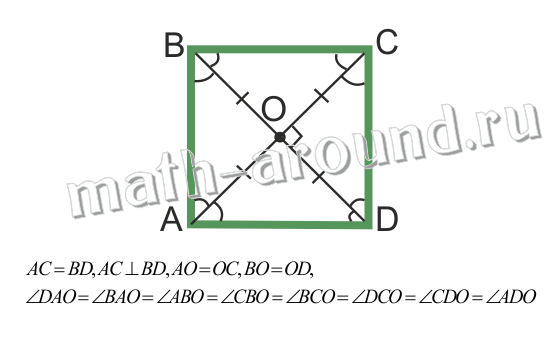
Свойства:
Квадрат обладает всеми свойствами прямоугольника и ромба (прямоугольник является параллелограммом, поэтому и квадрат является параллелограммом, у которого все стороны равны, т.е. ромбом).
|  |
|  |
Площадь квадрата:

Геометрия
7-9 классы
Отображение плоскости на себя
Слово «движение» вам знакомо. Но в геометрии оно имеет особый смысл. Какой именно, об этом вы узнаете из данной главы. А пока отметим, что с помощью движений удаётся находить красивые решения многих геометрических задач. Примеры таких решений вы найдёте в этой главе.
Представим себе, что каждой точке плоскости сопоставляется (ставится в соответствие) какая-то точка этой же плоскости, причём любая точка плоскости оказывается сопоставленной некоторой точке. Тогда говорят, что дано отображение плоскости на себя.
Фактически мы уже встречались с отображениями плоскости на себя — вспомним осевую симметрию (см. п. 48). Она даёт нам пример такого отображения. В самом деле, пусть а — ось симметрии (рис. 321). Возьмём произвольную точку М, не лежащую на прямой а, и построим симметричную ей точку М1 относительно прямой а. Для этого нужно провести перпендикуляр МР к прямой а и отложить на прямой МР отрезок РМ1, равный отрезку МР, так, как показано на рисунке 321. Точка М1 и будет искомой. Если же точка М лежит на прямой а, то симметричная ей точка М1 совпадает с точкой М. Мы видим, что с помощью осевой симметрии каждой точке М плоскости сопоставляется точка М, этой же плоскости. При этом любая точка М1 оказывается сопоставленной некоторой точке М. Это ясно из рисунка 321.

Рис. 321
Итак, осевая симметрия представляет собой отображение плоскости на себя.
Рассмотрим теперь центральную симметрию плоскости (см. п. 48). Пусть О — центр симметрии. Каждой точке М плоскости сопоставляется точка М1, симметричная точке М относительно точки О (рис. 322). Попытайтесь самостоятельно убедиться в том, что центральная симметрия плоскости также представляет собой отображение плоскости на себя.

Рис. 322
Понятие движения
Осевая симметрия обладает следующим важным свойством — это отображение плоскости на себя, которое сохраняет расстояния между точками.
Поясним, что это значит. Пусть М и N — какие-либо точки, а М1 и N1 — симметричные им точки относительно прямой а (рис. 323). Из точек N и N1 проведём перпендикуляры NP и N1P1 к прямой ММ1. Прямоугольные треугольники MNP и M1N1P1 равны по двум катетам: МР = М1Р1 и NP = N1P1 (объясните, почему эти катеты равны). Поэтому гипотенузы MN и M1N1 также равны.

Рис. 323
Следовательно, расстояние между точками М и N равно расстоянию между симметричными им точками М1 и N1. Другие случаи расположения точек М, N и М1, N1 рассмотрите самостоятельно и убедитесь в том, что и в этих случаях MN = M1N1 (рис. 324). Таким образом, осевая симметрия является отображением, которое сохраняет расстояния между точками. Любое отображение, обладающее этим свойством, называется движением (или перемещением).

Рис. 324
Итак, движение плоскости — это отображение плоскости на себя, сохраняющее расстояния.
Почему отображение, сохраняющее расстояния, называют движением (или перемещением), можно пояснить на примере осевой симметрии. Её можно представить как поворот плоскости в пространстве на 180° вокруг оси а. На рисунке 325 показано, каким образом происходит такой поворот.

Рис. 325
Отметим, что центральная симметрия плоскости также является движением (пользуясь рисунком 326, убедитесь в этом самостоятельно).

Рис. 326
Докажем следующую теорему:
Теорема
При движении отрезок отображается на отрезок.
Доказательство
Пусть при заданном движении плоскости концы М и N отрезка MN отображаются в точки М1 и N1 (рис. 327). Докажем, что весь отрезок MN отображается на отрезок M1N1. Пусть Р — произвольная точка отрезка MN, Р1 — точка, в которую отображается точка Р. Тогда МР + PN = MN. Так как при движении расстояния сохраняются, то
M1N1 = MN, М1Р1 = МР и N1P1 = NP. (1)

Рис. 327
Из равенств (1) получаем, что М1Р1 + P1N1 = M1N1, и, значит, точка Р1 лежит на отрезке M1N1 (если предположить, что это не так, то будет выполняться неравенство М1Р1 +P1N1 > M1N1). Итак, точки отрезка MN отображаются в точки отрезка M1N1.
Нужно ещё доказать, что в каждую точку Р1 отрезка M1N1 отображается какая-нибудь точка Р отрезка MN. Докажем это. Пусть Р1 — произвольная точка отрезка M1N1, и точка Р при заданном движении отображается в точку Р1. Из соотношений (1) и равенства M1N1 = М1Р1 + P1N1 следует, что МР + PN = MN, и, значит, точка Р лежит на отрезке MN. Теорема доказана.
Следствие
При движении треугольник отображается на равный ему треугольник.
В самом деле, в силу доказанной теоремы при движении каждая сторона треугольника отображается на равный ей отрезок, поэтому и треугольник отображается на треугольник с соответственно равными сторонами, т. е. на равный треугольник.
Пользуясь доказанной теоремой, нетрудно убедиться в том, что при движении прямая отображается на прямую, луч — на луч, а угол — на равный ему угол.
Наложения и движения
Напомним, что в нашем курсе геометрии равенство фигур определяется с помощью наложений. Мы говорим, что фигура Ф равна фигуре Фп если фигуру Ф можно совместить наложением с фигурой Ф1. Понятие наложения в нашем курсе относится к основным понятиям геометрии, поэтому определение наложения не даётся. Под наложением фигуры Ф на фигуру Ф1 мы понимаем некоторое отображение фигуры Ф на фигуру Ф1 Более того, мы считаем, что при этом не только точки фигуры Ф, но и любая точка плоскости отображается в определённую точку плоскости, т. е. наложение — это отображение плоскости на себя.
Однако не всякое отображение плоскости на себя мы называем наложением. Наложения — это такие отображения плоскости на себя, которые обладают свойствами, выраженными в аксиомах (см. приложение 1, аксиомы 7—13). Эти аксиомы позволяют доказать все те свойства наложений, которые мы себе представляем наглядно и которыми пользуемся при доказательстве теорем и решении задач. Докажем, например, что при наложении различные точки отображаются в различные точки.
В самом деле, предположим, что это не так, т. е. при некотором наложении какие-то две точки А и В отображаются в одну и ту же точку С. Тогда фигура Ф1, состоящая из точек А и В, равна фигуре Ф2, состоящей из одной точки С. Отсюда следует, что Ф2 = Ф1 (аксиома 12), т. е. при некотором наложении фигура Ф2 отображается в фигуру Ф1. Но это невозможно, так как наложение — это отображение, а при любом отображении точке С ставится в соответствие только одна точка плоскости.
Из доказанного утверждения следует, что при наложении отрезок отображается на равный ему отрезок. Действительно, пусть при наложении концы А и В отрезка АВ отображаются в точки А1 и В1. Тогда отрезок АВ отображается на отрезок А1В1 (аксиома 7), и, следовательно, отрезок АВ равен отрезку А1В1. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, сохраняющим расстояния, т. е. любое наложение является движением плоскости.
Докажем, что верно и обратное утверждение.
Теорема
Любое движение является наложением.
Доказательство
Рассмотрим произвольное движение (обозначим его буквой g) и докажем, что оно является наложением. Возьмём какой-нибудь треугольник АВС. При движении g он отображается на равный ему треугольник А1В1С1. По определению равных треугольников существует наложение ƒ, при котором точки А, В и С отображаются соответственно в точки А1, В1 и С1.
Докажем, что движение g совпадает с наложением ƒ. Предположим, что это не так. Тогда на плоскости найдётся хотя бы одна такая точка М, которая при движении g отображается в точку М„ а при наложении ƒ — в другую точку М2. Так как при отображениях ƒ u g сохраняются расстояния, то AM = А1М1, AM = А1М2, поэтому A1M1 = А1М2, т. е. точка А1 равноудалена от точек М1 и М2 (рис. 328). Аналогично доказывается, что точки В1 и С1 равноудалены от точек М1 и М2. Отсюда следует, что точки А1, В1 и С1 лежат на серединном перпендикуляре к отрезку М1М2. Но это невозможно, так как вершины треугольника А1В1С1 не лежат на одной прямой. Таким образом, отображения ƒ u g совпадают, т. е. движение g является наложением. Теорема доказана.

Рис. 328
Следствие
При движении любая фигура отображается на равную ей фигуру.
Задачи
1148. Докажите, что при осевой симметрии плоскости:
а) прямая, параллельная оси симметрии, отображается на прямую, параллельную оси симметрии;
б) прямая, перпендикулярная к оси симметрии, отображается на себя.
1149. Докажите, что при центральной симметрии плоскости:
а) прямая, не проходящая через центр симметрии, отображается на параллельную ей прямую;
б) прямая, проходящая через центр симметрии, отображается на себя.
1150. Докажите, что при движении угол отображается на равный ему угол.
Решение
Пусть при данном движении угол АОВ отображается на угол A1O1B1, причём точки А, О, В отображаются соответственно в точки A1, О1, В1. Так как при движении сохраняются расстояния, то ОА = О1А1, ОВ = О1В1. Если угол АОВ неразвёрнутый, то треугольники АОВ и А1О1В1 равны по трём сторонам, и, следовательно, ∠AOB = ∠A1O1B1. Если угол АОВ развёрнутый, то и угол А1О1В1 развёрнутый (докажите это), поэтому эти углы равны.
1151. Докажите, что при движении параллельные прямые отображаются на параллельные прямые.
1152. Докажите, что при движении: а) параллелограмм отображается на параллелограмм; б) трапеция отображается на трапецию; в) ромб отображается на ромб; г) прямоугольник отображается на прямоугольник, а квадрат — на квадрат.
1153. Докажите, что при движении окружность отображается на окружность того же радиуса.
1154. Докажите, что отображение плоскости, при котором каждая точка отображается на себя, является наложением.
1155. АВС и А1В1С1 — произвольные треугольники. Докажите, что существует не более одного движения, при котором точки А, В и С отображаются в точки А1, В1, С1.
1156. В треугольниках АВС и А1В1С1 АВ = А1В1, АС = А1С1, ВС = В1С1. Докажите, что существует движение, при котором точки А, В и С отображаются в точки А1, В1 и С1, и притом только одно.
Решение
По условию задачи треугольники АВС и А1В1С1 равны по трём сторонам. Следовательно, существует наложение, т. е. движение, при котором точки А, В и С отображаются соответственно в точки А1, В1 и С1. Это движение является единственным движением, при котором точки А, В и С отображаются соответственно в точки А1, В1 и C1 (задача 1155).
1157. Докажите, что два параллелограмма равны, если смежные стороны и угол между ними одного параллелограмма соответственно равны смежным сторонам и углу между ними другого параллелограмма.
1158. Даны две прямые а и b. Постройте прямую, на которую отображается прямая b при осевой симметрии с осью а.
1159. Даны прямая а и четырёхугольник ABCD. Постройте фигуру F, на которую отображается данный четырёхугольник при осевой симметрии с осью а. Что представляет собой фигура F?
1160 Даны точка О и прямая b. Постройте прямую, на которую отображается прямая b при центральной симметрии с центром О.
1161 Даны точка О и треугольник АВС. Постройте фигуру F, на которую отображается треугольник АВС при центральной симметрии с центром О. Что представляет собой фигура F?
Ответы к задачам
1151. Указание. Доказать методом от противного.
1154. Указание. Воспользоваться теоремой п. 119.
1155. Указание. Доказательство провести методом от противного (см. доказательство теоремы п. 119).
1157. Указание. Воспользоваться задачами 1156 и 1051.
1158. Указание. Сначала построить образы каких-нибудь двух точек прямой b.
1159. F — четырёхугольник.
1160. Указание. Задача решается аналогично задаче 1158.
1161. F — треугольник.
