Функции у корень из х ее свойства и график какой график
Повторение понятия квадратного корня и графика функции y = √x
Данный урок мы посвятим решению типовых задач на построение графика функции . Вспомним определение квадратного корня.
Определение. Квадратным корнем из неотрицательного числа называется такое неотрицательное число , квадрат которого равен .
.
Изобразим график – это правая ветвь параболы (рис. 1).
Рис. 1.
На графике наглядно виден смысл вычисления квадратного корня. Например, если рассмотреть ординату 16, то ей будет соответствовать абсцисса 4, т. к. . Аналогично, ординате 9 на графике соответствует точка с абсциссой 3, поскольку , ординате 11 соответствует абсцисса , т. к. (квадратный корень из 11 не извлекается в целых числах).
Теперь вспомним график функции (рис. 2).
Рис. 2.
На графике для наглядности изображены несколько точек, ординаты которых вычисляются с помощью извлечения квадратного корня: , , .
Примеры на преобразование графиков с корнями
Пример 1. Постройте и прочтите график функции: а) , б) .
Решение. а) Построение начинается с простейшего вида функции, т. е. в данном случае с графика (пунктиром). Затем для построения искомого графика график функции необходимо сдвинуть влево на 1 (рис. 3). При этом все точки графика сдвинутся на 1 влево, например, точка с координатами (1;1) перейдет в точку с координатами (0;1). В результате получаем искомый график (красная кривая). Проверить такой способ легко при подстановке нескольких значений аргумента.
Рис. 3.
Прочтем график: если аргумент меняется от до , функция возрастает от 0 до . Область определения (ОДЗ) при этом требует, чтобы подкоренное выражение было неотрицательным, т. е. .
б) Для построения графика функции поступим аналогичным образом. Сначала строим график (пунктиром). Затем для построения искомого графика график функции необходимо сдвинуть вправо на 1 (рис. 4). При этом все точки графика сдвинутся на 1 вправо, например, точка с координатами (1;1) прейдет в точку с координатами (2;1). В результате получаем искомый график (красная кривая).
Рис. 4.
Прочтем график: если аргумент меняется от до , функция возрастает от 0 до . Область определения (ОДЗ) аналогична предыдущему случаю: .
Замечание. На указанных примерах несложно сформулировать правило построения функций вида:
.
Пример 2. Постройте и прочтите график функции: а) , б) .
Решение. а) Этот пример также демонстрирует преобразование графиков функций, но только уже другого типа. Начинаем построение с простейшей функции (пунктиром). Затем график построенной функции смещаем на 2 вверх и получаем на рисунке 5 искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;3).
Рис. 5.
Прочтем график: если аргумент меняется от 0 до , функция возрастает от 2 до . Область определения (ОДЗ): .
б) Также начинаем построение с простейшей функции (пунктиром). Затем график построенной функции (рис. 6) смещаем на 1 вниз и получаем искомый график (красная кривая). Точка с координатами (1;1) при этом, например, переходит в точку (1;0).
Рис. 6.
Прочтем график: если аргумент меняется от 0 до , функция возрастает от до . Область определения (ОДЗ): .
Замечание. С помощью указанных примеров сформулируем правило построения функций вида:
.
Пример 3. Постройте и прочтите график функции .
Решение. Метод построения указанной функции представляет собой комбинацию двух методов, которые мы видели в предыдущих примерах. Сначала строим основную функцию (пунктиром), затем смещаем ее на 1 вправо и на 2 вверх (рис. 7). При этом, например, точка с координатами (1;1) сначала перейдет в точку (2;1), а затем в точку (2;3). Искомая кривая изображена красным цветом.
Рис. 7.
Прочтем график: если аргумент меняется от до , функция возрастает от 2 до . Область определения (ОДЗ) – подкоренное выражение неотрицательно: .
Замечание. Как видно на указанном примере, преобразования графиков функций, которые мы рассмотрели, можно применять последовательно в комплексе.
Пример 4. Постройте и прочтите график функции .
Решение. Для построения данной составной функции изображаем ее части в приведенных диапазонах построения (рис. 8). Для этого сначала изображаем пунктиром всю функцию , затем всю функцию , а затем наводим (красная кривая) только те их области, которые заданы условием задачи. Сливаются два участка кривой в точке с координатами (1;1).
Рис. 8.
Прочтем график: если аргумент меняется от до 1, функция возрастает от 0 до , если аргумент меняется от 1 до , функция убывает от 1 до 0. Область определения (ОДЗ) – подкоренное выражение неотрицательно: .
Пример на решение системы уравнений с квадратным корнем
Пример 5. Графически решить систему уравнений .
Решение. Для решения системы графическим способом необходимо построить графики функций (рис. 9), представляющих собой уравнения системы, и определить координаты их точек пересечения.
Рис. 9.
На графике изображен полезный факт, демонстрирующий, что графики квадратичной функции и квадратного корня симметричны относительно графика функции . По графику видно, что имеем две точки пересечения, т. е. система имеет два решения. Для определения точных значений этих решений подставим стандартные значения аргумента в обе исследуемые функции: 0 и 1. При этом получим: и , т. е. координаты точек пересечения графиков и решения системы: и .
Ответ. (0;0), (1;1).
Пример на решения уравнения с параметром
Пример 6. (С параметром). При каких значениях параметра имеет решение уравнение ?
Решение. Для исследования значений параметра воспользуемся графическим методом и построим график функции . Мы его уже строили на сегодняшнем уроке, поэтому воспользуемся готовым рисунком 10.
Рис. 10.
Прочтем график: если аргумент меняется от до , функция возрастает от 2 до . Из этого следует, что функция принимает значения только , причем при аргументе она принимает свое минимальное значение . Из полученного диапазона изменения можно сделать однозначный вывод, что параметр , который в уравнении приравнивается к рассмотренной функции, может принимать такие же значения . Например, при имеем, что , т. е. у уравнения есть корень и т. д.
Ответ..
На следующем уроке мы рассмотрим свойства квадратных корней.
Список литературы
1. Башмаков М.И. Алгебра 8 класс. – М.: Просвещение, 2004.
2. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
3. Никольский С.М., Потапов М.А., Решетников Н.Н., Шевкин А.В. Алгебра 8 класс. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2006.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Математика = это легко! 😉 (Источник).
2. Фестиваль педагогических идей «Открытый урок» (Источник).
3. Квадратный корень из х (Источник).
Домашнее задание
1. №313, 316, 317. Дорофеев Г.В., Суворова С.Б., Бунимович Е.А. и др. Алгебра 8. – 5-е изд. – М.: Просвещение, 2010.
2. Решите графически уравнение .
3. Постройте график функции .
4. Решите графически уравнение:
Ãðàôèê ôóíêöèè êâàäðàòíîãî êîðíÿ: 
:
Êâàäðàòíûé êîðåíü êàê ýëåìåíòàðíàÿ ôóíêöèÿ.
Êâàäðàòíûé êîðåíü – ýòî ýëåìåíòàðíàÿ ôóíêöèÿ è ÷àñòíûé ñëó÷àé ñòåïåííîé ôóíêöèè 
ïðè 
. Àðèôìåòè÷åñêèé êâàäðàòíûé êîðåíü ÿâëÿåòñÿ ãëàäêèì ïðè 
, à íóëå îí íåïðåðûâåí ñïðàâà, íî íå äèôôåðåíöèðóåòñÿ.
Êàê ôóíêöèÿ êîìïëåêñíûé ïåðåìåííûé êîðåíü — äâóçíà÷íàÿ ôóíêöèÿ, ó êîòîðîé ëèñòû ñõîäÿòñÿ â íóëå.
Ïîñòðîåíèå ãðàôèêà ôóíêöèè êâàäðàòíîãî êîðíÿ.
- Çàïîëíÿåì òàáëèöó äàííûõ:
õ | 1 | 4 | 9 |
ó | 1 | 2 | 3 |
2. Íàíîñèì òî÷êè, êîòîðûå ìû ïîëó÷èëè íà êîîðäèíàòíóþ ïëîñêîñòü.
3. Ñîåäèíÿåì ýòè òî÷êè è ïîëó÷àåì ãðàôèê ôóíêöèè êâàäðàòíîãî êîðíÿ:
Ïðåîáðàçîâàíèÿ ãðàôèêà ôóíêöèè êâàäðàòíîãî êîðíÿ.
Îïðåäåëèì, êàêèå ïðåîáðàçîâàíèÿ ôóíêöèè íåîáõîäèìî ñäåëàòü äëÿ òîãî, ÷òîáû ïîñòðîèòü ãðàôèêè ôóíêöèé. Îïðåäåëèì âèäû ïðåîáðàçîâàíèé.
Ïðèìåð | Âèä ïðåîáðàçîâàíèÿ | Ïðåîáðàçîâàíèå |
| âíåøíåå | Ïåðåíîñ ôóíêöèè ïî îñè OY íà 4 åä. ââåðõ. |
| âíóòðåííåå | Ïåðåíîñ ôóíêöèè ïî îñè OX íà 1 åä. âïðàâî. |
| âíóòðåííåå | Ãðàôèê ïðèáëèæàåòñÿ ê îñè OY â 3 ðàçà è ñæèìàåòñÿ ïî îñè OÕ. |
| âíåøíåå | Ãðàôèê îòäàëÿåòñÿ îò îñè OX â 2 ðàçà è ðàñòÿãèâàåòñÿ ïî îñè OY. |
| âíóòðåííåå | Ãðàôèê îòäàëÿåòñÿ îò îñè OY â 2 ðàçà è ðàñòÿãèâàåòñÿ ïî îñè OÕ. |
| âíóòðåííåå | Ñèììåòðè÷íîå îòîáðàæåíèå ãðàôèêà îòíîñèòåëüíî îñè ÎX. |
| êîìáèíèðîâàííîå | Ïðåäûäóùèé ãðàôèê îòäàëÿåòñÿ îò îñè OX â 3 ðàçà è ðàñòÿãèâàåòñÿ ïî îñè OY. |
| êîìáèíèðîâàííîå | Ñèììåòðè÷íîå îòðàæåíèå ãðàôèêà îòíîñèòåëüíî îñè OY, ïðè ýòîì âåðõíÿÿ ÷àñòü ãðàôèêà I ÷åòâåðòè îñòà¸òñÿ áåç èçìåíåíèé, à íàõîäÿùàÿñÿ â II ÷åòâåðòè ãðàôèê èñ÷åçàåò, ñèììåòðè÷íî îòîáðàæàÿñü îòíîñèòåëüíî îñè OX. |
Çà÷àñòóþ ïðåîáðàçîâàíèÿ ôóíêöèé îêàçûâàþòñÿ êîìáèíèðîâàííûìè.
Íàïðèìåð, íóæíî ïîñòðîèòü ãðàôèê ôóíêöèè 
. Ýòî ãðàôèê êâàäðàòíîãî êîðíÿ 
, êîòîðûé íóæíî ïåðåíåñòè íà îäíó åäèíèöó âíèç ïî îñè OY è íà åäèíèöó âïðàâî ïî îñè ÎÕ è îäíîâðåìåííî ðàñòÿíóâ â 3 ðàçà åãî ïî îñè OY.
Áûâàåò íåïîñðåäñòâåííî ïåðåä ïîñòðîåíèåì ãðàôèêà ôóíêöèè, íóæíû ïðåäâàðèòåëüíûå òîæäåñòâåííûå ïðåîáðàçîâàíèÿ ëèáî óïðîùåíèÿ ôóíêöèé.
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó àëãåáðû äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Àëãåáðà 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Êâàäðàòíûé êîðåíü. | |
| Ñâîéñòâà êâàäðàòíûõ êîðíåé, äðîáíûå ñòåïåíè, êîðåíü n-íîé ñòåïåíè, ïðèìåðû âû÷èñëåíèÿ âûðàæåíèé ñ êîðíÿìè è äðóãîå. | |
| Êâàäðàòíûé êîðåíü. | |
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = √х , ее свойства и график
Функция у = √х , ее свойства и график
Для построения графика функции 
дадим, как обычно, независимой переменной х несколько конкретных значений (неотрицательных, поскольку при х < 0 выражение 
не имеет смысла) и вычислим соответствующие значения зависимой переменной у. Разумеется, мы будем давать х такие значения, для которых известно точное значение квадратного корня. Итак:
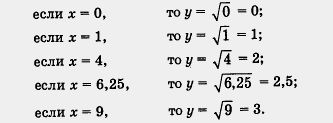
Итак, мы составили таблицу значений функции:
| x | 0 | 1 | 4 | 6,25 | 9 |
| y | 0 | 1 | 2 | 2,5 | 3 |
Построим найденные точки (0; 0), (1;1), (4; 2), (6,25; 2,5), (0;3) на координатной плоскости (рис. 78). Они располагаются некоторой линии, начертим ее (рис. 79). Получили график функции . Обратите внимание: график касается оси у в точке (0; 0). Заметим, что, имея шаблон параболы у = х2, можно без труда с его помощью построить график функции , ведь это — ветвь той же параболы, только ориентированная не вверх, а вправо.
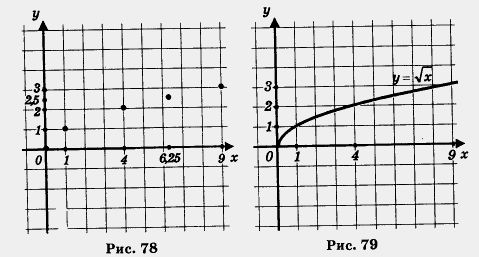
Свойства функции
Описывая свойства этой функции, мы, как обычно, будем опираться на ее геометрическую модель — ветвь параболы (рис. 79).
1. Область определения функции — луч [0, +оо).
2. у = 0 при х = 0; у > 0 при х > 0.
3. Функция возрастает на луче [0, + оо).
4. Функция ограничена снизу, но не ограничена сверху.
5. унаим. = 0 (достигается при х = 0), унаи6 не существует.
6. Функция непрерывна на луче [0, +оо).
Комментариев требует лишь свойство 4. Почему мы считаем, что функция не ограничена сверху? Возьмем, например, число 10. Найдется ли такое значение х, для которого будет выполнено неравенство > 10? Конечно, достаточно взять х = 121, ведь 
= 11, а 11 > 10. Возьмем число 40. Найдется ли такое значение х, для которого будет выполняться неравенство > 40? Конечно, достаточно взять х = 2500, ведь 
= 50, а 50 > 40. И вообще, какое бы положительное число т ни взять, всегда найдется такое х, что будет выполняться неравенство > m (достаточно взять х = (m + 1)2; подумайте, почему это так).
А теперь обратим внимание на одно любопытное обстоятельство. Рассмотрим две функции: у = (ее график изображен на рис. 79) и у = х2, где х> 0 (ее график изображен на рис. 80). Мы только что перечислили шесть свойств для первой функции, но абсолютно теми же свойствами обладает и вторая функция. Словесные «портреты» двух различных функций одинаковы. Математики не смогли вынести такой несправедливости, когда разные функции, имеющие разные графики, словесно описываются одинаково. Они обнаружили принципиальные различия в характере графиков, заметив, что график функции обращен выпуклостью вверх, тогда как
график функции у = х2, где х > 0, обращен выпуклостью вниз.
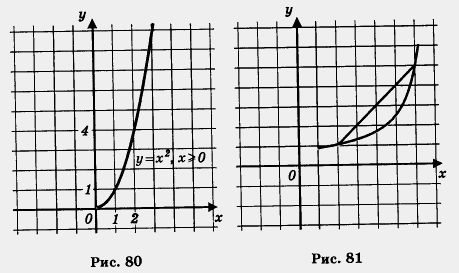
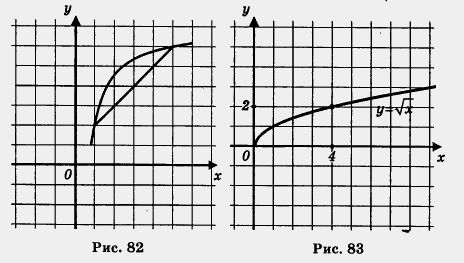
Обычно говорят, что функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка (рис. 81); функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка (рис. 82).
Свойство выпуклости будем в дальнейшем включать в процедуру чтения графика.
Функция у = f (х)у где f (х) = , принимает любые неотрицательные значения. В самом деле, какое бы конкретное значение у > 0 ни задать, всегда найдется такое х, что выполняется равенство f (х) = у, т.е. = у; для этого достаточно положить х = у2. Множество всех значений функции называют обычно областью значений функции. Для функции у = областью значения значений является луч [0, + оо). Это, кстати, хорошо читается по графику функции (рис. 79). Если спроецировать график на ось у, как раз и получится луч [0, + оо ).
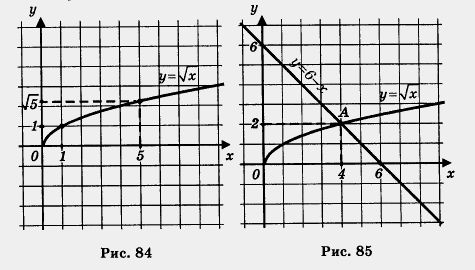
Пример 1. Найти наименьшее и наибольшее значения функции у = на отрезке:
а) [0, 4]; б) [1, 5].
Решение, а) Построим график функции у = и выделим его часть на отрезке [0, 4] (рис. 83). Замечаем, что Унаим. = 0 (достигается при х = 0), а унаи6 = 2 (достигается при х = 4).
б) Построим график функции у = и выделим его часть на отрезке [1, 5] (рис. 84). Замечаем, что унаим = 1 (достигается при х = 1), а унаиб = 
(достигается при х = 5).
О т в е т: а) унаим. = 0; унаиб = 2; б) унаим. = 1; ушиб =
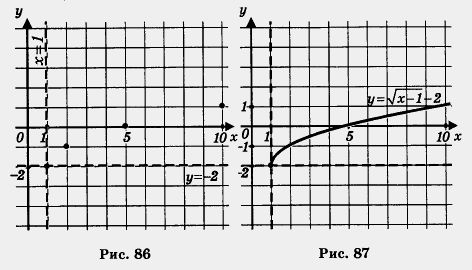
Пример 2. Решить уравнение = 6 — х.
Решение.
1) Рассмотрим две функции у = 6 — x и y =
2) Построим график функции у = (рис. 85).
3) Построим график линейной функции у = 6 — х.
Это — прямая, которую можно построить по двум точкам (0; 6) и (6; 0). Прямая изображена на том же чертеже (рис. 85).
4) По чертежу устанавливаем, что графики пересекаются в одной точке А (4; 2). Так ли это на самом деле? Проверим: пара (4; 2) удовлетворяет и уравнению у = и уравнению у = 6 — х.
Это значит, что точка (4; 2) на самом деле служит точкой пересечения построенных графиков. Заданное уравнение имеет один корень 4 — это абсцисса точки А.
Ответ: 4.
Пример 3. Построить график функции 
Решение. 1) Перейдем к вспомогательной системе координат с началом в точке (1; -2) (пунктирные прямые х = 1 и у = — 2 на рис. 86).
2) Привяжем функцию у = к новой системе координат.
Для этого выберем контрольные точки для функции у = . , например (0; 0), (1; 1), (4; 2), (9; 3), но строить их будем не в старой, а в новой системе координат (эти точки отмечены на рис. 86). Построим ветвь параболы, проходящую через выбранные точки, — это и есть требуемый график (рис. 87).
Пример 4. Построить и прочитать график функции y = —
Решение. Выше, в § 8, мы заметили, что график функции у = — f (х) получается из графика функции у = f (x) с помощью преобразования симметрии относительно оси х.
Воспользовавшись этим, построим график функции у = и отобразим его симметрично относительно оси х (рис. 88). Это и будет график функции у = — .
Перечислим свойства функции у = — (по графику):
1. Область определения функции — луч [0, + оо).
2. у = 0 при х = 0; у < 0 при х > 0.
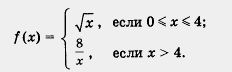
3. Функция убывает на луче [0, + оо).
4. Функция ограничена сверху и не ограничена снизу.
5 Унаиб. = 0 (достигается при х = 0), унаим не существует.
6. Функция непрерывна на луче [0, + од).
7. Область значений функции — луч (- оо, 0].
8. Функция выпукла вниз.
Пример 5. Построить и прочитать график функции y =f(x), где
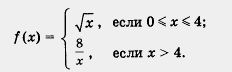
Решение. Сначала построим график функции у = и выделим его часть на отрезке [0, 4] (рис. 89). Затем построим гиперболу 
и выделим ее часть на открытом луче (4, + оо) (рис. 90). Наконец, оба «кусочка» изобразим в одной системе координат — это и есть график функции у = f(x) (рис. 91).
Перечислим свойства функции у — f(x), т.е. прочитаем график.
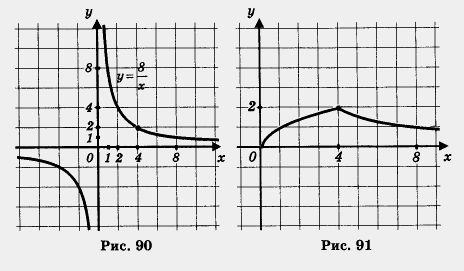
1. Область определения функции — луч [0, + °о).
2. у = 0 при x = 0; у > 0 при х > 0.
3. Функция возрастает на отрезке [0, 4] и убывает на луче [4, + оо).
4. Функция ограничена и снизу и сверху.
5 Унаим. = 0 (достигается при х = 0); унаи6 = 2 (достигается при х = 4).
6. Функция непрерывна в заданной области определения.
7. Область значений функции — отрезок [0, 2].
8. Функция выпукла вверх на отрезке [0, 4] и выпукла вниз на луче [4, + оо).
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Рефераты, домашняя работа по математике скачать, учебники скатать бесплатно, онлайн уроки, вопросы и ответы
Содержание урока
конспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии
Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников
Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты
Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие
Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми
Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 