Что такое ромб квадрат какие их свойства
У этого термина существуют и другие значения, см. Ромб (значения).
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1].
Этимология[править | править код]
Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.
Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.
Свойства[править | править код]
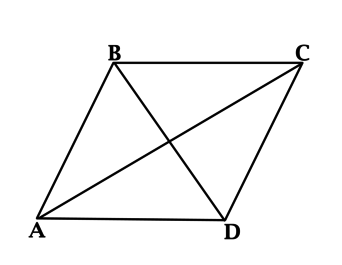
- Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
- Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
- Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
- Середины четырех сторон ромба являются вершинами прямоугольника.
- Диагонали ромба являются перпендикулярными осями его симметрии.
- В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Признаки[править | править код]
Параллелограмм является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:
- Две его смежные стороны равны (отсюда следует, что все стороны равны, ).
- Его диагонали пересекаются под прямым углом (AC ⊥ BD).
- Одна из диагоналей делит содержащие её углы пополам.
Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].
Квадрат, как частный случай ромба[править | править код]
Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.
Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4].
Уравнение ромба[править | править код]
Уравнение ромба с центром в точке и диагоналями, параллельными осям координат, может быть записано в виде:
где — половины длин диагоналей ромба по осям соответственно.
Длина стороны ромба равна Площадь ромба равна Левый угол ромба рассчитывается по формуле:
Второй угол дополняет его до 180°.
В случае a = b уравнение отображает повёрнутый на 45° квадрат:
где сторона квадрата равна а его диагональ равна Соответственно площадь квадрата равна
Из уравнения видно, что ромб можно рассматривать как суперэллипс степени 1.
Площадь ромба[править | править код]
- Площадь ромба равна половине произведения его диагоналей.
- Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
- Кроме того, площадь ромба может быть вычислена по формуле:
,
где — угол между двумя смежными сторонами ромба.
- Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол :
Радиус вписанной окружности[править | править код]
Радиус вписанной окружности r может быть выражен через диагонали p и q в виде:[5]
В геральдике[править | править код]
Ромб является простой геральдической фигурой.
Червлёный ромб в серебряном поле
В червлёном поле 3 сквозных ромба: 2 и 1
Просверленный червлёный ромб в серебряном поле
В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов
Симметрия[править | править код]
Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.
Ромбический орнамент
Ромбические звёзды
Более сложный орнамент
См. другие примеры на Викискладе.
См. также[править | править код]
- Дельтоид
- Звезда (геометрия)
- Ромбододекаэдр
Примечания[править | править код]
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Автор:
02 апреля 2019 08:28
Мы все учили в школе геометрию, но с годами многое подзабыли. Чтобы не попасть впросак, когда ваш ребенок спросит, чем ромб отличается от квадрата, почитайте эту статью и вспомните, казалось бы, давно забытое.

Источник:
Очень часто четкое определение какого-либо предмета дает о нем практически полную информацию. Вот, например, ромб и квадрат – едва ли не самые распространенные геометрические фигуры. Глядя на них, мы понимаем, что они отличаются, но вот чем и как это объяснить простыми словами? Давайте разбираться.
Что представляет собой ромб
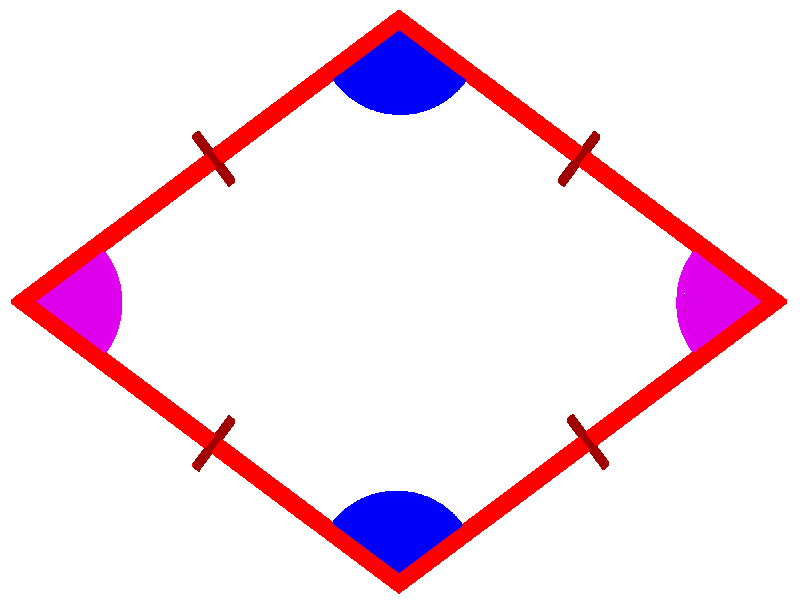
Источник:
Геометрия дает такое определение ромба: «Ромбом называется параллелограмм…». Стоп, сначала придется вспомнить, что такое параллелограмм. Это многоугольник с четырьмя углами, у которого противоположные стороны параллельны. А какими же свойствами обладает ромб как разновидность параллелограмма? Вот они:
1. Если соединить противоположные углы ромба диагоналями, то углы их пересечения составят 90º, то есть они взаимно перпендикулярны.
2. Эти диагонали (вообще-то в строгой науке геометрии принято говорить «отрезки диагоналей ромба») лежат на биссектрисах, делящих его углы пополам (помните школьный стишок: «Биссектриса – это такая крыса, которая бегает по углам и делит угол пополам»? Ребенку тоже будет полезно).
Что представляет собой квадрат
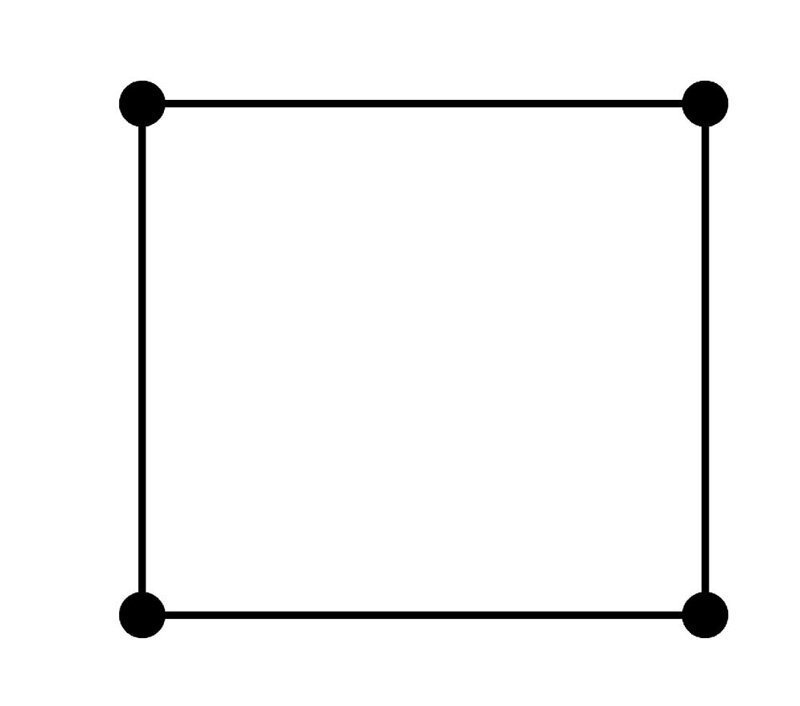
Источник:
С квадратом все намного проще, его определение звучит так: квадрат — это прямоугольник, у которого все стороны равны. Теперь нужно определить, что такое прямоугольник. Это тоже параллелограмм, как и ромб, но с прямыми углами, то есть равными 90º.
Основные свойства квадрата следующие:
1. Если провести биссектрисы всех углов квадрата (напомним, что углы прямые), то отрезки диагоналей квадрата будут лежать на этих биссектрисах.
2. Если провести диагонали между противоположными углами квадрата, то в центре симметрии квадрата, где эти диагонали пересекутся, они поделятся пополам.
3. Все отрезки диагоналей квадрата будут равны между собой.
Так в чем же отличие?

Источник:
Проще всего это понять и продемонстрировать ребенку с помощью спичек или зубочисток. Возьмите 4 спички и сделайте из них ромб. Обратите внимание на то, что у ромба разные углы: 2 острых и 2 тупых. А теперь превратите ромб в квадрат – просто сдвиньте спички таким образом, чтобы все углы стали прямыми, то есть по 90º.
Таким образом, получается, что квадрат – это как бы частный случай ромба (хотя настоящему специалисту это определение может показаться не совсем научным).
Еще одно отличие заключается в том, что у квадрата диагонали равны друг другу, а у ромба одна длиннее, а другая короче.
Вывод: каждый квадрат – это ромб с прямыми углами, но не каждый ромб – это квадрат.
Источник:
Ссылки по теме:

Понравился пост? Поддержи Фишки, нажми:
Конспект урока. 8 класс (учебник Л.С.Атанасян)
Тема урока: Ромб, квадрат и их свойства
Тип урока:
1) по основной дидактической цели: урок открытия нового знания.
2) по основному способу проведения: сочетание различных форм занятий.
3)по форме проведения: комбинированный урок.
Цели урока: Создание условий для усвоения учащимися понятий ромба, квадрата, их свойств.
Задачи урока:
1) образовательные:
Формировать:
-понятия ромба и квадрата как частных видов параллелограмма;
-умение формулировать свойства ромба, квадрата;
-умение построения ромба и квадрата;
-умения применять свойства ромба и квадрата при решении задач.
2) Развивающие:
-Развивать мышление, память, математический язык, осуществлять самостоятельную деятельность на уроке.
-Развивать умения систематизировать полученные знания.
-Развивать умение высказывать свое мнение, делать выводы;
Формы обучения: индивидуальная, фронтальная, групповая.
Оборудование: доска, мультимедиа, карточки с заданиями, раздаточный материал с заданиями.
План урока:
I . Организационный момент
II. Актуализация опорных знаний
III. Формирование новых знаний
IV. Применение знаний, формирование умений и навыков.
V. Теоретическая самостоятельная работа.
VI. Постановка домашнего задания
VII. Подведение итогов урока
VIII. Рефлексия
I. Организационный момент
Приветствие. Проверка готовности к уроку.
2. Мотивация учебной деятельности учащихся.
II. Актуализация опорных знаний.
Мы с вами изучили свойства и признаки некоторых четырехугольников. Перед вами лист с четырехугольниками. Какие четырехугольники из изображенных на листе вы знаете? Для каких четырехугольников знаете точные определения и свойства? А какие известны по форме, но определения и свойств этих свойств не знаете? Да это квадрат и ромб, с понятием квадрата вы встречались ещё в начальной школе, да и ромб фигура- знакома.
Чтобы узнать их определения и свойства нам не обойтись без знаний полученных ранее. Мы их проверим, выполнив следующую работу. Возьмите лист № 1. На листе вопросы. Если вы согласны с предложением ставьте «да», если не согласны ставьте «нет». Ответы появятся на доске через 3 мин. Если появляются вопросы у учащихся, то на них отвечают или учащиеся или учитель. Приводятся примеры.
п/п
Вопрос
Данет
Является ли прямоугольником параллелограмм, у которого есть прямой угол?
Верно ли, что каждый прямоугольник является параллелограммом?
Верно ли, что каждый параллелограмм является прямоугольником?
Диагонали параллелограмма равны 4 и 5 дм. Является ли этот параллелограмм прямоугольником?
Диагонали четырехугольника равны. Обязательно ли этот четырехугольник прямоугольник?
6.
Верно ли, что в каждом четырехугольнике сумма углов составляет 3600.
7.
Верно ли, что в каждом четырехугольнике сумма соседних углов равна 1800
8.
Верно ли, что в каждом четырехугольнике противоположные углы равны.
III. Формирование новых знаний.
Сегодня Вам предстоит самостоятельно изучить новый материал. Сейчас откроете учебник на стр.109. Читая текст, вы делает пометки на полях: слайд 4
V – уже знал;
+ – новое;
– – думал иначе;
? – не понял, есть вопросы.
Затем вам предстоит заполнить таблицу, это лист №2. Записи делайте краткие, ключевые слова, фразы.
Лист №2
Определения
Свойства, особые свойства.
ромб
1.
2.
3.
4.
5.
6.
квадрат
1.
2.
3.
4.
5.
6.
Кстати: Ромб (от греч.) бубен. Если сейчас бубны делают круглой формы, то раньше их делали как раз в форме ромба. От тех времен дошли ромбики на картах.
После заполнения учащимися таблицы обобщаем результаты работы в режиме беседы. Даются определения, перечисляются свойства фигур (ромба, квадрата), находят общие свойства. Если у обучающихся возникли вопросы, то отвечаю на них, предварительно выяснив, не может ли кто-то из обучающихся ответить на возникший вопрос. ( Этот приём способствует развитию умения классифицировать, систематизировать поступающую информацию, выделять новое.)
Конечно, при решении задач на уроках так и в жизни используются свойства фигур.
Например: Ромб, в котором проведены диагонали, считается одной из самых крепких и выносливых конструкций. Такую конструкцию очень широко используют для постройки мостов, зданий, и даже, для рамы мотоцикла.
Вы выяснили, каким особым свойством обладают диагонали ромба, кроме того, что они точкой пересечения делятся пополам. Нам необходимо доказать это свойство. Работа в парах. Задача пар: прочитать доказательство, определить основную идею. Желающие доказывают у доски, остальные учащиеся следят за доказательством, задают вопросы.
IV. Применение знаний, формирование умений и навыков.
Теперь зная свойства ромба, решите задачу. Два ученика решают у доски.
Задача1 .
Найдите периметр ромба ABCD, если ∟ В =120 ◦, а диагональ BD = 20 см. (Ответ: 20 см) рис.на доске. Наводящие вопросы:
— Что называют периметром?
— Как найти периметр ромба?
— Каким свойством обладают диагонали ромба?
— Свойства равностороннего треугольника?
Задача 2. Найдите углы ромба, если его диагонали составляют с его стороной углы, один из которых на 300 меньше другого. Чертёж сделать самостоятельно. (Ответ: 300 и 600).
После решения идет обсуждение решённых задач.
V. Теоретическая самостоятельная работа.
— Заполните таблицу, отметив знаки + (да) и – (нет).
Лист № 3.
параллелограмм
прямоугольник
ромб
ввадрат
1.
Все стороны равны
2.
Все углы равны
3.
Противоположные стороны параллельны и равны
4.
Противоположные углы равны
5.
Сумма соседних углов равна 1800
6.
Все углы прямые
7.
Диагонали равны
8.
Диагонали пересекаются и точкой пресечения делятся пополам.
9.
Диагонали являются биссектрисами углов
10.
Диагонали взаимно перпендикулярны
параллелограмм
прямоугольник
ромб
квадрат
1.
Все стороны равны
_
_
+
+
2.
Все углы равны
_
+
+
3.
Противоположные стороны параллельны и равны
+
+
+
+
4.
Противоположные углы равны
+
+
+
+
5.
Сумма соседних углов равна 1800
+
+
+
+
6.
Все углы прямые
_
+
_
+
7.
Диагонали равны
_
+
_
+
8.
Диагонали пересекаются и точкой пресечения делятся пополам.
+
+
+
+
9.
Диагонали являются биссектрисами углов
_
_
+
+
10.
Диагонали взаимно перпендикулярны
_
_
+
+
Самостоятельную проверить и поставьте себе оценку.
Критерии выставления оценки:
Оценка «5» — все ответы верные.
Оценка «4» — допущены 1, 2 ошибки.
Оценка «3» — допущены 3-5 ошибки.
Оценка «2» — допущены более 5 ошибок.
VI. Домашнее задание: 1. п.п.47. Выучить определения и свойства ромба и квадрата. Уметь доказывать теорему, выражающую особое свойство ромба. №№ 406,407.
VII. Подведение итогов урока
Выставить оценки за работу на уроке наиболее активным учащимся и кто выполнил
работу по уровням.
VIII. Рефлексия.
Важна ли сегодняшняя тема урока. Если да, то обоснуйте.
Какие новые понятия изучили?
Что узнали нового и чему научились на уроке?
Чтобы хотели узнать ещё по данной теме?
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сумма внутренних углов любого четырехугольника равна (360^circ).
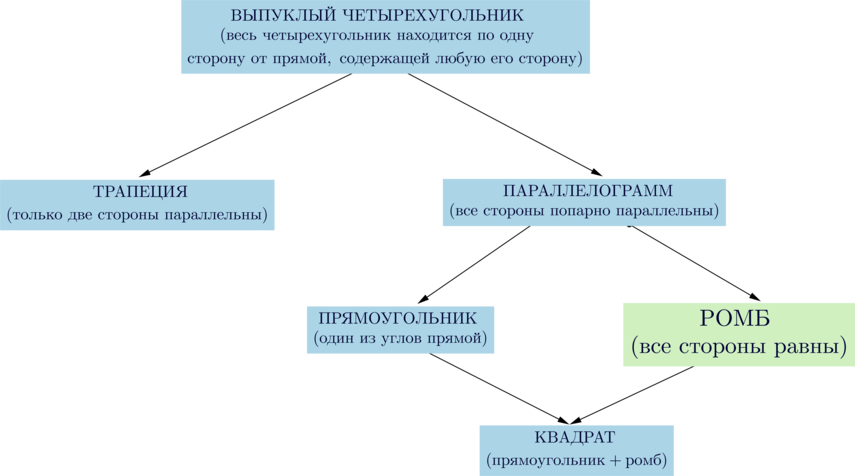
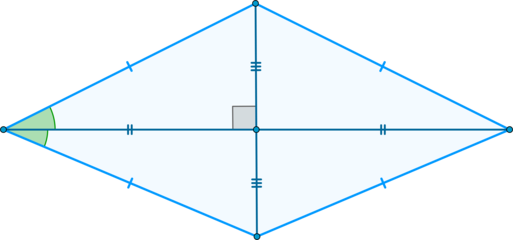
Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.

2. Площадь ромба равна половине произведения его диагоналей.

Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.

В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} — angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.

Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
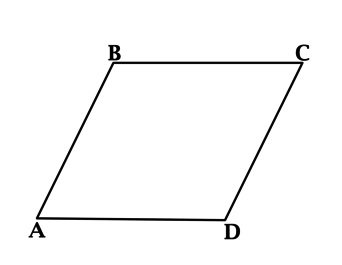
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
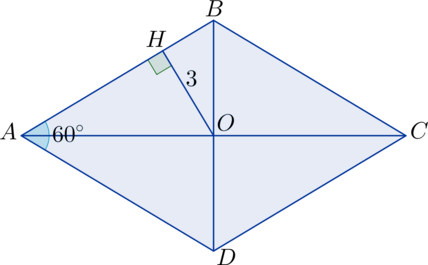
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
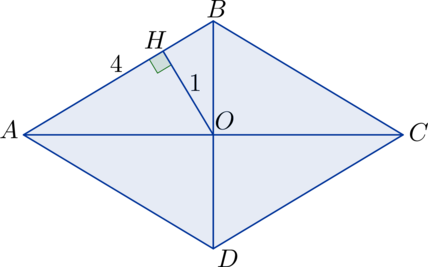
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 8).
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
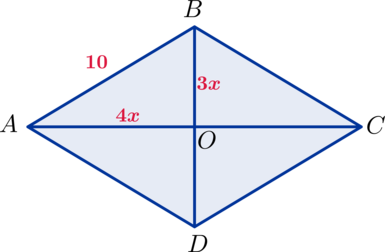
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ

Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
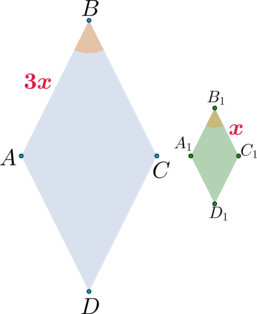
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.
