Что такое прямоугольник ромб квадрат какие свойства вы знаете

Предварительные сведения
Для начала разберемся с таким понятием, как параллелограмм.
Определение 1
Четырехугольником называется многоугольник, у которого $4$ вершины.
Четырехугольник имеет $4$ стороны, $4$ вершины и $4$ угла. Стороны, не имеющие общих вершин, называют противоположными сторона четырехугольника, в противном случае они называются смежными. Углы, не имеющие общих сторон, также называют смежными.
Введем теперь, непосредственно, определение параллелограмма.
Определение 2
Параллелограмм — это четырехугольник, в котором противоположные стороны параллельны между собой.
Напомним основные свойства параллелограмма.
Свойство 1: Противоположные стороны и углы параллелограмма равны, соответственно, между собой.
Свойство 2: Диагонали, проведенные в параллелограмме, делятся пополам их точкой пересечения.
Рассмотрим далее подробно понятия прямоугольника, ромба и квадрата.
Прямоугольник
Определение 3
Параллелограмм, у которого есть прямой угол, называется прямоугольником (рис. 1).

Рисунок 1. Прямоугольник
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Очевидно, что в прямоугольнике все четыре угла равняются ${90}^0$
Рассмотрим два свойства прямоугольника.
Свойство 3: Обе диагонали прямоугольника равны между собой.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$ (рис. 2). Докажем, что $AC=BD$.
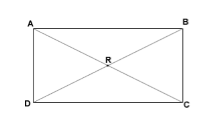
Рисунок 2.
Так как прямоугольник по определению $1$ является параллелограммом, то по свойству $1$ параллелограмма, имеем
Так как $angle B=angle A={90}^0$, а $AB$ — общая сторона, то по I признаку равенства треугольников, $triangle ABD=triangle ABC$. Следовательно
Свойство доказано.
Свойство 4 (признак прямоугольника): Если обе диагонали параллелограмма равны между собой, то он является прямоугольником.
Доказательство.
Пусть нам дан прямоугольник $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $R$ (рис. 2).
Из свойства $2$ параллелограмма и равенства его диагоналей, получим
Так как $angle DRC=angle ARB$, как вертикальные, то по $I$ признаку равенства треугольников $triangle DRC=triangle ARB$. Значит, $angle RDC=angle RCD=angle RAB={rm }angle RBA$.
Так как $angle DRA=angle CRB$, как вертикальные, то по I признаку равенства треугольников $triangle DRA=triangle CRB$. Значит, $angle RDA=angle RAD=angle RCB={rm }angle RBC$.
Следовательно, $angle A=angle B=angle C=angle D$.
Так как сумма углов четырехугольника равняется ${360}^0$, то
Значит, по определению $3$, $ABCD$ является прямоугольником.
Свойство доказано.
Ромб
Определение 4
Параллелограмм, у которого все его четыре стороны равны между собой, называется ромбом (рис. 3).
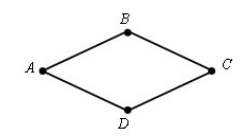
Рисунок 3. Ромб
Рассмотрим свойство ромба.
Свойство 5: Диагонали ромба являются биссектрисами его углов и перпендикулярны друг другу.
Доказательство.
Пусть нам дан ромб $ABCD$. Проведем в нем диагонали $AC$ и $BD$. Пусть они пересекаются в точке $E$ (рис. 4).
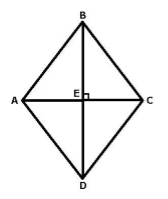
Рисунок 4.
Так как ромб является прямоугольником с равными сторонами, то
Следовательно, по третьему признаку равенства треугольников,
Это доказывает, что диагонали являются биссектрисами углов ромба.
Так как $AB=AD$, то треугольник $ABD$ равнобедренный, а так как $AE$ — медиана треугольника $ABD$, то $AC$ перпендикулярно $BD$.
Свойство доказано.
Квадрат
Прямоугольник, у которого все его четыре стороны равны между собой, называется квадратом (рис. 5).

Рисунок 5. Квадрат
Очевидно, что квадрат — частный случай ромба. Следовательно, квадрат обладает всеми свойствами прямоугольника и ромба.
Пример задачи
Пример 1
Найти периметр квадрата, диагональ которого равняется $10$.
Решение.
Обозначим сторону квадрата через $a$. Тогда, по теореме Пифагора
[a^2+a^2=100] [{2a}^2=100] [a^2=50] [a=5sqrt{2}] [P=4a=20sqrt{2}]
Ответ: $20sqrt{2}$.
Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».
СОДЕРЖАНИЕ СТАТЬИ
1. Параллелограмм
Сложное слово «параллелограмм»? А скрывается за ним очень простая фигура.
Смотри:
 | Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны |
Ну, то есть, взяли две параллельные прямые:

Пересекли ещё двумя:

И вот внутри – параллелограмм!
Какие же есть свойства у параллелограмма?
Свойства параллелограмма.
То есть, чем можно пользоваться, если в задаче дан параллелограмм?
На этот вопрос отвечает следующая теорема:
В любом параллелограмме:
- Противоположные стороны равны
- Противоположные углы равны
- Диагонали делятся пополам точкой пересечения
Давай нарисуем все подробно.
Что означает первый пункт теоремы? А то, что если у тебя ЕСТЬ параллелограмм, то непременно
 | и . |
Второй пункт означает, что если ЕСТЬ параллелограмм, то, опять же, непременно:
 | и |
Ну, и наконец, третий пункт означает, что если у тебя ЕСТЬ параллелограмм, то обязательно:
 | и |
Видишь, какое богатство выбора? Что же использовать в задаче? Попробуй ориентироваться на вопрос задачи, или просто пробуй все по очереди – какой-нибудь «ключик» да подойдёт.
А теперь зададимся другим вопросом: а как узнать параллелограмм «в лицо»? Что такое должно случиться с четырехугольником, чтобы мы имели право выдать ему «звание» параллелограмма?
На этот вопрос отвечает несколько признаков параллелограмма.
Признаки параллелограмма.
Внимание! Начинаем.
- Признак 1. Если у четырехугольника две стороны равны и параллельны, то это – параллелограмм.
 | ; — параллелограмм. |
— паралелограмм.
- Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 3. Если у четырехугольника противоположные углы равны, то это – параллелограмм.
 | ; – параллелограмм. |
- Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
Обрати внимание: если ты нашёл хотя бы один признак в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

2. Прямоугольник
Думаю, что для тебя вовсе не явится новостью то, что
 | Прямоугольник – четырехугольник, все углы которого прямые. |
Первый вопрос: а является ли прямоугольник параллелограммом?
Конечно, является! Ведь у него и — помнишь, наш признак 3?
А отсюда, конечно же, следует, что у прямоугольника, как и у всякого параллелограмма и , а диагонали точкой пересечения делятся пополам.
Но есть у прямоугольника и одно отличительноесвойство.
Свойство прямоугольника
 | Диагонали прямоугольника равны: . |
Почему это свойство отличительное? Потому что ни у какого другого параллелограмма не бывает равных диагоналей. Сформулируем более чётко.
 | Если у параллелограмма равны диагонали, то это — прямоугольник. |
Обрати внимание: чтобы стать прямоугольником, четырехугольнику нужно сперва стать параллелограммом, а потом уже предъявлять равенство диагоналей.
3. Ромб
 | Ромб – четырехугольник, все стороны которого равны между собой. |
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него и (вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
- Свойство 1. Диагонали ромба перпендикулярны.
 | (если ты забыл, напомню: — значок перпендикулярности) |
- Свойство 2. Диагонали ромба являются биссектрисами его углов.
Посмотри на картинку:

Как и в случае с прямоугольником, свойства эти – отличительные, то есть по каждому из этих свойств можно заключить, что перед нами не просто параллелограмм, а именно ромб.
Признаки ромба
- Признак 1. Если в параллелограмме диагонали перпендикулярны, то это ромб.

- Признак 2. Если в параллелограммехотя бы одна из диагоналей делит пополам оба угла, через которые она проходит, то этот параллелограмм – ромб.

И снова обрати внимание: должен быть не просто четырехугольник, у которого перпендикулярны диагонали, а именно параллелограмм. Убедись:
 | разве это ромб? |
Нет, конечно, хотя его диагонали и перпендикулярны, а диагональ – биссектриса углов и . Но … диагонали не делятся, точкой пересечения пополам, поэтому – НЕ параллелограмм, а значит, и НЕ ромб.
4. Квадрат
 | Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые. |
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
 | У квадрата угол между диагональю и стороной равен . |
Понятно почему? Квадрат — ромб – биссектриса угла A, который равен . Значит делит (да и тоже) на два угла по .
 | Диагонали квадрата равны, перпендикулярны и делятся точкой пересечения пополам. |
Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще – параллелограмм диагонали делятся точкой пересечения пополам.
 | Если сторона квадрата равна , то его диагональ равна . |
Почему? Ну, просто применим теорему Пифагора к .
Значит, .
СРЕДНИЙ УРОВЕНЬ
Свойства четырехугольников. Параллелограмм
Параллелограмм – это четырехугольник, противоположные стороны которого попарно параллельны.

Свойства параллелограмма
Внимание! Слова «свойства параллелограмма» означают, что если у тебя в задаче есть параллелограмм, то всем нижеследующим можно пользоваться.
Итак,
Теорема о свойствах параллелограмма.
В любом параллелограмме:
Давай-ка поймём, почему это всё верно, иными словами ДОКАЖЕМ теорему.
Итак, почему верно 1)?
 | Давай проведём диагональ . Что получится? Два треугольника: и . |
Раз – параллелограмм, то :
- как накрест лежащие
- как накрест лежащие.
Значит, (по II признаку: и — общая.)
Ну вот, а раз , то и – всё! – доказали.
Но кстати! Мы ещё доказали при этом и 2)!
Почему? Но ведь (смотри на картинку), то есть , а именно потому, что .
Осталось только 3).
Для этого всё-таки придётся провести вторую диагональ.
 | Мы уже выяснили, что . Давай снова отметим равные накрест лежащие углы (посмотри и убедись, что все верно). |
И теперь видим, что — по II признаку ( угла и сторона «между» ними).
 | Значит, (напротив углов и ) и (напротив углов и соответственно). |
Свойства доказали! Перейдём к признакам.
Признаки параллелограмма
Напомним, что признак параллелограмма отвечает на вопрос «как узнать?», что фигура является параллелограммом.
Признак 1. Если у четырехугольника две стороны равны и параллельны, то это параллелограмм.
В значках это так:
 | ; – параллелограмм. |
Почему? Хорошо бы понять, почему – этого хватит. Но смотри:
 | по 1 признаку: , — общая и как накрест лежащие при параллельных и и секущей . |
А раз ,
 | то (лежат напротив и соответственно). Но это значит, что ( и — накрест лежащие и оказались равны). |
Ну вот и разобрались, почему признак 1 верен.
Признак 2. Если у четырехугольника противоположные стороны равны, то это – параллелограмм.
 | , – параллелограмм. |
Ну, это ещё легче! Снова проведём диагональ .
 | Теперь просто по трём сторонам. |
А значит:
 | и , то есть – параллелограмм. |
Признак 3. Если у четырёхугольника противоположные углы равны, то это – параллелограмм.
 | , – параллелограмм. |
И тоже несложно. Но …по-другому!
 | (ведь – четырехугольник, а , по условию). |
Значит, . Ух! Но и – внутренние односторонние при секущей !
Поэтому тот факт, что означает, что .
А если посмотришь с другой стороны, то и – внутренние односторонние при секущей ! И поэтому .
Видишь, как здорово?!
Признак 4. Если у четырехугольника диагонали делятся точкой пересечения пополам, то это – параллелограмм.
 | ; – параллелограмм. |
И опять просто:
 | , как вертикальные , , и . |
Точно так же , , и .
Обрати внимание: если ты нашел хотя бы один признак параллелограмма в своей задаче, то у тебя точно параллелограмм, и ты можешь пользоваться всеми свойствами параллелограмма.
Для полной ясности посмотри на схему:

Свойства четырехугольников. Прямоугольник.
 | Прямоугольник – четырехугольник, все углы которого прямые. |
Свойства прямоугольника:
- Прямоугольник – параллелограмм
- Диагонали прямоугольника равны
Пункт 1) совсем очевидный – ведь просто выполнен признак 3 ( )
А пункт 2) – очень важный. Итак, докажем, что
диагонали прямоугольника равны.
 | Раз прямоугольник – это параллелограмм, то . |
А значит, по двум катетам ( и — общий).
Ну вот, раз треугольники и равны, то у них и гипотенузы и тоже равны.
Доказали, что !
И представь себе, равенство диагоналей – отличительное свойство именно прямоугольника среди всех параллелограммов. То есть верно такое утверждение^
Если у параллелограмма равны диагонали, то это прямоугольник.
Давай поймём, почему?
 | – параллелограмм – по условию. – теперь уже по трём сторонам. |
Значит, (имеются в виду углы параллелограмма). Но ещё раз вспомним, что – параллелограмм, и поэтому .
Значит, . Ну и, конечно, из этого следует, что каждый из них по ! Ведь в сумме-то они должны давать !
Вот и доказали, что если у параллелограмма вдруг (!) окажутся равные диагонали, то это точно прямоугольник.
Но! Обрати внимание! Речь идёт о параллелограммах! Не любой четырехугольник с равными диагоналями – прямоугольник, а только параллелограмм!
Свойства четырехугольников. Ромб
 | Ромб – четырехугольник, все стороны которого равны между собой. |
И снова вопрос: ромб – это параллелограмм или нет?
С полным правом – параллелограмм, потому что у него и (Вспоминаем наш признак 2).
И снова, раз ромб – параллелограмм, то он обязан обладать всеми свойствами параллелограмма. Это означает, что у ромба противоположные углы равны, противоположные стороны параллельны, а диагонали делятся точкой пересечения пополам.
Но есть и особенные свойства. Формулируем.
Свойства ромба
Свойство 1. Диагонали ромба перпендикулярны.
Почему? Ну, раз ромб – это параллелограмм, то его диагонали делятся пополам.
 | Поэтому по трём сторонам ( , — общая, ).И значит, , но они смежные! и . |
Свойство 2. Диагонали ромба являются биссектрисами его углов.
Почему? Да, потому же!
 | Из-за того, что диагонали делятся точкой пересечения пополам, а все стороны ромба равны, весь ромб оказался разделён диагоналями на четыре равных треугольника: . |
Поэтому
Иными словами, диагонали и оказались биссектрисами углов ромба.
Как в случае с прямоугольником, свойства эти – отличительные, каждые из них является ещё и признаком ромба.
Признаки ромба.
Признак 1. Если в параллелограмме диагонали перпендикулярны то это – ромб.
 | — ромб |
Почему? Смотри:
 | — параллелограмм . Но ещё дано, что — по двум катетам. И значит, – и всё! |
Признак 2. Если в параллелограмме хотя бы одна из диагоналей делит пополам оба угла, через которые она проходит, то этот параллелограмм – ромб.
А это почему? А посмотри,
 | , так как – параллелограмм. Но ещё дано, что – биссектриса углов и . |
Значит, и оба этих треугольника – равнобедренные.
 | Значит, , то есть — ромб. |
И снова обрати внимание! Не всякий четырёхугольник с перпендикулярными диагоналями – ромб.
Вот пример:
 | Это вовсе не ромб, хоть его диагонали и перпендикулярны. |
Чтобы быть ромбом, четырёхугольник сперва должен «стать» параллелограммом, а потом уже демонстрировать признак 1 или признак 2.
Свойства четырехугольников. Квадрат
 | Квадрат – четырехугольник, у которого все стороны равны между собой, а все углы – прямые. |
То есть квадрат – это прямоугольник и ромб одновременно. Давай посмотрим, что из этого получится.
 | У квадрата угол между диагональю и стороной равен . |
Понятно, почему? Квадрат — ромб – биссектриса угла , который равен . Значит делит (да и тоже) на два угла по .
 | Диагонали квадрата – равны, перпендикулярны и делятся точкой пересечения пополам. |
Ну, это совсем ясно: прямоугольник диагонали равны; ромб диагонали перпендикулярны, и вообще – параллелограмм диагонали делятся точкой пересечения пополам.
 | Если сторона квадрата равна , то его диагональ равна . |
Почему? Ну, просто применим теорему Пифагора к .
Значит,
КРАТКОЕ ИЗЛОЖЕНИЕ И ОСНОВНЫЕ ФОРМУЛЫ
 |
|
Свойства параллелограмма:
- Противоположные стороны равны: , .
- Противоположные углы равны: , .
- Углы при одной стороне составляют в сумме : , , , .
- Диагонали делятся точкой пересечения пополам: .
 |
|
Свойства прямоугольника:
- Диагонали прямоугольника равны: .
- Прямоугольник – параллелограмм (для прямоугольника выполняются все свойства параллелограмма).
 |
|
Свойства ромба:
- Диагонали ромба перпендикулярны: .
- Диагонали ромба являются биссектрисами его углов: ; ; ; .
- Ромб – параллелограмм (для ромба выполняются все свойства параллелограмма).
 |
|
Свойства квадрата:
Квадрат — ромб и прямоугольник одновременно, следовательно для квадрата выполняются все свойства прямоугольника и ромба. А так же:
 |
|
ОСТАВШИЕСЯ 2/3 СТАТЬИ ДОСТУПНЫ ТОЛЬКО УЧЕНИКАМ YOUCLEVER!
Стать учеником YouClever,
Подготовиться к ОГЭ или ЕГЭ по математике по цене «чашка кофе в месяц»,
А также получить бессрочный доступ к учебнику «YouClever», Программе подготовки (решебнику) «100gia», неограниченному пробному ЕГЭ и ОГЭ, 6000 задач с разбором решений и к другим сервисам YouClever и 100gia.
