В каких равенствах применяли следующие свойства распределительные
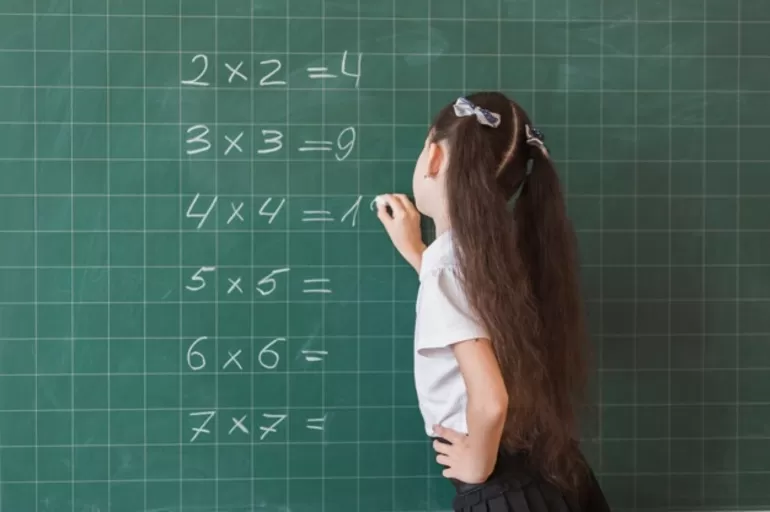
Илья Маслюков · 15 ноября 2018
8,4 K
Выпускник экономического вуза, мама двоих детей, фрилансер, таролог в пути)…
Распределительное свойство умножения выглядит так:
(a+b)*c=ac+bc
(a-b)*c=ac-bc
Для того, чтобы умножить сумму на число, можно каждое слагаемое умножить на это число и полученные произведения сложить.
Для того, чтобы умножить разность на число, можно уменьшаемое и вычитаемое умножить на это число и из первого произведения вычесть второе.
Чтобы умножить число на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные результаты сложить.
С помощью букв распределительное свойство умножения относительно сложения записывают так:
a*(b+c)=a*b+a*c
либо так:
(b+c)*a=a*b+a*c
Для чего используется фигурная скобка?
Мои интересы: разнообразны, но можно выделить следующие: литература, история…
Фигурные скобки используются в математике для обозначения операции взятия дробной части; приоритета операций, как третий уровень вложенности (после круглых и квадратных скобок); для обозначения множеств. Также в математике и классической механике фигурными скобками обозначается оператор специального вида, называемый скобками Пуассона. В программировании фигурные скобки являются или операторными (Си, C++, Java, Perl и PHP), или комментарием (Паскаль), могут также служить для образования списка (в Mathematica), анонимного хеш-массива (в Perl, в иных позициях для доступа к элементу хеша), словаря (в Python) или множества (Сетл).
Существует ли какое-то доказательство того, почему работает закон умножения а*б=б*а (где а и б — действительные числа), или это принимается как аксиома?
На самом деле может быть и так, и так. Умножение можно определить двумя способами. 1) существует такая аксиоматика Пеано, которая сначала определяет, что такое натуральные числа и ноль и вводит для них две операции: сложения и умножения. Умножение определяется сначала для нуля a*0=0, а затем индуктивно для всех n: a*(n+1)=a*n+a. После аксиом и определений начинаются теоремы, где доказывается коммутативность a•b=b•a для натуральных чисел с нулем. Делается это методом математической индукции. Но это лишь для натуральных. Затем опреледляются целые числа (добавили отрицательных). Для них расширяется понятие сложения и умножения, и снова доказываются все теоремы, включая коммутативность умножения, но уже для целых. Это не всё. Теперь очередь рациональных чисел. Снова определение умножения и сложения и снова доказательство новой расширенной операции, что она коммутативна. Следующими приходят на очередь действительные числа как множество пополнения (фундаментальные последовательности и все такое, если нужны подробности) для рациональных. И да, снова расширение для сложения и умножения, снова доказательство коммутативности. Далее можно продолжить на комплексные. 2) Но есть и другой подход. Действительные числа определяются как непрерывное упорядоченное поле, то есть задаются аксиомы поля (Группа коммутативная по сложению, Группа коммутативная по умножению без нуля, дистрибутивность), аксиомы упорядоченности (например, что из a < b следует a + c < b + c), и аксиома непрерывности Дедекинда (что если элементы множества A целиком меньше или равны элементам множества B, то есть число, которое больше или равно любого элемента A, а также меньше или равно любого элемента B). И вот в такой системе аксиом коммутативность умножения a•b=b•a является аксиомой: без нуля все числа являются коммутативной группой по умножению, а, значит, операция умножения коммутативна из определения коммутативной группы. И да, существует теорема, которая доказывает, что такое непрерывное упорядоченное поле может быть только одно и оно совпадает с тем, что дают нам аксиомы Пеано и все последующее их обобщения до действительных чисел (более формально: они изоморфны относительно сложения, умножения и упорядоченности)
Итого, если действительные числа — это расширение натуральных-целых-рациональных, то a•b=b•a — теорема. Если действительные числа — это поле, то a•b=b•a — аксиома
P. S. Комплексные числа и в той, и в той аксиоматике определяются как расширение действительных одинаково. Заново в них определяется умножение. Но его коммутативность доказать несложно, используюя коммутативность умножения действительных чисел.
Прочитать ещё 4 ответа
Как ЭВМ выполняет математические вычисления(например-умножение, деление)?
мои ответы не являются «глубокомысленными» статьями для ЯДзен
Ничего особенно сложного.
0*0, 0*1, 1*1 — нет проблем умножать?
Также как и сложение, такие операции можно делать даже механическим устройством. Рычажками переключающимися. Эти операции умели осуществлять и механические арифмометры.
Значит просто переводим число в двоичную систему и умножаем. Умножаем «в столбик», т.е. по разрядам.
Как работает метод Карацубы для умножения чисел?
Помните, как в школе умножали «столбиком»? Скажем, числа 52 и 37 умножают так:
Умножение двузначных чисел мы свели 1) к умножению однозначных (оно короткое), 2) к сложению, 3) и еще к сдвигу, эта операция настолько проста, что мы её и не замечаем. Она соответствует умножению на степень десятки, и «почти бесплатна»:
(50+2)×(30+7) = 5×3×100 + 2×3×10 + 5×7×10 + 2×7.
Умножение двух двузначных чисел требует четырех коротких умножений.
Умножение двух трехзначных чисел требует девяти коротких умножений.
И так далее.
Умножение двух N-значных чисел сводится к N² коротким умножениям (и ещё к сложениям и сдвигам).
Для компьютерных вычислений умножение – самая затратная по времени операция, а сложение и тем более сдвиг – нет; поэтому сложность алгоритма умножения длинных чисел оценивают числом коротких, «однозначных» умножений. (Внутри компьютера числа представляются не так, как в школьных тетрадках, основание счисления будет не 10, а какая-то степень двойки, но для оценки это непринципиально.)
Анатолий Карацуба в 1960 году он придумал алгоритм, который работает быстрее.
Чтобы сосчитать (50+2)×(30+7), метод Карацубы требует только три коротких произведения: 5×3, 2×7 и (5+2)×(3+7).
Через них получается выражение для
2×3 + 5×7=(5+2)×(3+7)- 5×3-2×7.
А это все, что нужно знать, чтобы вычислить произведение:
(50+2)×(30+7) = 5×3×100 + (2×3 + 5×7)×10 + 2×7.
Нам потребовалось не N² операций, а только
Как это бывает в математике, после первого шага началась гонка за наилучшим результатом. Всегда приятно поставить рекорд: найти больше всех цифр числа π или самое большое простое число.
Немецкие математики Арнольд Шёнхаге и Фолькер Штрассен в 1971 году придумали, как использовать быстрое преобразование Фурье, чтобы умножать большие числа еще быстрее. Они свели задачу умножения чисел к задаче умножения многочленов, и применили к таким функциям быстрое преобразование Фурье. (По версии журнала Computing in Science & Engineering БПФ – один из 10 важнейших алгоритмов ХХ столетия.) Теперь можно было умножать за
операций. И в XX веке все компьютеры так и умножали. Но теперь существуют алгоритмы ещё шустрее
Почему сначала делается умножение, а потом сложение? Как это можно объяснить?
Студент, будущий математик, программист, повар и просто фанат гугла
Потому, что стоит вспомнить, что это такое — умножение. Под этой операцией скрывается сложение одного и того же числа несколько раз. Делая сначала сложения, мы меняет это самое «количество раз». Вот вам пример:
7*3+5=7+7+7+5=7+7+12=7*2+12
А вот если бы мы делали сначала сложение, получилось бы следующее:
7*3+5=>7*8=7+7+7+7+7+7+7+7
Разные вещи, не находите?
Прочитать ещё 2 ответа
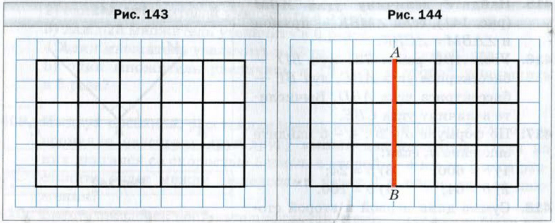
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.
Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).
Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
abc = cba,
17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).
На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).
Равенсто 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
ab + ac = a(b + c).
Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:
P = 2(a + b).
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b − c) = ab − ac
Пример 1. Вычислите удобным способом:
1) 25 * 867 * 4;
2) 329 * 75 + 329 * 246.
Решение.
1) Используем переместительное, а затме сочетательное свойства умножения:
25 * 867 * 4 = 867 * (25 * 4) = 867 * 100 = 86 700.
2) Имеем:
329 * 754 + 329 * 246 = 329 * (754 + 246) = 329 * 1 000 = 329 000.
Пример 2. Упростите выражение:
1) 4a * 3b;
2) 18m − 13m.
Решение.
1) Используя переместительное и сочетательное свойства умножения, получаем:
4a * 3b = (4 * 3) * ab = 12ab.
2) Используя распределительное свойство умножения относительно вычитания, получаем:
18m − 13m = m(18 − 13) = m * 5 = 5m.
Пример 3. Запишите выражение 5(2m + 7) так, чтобы оно не содержало скобок.
Решение.
Согласно распределительному свойству умножения относительно сложения имеем:
5(2m + 7) = 5 * 2m + 5 * 7 = 10m + 35.
Такое преобразование называют раскрытием скобок.
Пример 4. Вычислите удобным способом значение выражения 125 * 24 * 283.
Решение. Имеем:
125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8) * (3 * 283) = 1 000 * 849 = 849 000.
Пример 5. Выполните умножение: 3 сут 18 ч * 6.
Решение. Имеем:
3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.
При решении примера было использовано распределительное свойство умножения относительно сложения:
3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.
- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a,
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42;
4 · 2 · 3 = 3 · 2 · 4 = 24.
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c),
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30.
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500.
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500,
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b,
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m.
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a — b) = m · a — m · b.
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a — b) · m = a · m — b · m.
Переход от умножения:
m · (a + b) и m · (a — b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a — m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a — m · b
к умножению:
m · (a + b) и m · (a — b)
называется вынесением общего множителя за скобки.
Краткое описание
Используемый в школе распределительный закон умножения позволяет ученикам максимально быстро выполнить все необходимые вычисления. Знание определенных нюансов поможет решить сложные уравнения и различные задачи. Процесс умножения представляет собой сокращенный процесс сложения. А это означает, что первый множитель выступает в роли числа, которое складывается само с собой определенное количество раз, соответствующее второму множителю. Пример: 4 * 8 = 4+4+4+4+4+4+4+4 = 32.

Элементарное математическое умножение было изобретено в то время, когда у человечества возникла необходимость выполнять большие вычисления, которые просто неудобно записывать в виде элементарного сложения. Всем хорошо известно, что можно 8 раз сложить число 4, а можно 4 раза сложить число 8, но итоговый результат от этого не поменяется. Именно в этом и состоит смысл переместительного умножения всех задействованных элементов. Умножение позволило человеку решить довольно много проблем, но вместе с этим в алгебру пришло и деление, но уже как противоположная математическая операция.
Ключевые особенности
Чтобы даже на начальном этапе ученик мог выполнить умножение суммы некоторых чисел, необходимо просто умножить каждое слагаемое по отдельности и сложить полученный результат. К примеру: (j + d) * s = sj + sd либо s * (j + d) = sj + sd. Чтобы немного упростить способ решения задачи, описанное правило можно использовать в обратном порядке: s * j + s * d = s * (j + d). В этом случае общий множитель выносится за пределы скобок.
Если попробовать задействовать многофункциональное распределительное свойство сложения, то в итоге можно будет решить следующие математические примеры:

- Классическая задача: 35 * 6. Следует представить число 35 как сумму двух чисел 30 и 5, которую просто нужно перемножить на 6: (30 + 5) * 6. Все вычисления выполняются элементарно: 30 * 6 + 5 * 6 = 210.
- Еще один пример: 4 * (20 + 13). Для решения нужно умножить число 4 на каждое задействованное слагаемое: 4 * 20 + 4 * 13. Сложение примет следующий вид: 80 + 52 = 132.
- Также следует рассмотреть более сложный пример: 8 * (45 — 3). Необходимо перемножить на число 9 уменьшаемое 45, а также вычитаемое 3. Пример: 8 * 45 — 8 * 3. Если все сделать верно, то итоговый результат примет следующий вид: 360 — 24 = 336.
Умелое применение распределительного свойства умножения поможет избежать распространенных ошибок. Так, основное правило актуально не только по отношению к сумме, но и к разности двух и более выражений. Для укрепления полученных навыков можно попробовать самостоятельно придумать задачу.
Основные математические возможности
Чтобы можно было выполнить определенные арифметические действия по отношению к числу, необходимо поочередно умножить его на каждое слагаемое и в итоге сложить полученные произведения. А это значит, что для любых частных чисел l, r, w верным будет следующее равенство: w * (l + r) = w * l + w * r. Этот пример отлично выражает распределительный закон сложения и последующего умножения. Так как число и сумма являются множителями, то после смены их места расположения, задействовав для этого переместительное свойство, можно будет сформировать наиболее подходящее свойство.
Всего специалисты выделяют три свойства распределительного умножения:
- Элементарное сочетательное. Именно это свойство применяется для тех примеров, где используется минимум 3 множителя. Основная мысль сочетательного свойства в том, что можно легко перемножить первые два множителя, а только потом умножить результат на третий множитель. Стоит учесть, что порядок перемножения может быть абсолютно любым.
- Переместительное. Произведение не меняется от перемены мест множителя. Для примера из двух множителей это свойство не является критичным, но для заданий с тремя и более множителями это направление может сэкономить много свободного времени.
- Распределительное. В математике это свойство получило большой спрос для умножения числа на сумму либо разность. Распределительный подход сокращает время решения задачи при правильном подходе. Суть свойства в том, что во время умножения числа на разность либо конкретную сумму можно каждое слагаемое умножить на основное число, а уже потом выполнить сложение.

Все перечисленные направления имеют свои особенности и правила использования на практике, которые обязательно нужно учесть для лучшего усвоения этой темы.
Правила вычитания
Умножение и последующее вычитание натуральных чисел обязательно связывается распределительным свойством. Учащимся обязательно нужно запомнить формулировку этого правила: умножить определенную разность двух рациональных чисел на конкретное число — это вычитание из произведения уменьшаемого числа произведения данного или неизвестного вычитаемого числа. Все математические примеры записываются при помощи обычных букв: (s — r)* n = s * n — r * n. Задействованными символами могут называться определенные рациональные целые и дробные числа.

Элементарные примеры распределительного свойства умножения позволяют ученикам освоить технику решения распространенных математических задач. Если необходимо убедиться в равенстве уравнения 5 * (8 — 3) = 5 * 8 — 5 * 3, тогда нужно выполнить несколько арифметических действий. Так как пример 8 − 3 всегда равен 5, то произведение 5 * (8 — 3) всегда будет иметь следующий результат: 5 * 5 = 5+5+5+5+5=25. Теперь нужно вычислить разность между 5 * 8 и 5 * 3. Решение выглядит следующим образом: 5 * 8 − 5 * 3 = (5+5+5+5+5+5+5+5) — (5+5+5) = 40 — 15 = 25. Это значит, что равенство 5 * (8 − 3) = 5 * 8 − 5 * 3.
Использование двух и более слагаемых
Распространенное в алгебре распределительное свойство элементарного умножения активно применяется не только по отношению к двум слагаемым, но и для неограниченного количества арифметических элементов. Этот подход можно применить для всех форм дробей, что очень удобно. Стандартная формула имеет следующий вид:
- d x (e + t + h) = d x e + d x t + d x h .
- d x (e — t — h) = dxe — dxt — dxh.

В качестве примера следует рассмотреть следующее уравнение: 678 * 4. Чтобы понять все нюансы, надо представить число 678 как сумму трех чисел: 600, 70 и 8. Если это сделать, то в итоге можно получить следующее решение: (600 + 70 + 8) * 4 = 600 * 4 + 70 * 4 + 8 * 4 = 2400 + 280 + 32 = 2712. Для более быстрого решения задачи нужно упростить несколько выражений, используя для этого упомянутое ранее свойство.
Если в качестве примера взять уравнение 8 * (4х + 3у), тогда первым делом раскрывают имеющиеся скобки, применяя для этого распределительный закон умножения: 8 * 4х + 8 * 3у = 32х + 24у. Конечно, полученный результат сложить просто невозможно, так как заявленные слагаемые не являются подобными, к тому же они имеют разную буквенную часть. Именно поэтому ответ будет выглядеть следующим образом: 32х + 24у.
Если ученик научится использовать при решении различных примеров универсальное распределительное свойство сложения и умножения, то в итоге он сможет легко решать даже самые сложные математические примеры, так как многие ситуации можно свести к устному счету. Также будет существенно экономиться время при решении многоуровневых задач. Благодаря полученным знаниям, можно будет с легкостью упростить выражения. Эксперты рекомендуют дважды проверять выполненную работу, так как только в этом случае можно будет избежать ошибок.
Умножение нуля
Несмотря на то что ноль не относится к категории естественных чисел, этому направлению тоже нужно уделить повышенное внимание. Это связано с тем, что такое свойство используется во время умножения натуральных чисел столбиком. Если строго соблюдать смысл умножения, тогда произведение 0 * х, где х выступает в роли произвольного естественного числа больше единицы, представляет собой сумму х слагаемых. В такой ситуации актуальной является следующая формула: 0 * х = 0+0+0+0+….+0. Свойства математического сложения позволяют специалистам утверждать, что последняя сумма неизбежно будет равна нулю.
Чтобы иметь возможность сохранить справедливость элементарного умножения используемого числа на единицу, можно считать верным следующее равенство: 0 * 1 = 0. Это значит, что для любого естественного числа х выполняется равенство 0 * х = 0. Чтобы оставалось актуальным переместительное свойство умножения, нужно помнить о справедливости равенства х * 0 = 0 для всех натуральных чисел х.

Произведение естественного числа и нуля равно нулю 0 * х = 0, а также х * 0 = 0. Используемый x представляет собой произвольное натуральное число. Экспертами было доказано, что последнее утверждение играет важную роль формулировки свойства умножения ранее полученного числа и нуля. К примеру, произведение чисел 87 и 0 равно нулю. Если попробовать умножить 0 на 897689, то в итоге тоже получим ноль.
Распределительное свойство относительно разности
Правильное решение математических уравнений возможно только в том случае, если ученик предварительно хорошо изучил теоретическую часть этой темы. Чтобы выполнить элементарное умножение разности на число, необходимо предварительно умножить на него уменьшаемое, а только после этого — вычитаемое, и выполнить вычисление полученных результатов. Пример: g x (y — u) = g x y — g x u или (y — u) x g = g x y — g x u .
Понять все нюансы помогут следующие три примера:

- Для решения уравнения 78 * (12 — 5) принято использовать распределительный закон. Первым делом умножают 78 на оба числа: 78 * 12 — 78 * 5. Необходимо отыскать разность полученных значений: 936 — 390 = 546 и записать полученный результат. Ответ: 546.
- Следующий пример: 78 * 5. Нужно найти значение математического выражения, используя для этого ранее изученные свойства. Следует представить 78 как разность двух чисел 83 и 5. Решение будет выглядеть следующим образом: 78 * 5 = (83 − 5) * 5 = 83 * 5 − 5 * 5 = 390.
- Еще один арифметический пример: 9 * (2 + 30). Решение этого уравнения довольно простое: 9 * 2 + 9 * 30 = 18 + 270 = 288.
Решать такие задачи элементарно и быстро, но для этого нужно хорошо усвоить все правила, а также рекомендации специалистов, так как только в этом случае можно будет избежать грубых ошибок.
Манипуляции с натуральным числом
Этот раздел связан с умножением единицы на конкретное число. Если следовать смыслу умножения, то в итоге произведение изучаемого арифметического выражения х будет равно сумме х слагаемых, каждое из которых тоже равно единице. Действует элементарная формула: 1 * х = 1+1+1+….+1 = х. Пример: произведение чисел 1 и 78 равно 78, а результатом умножения 1 и 456 есть число 456.

Произведение х * 1 лишено какого-либо смысла, так как это арифметическое выражение представляет собой сумму одного слагаемого, которое равно число х, но сложение определяют для двух и более слагаемых. Чтобы сохранить справедливое переместительное свойство поэтапного умножения, нужно считать верным равенство х * 1 = х.
Опытные математики утверждают, что произведение двух разных чисел, одно из которых приравнивается к нулю, равно другому числу. Это утверждение выступает в качестве официальной формулировки умножения единицы и определенного числа. При помощи букв это свойство записывается так: 1 * х = х * 1 = х. За основу могут использоваться любые натуральные числа.
Многим может показаться, что сегодня нет необходимости разбираться во всех свойствах распределительного умножения, так как под рукой всегда есть калькулятор. Но даже у программ существуют свои ограничения, что просто недопустимо в банковской отрасли и правительственных отраслях. Именно поэтому бухгалтеры в обязательном порядке изучают все особенности применения распределительного закона умножения.