В каких равенствах применяли следующие свойства
После получения общих сведений о равенствах в математике переходим к более узким темам. Материал этой статьи даст представление о свойствах числовых равенств.
Что такое числовое равенство
Первый раз мы сталкиваемся с числовыми равенствами еще в начальной школе, когда происходит знакомство с числами и понятием «столько же». Т.е. самые примитивные числовые равенства это: 2=2, 5=5 и т.д. И на том уровне изучения мы называли их просто равенствами, без уточнения «числовые», и закладывали в них количественный или порядковый смысл (который несут натуральные числа). Например, равенство 2=2 будет соответствовать изображению, на котором – два цветка и на каждом сидит по две шмеля. Или, к примеру, две очереди, где вторыми по порядку стоят Вася и Ваня.
По мере появления знаний об арифметических действиях числовые равенства становятся сложнее: 5+7=12; 6-1=5; 2·1=2; 21:7=3 и т.п. Затем начинают встречаться равенства, в записи которых участвуют числовые выражения разного рода. Например, (2+2)+5=2+(5+2); 4·(4−(1+2))+12:4−1=4·1+3−1 и т.п. Дальше мы знакомимся с прочими видами чисел, и числовые равенства приобретают все более и более интересный и разнообразный вид.
Определение 1
Числовое равенство – это равенство, обе части которого состоят из чисел и/или числовых выражений.
Свойства числовых равенств
Сложно переоценить значимость свойств числовых равенств в математике: они являются опорой многому, определяют принцип работы с числовыми равенствами, методы решений, правила работы с формулами и многое другое.Очевидно, что существует необходимость детального изучения свойств числовых равенств.
Свойства числовых равенств абсолютно согласованы с тем, как определяются действия с числами, а также с определением равных чисел через разность: число a равно числу bтолько в тех случаях, когда разность a−b есть нуль. Далее в описании каждого свойства мы проследим эту связь.
Основные свойства числовых равенств
Изучать свойства числовых равенств начнем с трех базовых свойств, которые присущи всем равенствам. Перечислим основные свойства числовых равенств:
- свойство рефлексивности: a=a;
- свойство симметричности: если a=b, то b=a;
- свойство транзитивности: если a=b и b=c, то a=c,где a, b и c – произвольные числа.
Определение 2
Свойство рефлексивности обозначает факт равенства числа самому себе: к примеру, 6=6, −3=−3, 437=437 и т.п.
Доказательство 1
Нетрудно продемонстрировать справедливость равенства a−a=0для любого числа a: разность a−a можно записать как сумму a+(−a), а свойство сложения чисел дает нам возможность утверждать, что любому числу a соответствует единственное противоположное число −a, и сумма их есть нуль.
Определение 3
Согласно свойству симметричности числовых равенств: если число a равно числу b,
то число b равно числу a. К примеру, 43=64, тогда 64=43.
Доказательство 2
Обосновать данное свойство можно через разность чисел. Условию a=b соответствует равенство a−b=0. Докажем, что b−a=0.
Запишем разность b−aв виде −(a−b), опираясь на правило раскрытия скобок, перед которыми стоит знак минус. Новая запись выражения равна -0, а число, противоположное нулю, это нуль. Таким образом, b−a=0, следовательно: b=a.
Определение 4
Свойство транзитивности числовых равенств гласит, что два числа равны друг другу в случае их одновременного равенства третьему числу. К примеру, если 81=9 и 9=32, то 81=32.
Свойству транзитивности также отвечает определение равных чисел через разность и свойства действий с числами. Равенствам a=b и b=c соответствуют равенства a−b=0 и b−c=0.
Доказательство 3
Докажем справедливость равенства a−c=0, из чего последует равенство чисел a и c. Посколькусложение числа с нулем не меняет само число, то a−c запишем в виде a+0−c. Вместо нуля подставим сумму противоположных чисел −b и b, тогда крайнее выражение станет таким: a+(−b+b)−c. Выполним группировку слагаемых: (a−b)+(b−c). Разности в скобках равны нулю, тогда и сумма (a−b)+(b−c) есть нуль. Это доказывает, что, когда a−b=0 и b−c=0, верно равенство a−c=0, откуда a=c.
Прочие важные свойства числовых равенств
Основные свойства числовых равенств, рассмотренные выше, являются базисом для ряда дополнительных свойств, довольно ценных в разрезе практики. Перечислим их:
Определение 5
Прибавив к (или убавив от) обеим частям числового равенства, являющегося верным, одно и то же число, получим верное числовое равенство. Запишем буквенно: если a=b, где a и b – некоторые числа, то a+c=b+c при любом c.
Доказательство 4
В качестве обоснования запишем разность (a+c)−(b+c).
Это выражение легко преобразуется в вид (a−b)+(c−c).
Из a=b по условию следует, что a−b=0 и c−c=0, тогда (a−b)+(c−c)=0+0=0. Это доказывает, что (a+c)−(b+c)=0, следовательно, a+c=b+c;
Определение 6
Если обе части верного числового равенства перемножить с любым числом или разделить на число, не равное нулю, тогда получим верное числовое равенство.
Запишем буквенно: когда a=b, то a·c=b·c при любом числе c. Если c≠0, тогда и a:c=b:c.
Доказательство 5
Равенство верно: a·c−b·c=(a−b)·c=0·c=0, и из него следует равенство произведений a·c и b·c. А деление на отличное от нуля число c возможно записать как умножение на обратное число 1c;
Определение 7
При a и b, отличных от нуля и равных между собой, обратные им числа также равны.
Запишем: когда a≠0, b≠0 и a=b, то 1a=1b. Крайнее равенство нетрудно доказать: с этой целью разделим обе части равенства a=b на число, равное произведению a·b и не равное нулю.
Укажем еще на пару свойств, которые позволяют осуществлять сложение и умножение соответствующих частей верных числовых равенств:
Определение 8
При почленном сложении верных числовых равенств получается верное равенство. Запись этого свойства такова: если a=b и c=d, то a+c=b+d для любых чисел a, b, c и d.
Доказательство 6
Обосновать это полезное свойство возможно, опираясь на указанные ранее свойства. Мы знаем, что к обеим частям верного равенства возможно прибавить любое число.
К равенству a=bприбавим число c, а к равенству c=d — число b, итогом станут верные числовые равенства: a+c=b+c и c+b=d+b. Крайнее запишем в виде: b+c=b+d. Из равенств a+c=b+c и b+c=b+d согласно свойству транзитивности следует равенство a+c=b+d. Что и нужно было доказать.
Необходимо уточнить, что почленно можно сложить не только два верных числовых равенства, но и три, и более;
Определение 7
Наконец, опишем такое свойство: почленное перемножение двух верных числовых равенств дает верное равенство. Запишем при помощи букв: если a=b и c=d, то a·c=b·d.
Доказательство 7
Доказательство этого свойства подобно доказательству предыдущего. Умножим обе части равенства на любое число, умножим a=b на c, а c=d на b, получим верные числовые равенства a·c=b·c и c·b=d·b. Крайнее запишем как b·c=b·d. Свойство транзитивности дает возможность из равенства a·c=b·c и b·c=b·d вывести равенство a·c=b·d, которое нам необходимо было доказать.
И вновь уточним, что данное свойство применимо для двух, трех и более числовых равенств.
Так, можно записать: если a=b, то an=bn для любых чисел a и b, и любого натурального числа n.
Завершим данную статью, собрав для наглядности все рассмотренные свойства:
a=a.
Если a=b, то b=a.
Если a=bи b=c, то a=c.
Если a=b, то a+c=b+c.
Если a=b, то a·c=b·c.
Если a=bи с≠0, то a:c=b:c.
Если a=b, a=b, a≠0 и b≠0, то 1a=1b.
Если a=b и c=d, то a·c=b·d.
Если a=b, то an=bn.
50. Свойства равенств, на которых основывается решение уравнений. Возьмем какое-нибудь уравнение, не очень сложное, например:
7x – 24 = 15 – 3x
или
x/2 – (x – 3)/3 – (x – 5)/6 = 1
Мы видим в каждом уравнении знак равенства: все то, что написано слева от знака равенства, называется левою или первою частью уравнения (в первом уравнении 7x – 24 является левою или первою частью, а во втором x/2 – (x – 3)/3 – (x – 5)/6 есть первая, или левая, часть); все то, что написано справа от знака равенства, называется правою или второю частью уравнения (15 – 3x есть правая часть первого уравнения, 1 является правою, или вторю, частью 2-го уравнения).
Каждая часть любого уравнения выражает собою некоторое число. Числа, выражаемые левою и правою частью уравнения, должны быть равны между собою. Нам ясно: если мы к каждому из этих чисел прибавим по одинаковому числу, либо вычтем из них по одинаковому числу, либо каждое из них умножим на одинаковое число, либо, наконец, разделим на одно и то же число, то результаты этих действий должны также быть равными между собою. Другими словами: если a = b, то a + c = b + c, a – c = b – c, ac = bc и a/c = b/c. По поводу деления следует, однако, иметь в виду, что в арифметике не имеется деления на нуль — мы не умеем, например, число 5 разделить на нуль. Поэтому в равенстве a/c = b/c число c не может быть равным нулю.
Итак:
- К обеим частям уравнения можно прибавить или из них вычесть по одинаковому числу.
- Обе части уравнения можно умножить или разделить на одно и то же число, исключая случай, когда это число может оказаться равным нулю.
Пользуясь этими свойствами уравнения, мы можем найти удобный способ решать уравнения. Выясним этот случай на примерах.
Пример 1. Пусть надо решить уравнение
5x – 7 = 4x + 15.
Мы видим, что первая часть уравнения содержит два члена; один из них 5x, содержащий неизвестный множитель x, можно назвать неизвестным членом, а другой –7 – известным. Во второй части уравнения также 2 члена: неизвестный 4x и известный +15. Сделаем так, чтобы в левой части уравнения оказались только неизвестные члены (а известный член –7 уничтожился бы), а в правой части оказались бы только известные члены (а неизвестный член +4x уничтожился бы). Для этой цели прибавим к обеим частям уравнения одинаковые числа: 1) прибавим по +7 (чтобы уничтожился член –7) и 2) прибавим по –4x (чтобы уничтожился член +4x). Тогда получим:
5x – 7 + 7 – 4x = 4x + 15 + 7 – 4x
Сделав в каждой части уравнения приведение подобных членов, получим
x = 22.
Это равенство и является решением уравнения, так как оно указывает, что для x надо взять число 22.
Пример 2. Решить уравнение:
8x + 11 = 7 – 4x
Опять прибавим к обеим частям уравнения по –11 и по +4x, получим:
8x + 11 – 11 + 4x = 7 – 4x – 11 + 4x
Выполнив приведение подобных членов, получим:
12x = –4
Разделим теперь обе части уравнения на +12, получим:
x = –4/12 или x = –1/3
(первую часть уравнения 12x разделить на 12 – получим 12x/12 или просто x; вторую часть уравнения –4 разделить на +12 – получим –4/12 или –1/3).
Последнее равенство и является решением уравнения, так как оно указывает, что для x надо взять число –1/3.
Пример 3. Решить уравнением
x – 23 = 3 · (2x – 3)
Раскроем сначала скобки, получим:
x – 23 = 6x – 9
Прибавим к обеим частям уравнения по +23 и по –6x, – получим:
x – 23 + 23 – 6x = 6x – 9 + 23 – 6x.
Теперь, для того, чтобы впоследствии ускорить процесс решения уравнения, не будем сразу выполнять приведение всех подобных членов, а только заметим, что члены –23 и +23 в левой части уравнения взаимно уничтожаются, также члены +6x и –6x в первой части взаимно уничтожаются – получим:
x – 6x = –9 + 23.
Сравним это уравнение с начальным: вначале было уравнение:
x – 23 = 6x – 9
Теперь получили уравнение:
x – 6x = –9 + 23.
Мы видим, что в конце концов оказалось, что член –23, находившийся сначала в левой части уравнения, теперь как бы перешел в правую часть уравнения, причем у него переменился знак (в левой части начального уравнения был член –23, теперь его там нет, но зато в правой части уравнения имеется член + 23, которого там раньше не было). Так же точно в правой части уравнения был член +6x, теперь его там нет, но появился зато в левой части уравнения член –6x, которого раньше там не было. Рассматривая с этой точки зрения примеры 1 и 2, мы придем к общему заключению:
Можно любой член уравнения перенести из одной части в другую, меняя знак у этого члена (в дальнейших примерах мы будем этим пользоваться).
Итак, возвращаясь к нашему примеру, мы получили уравнение
x – 6x = –9 + 23
Выполним приведение подобных членов:
–5x = +14
Разделим обе части уравнения на –5. Тогда получим:
x = –2(4/5)
[–5x : (–5) получим x] – это и есть решение нашего уравнения.
Пример 4. Решить уравнение:
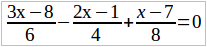
Сделаем так, чтобы в уравнении не было дробей. Для этой цели найдем общего знаменателя для наших дробей – общим знаменателем служит число 24 – и умножим на него обе части нашего уравнения (можно, ведь, чтобы равенство не нарушалось, умножить на одно и то же число только обе части уравнения). В первой части 3 члена, причем каждый член является дробью — надо, следовательно, каждую дробь умножить на 24: вторая часть уравнения есть 0, а нуль умножить на 24 — получим нуль. Итак,
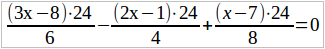
Мы видим, что каждая из наших трех дробей, благодаря тому, что она умножена на общее наименьшее кратное знаменателей этих дробей, сократится и сделается целым выражением, а именно получим:
(3x – 8) · 4 – (2x – 1) · 6 + (x – 7) · 3 = 0
Конечно, желательно все это выполнить в уме: надо вообразить, что, например, числитель первой дроби заключается в скобки и умножается на 24, после чего воображение поможет нам увидеть сокращение это дроби (на 6) и конечный результат, т. е. (3x – 8) · 4. Тоже имеет место и для остальных дробей. Раскроем теперь в полученном уравнении (в его левой части) скобки:
12x – 32 – 12x + 6 + 3x – 21 = 0
(обратим внимание, что здесь понадобилось двучлен 2x – 1 умножить на 6 и полученное произведение 12x – 6 вычесть из предыдущего, благодаря чему знаки членов этого произведения должны перемениться — выше и написано –12x + 6). Перенесем известные члены (т. е. –32, +6 и –21) из левой части уравнения в его правую часть, причем (как мы уже знаем) знаки этих членов должны перемениться — получим:
12x – 12x + 3x = 32 – 6 + 21.
Выполним приведение подобных членов:
3x = 47
(при навыке должно сразу выполняться и перенесение нужных членов из одной части уравнения в другую и приведение подобных членов), разделим, наконец, обе части уравнения на 3 — получим:
x = 15(2/3) — это и есть решение уравнения.
Пример 5. Решить уравнение:
5 – (3x + 1)/7 = x + (2x – 3)/5
Здесь две дроби, и их общий знаменатель равен 35. Умножим, чтобы освободить уравнение от дробей, обе части уравнения на общего знаменателя 35. В каждой части нашего уравнения 2 члена. При умножении каждой части на 35 должно каждый член умножить на 35 — получим:
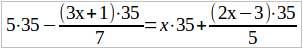
Дроби сократятся — получим:
175 – (3x + 1) · 5 = 35x + (2x – 3) · 7
(конечно, можно было бы при навыке написать сразу это уравнение).
Выполним все действия:
175 – 15x – 5 = 35x + 14x – 21.
Перенесем все неизвестные члены из правой части (т. е. члены +35x и +14x) в левую, а все известные члены из левой части (т. е. члены +175 и –5) в правую — следует при этом не забывать у переносимых членов менять знак:
–15x – 35x – 14x = –21 – 175 + 5
(член –15x, как раньше был в левой части, так и теперь в ней остался — у него поэтому отнюдь не следует менять знака; аналогичное имеет место и для члена –21). Сделав приведение подобных членов, получим:
–64x = –191.
[Возможно сделать так, чтобы не было знака минус в обеих частях уравнения; для этого умножим обе части уравнения на (–1), получим 64x = 191, но этого можно и не делать.]
Разделим затем обе части уравнения на (–64), получим решение нашего уравнения
x = 2(63/64)
[Если умножили обе части уравнения на (–1) и получили уравнение 64x = 191, то теперь надо обе части уравнения разделить на 64.]
На основании того, что пришлось выполнять в примерах 4 и 5, мы можем установить: можно освободить уравнение от дробей — для этого надо найти общего знаменателя для всех дробей, входящих в уравнение (или наименьшее общее кратное знаменателей всех дробей) и на него умножить обе части уравнения — тогда дроби должны исчезнуть.
Пример 6. Решить уравнение:
5x = 4x.
Перенеся член 4x из правой части уравнения в левую, получим:
5x – 4x = 0 или x = 0.
Итак, решение найдено: для x надо взять число нуль. Если мы заменим в данном уравнении x нулем, получим 5 · 0 = 4 · 0 или 0 = 0, что указывает на выполнение требования, выражаемого данным уравнением: найти такое число для x, чтобы одночлен 5x оказался равен тому же самому числу, как и одночлен 4x.
Если кто-либо подметит с самого начала, что обе части уравнения 5x = 4x можно разделить на x и выполнит это деление, то получится явная несообразность 5 = 4! Причиною этого является то обстоятельство, что деление 5x/x в данном случае выполнить нельзя, так как, мы видели выше, вопрос, выражаемый нашим уравнением, требует, чтобы x = 0, а деление на нуль не выполнимо.
Заметим еще, что и умножение на нуль требует некоторой внимательности: умножая на нуль и два неравных числа, мы получим в результате этих умножений равные произведения, а именно — нули.
Если, например, мы имеем уравнение
x – 3 = 7 – x (его решение: x = 5)
и если кто-либо захочет к нему применить свойство «обе части уравнения можно умножить на одно и тоже число» и умножить обе части на x, то получит:
x2 – 3x = 7x – x2.
После этого может обратить на себя внимание, что все члены уравнения содержат множителя x, из чего можно сделать заключение, что для решения этого уравнения можно взять число нуль, т. е. положить x = 0. И в самом деле, тогда получим:
02 – 3 · 0 = 7 · 0 – 02 или 0 = 0.
Однако, это решение x = 0, очевидно, не годится для данного уравнения x – 3 = 7 – x; заменяя в нем x нулем, получим явную несообразность: 3 = 7!
Числовые равенства и неравенства. Методика изучения числовых равенств и неравенств.
Возьмём два числовых выражения 32-20 и 144 : 12.
Соединим их знаком равенства. 32 -20 = 144 : 12 (и), т. к. 12=12
Получим высказывание, которое называется числовым равенством.
Это высказывание истинно.
14 + 4 • 8 = 4 • 9 (л), т. к. 46≠ 36
Определение 1. Два числа или два числовых выражения, соединённые знаком равенства, называются числовым равенством.
Определение 2. Высказывание вида a = b , где а и в числовые выражения, называется числовым равенством.
Символически числовое равенство записывается так: a = b.
Если знаком равенства соединены 2 числовых выражения, значения которых равны, то получится истинное числовое равенство, если не равны, то ложное.
Таким образом, с логической точки зрения числовое равенство — это высказывание, истинное или ложное.
Числовое равенство истинно, если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают.
Свойства истинных числовых равенств
1) Если к обеим частям истинного числового равенства прибавить одно и то же число с, или числовое выражение, имеющее смысл, то получится истинное числовое равенство.
Если a = b (и), то a +c = b + c тоже истинно.
Дано: a = b истинное числовое равенство, c – число или числовое выражение, имеющее смысл
Доказать: a +c = b + c (и).
Доказательство:
По свойству рефлексивности отношения «равно» можно записать a +c = a + c .
По условию a = b , в правой части равенства заменим а на в, получим, а + с = в + с ч.т.д.
Следствие: Любой член истинного числового равенства можно переносить из одной части в другую, поменяв знак на противоположный.
a + m = b + m + n
a = — m + b + m + n
a = b + n
2) Если обе части истинного числового равенства умножить на одно и то же число с, или числовое выражение, имеющее смысл, то получится истинное числовое равенство.
Если a = b (и), то a• c = b•c тоже истинно.
Дано: a = b истинное числовое равенство, c – число или числовое выражение, имеющее смысл
Доказать: a•c = b• c (и).
Доказательство:
По свойству рефлексивности отношения «равно» можно записать a• c = a•c .
По условию a = b , в правой части равенства заменим а на в, получим, а • с = в • с ч.т.д.
Следствие: Обе части истинного числового равенства можно разделить на одно и то же число, не равное нулю.
В начальной школе истинные числовые равенства называют верными, ложные– неверными.
II. Повторение.
-Какие выражения называются числовыми выражениями? (Они образуются из чисел, знаков действий и скобок).
-Что такое значение числового выражения? (Если выполнить все действия, указанные в выражении, получим число, которое называется значением числового выражения).
-Существуют ли числовые выражения, значения которых нельзя найти?
Какие действия выполняются раньше 1 или 2 ступени? (действия второй ступени (умножение и деление), а затем действия первой ступени (сложение и вычитание)).
-Что называетсявыражением с переменной (Запись, состоящая из чисел, знаков действий, скобок и букв)
-Областью определения выражения с переменной? (множество тех значений переменной, при которых выражение имеет смысл).
-Какие преобразования относятся к тождественным?
-приведение подобных;
-раскрытие скобок;
-приведение дробей к общему знаменателю;
-группировка или заключение в скобки)
-Что такое тождественное преобразование? (Замена выражения с переменной другим выражением тождественно равным ему называется тождественным преобразованием).
-Как называются такие записи: (3 + 2)) — 12 или 3х-у:+)8, (их нельзя назвать ни числовым выражением, ни выражением с переменной).
Задача 1. Найти значение выражения Зх(х-2) + 4(х-2) при х = 6.
Решение.
1 способ. Подставим число 6 вместо переменной в данное выражение: 3-6(6-2) + 4(6-2). Чтобы найти значение полученного числового выражения, выполним все указанные действия:
3-6-(6-2) + 4-(6-2) = 18-4 + 4-4 = 72+ 16 = 88. Следовательно, при х = 6 значение выражения
Зх(х-2)+4(х-2) равно 88.
2 способ. Прежде чем подставлять число 6 в данное выражение, упростим его:
Зх(х-2) + 4(х-2) = (х-2)(Зх+4). И затем, подставив в полученное выражение вместо Х число 6, выполним действия: (6-2)-(3-6 + 4)= 4-(18+4) = 4-22 = 88.
Обратим внимание на следующее: и при первом способе решения задачи, и при втором мы одно выражение заменяли другим. Например, выражение 18-4+4-4 заменяли выражением 72+16, а выражение Зх (х-2) + 4(х-2)-выражением (х — 2)(3х + 4), причем эти замены привели к одному и тому же результату. В математике, описывая решение данной задачи, говорят, что мы выполняли тождественные преобразования выражений.
-Какие два выражения называются тождественно равными? (если при любых значениях переменных из области определения выражений их соответственные значения равны).
— Как получить тождество? (Если два тождественно равных на некотором множестве выражения соединить знаком равенства, то получим предложение, которое называют тождествомна этом множестве).
Например, 5(х + 2) = 5х + 10 — тождество на множестве действительных чисел, потому что для всех действительных чисел значения выражения 5(х + 2) и 5х + 10 совпадают. Используя обозначение квантора общности, это тождество можно записать так: ( х R)5(х + 2) = 5х + 10. Тождествами считают и верные числовые равенства.
Замена выражения другим, тождественно равным ему на некотором множестве, называется тождественным преобразованием данного выражения на этом множестве.
Задача 2. Разложить на множители выражение ax—bx+ab—b2.
Решение. Сгруппируем члены данного выражения по два (первый со вторым, третий с четвертым): ax—bx+ab—b2 = = (ax—bx) + (ab—b2). Это преобразование возможно на основании свойства ассоциативности сложения действительных чисел.
Вынесем в полученном выражении из каждой скобки общий множитель: (ax—bx)+(ab—b2) = x(a—b)+b(a—b) — это преобразование возможно на основании свойства дистрибутивности умножения относительно вычитания действительных чисел.
В полученном выражении слагаемые имеют общий множитель, вынесем его за скобки: x(a—b)+b(a—b) = (a—b)(x—b). Основой выполненного преобразования является свойство дистрибутивности умножения относительно сложения.
Итак, ax—bx+ab—b2 — (a—b)(x—b).
Числовые неравенства.
I. Повторение изученного:
— Какое предложение называют числовым равенством?
— Приведите примеры числовых равенств.
Возьмем, например, числовые выражения 3 + 2 и 6 — 1 и соединим их знаком равенства 3 + 2 = 6-1. Оно истинное. Если же соединить знаком равенства 3 + 2 и 7 — 3, то получим ложное числовое равенство 3 + 2 = 7-3.
— Можно ли числовое равенство считать высказыванием? (Да)
— Какое числовое равенство истинно? (Если значения числовых выражений, стоящих в левой и правой частях равенства, совпадают).
— Назовите свойства истинных числовых равенств.
Если к обеим частям истинного числового равенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое равенство.
Если обе части истинного числового равенства умножить на одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое равенство.
Если два числовых выражения соединить знаком «>» или «<», то получим числовое неравенство.
Определение. Два числовых выражения, соединённые знаком «>» или «<», образуют числовое неравенство.
Например, если соединить выражение 6 + 2 и 13-7 знаком «>», то получим истинное числовое неравенство 6 + 2 > 13-7 (И). Если соединить те же выражения знаком «<», получим ложное числовое неравенство 6 +2 < 13-7(Л).
Таким образом, с логической точки зрения числовое неравенство — это высказывание, истинное или ложное. А, следовательно, к числовым неравенствам можно применить логические операции.
Конъюнкцию двух числовых неравенств принято записывать в виде двойного неравенства.
(5 > 4 / 5 < 6) <=> (4 < 5 < 6)
Дизъюнкцию числового равенства и неравенства записывают в виде нестрогого неравенства
(5 > 4 V 5 = 4) <=> (5≥ 4 )
Определение. Если два числовых неравенства имеют одинаковые знаки, то их называют неравенствами одинакового смысла, если у неравенств разные знаки, то неравенствами противоположного смысла.
a >b и c > d – одинакового смысла;
a >b и c < d – противоположного смысла.
Рассмотрим свойства истинных числовых неравенств.
Свойство 1.
Для любых чисел a и b верно, что если a >b, то a — b > 0.
(a, b) (a >b=>a — b > 0).
Доказательство:
Нам дано, что a >b.По опр отношения «>», существует такое натуральное число к, что a = b + к. => по 2 опр разности a — b = к. Так как к N , к > 0, то a — b > 0 ч.т.д.
Свойство 2.
Если к обеим частям истинного числового неравенства прибавить одно и то же числовое выражение, имеющее смысл, то получим также истинное числовое неравенство.
(a, b, с) (a >b => a +с > b + с).
Доказательство:
По условию a > b, тогда по 1 свойству a — b > 0 => (a — b) + (с – с) > 0 =>применяем сочет свойство (a + с) — (b + с) > 0 => по свойству 1 a +с > b + с ч.т.д.
Свойство 3.
Обе части истинного числового неравенства можно умножать на одно и то же положительное число, в результате получим истинное числовое неравенство того же смысла.
(a, b, с>0) (a >b => a • с > b • с).
Доказательство:
По условию a > b, => a — b > 0 => (a — b) • с > 0 =>применяем распределит свойство a • с — b • с > 0 => a • с > b • с ч.т.д.
Свойство 4.
Обе части истинного числового неравенства можно умножать на одно и то же отрицательное число, в результате получим истинное числовое неравенство противоположного смысла (с противоположным знаком).
(a, b, с<0) (a >b => a • с < b • с).
Свойство 5
Истинные числовые неравенства одинакового смысла можно почленно складывать, в результате получается неравенство того же смысла.
(a, b, с, d) (a >b и c >d => a + c > b +d).
Свойство 6
Истинные числовые неравенства противоположного смысла можно почленно вычитать, сохраняя знак того неравенства, из которого вычитаем.
(a, b, с, d) (a > b и c => a — c > b — d).
Свойство 7
Истинные числовые неравенства одинакового смысла с положительными частями можно почленно перемножать, в результате получается истинное числовое неравенство того же смысла.
(a, b, с, d) (a >b >0 и c >d >0 => a • c > b • d).
Свойство 8
Истинные числовые неравенства одинакового смысла с отрицательными частями можно почленно перемножать, в результате получается истинное числовое неравенство противоположного смысла.
(a, b, с, d) (a < b < 0 и c < d < 0 => a • c > b • d).
Свойство 9
Обе части истинного числового неравенства можно возводить в одну и ту же степень с натуральным показателем, при этом получается неравенство того же смысла.
(a, b и nN) (a > b =>an > bn).
