Умножение произведения на число это какое свойство умножения

- Переместительное свойство умножения
- Сочетательное свойство умножения
- Распределительное свойство умножения
Переместительное свойство умножения
От перестановки сомножителей местами произведение не меняется.
Следовательно, для любых чисел a и b верно равенство:
a · b = b · a
выражающее переместительное свойство умножения.
Примеры:
6 · 7 = 7 · 6 = 42
4 · 2 · 3 = 3 · 2 · 4 = 24
Обратите внимание, что данное свойство можно применять и к произведениям, в которых более двух множителей.
Сочетательное свойство умножения
Результат умножения трёх и более множителей не изменится, если какую-либо группу множителей заменить их произведением.
Следовательно, для любых чисел a, b и c верно равенство:
a · b · c = (a · b) · c = a · (b · c)
выражающее сочетательное свойство умножения.
Пример:
3 · 2 · 5 = 3 · (2 · 5) = 3 · 10 = 30
или
3 · 2 · 5 = (3 · 2) · 5 = 6 · 5 = 30
Сочетательное свойство используется для удобства и упрощения вычислений при умножении. Например:
25 · 15 · 4 = (25 · 4) · 15 = 100 · 15 = 1500
В данном случае можно было вычислить всё последовательно:
25 · 15 · 4 = (25 · 15) · 4 = 375 · 4 = 1500
но проще и легче сначала умножить 25 на 4 и получить 100, а уже потом умножить 100 на 15.
Распределительное свойство умножения
Сначала рассмотрим распределительное свойство умножения относительно сложения:
Чтобы число умножить на сумму чисел, можно это число умножить отдельно на каждое слагаемое и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a + b) = m · a + m · b
выражающее распределительное свойство умножения.
Так как в данном случае число и сумма являются множителями, то, поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы сумму чисел умножить на число, можно каждое слагаемое отдельно умножить на это число и полученные произведения сложить.
Следовательно, для любых чисел a, b и m верно равенство:
(a + b) · m = a · m + b · m
Теперь рассмотрим распределительное свойство умножения относительно вычитания:
Чтобы число умножить на разность чисел, можно это число умножить отдельно на уменьшаемое и вычитаемое и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
m · (a — b) = m · a — m · b
Так как в данном случае число и разность являются множителями, то поменяв их местами, используя переместительное свойство, можно сформулировать распределительное свойство так:
Чтобы разность чисел умножить на число, можно уменьшаемое и вычитаемое отдельно умножить на это число и из первого полученного произведения вычесть второе.
Следовательно, для любых чисел a, b и m верно равенство:
(a — b) · m = a · m — b · m
Переход от умножения:
m · (a + b) и m · (a — b)
соответственно к сложению и вычитанию:
m · a + m · b и m · a — m · b
называется раскрытием скобок.
Переход от сложения и вычитания:
m · a + m · b и m · a — m · b
к умножению:
m · (a + b) и m · (a — b)
называется вынесением общего множителя за скобки.
Для операции умножения натуральных чисел ℕ характерен ряд результатов, которые справедливы для любых умножаемых натуральных чисел. Эти результаты называются свойствами. В данной статье мы сформулируем свойства умножения натуральных чисел, приведем их буквенные определения и примеры.
Переместительное свойство умножения натуральных чисел
Переместительное свойство часто называют также переместительным законом умножения. По аналогии с переместительным свойством для сложения чисел, оно формулируется так:
Переместительный закон умножения
От перемены мест множителей произведение не меняется.
В буквенном виде переместительное свойство записывается так: a·b=b·a
a и b — любые натуральные числа.
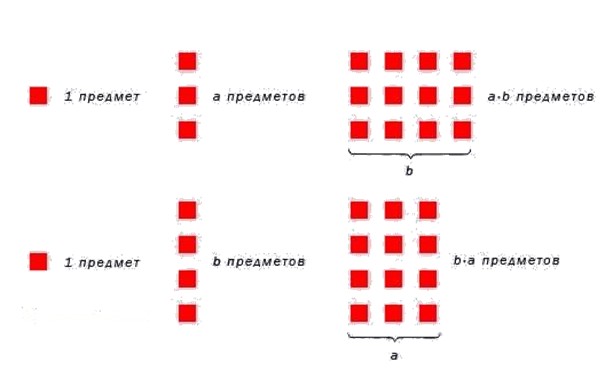
Возьмем любые два натурльных числа и наглядно покажем, что данное свойство справедливо. Вычислим произведение 2·6. По определению произведения, нужно число 2 повторить 6 раз. Получаем: 2·6=2+2+2+2+2+2=12. Теперь поменяем множители местами. 6·2=6+6=12. Очевидно, переместительный закон выполняется.
На рисунке ниже проиллюститруем переместительное свойство умножения натуральных чисел.
Сочетательное свойство умножения натуральных чисел
Второе название для сочетательного свойства умножения — ассоциативный закон, или ассоциативное свойство. Вот его формулировка.
Сочетательный закон умножения
Умножение числа a на произведение чисел b и c равносильно умножению произведения чисел a и b на число c.
Приведем формулировку в буквенном виде:
a·b·c=a·b·c
a, b, c — любые натуральные числа. Сочетательный закон работает для трех и более натуральных чисел.
Для наглядности приведем пример. Сначала вычислим значение 4·3·2.
4·3·2=4·6=4+4+4+4+4+4=24
Теперь переставим скобки и вычислим значение 4·3·2.
4·3·2=12·2=12+12=24
4·3·2=4·3·2
Как видим, теория совпадает с практикой, и свойство справедливо.
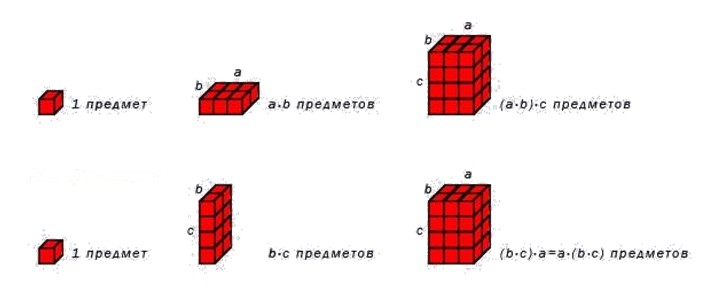
Сочетательное свойство умножения также можно проиллюстрировать с помощью рисунка.
Распределительное свойство относительно умножения
Без распределительного свойста не обойтись, когда в математическом выражении одновременно присутствуют операции умножения и сложения. Это свойство определяет связь между умножением и сложением натуральных чисел.
Распределительное свойство умножения относительно сложения
Умножения суммы чисел b и c на число a равносильно сумме произведений чисел a и b и a и c.
Запишем в форме буквенного выражения:
a·b+c=a·b+a·c
a, b, c — любые натуральные числа.
Теперь на наглядном примере покажем, как работает это свойство. Вычислим значение выражения 4·3+2.
4·3+2=4·3+4·2=12+8=20
С другой стороны 4·3+2=4·5=20. Справедливость распределительного свойства умножения относительно сложения показана наглядно.
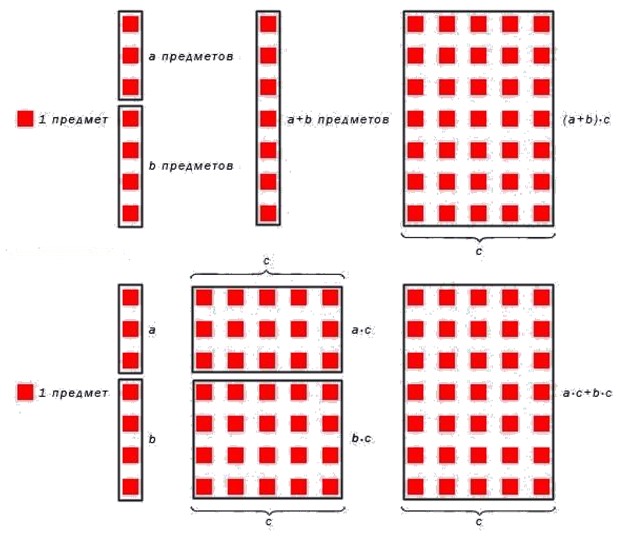
Для лучшего понимания приведем рисунок, иллюстрирующий суть умножения числа на сумму чисел.
Распределительное свойство умножения относительно вычитания
Распределительное свойство умножения относительно вычитания формулируется аналогично данному свойству относительно сложения, следует лишь учитывать знак операции.
Распределительное свойство умножения относительно вычитания
Умножения разности чисел b и c на число a равносильно разности произведений чисел a и b и a и c.
Запишем в форме буквенного выражения:
a·b-c=a·b-a·c
a, b, c — любые натуральные числа.
В предыдущем примере заменим «плюс» на «минус» и запишем:
4·3-2=4·3-4·2=12-8=4
С другой стороны 4·3-2=4·1=4. Таким образом, справедливость свойства умножения натуральных чисел относительно вычитания показана наглядно.
Умножение единицы на натуральное число
Умножение единицы на натуральное число
Умножение единицы на любое натуральное число в результате дает данное число.
1·a=a
По определению операции умножения, произведение чисел 1 и a равно сумме, в котором слагаемое 1 повторяется a раз.
1·a=∑i=1a1
Умножение натурального числа a на единицу представляет собой сумму, состоящую из одого слагаемого a. Таким образом, переместительное свойство умножения остается справедливым:
1·a=a·1=a
Умножение нуля на натуральное число
Число 0 не входит в множество натуральных чисел. Тем не менее, есть смысл рассмотреть свойство умножения нуля на натуральное число. Данное свойство часто используется при умножении натуральных чисел столбиком.
Умножение нуля на натуральное число
Произведение числа 0 и любого натурального числа a равно числу 0.
0·a=0.
По определению, произведение 0·a равно сумме, в которой слагаемое 0 повторяется a раз. По свойствам сложения, такая сумма равна нулю.
В результате умножения единицы на нуль получается нуль. Произведение нуля на сколь угодно большое натуральное число также дает в результате нуль.
Напимер: 0·498=0; 0·9638854785885=0
Справедливо и обратное. Произведение числа на нуль также дает в результате нуль: a·0=0.
Óìíîæåíèå — îäíî èç ÷åòûð¸õ îñíîâíûõ àðèôìåòè÷åñêèõ äåéñòâèé, áèíàðíàÿ ìàòåìàòè÷åñêàÿ îïåðàöèÿ, â êîòîðîé îäèí àðãóìåíò ñêëàäûâàåòñÿ ñòîëüêî ðàç, ñêîëüêî ïîêàçûâàåò äðóãîé.
Ïðîèçâåäåíèå ÷èñåë m è n — ýòî ñóììà n ñëàãàåìûõ, êàæäîå èç ýòèõ ñëàãàåìûõ = m.
Âûðàæåíèå òèïà m • n, è çíà÷åíèå òàêîãî âûðàæåíèÿ íàçûâàåòñÿ ïðîèçâåäåíèå ÷èñåë m è n. ×èñëà m è n íàçûâàþòñÿ ìíîæèòåëÿìè.
Åñëè óñòíîå óìíîæåíèå ÷èñåë çàòðóäíèòåëüíî èñïîëüçóþò óìíîæåíèå â ñòîëáèê.  ñòîëáèê ìîæíî óìíîæàòü áîëüøèå íàòóðàëüíûå ÷èñëà èëè äåñÿòè÷íûå äðîáè.
Ñâîéñòâà óìíîæåíèÿ ÷èñåë.
1. Êîììóòàòèâíîñòü: 
Ïðè ïåðåñòàíîâêå ìíîæèòåëåé ìåñòàìè, çíà÷åíèå ïðîèçâåäåíèÿ îñòàåòñÿ áåç èçìåíåíèé. Ýòî ïåðåìåñòèòåëüíîå ñâîéñòâî óìíîæåíèÿ.
3 • 4 = 4 • 3 = 12 .
ãäå, 3 è 4 — ìíîæèòåëè, à 12 — ïðîèçâåäåíèå.
2. Àññîöèàòèâíîñòü: 
 ïðîèçâåäåíèè 3-õ è áîëüøå ìíîæèòåëåé ïðè ïåðåñòàíîâêå ýòèõ ìíîæèòåëåé ëèáî èçìåíåíèÿ ïîñëåäîâàòåëüíîñòè âûïîëíåíèÿ óìíîæåíèÿ ðåçóëüòàò îñòàåòñÿ îäèíàêîâûì.
Ïðèìåð:
(6 • 2) • 3 = 12 • 3 = 36 èëè 6 • (2 • 3) = 6 • 6 = 36 .
3. Äèñòðèáóòèâíîñòü: 
4. Ïðîèçâåäåíèå âñÿêîãî íàòóðàëüíîãî ÷èñëà è åäèíèöû, áóäåò ñîîòâåòñòâîâàòü ýòîìó ÷èñëó.
n • 1 = n.
Ïðîèçâåäåíèå âñÿêîãî íàòóðàëüíîãî ÷èñëà è íóëÿ, = 0.
n • 0 = 0.
Âûðàæåíèÿ ñ áóêâåííûìè ìíîæèòåëÿìè çàïèñûâàþò òàê:
âìåñòî 8 • x ïèøóò 8x , âìåñòî a • b ïèøóò ab.
Êðîìå òîãî, íå èñïîëüçóþò çíàê óìíîæåíèÿ è ïåðåä ñêîáêàìè,
2 • (a + b) çàïèñûâàþò êàê 2(à + b),
(x + 2) • (y + 3) çàïèñûâàþò êàê (x + 2)(y + 3),
a • (b • c) çàïèñûâàþò êàê abc.
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Äåéñòâèÿ ñ ÷èñëàìè. | |
| Äåéñòâèÿ ñ íàòóðàëüíûìè, ìíîãîçíà÷íûìè, êîìïëåêñíûìè ÷èñëàìè, àðèôìåòè÷åñêèå äåéñòâèÿ ñ ÷èñëàìè, ïðèìåðû äåéñòâèÿ ñ îòðèöàòåëüíûìè, íàòóðàëüíûìè ÷èñëàìè | |
| Äåéñòâèÿ ñ ÷èñëàìè. | |
×èñëà. | |
| Ïðîñòûå, íàòóðàëüíûå, äåéñòâèòåëüíûå, ðàöèîíàëüíûå, öåëûå, âåùåñòâåííûå ÷èñëà | |
| ×èñëà. | |
Ìàòåìàòèêà 4,5,6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ìàòåìàòèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ìàòåìàòèêà 4,5,6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
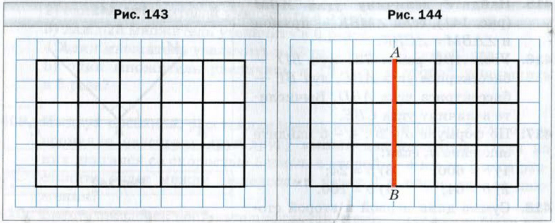
Начертим на листке в клетку прямоугольник со сторонами 5 см и 3 см. Разобьем его на квадраты со стороной 1 см (рис. 143). Подсчитаем количество клеток, расположенных в прямоугольнике. Это можно сделать, например, так.
Количество квадратов со стороной 1 см равно 5 * 3. Каждый такой квадрат состоит из четырех клеток. Поэтому общее число клеток равно (5 * 3) * 4.
Эту же задачу можно решить иначе. Каждый из пять столбцов прямоугольника состоит из трех квадратов со стороной 1 см. Поэтому в одном столбце содержится 3 * 4 клеток. Следовательно, всего клеток будет 5 * (3 * 4).
Подсчет клеток на рисунке 143 двумя способами иллюстрирует сочетательное свойство умножения для чисел 5, 3 и 4. Имеем: (5 * 3) * 4 = 5 * (3 * 4).
Чтобы произведение двух чисел умножить на третье число, можно первое число умножить на произведение второго и третьего чисел.
В буквенном виде это свойство записывают так:
(ab)c = a(bc)
Из переместительного и сочетательно свойств умножения следует, что при умножении нескольких чисел множители можно менять местами и заключать в скобки, тем самым определяя порядок вычислений.
Например, верны равенства:
abc = cba,
17 * 2 * 3 * 5 = (17 * 3) * (2 * 5).
На рисунке 144 отрезок AB делит рассмотренный выше прямоугольник на прямоугольник и квадрат.
Подсчитаем количество квадратов со стороной 1 см двумя способами.
С одной стороны, в образовавшемся квадрате их содержится 3 * 3, а в прямоугольнике − 3 * 2. Всего получим 3 * 3 + 3 * 2 квадратов. С другой стороны, в каждой из трех строчек данного прямоугольника находится 3 + 2 квадрата. Тогда их общее количество равно 3 * (3 + 2).
Равенсто 3 * (3 + 2) = 3 * 3 + 3 * 2 иллюстрирует распределительное свойство умножения относительно сложения.
Чтобы число умножить на сумму двух чисел, можно это число умножить на каждое слагаемое и полученные произведения сложить.
В буквенном виде это свойство записывают так:
a(b + c) = ab + ac
Из распределительного свойства умножения относительно сложения следует, что
ab + ac = a(b + c).
Это равенство позволяет формулу P = 2a + 2b для нахождения периметра прямоугольника записать в таком виде:
P = 2(a + b).
Заметим, что распределительное свойство справедливо для трех и более слагаемых. Например:
a(m + n + p + q) = am + an + ap + aq.
Также справедливо распределительное свойство умножения относительно вычитания: если b > c или b = c, то
a(b − c) = ab − ac
Пример 1. Вычислите удобным способом:
1) 25 * 867 * 4;
2) 329 * 75 + 329 * 246.
Решение.
1) Используем переместительное, а затме сочетательное свойства умножения:
25 * 867 * 4 = 867 * (25 * 4) = 867 * 100 = 86 700.
2) Имеем:
329 * 754 + 329 * 246 = 329 * (754 + 246) = 329 * 1 000 = 329 000.
Пример 2. Упростите выражение:
1) 4a * 3b;
2) 18m − 13m.
Решение.
1) Используя переместительное и сочетательное свойства умножения, получаем:
4a * 3b = (4 * 3) * ab = 12ab.
2) Используя распределительное свойство умножения относительно вычитания, получаем:
18m − 13m = m(18 − 13) = m * 5 = 5m.
Пример 3. Запишите выражение 5(2m + 7) так, чтобы оно не содержало скобок.
Решение.
Согласно распределительному свойству умножения относительно сложения имеем:
5(2m + 7) = 5 * 2m + 5 * 7 = 10m + 35.
Такое преобразование называют раскрытием скобок.
Пример 4. Вычислите удобным способом значение выражения 125 * 24 * 283.
Решение. Имеем:
125 * 24 * 283 = 125 * 8 * 3 * 283 = (125 * 8) * (3 * 283) = 1 000 * 849 = 849 000.
Пример 5. Выполните умножение: 3 сут 18 ч * 6.
Решение. Имеем:
3 сут 18 ч * 6 = 18 сут 108 ч = 22 сут 12 ч.
При решении примера было использовано распределительное свойство умножения относительно сложения:
3 сут 18 ч * 6 = (3 сут + 18 ч) * 6 = 3 сут * 6 + 18 ч * 6 = 18 сут + 108 ч = 18 сут + 96 ч + 12 ч = 18 сут + 4 сут + 12 ч = 22 сут 12 ч.
1. Переместительное свойство умножения натуральных чисел:
при перестановке множителей значение произведения не меняется.
Это переместительное свойство умножения. Если его записать буквами, то оно выглядит так:
m • n = n • m .
Рассмотрим пример, подтверждающий справедливость переместительного свойства умножения двух натуральных чисел. Отталкиваясь от смысла умножения двух натуральных чисел, вычислим произведение чисел 2 и 6, а также произведение чисел 6 и 2, и проверим равенство результатов умножения. Произведение чисел 6 и 2 равно сумме 6+6, из таблицы сложения находим 6+6=12. А произведение чисел 2 и 6 равно сумме 2+2+2+2+2+2, которая равна 12 (при необходимости смотрите материал статьи сложение трех и большего количества чисел). Следовательно, 6·2=2·6.
2. Сочетательное свойство умножения натуральных чисел:
умножить данное число на данное произведение двух чисел – это то же самое, что умножить данное число на первый множитель, и полученный результат умножить на второй множитель.
Сочетательное свойство умножения, a • (b • с) = (а • b) • c .
Приведем пример для подтверждения сочетательного свойства умножения натуральных чисел. Вычислим произведение 4·(3·2). По смыслу умножения имеем 3·2=3+3=6, тогда 4·(3·2)=4·6=4+4+4+4+4+4=24. А теперь выполним умножение (4·3)·2. Так как 4·3=4+4+4=12, то (4·3)·2=12·2=12+12=24. Таким образом, справедливо равенство 4·(3·2)=(4·3)·2, подтверждающее справедливость рассматриваемого свойства.
3. Распределительное свойство умножения относительно сложения:
умножить данную сумму двух чисел на данное число – это то же самое, что сложить произведение первого слагаемого и данного числа с произведением второго слагаемого и данного числа.
a·(b+c)=a·b+a·c.
Приведем пример, подтверждающий распределительное свойство умножения натуральных чисел. Проверим справедливость равенства (3+4)·2=3·2+4·2. Имеем (3+4)·2=7·2=7+7=14, а 3·2+4·2=(3+3)+(4+4)=6+8=14, следовательно, равенство (3+4)·2=3·2+4·2 верно.
4. Распределительное свойство умножения относительно вычитания:
умножить данную разность двух натуральных чисел на данное натуральное число – это все равно, что из произведения уменьшаемого и данного числа вычесть произведение вычитаемого и данного числа.
(a−b)·c=a·c−b·c
или a·(b−c)=a·b−a·c.
Проверим справедливость распределительного свойства умножения относительно вычитания на примере. Убедимся, что верно равенство 3·(4−2)=3·4−3·2. Так как 4−2=2, то произведение 3·(4−2) равно произведению 3·2, а 3·2=3+3=6. Теперь вычислим разность 3·4−3·2. Имеем 3·4−3·2=(3+3+3+3)−(3+3)=12−6=6. Таким образом, равенство 3·(4−2)=3·4−3·2 верное.
5. Свойство умножения единицы на натуральное число:
произведение любого натурального числа и единицы, равно самому этому числу.
n • 1 = n .
Например, произведение чисел 1 и 37 равно 37; результат умножения 1 и 1 004 есть число 1 004.
6. Свойство умножения нуля на натуральное число:
произведение любого натурального числа и нуля, равно нулю.
n • 0 = 0 .
0·1=0.
Произведение чисел 45 и 0 равно нулю. Если умножить 0 на 45 365, то тоже получим нуль.
Если вы хотите что-нибудь добавить на сайт «Спиши у Антошки», или у вас остались вопросы после прочтения материала, напишите мне info@spishy-u-antoshki.ru я с радостью нацарапаю вам ответ лапкой.

 Предыдущая Следующая
Предыдущая Следующая