Свойства параллелограмма в каком классе проходят

В этом разделе мы рассматриваем геометрический объект параллелограмм. Все элементы параллелограмма наследуются от четырехугольника, поэтому рассматривать их мы не будем. А вот свойства и признаки заслуживают детального рассмотрения. Мы разберем:
- чем признак отличается от свойства;
- рассмотрим основные свойства и признаки, которые изучают в программе 8 класса;
- сформулируем еще два дополнительных свойства, которые получим при решении опорных задач.
2.1 Определение параллелограмма
Чтобы правильно давать определения понятиям в геометрии, нужно не просто их заучивать, а понимать, как они формируются. В этом деле нам хорошо помогают схемы родовых понятий. Давайте посмотрим, что это такое.
Наш учебный модуль называется «Четырехугольники» и четырехугольник является ключевым понятием в этом курсе. Мы можем дать следующее определение четырехугольнику:
Четырёхугольник-это многоугольник, у которого четыре стороны и четыре вершины.
В этом определении родовым понятием будет многоугольник. Теперь дадим определение многоугольнику:
Многоугольником называется простая замкнутая ломаная вместе с частью плоскости, которую она ограничивает.
Ясно, что родовым понятием здесь выступает понятие ломаная. Если мы пойдем далее, то придем к понятию отрезка, а затем к конечным понятиям точка и прямая. Таким же образом мы можем продолжить нашу схему вниз:

Если мы потребуем, чтобы у четырехугольника две стороны были параллельны, а две нет, то мы получим фигуру, которая называется трапецией.
Трапеция – четырехугольник, у которого две стороны параллельны, а две другие — не параллельны.
А в случае, когда все противоположные стороны параллельны, мы имеем дело с параллелограммом.
Параллелограмм – четырехугольник, у которого противоположные стороны параллельны.
2.2 Cвойства параллелограмма
Свойство 1. В параллелограмме противоположные стороны равны и противоположные углы равны.

Докажем это свойство.
Дано: ABCD — параллелограмм.
Доказать: $angle A = angle C, angle B = angle D, AB = CD, AD = BC.$
Доказательство:
При доказательстве свойств любого геометрического объекта всегда вспоминаем его определение. Итак, параллелограмм – четырехугольник, у которого противоположные стороны параллельны. Ключевым моментом здесь выступает параллельность сторон.
Построим секущую ко всем четырем прямым. Такой секущей будет диагональ BD.

Очевидно, что нужно рассмотреть углы, образованные секущей и параллельными прямыми. Так как прямые параллельны, то накрест лежащие углы равны.
Теперь можно увидеть два равных треугольника по второму признаку.
Из равенства треугольников непосредственно следует первое свойство параллелограмма.
Свойство 2. Диагонали параллелограмма точкой пересечения делятся пополам.

Дано: ABCD — параллелограмм.
Доказать: $AO = OC, BO = OD.$
Доказательство:
Логика доказательства здесь такая же, как и в предыдущем свойстве: параллельность сторон и равенство треугольников. Первый шаг доказательства тот же, что у первого свойства.
Вторым шагом мы доказываем равенство треугольников по второму признаку. Обратите внимание, что равенство $BC=AD$ можно принять без доказательства (используя Свойство 1).
Из этого равенства следует, что $AO = OC, BO = OD.$

2.3 Опорная задача №4 (Свойство угла между высотами параллелограмма)

Дано: ABCD — параллелограмм, BK и BM — его высоты, $angle KBM = 60^0$.
Найти: $angle ABK$, $angle A$
Решение:
Приступая к решению этой задачи, нужно иметь ввиду следующее:
высота в параллелограмме перпендикулярна обеим противоположным сторонам
Например, если отрезок $BM$ проведен к стороне $DC$ и является его высотой ($BM perp DC$), то этот же отрезок будет высотой к противположной стороне ($BM perp BA$). Это следует из параллельности сторон $AB parallel DC$.

Далее мы можем найти $angle A$ из прямоугольного $bigtriangleup ABK$: $angle A = 90^0-30^0=60^0$

При решении этой задачи, ценным является свойство, которое мы получаем.
Дополнительное свойство. Угол между высотами параллелограмма, проведенными из его вершины, равен углу при соседней вершине.
2.4 Опорная задача №5 (Свойство биссектрисы параллелограмма)

Биссектриса угла А параллелограмма ABCD пересекает сторону BC в точке L, AD=12 см, AB =10 см.
Найти длину отрезка LC.
Решение:
- $angle 1 = angle 2$ (АК — биссектрисса);
- $angle 2 = angle 3$ (как накрест лежащие углы при $AD parallel BC$ и секущей АL);
- $angle 1 = angle 3$, $bigtriangleup ABL -$ равнобедренный.
Далее несложно найти длину отрезка LC = 2 см.
По ходу решения задачи мы получили свойство:
Дополнительное свойство. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
Предмет: геометрия 8.
Тема: Параллелограмм. Свойства параллелограмма.
Тип урока: урок открытия новых знаний.
Метод обучения: эвристический (постановка учебной задачи).
УМК под редакцией Л.С.Атанасяна
Класс: 8а, 2013-2014 учебный год.
Учитель Белогородцева Елена Александровна.
Цели урока:
Образовательная: познакомиться с понятием параллелограмма, сформулировать и доказать свойства параллелограмма.
Воспитательная: развивать инициативность, взаимопонимание, творческую активность, используя различные формы работы на уроке, умение работать в команде.
Развивающие: развивать наблюдательность, умение анализировать, сравнивать, делать выводы, контролировать свои действия.
Оборудование: проектор, экран, набор карточек для сбора заданий, карточки с заданием тестов, индивидуальные оценочные листы.
Характеристика исходных умений и навыков, необходимых для усвоения темы и постановки учебной задачи.
Учащиеся знают:
- понятие многоугольника, выпуклого и невыпуклого многоугольника;
- определение, свойства и признаки параллельных прямых;
- признаки равенства треугольников.
Учащиеся умеют:
- применять определение, свойства и признаки параллельных прямых при решении задач и доказательстве теорем;
- применять признаки равенства треугольников при решении задач и доказательстве теорем;
- пользоваться определением равных фигур.
Структура урока.
- Проверка домашнего задания (проводится с помощью проектора) (1 мин).
- Актуализация опорных знаний (10 мин)
- Формулировка проблемы, постановка учебной задачи (1 мин)
- Постановка темы и целей урока (1 мин)
- Открытие новых знаний и способов действий (8 мин)
- Первичное осмысление изученного и его применение в стандартных ситуациях (5 мин)
- Перенос знаний и их применение в новых, видоизмененных ситуациях (7 мин)
- Обобщение и систематизация новых знаний, способов действий (7 мин)
- Рефлексия учеником своих действий и самооценка (2 мин)
- Подведение итогов (2 мин)
- Постановка домашнего задания (1 мин)
Ход урока.
- Проверка домашнего задания: на экран проецируется слайд с домашним заданием, учащиеся проводят самооценку.
- Актуализация опорных знаний.
Задание 1 (работа в парах) (7 баллов)
Проверка правильности выполнения теста организуется с помощью проектора, учащиеся заносят полученное количество баллов в личную карточку (по одному баллу за каждое верно выполненное задание).
Задание 2 (7 баллов).
1 учащийся у доски с помощью карточек собирает свойства параллельных прямых и делает соответствующие рисунки;
1 учащийся у доски с помощью карточек собирает признаки параллельных прямых и делает соответствующие рисунки;
1 учащийся у доски с помощью карточек собирает признаки равенства треугольников и делает соответствующие рисунки;
1 учащийся у доски предложенные четырехугольники (3 разных выпуклых четырехугольника, параллелограмм, ромб, прямоугольник) разбивает на две группы:
1) противоположные стороны попарно параллельны,
- противоположные стороны не параллельны.
- Формулировка проблемы, постановка учебной задачи.
— По какому принципу четырехугольники разбиты на группы?
— 1 группа — противоположные стороны четырехугольника попарно параллельны,
— 2 группа – у четырехугольников противоположные стороны не параллельны.
Учитель предлагает учащимся начертить в тетради четырехугольник, у которого противоположные стороны попарно параллельны и дает название такого четырехугольника – параллелограмм.
- Постановка темы и цели урока.
Учитель предлагает учащимся сформулировать определение параллелограмма. Таким образом, учитель вместе с учащимися формулирует тему и цели урока.
Тема «Параллелограмм. Свойства параллелограмма»;
Цель урока: сформулировать определение параллелограмма, сформулировать и доказать свойства параллелограмма.
- Открытие новых знаний и способов действий.
Учащиеся разбиваются на группы по четыре человека. Каждая группа получает карточки с заданием (5 баллов):
- Измерьте стороны своих четырехугольников. Сделайте выводы. Проверьте правильность сделанных выводов в среде «Живая математика». Сформулируйте и докажите 1 свойство параллелограмма.
- Измерьте углы своих четырехугольников. Сделайте выводы. Проверьте правильность сделанных выводов в среде «Живая математика».
Сформулируйте и докажите 2 свойство параллелограмма.
- Проведите диагонали параллелограмма, точку пересечения обозначьте буквой О. Измерьте полученные отрезки. Сделайте выводы. Проверьте правильность сделанных выводов в среде «Живая математика». Сформулируйте и докажите 4 свойство параллелограмма.
Проверка работы группы осуществляется через презентацию.
- Первичное осмысление изученного и его применение в стандартных ситуациях.
Проводится эстафета по рядам (3 балла).
Задание 1.
Задание 2.
Является ли четырехугольник АВСD параллелограммом?
Задание 3.
Докажите, что в параллелограмме сумма углов, прилежащих к одной стороне, равна 180º.
С каждого ряда выходит 1 учащийся к доске и объясняет решение одной задачи.
- Перенос знаний и их применение в новых, видоизмененных ситуациях.
Проводится разноуровневая самостоятельная работа.
1 уровень (2 балла).
На рисунке MNǁPQ,
2 уровень (4 балла).
Дан параллелограмм АВСD. Найдите стороны и углы Δ АВD, если известно, что ВС=2 см, ВD=5 см, СD=4 см,
3 уровень (6 баллов).
Найдите стороны и углы Δ АВD, если известно, что ВD=3 дм, ВС на 2 дм больше, периметр Δ АВD равен 14 дм,
4 уровень (8 баллов).
Найдите стороны и углы параллелограмма АВСD, если известно, что его большая сторона на 3 м больше меньшей стороны, периметр параллелограмма равен 26 м, а больший угол в 3 раза больше меньшего угла.
5 уровень (10 баллов).
Найдите стороны и углы параллелограмма АВСD, если высота, проведенная к его большей стороне образует угол в 30º со смежной стороной параллелограмма и делит большую сторону на отрезки 3 см и 5 см.
Проводится взаимопроверка в парах.
- Обобщение и систематизация новых знаний, способов действий.
Учащиеся заполняют ЛОК №1
Чтобы ответить на поставленный вопрос в среде «Живая математика» выполните следующие задания (3 балла):
- Нарисуйте параллелограмм АВСD, в котором:
а) АD
б) ВС
в) АD>АВ,
г) ВС>АВ,
2) Нарисуйте параллелограмм АВСD, имеющий диагональ, которая:
а) короче каждой стороны;
б) длиннее каждой стороны;
в) равна одной из сторон;
г) равна каждой стороне.
3) Проверьте следующее утверждение «Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон».
- Рефлексия учеником своих действий и самооценка.
Учащиеся подсчитывают количество набранных за урок баллов, заносят результат в личную карту, переводят количество баллов в отметку:
отметка «5» ставится, если ученик набрал за урок 26 баллов и более;
отметка «4» ставится, если ученик набрал от 20 до 25 баллов;
отметка «3» ставится, если ученик набрал от 18 до 20 баллов;
отметка «2» ставится, если ученик набрал менее 18 баллов.
- Подведение итогов урока.
Учащиеся повторяют определение и свойства параллелограмма.
- Постановка домашнего задания.
Домашнее задание дается дифференцированно, в зависимости от той отметки, которую ученик получил на уроке:
п. 42;
«5» — №375, 376 (д); задача под запись: «Докажите, что в параллелограмме биссектрисы соседних углов перпендикулярны».
«4» — № 372 (б), 376 (в, д); задача под запись: «Докажите, что в параллелограмме биссектрисы противоположных углов параллельны или лежат на одной прямой».
«3», «2» — №372(в), 376 (в); задача под запись: «Через точку О пересечения диагоналей параллелограмма провели прямую. Она пересекает стороны параллелограмма в точках М и Р. Докажите, что точка О – середина отрезка МР».
творческое задание для всех: придумать задачу для соседа по парте.
Самоанализ урока.
На данном уроке учащиеся формулируют определение параллелограмма, формулируют и доказывают основные свойства параллелограмма. Это необходимо для дальнейшей работы с четырехугольниками и является базой для решения задач и доказательства теорем.
Данный урок является третьим уроком в теме «Четырехугольники». В ходе урока необходимо повторить свойства и признаки параллельных прямых, признаки равенства треугольников, сформулировать определение параллелограмма, сформулировать и доказать свойства параллелограмма.
Данный урок по типу – урок открытия новых знаний. Он включает в себя все основные этапы урока:
- Проверка домашнего задания (проводится с помощью проектора).
- Актуализация опорных знаний.
- Формулировка проблемы, постановка учебной задачи.
- Постановка темы и целей урока.
- Открытие новых знаний и способов действий.
- Первичное осмысление изученного и его применение в стандартных ситуациях.
- Перенос знаний и их применение в новых, видоизмененных ситуациях.
- Обобщение и систематизация новых знаний, способов действий.
- Рефлексия учеником своих действий и самооценка.
- Подведение итогов.
- Постановка домашнего задания.
При подготовке данного урока учитывались возрастные и индивидуальные особенности детей. Урок проводился в общеобразовательном классе, со средним качеством знаний учащихся, однако задания в основном выполнялись учащимися самостоятельно или в парах, были использованы игровые моменты и мультимедийная техника для поддержания интереса учащихся на уроке, самостоятельная работа учащихся была организована с учетом уровня усвоения знаний учащимися.
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
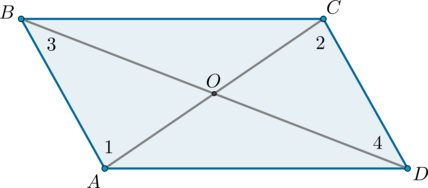
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
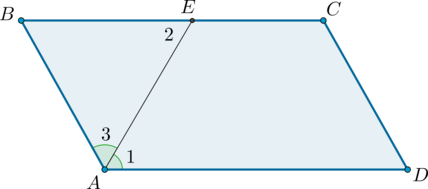
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
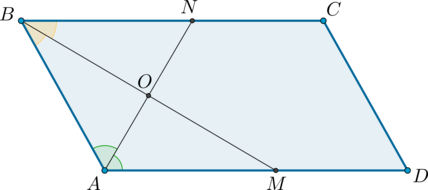
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ — (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).
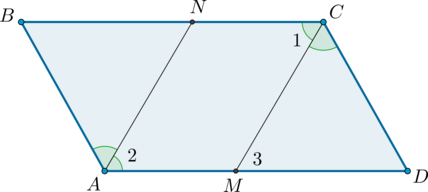
Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).
Замечание. Мы рассматриваем только выпуклые четырёхугольникивыпуклые четырёхугольники.
Свойства и признаки параллелограмма
| Тип утверждения | Фигура | Рисунок | Формулировка |
| Определение | Параллелограмм |  | Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны |
| Определение | Диагонали параллелограмма |  | Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины |
| Определение | Высота параллелограмма |  | Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение |
| Свойство | Равенство противолежащих сторон |  | Если четырёхугольник является параллелограммом, то его противолежащие стороны равны |
| Признак | Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом | ||
| Признак | Равенство и параллельность двух противолежащих сторон |  | Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом |
| Свойство | Диагонали точкой пересечения делятся пополам |  | Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам |
| Признак | Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом | ||
| Свойство | Суммы углов, прилежащих к сторонам |  | Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° |
| Признак | Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом | ||
| Свойство | Равенство противолежащих углов | Если четырёхугольник является параллелограммом, то его противолежащие углы равны | |
| Признак | Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом | ||
| Свойство | Два треугольника, на которые каждая диагональ делит четырёхугольник |  | Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника |
| Признак | Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом | ||
| Свойство | Четыре треугольника, на которые диагонали делят четырёхугольник |  | Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) |
| Признак | Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом |
| Определение: параллелограмм | |
 | Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны |
| Определение: диагонали параллелограмма | |
 | Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины |
| Определение: высота параллелограмма | |
 | Высотой параллелограмма называютперпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение |
| Свойство: равенство противолежащих сторон | |
 | Если четырёхугольник является параллелограммом, то его противолежащие стороны равны |
| Признак: равенство противолежащих сторон | |
 | Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом |
| Признак: равенство и параллельность двух противолежащих сторон | |
 | Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом |
| Свойство: диагонали точкой пересечения делятся пополам | |
 | Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам |
| Признак: диагонали точкой пересечения делятся пополам | |
 | Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом |
| Свойство: суммы углов, прилежащих к сторонам | |
 | Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180° |
| Признак: суммы углов, прилежащих к сторонам | |
 | Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом |
| Свойство: равенство противолежащих углов | |
 | Если четырёхугольник является параллелограммом, то его противолежащие углы равны |
| Признак: равенство противолежащих углов | |
 | Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом |
| Свойство: два треугольника, на которые каждая диагональ делит четырёхугольник | |
 | Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника |
| Признак: два треугольника, на которые каждая диагональ делит четырёхугольник | |
 | Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом |
| Свойство: четыре треугольника, на которые диагонали делят четырёхугольник | |
 | Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) |
| Признак: четыре треугольника, на которые диагонали делят четырёхугольник | |
 | Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом |
| Параллелограмм |
 Определение: Параллелограммом называют четырёхугольник, у которого противолежащие стороны параллельны |
| Диагонали параллелограмма |
 Определение: Диагональю параллелограмма называют отрезок, соединяющий противоположные вершины |
| Высота параллелограмма |
 Определение: Высотой параллелограмма называют перпендикуляр, опущенный из любой точки на стороне параллелограмма на противоположную сторону параллелограмма или ее продолжение |
| Равенство противолежащих сторон |
 Свойство: Если четырёхугольник является параллелограммом, то его противолежащие стороны равны. Признак: Если у четырёхугольника противолежащие стороны равны, то он является параллелограммом. |
| Равенство и параллельность двух противолежащих сторон |
 Признак: Если у четырёхугольника две противолежащие стороны равны и параллельны, то он является параллелограммом. |
| Диагонали точкой пересечения делятся пополам |
 Свойство: Если четырёхугольник является параллелограммом, то его диагонали точкой пересечения делятся пополам. Признак: Если у четырёхугольника диагонали точкой пересечения делятся пополам, то он является параллелограммом. |
| Суммы углов, прилежащих к сторонам |
 Свойство: Если четырёхугольник является параллелограммом, то сумма углов, прилежащих к любой его стороне равна 180°. Признак: Если у четырёхугольника сумма углов, прилежащих к любой его стороне равна 180°, то четырёхугольник является параллелограммом. |
| Равенство противолежащих углов |
 Свойство: Если четырёхугольник является параллелограммом, то его противолежащие углы равны. Признак: Если у четырёхугольника противолежащие углы равны, то четырёхугольник является параллелограммом. |
| Два треугольника, на которые каждая диагональ делит четырёхугольник |
 Свойство: Если четырёхугольник является параллелограммом, то каждая диагональ делит его на два равных треугольника. Признак: Если каждая диагональ четырёхугольника делит его на два равных треугольника, то четырёхугольник является параллелограммом. |
| Четыре треугольника, на которые диагонали делят четырёхугольник |
 Свойство: Если четырёхугольник является параллелограммом, то диагонали делит его на четыре треугольника равной площади (равновеликих треугольника) Признак: Если диагонали четырёхугольника делят его на четыре треугольника равной площади (равновеликих треугольника), то четырёхугольник является параллелограммом. |
Свойства и признаки прямоугольника
Свойства и признаки ромба
Свойства и признаки квадрата
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.



