Плотность это свойство какое
Пло́тность — скалярная физическая величина, определяемая как отношение массы тела к занимаемому этим телом объёму[1].
Для обозначения плотности обычно используется греческая буква ρ [ро] (происхождение обозначения подлежит уточнению), иногда используются также латинские буквы D и d (от лат. densitas «плотность»).
Более точное определение плотности требует уточнение формулировки:
- Средняя плотность тела — отношение массы тела к его объёму. Для однородного тела она также называется просто плотностью тела.
- Плотность вещества — это плотность однородного или равномерно неоднородного тела, состоящего из этого вещества.
- Плотность тела в точке — это предел отношения массы малой части тела (), содержащей эту точку, к объёму этой малой части (), когда этот объём стремится к нулю[2], или, записывая кратко, . При таком предельном переходе необходимо помнить, что на атомарном уровне любое тело неоднородно, поэтому необходимо остановиться на объёме, соответствующем используемой физической модели.
Поскольку масса в теле может быть распределена неравномерно, более адекватная модель определяет плотность в каждой точке тела как производную массы по объёму. Если учитывать точечные массы, то плотность можно определить как меру, либо как производную Радона — Никодима по отношению к некоторой опорной мере.
Виды плотности и единицы измерения[править | править код]
Исходя из определения плотности, её размерность представляет собой кг/м³ в СИ и г/см³ в системе СГС.
Для сыпучих и пористых тел различают:
- истинную плотность, определяемую без учёта пустот;
- удельную (кажущуюся) плотность, рассчитываемую как отношение массы вещества ко всему занимаемому им объёму. Истинную плотность из кажущейся получают с помощью величины коэффициента пористости — доли объёма пустот в занимаемом объёме. Для сыпучих тел удельная плотность называется насыпно́й плотностью.
Формула нахождения плотности[править | править код]
Плотность (плотность однородного тела или средняя плотность неоднородного) находится по формуле:
где m — масса тела, V — его объём;
формула является просто математической записью определения термина «плотность», данного выше.
- При вычислении плотности газов при нормальных условиях эта формула может быть записана и в виде:
где М — молярная масса газа, — молярный объём (при нормальных условиях приближённо равен 22,4 л/моль).
Плотность тела в точке записывается как
тогда масса неоднородного тела (тела с плотностью, зависящей от координат) рассчитывается как
Зависимость плотности от температуры[править | править код]
Как правило, при уменьшении температуры плотность увеличивается, хотя встречаются вещества, чья плотность в определённом диапазоне температур ведёт себя иначе, например, вода, бронза и чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.
Диапазон плотностей в природе[править | править код]
Для различных природных объектов плотность меняется в очень широком диапазоне.
- Самую низкую плотность имеет межгалактическая среда (2·10−31—5·10−31 кг/м³, без учёта тёмной материи)[3].
- Плотность межзвёздной среды приблизительно равна 10−23—10−21 кг/м³.
- Средняя плотность красных гигантов в пределах их фотосфер много меньше, чем у Солнца — из-за того, что их радиус в сотни раз больше при сравнимой массе.
- Плотность газообразного водорода (самого лёгкого газа) при нормальных условиях равна 0,0899 кг/м³.
- Плотность сухого воздуха при нормальных условиях составляет 1,293 кг/м³.
- Один из самых тяжёлых газов, гексафторид вольфрама, примерно в 10 раз тяжелее воздуха (12,9 кг/м³ при +20 °C)
- Жидкий водород при атмосферном давлении и температуре −253 °C имеет плотность 70 кг/м³.
- Плотность жидкого гелия при атмосферном давлении равна 130 кг/м³.
- Усреднённая плотность тела человека от 940—990 кг/м³ при полном вдохе, до 1010—1070 кг/м³ при полном выдохе.
- Плотность пресной воды при 4 °C 1000 кг/м³.
- Средняя плотность Солнца в пределах фотосферы около 1410 кг/м³, примерно в 1,4 раза выше плотности воды.
- Гранит имеет плотность 2600 кг/м³.
- Средняя плотность Земли равна 5520 кг/м³.
- Плотность железа равна 7874 кг/м³.
- Плотность металлического урана 19100 кг/м³.
- Плотность золота 19320 кг/м³.
- Самые плотные вещества при нормальных условиях — металлы платиновой группы. Имеют плотность 21400—22700 кг/м³.
- Плотность атомных ядер приблизительно 2·1017 кг/м³.
- Теоретически верхняя граница плотности по современным физическим представлениям это планковская плотность 5,1⋅1096 кг/м³.
Плотности астрономических объектов[править | править код]
Средняя плотность небесных тел Солнечной
системы (в г/см³)[4][5][6]
- Средние плотности небесных тел Солнечной системы см. на врезке.
- Межпланетная среда в Солнечной системе достаточно неоднородна и может меняться во времени, её плотность в окрестностях Земли ~10−21÷10−20 кг/м³.
- Плотность межзвёздной среды ~10−23÷10−21 кг/м³.
- Плотность межгалактической среды 2×10−34÷5×10−34 кг/м³.
- Средняя плотность красных гигантов на много порядков меньше из-за того, что их радиус в сотни раз больше, чем у Солнца.
- Плотность белых карликов 108÷1012 кг/м³
- Плотность нейтронных звёзд имеет порядок 1017÷1018 кг/м³.
- Средняя (по объёму под горизонтом событий) плотность чёрной дыры зависит от её массы и выражается формулой:
Средняя плотность падает обратно пропорционально квадрату массы чёрной дыры (ρ~M−2). Так, если чёрная дыра с массой порядка солнечной обладает плотностью около 1019 кг/м³, превышающей ядерную плотность (2×1017 кг/м³), то сверхмассивная чёрная дыра с массой в 109 солнечных масс (существование таких чёрных дыр предполагается в квазарах) обладает средней плотностью около 20 кг/м³, что существенно меньше плотности воды (1000 кг/м³).
Плотности некоторых газов[править | править код]
| Азот | 1,250 | Кислород | 1,429 |
| Аммиак | 0,771 | Криптон | 3,743 |
| Аргон | 1,784 | Ксенон | 5,851 |
| Водород | 0,090 | Метан | 0,717 |
| Водяной пар (100 °C) | 0,598 | Неон | 0,900 |
| Воздух | 1,293 | Радон | 9,81 |
| Гексафторид вольфрама | 12,9 | Углекислый газ | 1,977 |
| Гелий | 0,178 | Хлор | 3,164 |
| Дициан | 2,38 | Этилен | 1,260 |
Для вычисления плотности произвольного идеального газа, находящегося в произвольных условиях, можно использовать формулу, выводящуюся из уравнения состояния идеального газа:[7]
,
где:
Плотности некоторых жидкостей[править | править код]
Плотность некоторых пород древесины[править | править код]
| Бальса | 0,15 | Пихта сибирская | 0,39 |
| Секвойя вечнозелёная | 0,41 | Ель | 0,45 |
| Ива | 0,46 | Ольха | 0,49 |
| Осина | 0,51 | Сосна | 0,52 |
| Липа | 0,53 | Конский каштан | 0,56 |
| Каштан съедобный | 0,59 | Кипарис | 0,60 |
| Черёмуха | 0,61 | Лещина | 0,63 |
| Грецкий орех | 0,64 | Берёза | 0,65 |
| Вишня | 0,66 | Вяз гладкий | 0,66 |
| Лиственница | 0,66 | Клён полевой | 0,67 |
| Тиковое дерево | 0,67 | Бук | 0,68 |
| Груша | 0,69 | Дуб | 0,69 |
| Свитения (Махагони) | 0,70 | Платан | 0,70 |
| Жостер (крушина) | 0,71 | Тис | 0,75 |
| Ясень | 0,75 | Слива | 0,80 |
| Сирень | 0,80 | Боярышник | 0,80 |
| Пекан (кария) | 0,83 | Сандаловое дерево | 0,90 |
| Самшит | 0,96 | Эбеновое дерево | 1,08 |
| Квебрахо | 1,21 | Бакаут | 1,28 |
| Пробка | 0,20 |
Плотность некоторых металлов[править | править код]
Значения плотности металлов могут изменяться в весьма широких пределах: от наименьшего значения у лития, который легче воды, до наибольшего значения у осмия, который тяжелее золота и платины.
Измерение плотности[править | править код]
Для измерений плотности используются:
- Пикнометр — прибор для измерения истинной плотности
- Различные виды ареометров — измерители плотности жидкостей.
- Бурик Качинского и бур Зайдельмана — приборы для измерения плотности почвы.
- Вибрационный плотномер — прибор для измерения плотности жидкости и газа под давлением.
См. также[править | править код]
Видеоурок: плотность вещества
- Список химических элементов с указанием их плотности
- Удельный вес
- Удельная плотность
- Относительная плотность
- Объёмная плотность
- Конденсация
- Консистенция (лат. consistere — состоять) — состояние вещества, степень мягкости или плотности (твёрдости) чего-либо — полутвердых-полумягких веществ (масел, мыла, красок, строительных растворов и т. д.); наприм., глицерин имеет сиропообразную консистенцию.
- Консистометр — прибор для измерения в условных физических единицах консистенции различных коллоидных и желеобразных веществ, а также суспензий и грубодисперсных сред, к примеру, паст, линиментов, гелей, кремов, мазей.
- Концентрация частиц
- Концентрация растворов
- Плотность заряда
- Уравнение неразрывности
Примечания[править | править код]
- ↑ Существуют также поверхностная плотность (отношение массы к площади) и линейная плотность (отношение массы к длине), применяемые соответственно к плоским (двумерным) и вытянутым (одномерным) объектам.
- ↑ Подразумевается также, что область стягивается к точке, то есть, не только её объём стремится к нулю (что могло бы быть не только при стягивании области к точке, но, например, к отрезку), но также стремится к нулю и её диаметр (максимальный линейный размер).
- ↑ Агекян Т. А. . Расширение Вселенной. Модель Вселенной // Звёзды, галактики, Метагалактика. 3-е изд. / Под ред. А. Б. Васильева. — М.: Наука, 1982. — 416 с. — С. 249.
- ↑ Planetary Fact Sheet (англ.)
- ↑ Sun Fact Sheet (англ.)
- ↑ Stern, S. A., et al. The Pluto system: Initial results from its exploration by New Horizons (англ.) // Science : journal. — 2015. — Vol. 350, no. 6258. — P. 249—352. — doi:10.1126/science.aad1815.
- ↑ МЕХАНИКА. МОЛЕКУЛЯРНАЯ ФИЗИКА. Учебно-методическое пособие к лабораторным работам № 1-51, 1-61, 1-71, 1-72. Санкт-Петербургский Государственный Технологический Университет Растительных Полимеров (2014). Дата обращения 4 января 2019.
- ↑ Krebs, 2006, p. 158.
- ↑ Krebs, 2006, p. 136.
- ↑ Krebs, 2006, p. 96.
- ↑ Krebs, 2006, p. 160.
- ↑ Krebs, 2006, p. 138.
- ↑ Krebs, 2006, p. 198.
- ↑ Krebs, 2006, p. 319.
- ↑ 1 2 Krebs, 2006, p. 165.
- ↑ Krebs, 2006, p. 179.
- ↑ Krebs, 2006, p. 163.
- ↑ Krebs, 2006, p. 141.
- ↑ Krebs, 2006, p. 67.
- ↑ Krebs, 2006, p. 108.
- ↑ Krebs, 2006, p. 57.
- ↑ Krebs, 2006, p. 313.
- ↑ Krebs, 2006, p. 105.
- ↑ Krebs, 2006, p. 50.
- ↑ Krebs, 2006, p. 151.
- ↑ Krebs, 2006, p. 111.
- ↑ Krebs, 2006, p. 60.
- ↑ Krebs, 2006, p. 168.
- ↑ Krebs, 2006, p. 101.
- ↑ Krebs, 2006, p. 54.
- ↑ Krebs, 2006, p. 134.
- ↑ Krebs, 2006, p. 98.
- ↑ Krebs, 2006, p. 47.
Литература[править | править код]
- Плотность — статья из Большой советской энциклопедии. — М.: «Советская Энциклопедия», 1975. — Т. 20. — С. 49.
- Плотность — статья из Физической энциклопедии. Т. 3, С. 637.
- Krebs R. E. . The History and Use of Our Earth’s Chemical Elements: A Reference Guide. 2nd edition. — Westport: Greenwood Publishing Group, 2006. — xxv + 422 p. — ISBN 0-313-33438-2.
Ссылки[править | править код]
- Онлайн интерактивная таблица плотности веществ (рус.)
- Подробная таблица значений плотности распространенных жидкостей (рус.)
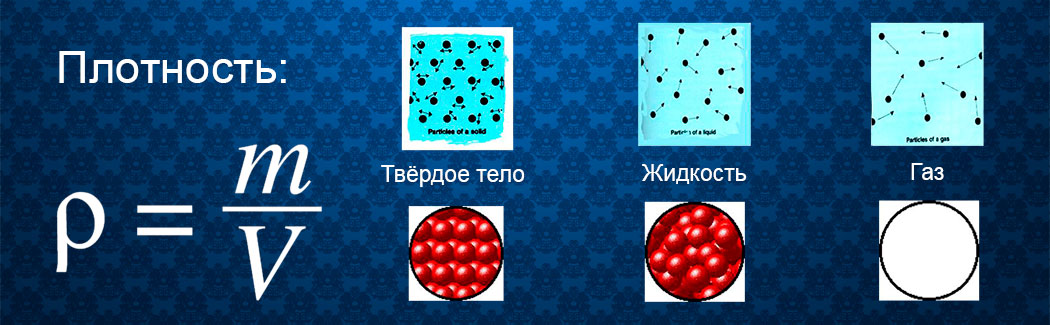
Плотность — это интенсивность распределения одной величины по другой.
Термин объединяет несколько различных понятий, таких как: плотность вещества; оптическая плотность; плотность населения; плотность застройки; плотность огня и многие другие. Рассмотрим два понятия, касающихся неразрушающего контроля.
1. Плотность вещества.
В физике плотностью вещества называют массу этого вещества, содержащуюся в единице объёма при нормальных условиях. Тела одинакового объёма, изготовленные из различных веществ, обладают различной массой, что и характеризует их плотность. К примеру, два куба одинаковых размеров, изготовленные из чугуна и алюминия, будут отличаться весом и плотностью.
Чтобы вычислить плотность какого-либо тела, нужно точно определить его массу и разделить её на точный объём этого тела.
кг/м3
— Единицы измерения
плотности в международной
системе единиц (СИ)
г/см3
— Единицы измерения
плотности в системе СГС
Выведем формулу вычисления плотности.
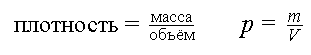
Для примера определим плотность бетона. Возьмём бетонный кубик весом 2,3 кг со стороной 10 см. Подсчитаем объём кубика.
Подставляем данные в формулу.
Получаем плотность 2 300 кг/м3.
Бетонный куб со стороной 10 см
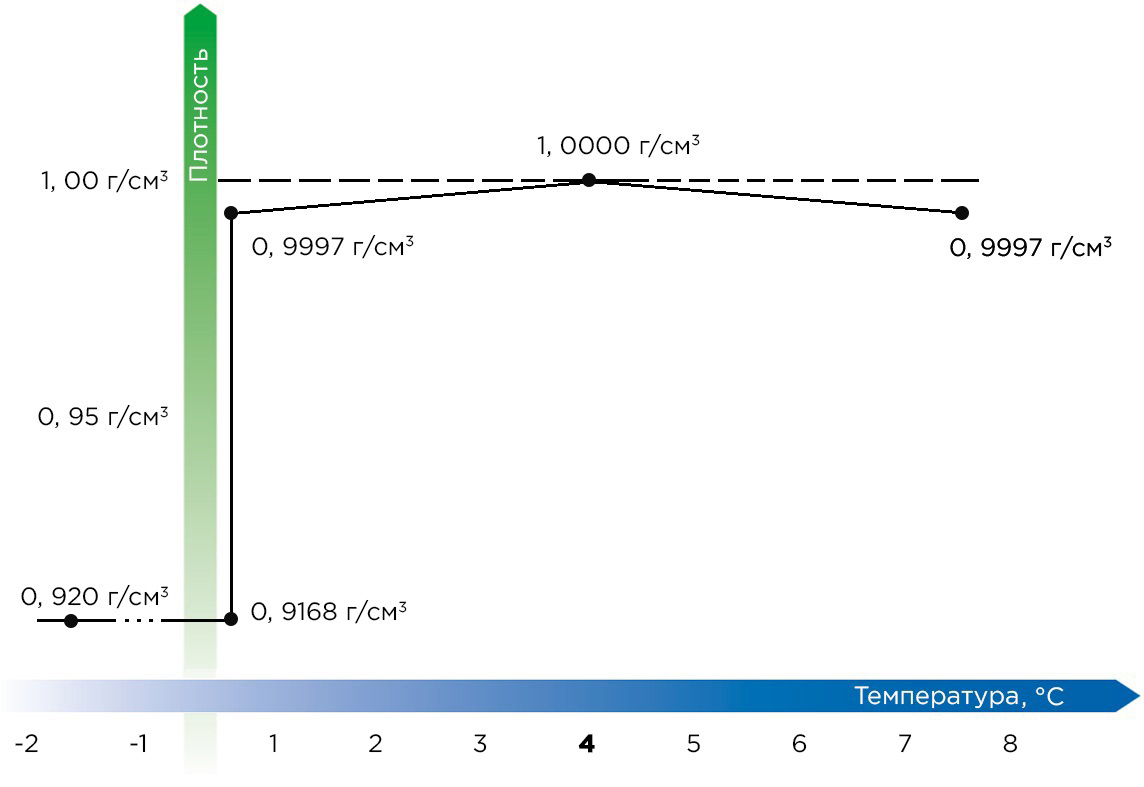График зависимости плотности воды от температуры
От чего зависит плотность вещества
Плотность вещества зависит от температуры. Так в подавляющем большинстве случаев при снижении температуры плотность увеличивается. Исключение составляют вода, чугун, бронза и некоторые другие вещества, которые в определённом температурном диапазоне проявляют себя иначе. Вода, например, имеет максимальную плотность при 4 °C. При повышении или понижении температуры плотность будет уменьшатся.
Плотность вещества меняется и при изменении его агрегатного состояния. Она скачкообразно растёт при переходе вещества из газообразного в жидкое состояние, и далее — в твёрдое. Здесь также есть исключения: плотность воды, висмута, кремния и некоторых других веществ снижается при затвердевании.
Чем измеряется плотность вещества
Для измерения плотности различных веществ применяются специальные приборы и приспособления. Так, плотность жидкостей и концентрация растворов измеряется различными ареометрами. Несколько разновидностей пикнометров предназначены для измерения плотности твёрдых тел, жидкостей и газов.
Металлический пикнометр
2. Оптическая плотность.
В физике оптической плотностью называют способность прозрачных материалов поглощать свет, а непрозрачных — отражать его. Это понятие в большинстве случаев характеризует степень ослабления светового излучения при прохождении его через слои и плёнки различных веществ.
Оптическую плотность принято выражать десятичным логарифмом отношения падающего на объект потока излучения к потоку, прошедшему через объект или отражённому от него:
D = lg (F0/F)
Оптическая плотность=логарифм (поток излучения, падающий на объект 
где D – оптическая плотность; F0 – поток излучения, падающий на объект; F – поток излучения, прошедший через объект или отражённый от него).
В радиографическом методе контроля оптическая плотность является одним из основных параметров, определяющих пригодность снимков для их расшифровки. Допустимые значения этого параметра обусловлены требованиями ГОСТ 7512-82 (раздел 6 – расшифровка снимков).
Оптическая плотность измеряется в Беллах, сокращённое обозначение — «Б». Для измерения оптической плотности используется денситометр. Прибор сравнивает яркость негатоскопа и яркость точки на плёнке. По этим двум значениям прибор определяет оптическую плотность. Чем выше плотность, тем темнее изображение.
Денситометр ДП 5004
Нашли ошибку в тексте? Выделите её и нажмите Ctrl + Enter, чтобы помочь нам её исправить.
Плотность — физическая величина, характеризующая физические свойства вещества, которая равна отношению массы тела к занимаемому этим телом объёму.
Плотность (плотность однородного тела или средняя плотность неоднородного) можно расчитать по формуле:
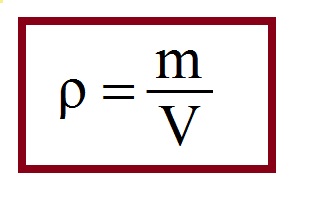
[ρ] = кг/м³; [m] = кг; [V] = м³.
где m — масса тела, V — его объём; формула является просто математической записью определения термина «плотность».
Все вещества состоят из молекул, следовательно масса всякого тела складывается из масс его молекул. Это подобно тому, как масса пакета с конфетами складывается из масс всех конфет в пакете. Если все конфеты одинаковы, то массу пакета с конфетами можно было бы определить, умножив массу одной конфеты на число конфет в пакете.
Молекулы чистого вещества одинаковы. Поэтому масса капли воды равна произведению массы одной молекулы воды на число молекул в капле.
Плотность вещества показывает, чему равна масса 1 м³ этого вещества.
Плотность воды равна 1000 кг/м³, значит, масса 1 м³ воды равна 1000 кг. Это число можно получить, умножив массу одной молекулы воды на число молекул, содержащихся в 1 м³ его объёма.
Плотность льда равна 900 кг/м³, это означает, что масса 1 м³ льда равна 900 кг.
Иногда используют единицу измерения плотности г/см³, поэтому ещё можно сказать, что масса 1см³ льда равна 0,9 г.
Каждое вещество занимает некоторый объём. И может оказаться, что объёмы двух тел равны, а их массы различны. В этом случае говорят, что плотности этих веществ различны.
Также при равенстве масс двух тел их объёмы будут различны. Например, объём льда почти в 9 раз больше объёма железного бруса.
Плотность вещества зависит от его температуры.
При повышении температуры обычно плотность уменьшается. Это связано с термическим расширением, когда при неизменной массе увеличивается объём.
При уменьшении температуры плотность увеличивается. Хотя существуют вещества, плотность которых в определённом диапазоне температур ведёт себя иначе. Например, вода, бронза, чугун. Так, плотность воды имеет максимальное значение при 4 °C и уменьшается как с повышением, так и с понижением температуры относительно этого значения.
При изменении агрегатного состояния плотность вещества меняется скачкообразно: плотность растёт при переходе из газообразного состояния в жидкое и при затвердевании жидкости. Вода, кремний, висмут и некоторые другие вещества являются исключениями из данного правила, так как их плотность при затвердевании уменьшается.
Источник
Решение задач
Задача №1.
Прямоугольная металлическая пластинка длиной 5 см, шириной 3 см и толщиной 5 мм имеет массу 85 г. Из какого материала она может быть иготовлена?
Анализ физической проблемы. Чтобы ответить на поставленный вопрос, необходимо определить плотность вещества, из которого изготовлена пластинка. Затем, воспользовавшись таблицей плотностей, определить – какому веществу соответствует найденое значение плотности. Эту задачу можно решить в данных единицах (т.е. без перевода в СИ).
Задача №2.
Медный шар объёмом 200 см3 имеет массу 1,6 кг. Определите, цельный этот шар или пустой. Если шар пустой, то определите объём полости.
Анализ физической проблемы. Если объём меди меньше объёма шара Vмед<Vш, то шар пустой. Понятно, что объём пустоты Vпуст = Vш – Vмед . Чтобы найти объём пустоты, выясним, какой объём занимает в шаре медь. Плотность меди найдём в таблице. В этой задаче следует массу подать в граммах, объём – в сантиметрах кубических, плотность, соответственно, – в г/см3.
Задача №3.
Канистра, которая вмещает 20 кг воды, наполнили бензином. Определите массу бензина в канистре.
Анализ физической проблемы. Для определения массы бензина в канистре нам необходимо найти плотность бензина и ёмкость канистры, которая равна объёму воды. Объём воды определим по её массе и плотности. Плотность воды и бензина найдём в таблице. Задачу лучше решать в единицах СИ.
Задача №4.
Из 800 см3 олова и 100 см3 свинца изготовили сплав. Какова его плотность? Каково отношение масс олова и свинца в сплаве?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 22 декабря 2019;
проверки требуют 2 правки.
Пло́тность вероя́тности — один из способов задания распределения случайной величины. Во многих практических приложениях понятия «плотность вероятности» и «плотность (распределения) случайной величины» или «функция распределения вероятностей» фактически синонимизируются и под ними подразумевается вещественная функция, характеризующая сравнительную вероятность реализации тех или иных значений случайной переменной (переменных).
Прикладное описание понятия[править | править код]
Плотность распределения одномерной непрерывной случайной величины — это числовая функция , отношение значений которой в точках и задаёт отношение вероятностей попаданий величины в узкие интервалы равной ширины и вблизи данных точек.
Плотность распределения неотрицательна при любом и нормирована, то есть
При стремлении к функция стремится к нулю. Размерность плотности распределения всегда обратная к размерности случайной величины — если исчисляется в метрах, то размерностью будет м-1.
Если в конкретной ситуации известно выражение для , с его помощью можно вычислить вероятность попадания величины в интервал как
.
Зная плотность вероятности, можно также определить наиболее вероятное значение (моду) случайной величины как максимум .
Также с помощью плотности вероятности находится среднее значение случайной величины:
и среднее значение измеримой функции случайной величины:
.
Чтобы перейти к плотности распределения другой случайной величины , нужно взять
,
где — обратная функция по отношению к (предполагается, что z — взаимно однозначное отображение).
Значение плотности распределения не является вероятностью принять случайной величиной значение . Так, вероятность принятия непрерывной случайной величиной значения равна нулю. При непрерывном распределении случайной величины вопрос может ставиться о вероятности её попадания в некий диапазон, а не о вероятности реализации её конкретного значения.
Интеграл
называют функцией распределения (соответственно, плотность распределения вероятности — это производная функции распределения). Функция является неубывающей и изменяется от 0 при до 1 при . На практике часто допускается неточность терминологии, то есть плотность распределения , как и , именуется функцией распределения (иногда законом распределения), но обычно из контекста очевидно, о чём идёт речь.[источник не указан 119 дней]
Самым простым распределением является равномерное распределение на отрезке . Для него плотность вероятности равна:
Широко известным распределением является «нормальное», оно же гауссово, плотность которого записывается как
,
где и — параметры: математическое ожидание и среднеквадратичное отклонение. Другие примеры плотностей распределения — одностороннее лапласовское ():
и ,
и максвелловское ():
и .
В двух последних примерах множитель подбирается в зависимости от параметра или так, чтобы обеспечить нормировку интеграла от плотности вероятности. В случае распределения Лапласа оказывается, что .
Как названные, так и другие распределения широко применяются в физике. Например, в случае распределения Максвелла роль случайной величины обычно играет абсолютная величина скорости молекулы в идеальном газе. При этом для аргумента функции нередко используют тот же символ, что и для рассматриваемой в физической задаче случайной величины (как если бы выше на месте всюду стояло ). Так, в выражении максвелловской плотности распределения пишут не формальную переменную , а символ скорости . В простейших ситуациях такая вольность с обозначениями не приводит к недоразумениям.
Выше была изложена суть понятия «плотность вероятности». Однако, такое изложение не является строгим — плотность нередко является функцией нескольких величин, в рассуждениях неявно предполагались не всегда гарантируемые непрерывность и дифференцируемость функций и так далее.
Определение плотности вероятности в теории меры[править | править код]
Плотность вероятности можно рассматривать как один из способов задания вероятностной меры на евклидовом пространстве .
Пусть является вероятностной мерой на , то есть определено вероятностное пространство , где обозначает борелевскую σ-алгебру на . Пусть обозначает меру Лебега на .
Вероятность называется абсолютно непрерывной (относительно меры Лебега) (), если любое борелевское множество нулевой меры Лебега также имеет вероятность ноль:
Если вероятность абсолютно непрерывна, то согласно теореме Радона-Никодима существует неотрицательная борелевская функция такая, что
,
где использовано общепринятое сокращение , и интеграл понимается в смысле Лебега.
В более общем виде, пусть — произвольное измеримое пространство, а и — две меры на этом пространстве. Если найдется неотрицательная , позволяющая выразить меру через меру в виде
то такую функцию называют плотностью меры по мере , или производной Радона-Никодима меры относительно меры , и обозначают
.
Плотность случайной величины[править | править код]
Пусть определено произвольное вероятностное пространство , и случайная величина (или случайный вектор). индуцирует вероятностную меру на , называемую распределением случайной величины .
Если распределение абсолютно непрерывно относительно меры Лебега, то его плотность называется плотностью случайной величины . Сама случайная величина называется абсолютно непрерывной.
Таким образом для абсолютно непрерывной случайной величины имеем:
.
Замечания[править | править код]
- Не всякая случайная величина абсолютно непрерывна. Любое дискретное распределение, например, не является абсолютно непрерывным относительно меры Лебега, а потому дискретные случайные величины не имеют плотности.
- Функция распределения абсолютно непрерывной случайной величины непрерывна и может быть выражена через плотность следующим образом:
.
В одномерном случае:
.
Если , то , и
.
В одномерном случае:
.
- Математическое ожидание функции от абсолютно непрерывной случайной величины может быть записано в виде:
,
где — борелевская функция, так что определено и конечно.
Плотность преобразования случайной величины[править | править код]
Пусть — абсолютно непрерывная случайная величина, и — инъективная непрерывно дифференцируемая функция такая, что , где — якобиан функции в точке . Тогда случайная величина также абсолютно непрерывна, и её плотность имеет вид:
.
В одномерном случае:
.
Свойства плотности вероятности[править | править код]
- Интеграл от плотности по всему пространству равен единице:
.
Обратно, если — неотрицательная почти всюду функция, такая что , то существует абсолютно непрерывная вероятностная мера на такая, что является её плотностью.
- Замена меры в интеграле Лебега:
,
где любая борелевская функция, интегрируемая относительно вероятностной меры .
Примеры абсолютно непрерывных распределений[править | править код]
См. также[править | править код]
- Распределение вероятностей
- Сингулярное распределение
- Функция вероятности
Литература[править | править код]
- Плотность вероятности // Большая российская энциклопедия : [в 35 т.] / гл. ред. Ю. С. Осипов. — М. : Большая российская энциклопедия, 2004—2017.