На каком свойстве основано сокращение дробей
Основное свойство дроби
Все обыкновенные дроби обладают основным свойством дроби:
Замечание 1
Если числитель и знаменатель дроби будет умножен или разделен на одно и то же натуральное число, то в результате получим дробь, равную исходной:
$frac{acdot n}{bcdot n}=frac{a}{b}$
и
$frac{adiv n}{bdiv n}=frac{a}{b}$
Пример 1
Пусть дан квадрат, разбитый на $4$ равных части. Если закрасить $2$ из $4$ частей, получим закрашенные $frac{2}{4}$ всего квадрата. Если посмотреть на данный квадрат, то очевидно, что закрашена ровно его половина, т.е. ${1}{2}$. Таким образом, получаем $frac{2}{4}=frac{1}{2}$. Разложим числа $2$ и $4$ на множители:
$2=1cdot 2$,
$4=2cdot 2$.
Подставим эти разложения в равенство:
$frac{1}{2}=frac{2}{4}$,
$frac{1}{2}=frac{1cdot 2}{2cdot 2}$,
$frac{1}{2}=frac{2div 2}{4div 2}$.
Пример 2
Можно ли получить равную дробь, если и числитель, и знаменатель заданной дроби умножить на $18$, а затем разделить на $3$?
Решение.
Пусть дана некоторая обыкновенная дробь $frac{a}{b}$. По условию числитель и знаменатель этой дроби умножили на $18$, получили:
$frac{acdot 18}{bcdot 18}$
Согласно основному свойству дроби:
$frac{acdot 18}{bcdot 18}=frac{a}{b}$
Далее по условию числитель и знаменатель разделили на $3$:
$frac{adiv 3}{bdiv 3}$
Согласно основному свойству дроби:
$frac{adiv 3}{bdiv 3}=frac{a}{b}$
Таким образом, получили в результате дробь, равную исходной.
Ответ: Можно получить дробь, равную исходной.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Применение основного свойства дроби
Основное свойство дроби чаще всего применяют для:
- приведения дробей к новому знаменателю:
- сокращения дробей.
Приведение дроби к новому знаменателю – замена заданной дроби такой дробью, которая будет ей равна, но иметь больше числитель и больше знаменатель. Для этого числитель и знаменатель дроби умножают на одно и то же натуральное число, в результате чего по основному свойству дроби получают дробь, равную исходной, но с большими числителем и знаменателем.
Сокращение дроби – замена заданной дроби такой дробью, которая будет ей равна, но иметь меньший числитель и меньший знаменатель. Для этого числитель и знаменатель дроби делят на положительный общий делитель числителя и знаменателя, отличный от нуля, в результате чего по основному свойству дроби получают дробь, равную исходной, но с меньшими числителем и знаменателем.
Если разделить (сократить) числитель и знаменатель на их НОД, то в результате получают несократимый вид исходной дроби.
Сокращение дробей
Как известно, обыкновенные дроби делятся на сократимые и несократимые.
Для сокращения дроби нужно выполнить деление и числителя, и знаменателя дроби на их положительный общий делитель, не равный нулю. При сокращении дроби получают новую дробь с меньшим числителем и знаменателем, по основному свойству дроби равную исходной.
Пример 3
Сократить дробь $frac{15}{25}$.
Решение.
Сократим дробь на $5$ (разделим ее числитель и знаменатель на $5$):
$frac{15}{25}=frac{15div 5}{25div 5}=frac{3}{5}$
Ответ: $frac{15}{25}=frac{3}{5}$.
Получение несократимой дроби
Чаще всего дробь сокращают для получения несократимой дроби, равной исходной сократимой дроби. Такого результата можно достичь, если разделить и числитель, и знаменатель исходной дроби на их НОД.
$frac{adiv НОД (a,b)}{bdiv НОД (a,b)}$ – несократимая дробь, т.к. согласно свойствам НОД числитель и знаменатель данной дроби – взаимно простые числа.
НОД(a,b) – наибольшее число, на которое можно разделить и числитель, и знаменатель дроби $frac{a}{b}$.
Таким образом, для приведения дроби к несократимому виду необходимо ее числитель и знаменатель разделить на их НОД.
Замечание 2
Правило сокращения дроби:
1. Найти НОД двух чисел, которые стоят в числителе и знаменателе дроби.
2. Выполнить деление числителя и знаменателя дроби на найденный НОД.
Пример 4
Привести дробь $6/36$ к несократимому виду.
Решение.
Сократим данную дробь на НОД$(6,36)=6$, т.к. $36div 6=6$. Получим:
$frac{6}{36}=frac{6div 6}{36div 6}=frac{1}{6}$
Ответ: $frac{6}{36}=frac{1}{6}$.
Практически фраза «сократить дробь» подразумевает, что нужно привести дробь к несократимому виду.
Сокращение дробей нужно для того, чтобы привести дробь к более простому виду, например, в ответе полученном в результате решения выражения.
Сокращение дробей, определение и формула.
Что такое сокращение дробей? Что значит сократить дробь?
Определение:
Сокращение дробей – это разделение у дроби числитель и знаменатель на одно и то же положительное число не равное нулю и единице. В итоге сокращения получается дробь с меньшим числителем и знаменателем, равная предыдущей дроби согласно основному свойству рациональных чисел.
Формула сокращения дробей основного свойства рациональных чисел.
(frac{p times n}{q times n}=frac{p}{q})
Рассмотрим пример:
Сократите дробь (frac{9}{15})
Решение:
Мы можем разложить дробь на простые множители и сократить общие множители.
(frac{9}{15}=frac{3 times 3}{5 times 3}=frac{3}{5} times color{red} {frac{3}{3}}=frac{3}{5} times 1=frac{3}{5})
Ответ: после сокращения получили дробь (frac{3}{5}). По основному свойству рациональных чисел первоначальная и получившееся дробь равны.
(frac{9}{15}=frac{3}{5})
Как сокращать дроби? Сокращение дроби до несократимого вида.
Чтобы нам получить в результате несократимую дробь, нужно найти наибольший общий делитель (НОД) для числителя и знаменателя дроби.
Есть несколько способов найти НОД мы воспользуемся в примере разложением чисел на простые множители.
Получите несократимую дробь (frac{48}{136}).
Решение:
Найдем НОД(48, 136). Распишем числа 48 и 136 на простые множители.
48=2⋅2⋅2⋅2⋅3
136=2⋅2⋅2⋅17
НОД(48, 136)= 2⋅2⋅2=6
(frac{48}{136}=frac{color{red} {2 times 2 times 2} times 2 times 3}{color{red} {2 times 2 times 2} times 17}=frac{color{red} {6} times 2 times 3}{color{red} {6} times 17}=frac{2 times 3}{17}=frac{6}{17})
Ответ: (frac{6}{17}) несократимая дробь.
Правило сокращения дроби до несократимого вида.
- Нужно найти наибольший общий делитель для числители и знаменателя.
- Нужно поделить числитель и знаменатель на наибольший общий делитель в результате деления получить несократимую дробь.
Пример:
Сократите дробь (frac{152}{168}).
Решение:
Найдем НОД(152, 168). Распишем числа 152 и 168 на простые множители.
152=2⋅2⋅2⋅19
168=2⋅2⋅2⋅3⋅7
НОД(152, 168)= 2⋅2⋅2=6
(frac{152}{168}=frac{color{red} {6} times 19}{color{red} {6} times 21}=frac{19}{21})
Ответ: (frac{19}{21}) несократимая дробь.
Сокращение неправильной дроби.
Как сократить неправильную дробь?
Правила сокращения дробей для правильных и неправильных дробей одинаковы.
Рассмотрим пример:
Сократите неправильную дробь (frac{44}{32}).
Решение:
Распишем на простые множители числитель и знаменатель. А потом общие множители сократим.
(frac{44}{32}=frac{color{red} {2 times 2 } times 11}{color{red} {2 times 2 } times 2 times 2 times 2}=frac{11}{2 times 2 times 2}=frac{11}{8})
Сокращение смешанных дробей.
Смешанные дроби по тем же правилам что и обыкновенные дроби. Разница лишь в том, что мы можем целую часть не трогать, а дробную часть сократить или смешанную дробь перевести в неправильную дробь, сократить и перевести обратно в правильную дробь.
Рассмотрим пример:
Сократите смешанную дробь (2frac{30}{45}).
Решение:
Решим двумя способами:
Первый способ:
Распишем дробную часть на простые множители, а целую часть не будем трогать.
(2frac{30}{45}=2frac{2 times color{red} {5 times 3}}{3 times color{red} {5 times 3}}=2frac{2}{3})
Второй способ:
Переведем сначала в неправильную дробь, а потом распишем на простые множители и сократим. Полученную неправильную дробь переведем в правильную.
(2frac{30}{45}=frac{45 times 2 + 30}{45}=frac{120}{45}=frac{2 times color{red} {5 times 3} times 2 times 2}{3 times color{red} {3 times 5}}=frac{2 times 2 times 2}{3}=frac{8}{3}=2frac{2}{3})
Вопросы по теме:
Можно ли сокращать дроби при сложении или вычитании?
Ответ: нет, нужно сначала сложить или вычесть дроби по правилам, а только потом сокращать. Рассмотрим пример:
Вычислите выражение (frac{50+20-10}{20}) .
Решение:
Часто допускают ошибку сокращая одинаковые числа в числителе и знаменателе в нашем случаем число 20, но их сокращать нельзя пока не выполните сложение и вычитание.
(frac{50+color{red} {20}-10}{color{red} {20}}=frac{60}{20}=frac{3 times 20}{20}=frac{3}{1}=3)
На какие числа можно сокращать дробь?
Ответ: можно сокращать дробь на наибольший общий делитель или обычный делитель числителя и знаменателя. Например, дробь (frac{100}{150}).
Распишем на простые множители числа 100 и 150.
100=2⋅2⋅5⋅5
150=2⋅5⋅5⋅3
Наибольшим общим делителем будет число НОД(100, 150)= 2⋅5⋅5=50
(frac{100}{150}=frac{2 times 50}{3 times 50}=frac{2}{3})
Получили несократимую дробь (frac{2}{3}).
Но необязательно всегда делить на НОД не всегда нужна несократимая дробь, можно сократить дробь на простой делитель числителя и знаменателя. Например, у числа 100 и 150 общий делитель 2. Сократим дробь (frac{100}{150}) на 2.
(frac{100}{150}=frac{2 times 50}{2 times 75}=frac{50}{75})
Получили сократимую дробь (frac{50}{75}).
Какие дроби можно сокращать?
Ответ: сокращать можно дроби у которых числитель и знаменатель имеют общий делитель. Например, дробь (frac{4}{8}). У числа 4 и 8 есть число, на которое они оба делятся это число 2. Поэтому такую дробь можно сократить на число 2.
Пример:
Сравните две дроби (frac{2}{3}) и (frac{8}{12}).
Эти две дроби равны. Рассмотрим подробно дробь (frac{8}{12}):
(frac{8}{12}=frac{2 times 4}{3 times 4}=frac{2}{3} times frac{4}{4}=frac{2}{3} times 1=frac{2}{3})
Отсюда получаем, (frac{8}{12}=frac{2}{3})
Две дроби равны тогда и только тогда, когда одна из них получена путем сокращения другой дроби на общий множитель числителя и знаменателя.
Пример:
Сократите если возможно следующие дроби: а) (frac{90}{65}) б) (frac{27}{63}) в) (frac{17}{100}) г) (frac{100}{250})
Решение:
а) (frac{90}{65}=frac{2 times color{red} {5} times 3 times 3}{color{red} {5} times 13}=frac{2 times 3 times 3}{13}=frac{18}{13})
б) (frac{27}{63}=frac{color{red} {3 times 3} times 3}{color{red} {3 times 3} times 7}=frac{3}{7})
в) (frac{17}{100}) несократимая дробь
г) (frac{100}{250}=frac{color{red} {2 times 5 times 5} times 2}{color{red} {2 times 5 times 5} times 5}=frac{2}{5})
1
Урок Сокращение дробей www.konspekturoka.ru
2
ввести понятие сокращения дробей и дать определение несократимой дроби; ввести понятие сокращения дробей и дать определение несократимой дроби; учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби ввести понятие сокращения дробей и дать определение несократимой дроби; ввести понятие сокращения дробей и дать определение несократимой дроби; учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби учить сокращать дроби, используя признаки делимости чисел и основное свойство дроби 2www.konspekturoka.ru
3
На основании чего мы можем умножать числитель и знаменатель дроби? На основании основного свойства дроби мы можем умножать числитель и знаменатель дроби www.konspekturoka.ru
4
На какие числа можно разделить числитель и знаменатель дроби? На 2, 3, 4, 6, 12. Если разделить числитель и знаменатель дроби на наибольший общий делитель, на 12. Какая дробь получится? = Определение. Деление числителя и знаменателя на их общий делитель, отличный от единицы, называют сокращением дроби. Определение. При сокращении дроби ее числовое значение не меняете изменилась только ее запись www.konspekturoka.ru
5
Что можно сказать о числах 2 и 3? Если дробь больше сократить нельзя, то ее называют несократимой Они взаимно простые Определение. Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой. Дробь, числитель и знаменатель которой взаимно простые числа, называется несократимой www.konspekturoka.ru
6
1. Сократить числитель и знаменатель на их НОД : : : : == 2. Последовательно сокращать на общие делители = = == 3. Разложить числитель и знаменатель на множители, а потом сократить = = www.konspekturoka.ru
7
Назвать несократимую дробь. Почему эти дроби являются несократимыми? www.konspekturoka.ru
8
www.konspekturoka.ru8 Назовите наибольший делитель числителя и знаменателя. Разделите числитель и знаменатель данной дроби на их общий делитель. Как называется получившаяся дробь? 4 6 = =54 70 а 140 а =12 35 п 21 п =53 наибольший делитель числителя и знаменателя — 2 наибольший делитель числителя и знаменателя — 3 наибольший делитель числителя и знаменателя — 70 а наибольший делитель числителя и знаменателя – 7 п
9
Какую часть часа составляют 45 мин, 12 мин, 15 мин, 40 мин, 35 мин? www.konspekturoka.ru
10
Сократите дробь: Общий делитель 3 с. Числитель и знаменатель дроби представим в виде множителей: Назовите общий делитель числителя и знаменателя: Общий делитель 25b. Общий делитель 3bc www.konspekturoka.ru
11
www.konspekturoka.ru11 Сократите дроби:
12
Найдите среди чисел 1, 3, 10, 12, 13, 15, 16, 39 пары взаимно простых чисел. 1 и 3; 1 и 10; 1 и 12; 1 и 13; 1 и 15; 1 и 16; 1 и 39; 3 и 10; 3 и 13; 3 и 16; 10 и 13; 10 и 39; 12 и 13; 13 и 15; 13 и 16; 15 и 16; 16 и www.konspekturoka.ru
13
Представить в виде обыкновенной несократимой дроби: 0,2 = 0,8 = 0,5 = 0,15 = 0,24 = 0,35 = 0,75 = 0,05 = 0,125 = 0,025 = 0,008 = 0,375 = www.konspekturoka.ru
14
www.konspekturoka.ru14 17 · ·51 48 · · · · · 5 4 · 3 = = = 3 · 2 1 · 1 =61 = = 3 · 2 4 · 5 2 1=
15
www.konspekturoka.ru15 22 · · 33 6·15·4 18·27·10 82·15·16 12·41· = 2 · 1 3 · 3 = = 1·5·2 3·9·5 1 1= 1·1·2 3·9·1 = = 2·3·4 3·1·4 = ·1·1 1·1·1 =21 = 2
16
а·b b·cb·cb·cb·c n·8m 12b·n а·d·c d·c·k 3 3 = 1 1 ас =а·1 1·c = а·1·1 1·1·k =аk = 1·2m 3b·1 =2m3b www.konspekturoka.ru
17
19·11+19·5 38·20-38·8 = 19·(11+5) 38·(20-8) а·5 b 25c·18 a = 8·1·1·b 5· c·6·1 =8b30c = 19·16 38·12 = = ·4 2·32·32·32·3 1 2= 1·2 1·31·31·31·3 = www.konspekturoka.ru
18
Какую часть килограмма составляют 125 г, 250 г, 750 г? 125 г, 250 г, 750 г? Сколько граммов в 1 кг? 125 г = 250 г = 750 г = www.konspekturoka.ru
19
www.konspekturoka.ru Что значит сократить дробь? Что значит сократить дробь? Что меняется при сокращении дробей? Что меняется при сокращении дробей? В каком случае дробь будет несократимой? В каком случае дробь будет несократимой? Какую дробь называют несократимой? Какую дробь называют несократимой? Приведите примеры несократимой дроби. Приведите примеры несократимой дроби. На каком свойстве основано сокращение дробей? На каком свойстве основано сокращение дробей?
В данной статье разберем, в чем заключается основное свойство дроби, сформулируем его, приведем доказательство и наглядный пример. Затем рассмотрим, как применять основное свойство дроби при совершении действий сокращения дробей и приведения дробей к новому знаменателю.
Основное свойство дроби, формулировка, доказательство и примеры
Все обыкновенные дроби обладают важнейшим свойством, которое мы и называем основным свойством дроби, и звучит оно следующим образом:
Определение 1
Если числитель и знаменатель одной дроби умножить или разделить на одно и то же натуральное число, то в итоге получится дробь, равная заданной.
Представим основное свойство дроби в виде равенства. Для натуральных чисел a, b и mбудут справедливыми равенства:
a·mb·m=ab и a:mb:m=ab
Рассмотрим доказательство основного свойства дроби. Опираясь на свойства умножения натуральных чисел и свойства деления натуральных чисел, запишем равенства: (a · m) · b = (b · m) · a и (a : m) · b = (b : m) · a. Таким образом, дроби a·mb·m и ab, а также a:mb:m и ab являются равными по определению равенства дробей.
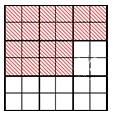
Разберем пример, который графически проиллюстрирует основное свойство дроби.
Пример 1
Допустим, у нас есть квадрат, разделенный на 9 «больших» частей-квадратов. Каждый «большой» квадрат разделен на 4 меньших по размеру. Возможно сказать, что заданный квадрат поделен на 4·9 = 36 «маленьких» квадратов. Выделим цветом 5 «больших» квадратов. При этом окрашенными будут 4·5 = 20 «маленьких» квадратов. Покажем рисунок, демонстрирующий наши действия:

Окрашенная часть – это 59 исходной фигуры или 2036, что является тем же самым. Таким образом, дроби 59 и 2036 являются равными: 59=2036 или 2036=59.
Эти равенства, а также равенства 20 = 4·5, 36 = 4·9, 20:4 = 5 и 36:4 = 9 дают возможность сделать вывод, что 59=5·49·4 и 2036=20·436·4.
Чтобы закрепить теорию, разберем решение примера.
Пример 2
Задано, что числитель и знаменатель некоторой обыкновенной дроби умножили на 47, после чего эти числитель и знаменатель разделили на 3. Равна ли полученная в итоге этих действий дробь заданной?
Решение
Опираясь на основное свойство дроби, можно говорить о том, что умножение числителя и знаменателя заданной дроби на натуральное число 47 даст в результате дробь, равную исходной. То же самое мы можем утверждать, производя дальнейшее деление на 3. В конечном счете мы получим дробь, равную заданной.
Ответ: да, полученная в итоге дробь будет равна исходной.
Применение основного свойства дроби
Основное свойство применяется, когда нужно привести дроби к новому знаменателю и при сокращении дробей.
Приведение дроби к новому знаменателю – это действие замены заданной дроби равной ей дробью, но с большими числителем и знаменателем. Чтобы привести дробь к новому знаменателю, нужно умножить числитель и знаменатель дроби на необходимое натуральное число. Действия с обыкновенными дробями были бы невозможны без способа приводить дроби к новому знаменателю.
Определение 2
Сокращение дроби – действие перехода к новой дроби, равной заданной, но с меньшими числителем и знаменателем. Чтобы сократить дробь, нужно разделить числитель и знаменатель дроби на одно и то же необходимое натуральное число, которое будет называться общим делителем.
Возможны случаи, когда подобного общего делителя нет, тогда говорят о том, что исходная дробь несократима или не подлежит сокращению. В частности, сокращение дроби при помощи наибольшего общего делителя приведет дробь к несократимому виду.
