На каком свойстве основано правило приведения дробей к ноз

В данной статье рассказывается, как привести дроби к общему знаменателю и как найти наименьший общий знаменатель. Приведены определения, дано правило приведения дробей к общему знаменателю и рассмотрены практические примеры.
Что такое приведение дроби к общему знаменателю?
Обыкновенные дроби состоят из числителя — верхней части, и знаменателя — нижней части. Если дроби имеют одинаковый знаменатель, говорят, что они приведены к общему знаменателю. Например, дроби 1114, 1714, 914 имеют одинаковый знаменатель 14. Другими словами, они приведены к общему знаменателю.
Если же дроби имеют разные знаменатели, то их всегда можно привести к общему знаменателю при помощи нехитрых действий. Чтобы сделать это, нужно числитель и знаменатель умножить на определенные дополнительные множители.
Очевидно, что дроби 45 и 34 не приведены к общему знаменателю. Чтобы это сделать, нужно с использованием дополнительных множителей 5 и 4 привести их к знаменателю 20. Как именно сделать это? Умножим числитель и знаменатель дроби 45 на 4, а числитель и знаменатель дроби 34 умножим на 5. Вместо дробей 45 и 34 получим соответственно 1620 и 1520.
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю — это умножение числителей и знаменателей дробей на такие множители, что в результате получаются идентичные дроби с одинаковым знаменателем.
Общий знаменатель: определение, примеры
Что такое общий знаменатель?
Общий знаменатель
Общий знаменатель дробей — это любое положительное число, которое является общим кратным всех данных дробей.
Другими словами, общим знаменателем какого-то набора дробей будет такое натуральное число, которое без остатка делится на все знаменатели этих дробей.
Ряд натуральных чисел бесконечен, и поэтому, согласно определению, каждый набор обыкновенных дробей имеет бесконечное множество общих знаменателей. Иначе говоря, существует бесконечно много общих кратных для всех знаменателей исходного набора дробей.
Общий знаменатель для нескольких дробей легко найти, пользуясь определением. Пусть есть дроби 16 и 35. Общим знаменателем дробей будет любое положительное общее кратное для чисел 6 и 5. Такими положительными общими кратными являются числа 30, 60, 90, 120, 150, 180, 210 и так далее.
Рассмотрим пример.
Пример 1. Общий знаменатель
Можно ди дроби 13, 216, 512 привести к общему знаменателю, который равен 150?
Чтобы выяснить, так ли это, нужно проверить, является ли 150 общим кратным для знаменателей дробей, то есть для чисел 3, 6, 12. Другими словами, число 150 должно без остатка делиться на 3, 6, 12. Проверим:
150÷3=50, 150÷6=25, 150÷12=12,5
Значит, 150 не является общим знаменателем указанных дробей.
Наименьший общий знаменатель
Наименьшее натуральное число из множества общих знаменателей какого-то набора дробей называется наименьшим общим знаменателем.
Наименьший общий знаменатель
Наименьший общий знаменатель дробей — это наименьшее число среди всех общих знаменателей этих дробей.
Наименьший общий делитель данного набора чисел — это наименьшее общее кратное (НОК). НОК всех знаменателей дробей является наименьшим общим знаменателем этих дробей.
Как найти наименьший общий знаменатель? Его нахождение сводится к нахождению наименьшего общего кратного дробей. Обратимся к примеру:
Пример 2. Найти наименьший общий знаменатель
Нужно найти наименьший общий знаменатель для дробей 110 и 12728.
Ищем НОК чисел 10 и 28. Разложим их на простые множители и получим:
10=2·528=2·2·7НОК(15, 28)=2·2·5·7=140
Как привести дроби к наименьшему общему знаменателю
Существует правило, которое объясняет, как привести дроби к общему знаменателю. Правило состоит из трех пунктов.
Правило приведения дробей к общему знаменателю
- Найти наименьший общий знаменатель дробей.
- Для каждой дроби найти дополнительный множитель. Чтобы найти множитель нужно наименьший общий знаменатель разделить на знаменатель каждой дроби.
- Умножить числитель и знаменатель на найденный дополнительный множитель.
Рассмотрим применение этого правила на конкретном примере.
Пример 3. Приведение дробей к общему знаменателю
Есть дроби 314 и 518. Приведем их к наименьшему общему знаменателю.
По правилу, сначала найдем НОК знаменателей дробей.
14=2·718=2·3·3НОК(14, 18)=2·3·3·7=126
Вычисляем дополнительные множители для каждой дроби. Для 314 дополнительный множитель находится как 126÷14=9, а для дроби 518 дополнительный множитель будет равен 126÷18=7.
Умножаем числитель и знаменатель дробей на дополнительные множители и получаем:
3·914·9=27126, 5·718·7=35126.
Приведение нескольких дробей к наименьшему общему знаменателю
По рассмотренному правилу к общему знаменателю можно приводить не только пары дробей, но и большее их количество.
Приведем еще один пример.
Пример 4. Приведение дробей к общему знаменателю
Привести дроби 32, 56,38 и 1718 к наименьшему общему знаменателю.
Вычислим НОК знаменателей. Находим НОК трех и большего количества чисел:
НОК(2, 6)=6НОК(6, 8)=24НОК(24, 18)=72НОК(2, 6, 8, 18)=72
Далее вычислим дополнительные множители для каждой дроби.
Для 32 дополнительный множитель равен 72÷2= 36, для 56 дополнительный множитель равен 72÷6= 12, для 38 дополнительный множитель равен 72÷8= 9, наконец, для 1718 дополнительный множитель равен 72÷18= 4.
Умножаем дроби на дополнительные множители и переходим к наименьшему общему знаменателю:
32·36=1087256·12=607238·9=27721718·4=6872
Как привести дробь к наименьшему общему знаменателю (пример)

27 июля 2011
Изначально я хотел включить методы приведения к общему знаменателю в параграф «Сложение и вычитание дробей». Но информации оказалось так много, а важность ее столь велика (ведь общие знаменатели бывают не только у числовых дробей), что лучше изучить этот вопрос отдельно.
Итак, пусть у нас есть две дроби с разными знаменателями. А мы хотим сделать так, чтобы знаменатели стали одинаковыми. На помощь приходит основное свойство дроби, которое, напомню, звучит следующим образом:
Дробь не изменится, если ее числитель и знаменатель умножить на одно и то же число, отличное от нуля.
Таким образом, если правильно подобрать множители, знаменатели у дробей сравняются — этот процесс называется приведением к общему знаменателю. А искомые числа, «выравнивающие» знаменатели, называются дополнительными множителями.
Для чего вообще надо приводить дроби к общему знаменателю? Вот лишь несколько причин:
- Сложение и вычитание дробей с разными знаменателями. По-другому эту операцию никак не выполнить;
- Сравнение дробей. Иногда приведение к общему знаменателю значительно упрощает эту задачу;
- Решение задач на доли и проценты. Процентные соотношения являются, по сути, обыкновенными выражениями, которые содержат дроби.
Есть много способов найти числа, при умножении на которые знаменатели дробей станут равными. Мы рассмотрим лишь три из них — в порядке возрастания сложности и, в некотором смысле, эффективности.
Умножение «крест-накрест»
Самый простой и надежный способ, который гарантированно выравнивает знаменатели. Будем действовать «напролом»: умножаем первую дробь на знаменатель второй дроби, а вторую — на знаменатель первой. В результате знаменатели обеих дробей станут равными произведению исходных знаменателей. Взгляните:
Задача. Найдите значения выражений:
В качестве дополнительных множителей рассмотрим знаменатели соседних дробей. Получим:
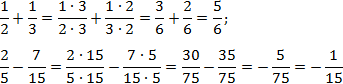
Да, вот так все просто. Если вы только начинаете изучать дроби, лучше работайте именно этим методом — так вы застрахуете себя от множества ошибок и гарантированно получите результат.
Единственный недостаток данного метода — приходится много считать, ведь знаменатели умножаются «напролом», и в результате могут получиться очень большие числа. Такова расплата за надежность.
Метод общих делителей
Этот прием помогает намного сократить вычисления, но, к сожалению, применяется он достаточно редко. Метод заключается в следующем:
- Прежде, чем действовать «напролом» (т.е. методом «крест-накрест»), взгляните на знаменатели. Возможно, один из них (тот, который больше), делится на другой.
- Число, полученное в результате такого деления, будет дополнительным множителем для дроби с меньшим знаменателем.
- При этом дробь с большим знаменателем вообще не надо ни на что умножать — в этом и заключается экономия. Заодно резко снижается вероятность ошибки.
Задача. Найдите значения выражений:
Заметим, что 84 : 21 = 4; 72 : 12 = 6. Поскольку в обоих случаях один знаменатель делится без остатка на другой, применяем метод общих множителей. Имеем:
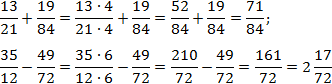
Заметим, что вторая дробь вообще нигде ни на что не умножалась. Фактически, мы сократили объем вычислений в два раза!
Кстати, дроби в этом примере я взял не случайно. Если интересно, попробуйте сосчитать их методом «крест-накрест». После сокращения ответы получатся такими же, но работы будет намного больше.
В этом и состоит сила метода общих делителей, но, повторюсь, применять его можно лишь в том случае, когда один из знаменателей делится на другой без остатка. Что бывает достаточно редко.
Метод наименьшего общего кратного
Когда мы приводим дроби к общему знаменателю, мы по сути пытаемся найти такое число, которое делится на каждый из знаменателей. Затем приводим к этому числу знаменатели обеих дробей.
Таких чисел очень много, и наименьшее из них совсем не обязательно будет равняться прямому произведению знаменателей исходных дробей, как это предполагается в методе «крест-накрест».
Например, для знаменателей 8 и 12 вполне подойдет число 24, поскольку 24 : 8 = 3; 24 : 12 = 2. Это число намного меньше произведения 8 · 12 = 96.
Наименьшее число, которое делится на каждый из знаменателей, называется их наименьшим общим кратным (НОК).
Обозначение: наименьшее общее кратное чисел a и b обозначается НОК(a; b). Например, НОК(16; 24) = 48; НОК(8; 12) = 24.
Если вам удастся найти такое число, итоговый объем вычислений будет минимальным. Посмотрите на примеры:
Задача. Найдите значения выражений:
Заметим, что 234 = 117 · 2; 351 = 117 · 3. Множители 2 и 3 взаимно просты (не имеют общих делителей, кроме 1), а множитель 117 — общий. Поэтому НОК(234; 351) = 117 · 2 · 3 = 702.
Аналогично, 15 = 5 · 3; 20 = 5 · 4. Множители 3 и 4 взаимно просты, а множитель 5 — общий. Поэтому НОК(15; 20) = 5 · 3 · 4 = 60.
Теперь приведем дроби к общим знаменателям:
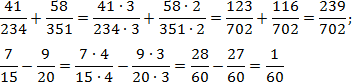
Обратите внимание, насколько полезным оказалось разложение исходных знаменателей на множители:
- Обнаружив одинаковые множители, мы сразу вышли на наименьшее общее кратное, что, вообще говоря, является нетривиальной задачей;
- Из полученного разложения можно узнать, каких множителей «не хватает» каждой из дробей. Например, 234 · 3 = 702, следовательно, для первой дроби дополнительный множитель равен 3.
Чтобы оценить, насколько колоссальный выигрыш дает метод наименьшего общего кратного, попробуйте вычислить эти же примеры методом «крест-накрест». Разумеется, без калькулятора. Думаю, после этого комментарии будут излишними.
Не думайте, что таких сложных дробей в настоящих примерах не будет. Они встречаются постоянно, и приведенные выше задачи — не предел!
Единственная проблема — как найти этот самый НОК. Иногда все находится за несколько секунд, буквально «на глаз», но в целом это сложная вычислительная задача, требующая отдельного рассмотрения. Здесь мы не будем этого касаться.
Смотрите также:
- Сложение и вычитание дробей

- Тест к уроку «Что такое числовая дробь» (средний)

- Тест к уроку «Простые проценты» (легкий)

- Пробный ЕГЭ 2012 от 7 декабря. Вариант 4 (без логарифмов)

- Упрощаем решение задач с помощью замены переменной

- Нестандартная задача B5 на площадь круга

Общий знаменатель и дополнительный множитель.
У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:
(frac{17}{5}, frac{1}{5})
Пример разных знаменателей у дробей:
(frac{8}{3}, frac{2}{13})
Как привести к общему знаменателю дроби?
У первой дроби знаменатель равен 3, у второй равен 13. Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.
Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.
(frac{8}{3} = frac{8 times color{red} {13}}{3 times color{red} {13}} = frac{104}{39})
Вторую дробь умножаем на дополнительный множитель 3.
(frac{2}{13} = frac{2 times color{red} {3}}{13 times color{red} {3}} = frac{6}{39})
Мы привели к общему знаменателю дроби:
(frac{8}{3} = frac{104}{39}, frac{2}{13} = frac{6}{39})
Наименьший общий знаменатель.
Рассмотрим еще пример:
Приведем дроби (frac{5}{8}) и (frac{7}{12}) к общему знаменателю.
Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.
Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.
Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.
Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.
(begin{align}&frac{5}{8} = frac{5 times color{red} {3}}{8 times color{red} {3}} = frac{15}{24}\\&frac{7}{12} = frac{7 times color{red} {2}}{12 times color{red} {2}} = frac{14}{24}\\ end{align})
Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ сократить.
Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.
Например:
Приведите дроби (frac{1}{4}) и (frac{9}{16}) к наименьшему общему знаменателю.
Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:
(begin{align}&frac{1}{4} = frac{1 times color{red} {4}}{4 times color{red} {4}} = frac{4}{16}\\&frac{9}{16} = frac{9 times color{red} {1}}{16 times color{red} {1}} = frac{9}{16}\\ end{align})
Вопросы по теме:
Любые ли две дроби можно привести к одному общему знаменателю?
Ответ: да.
К какому знаменателю принято приводить дроби?
Ответ: к наименьшему общему знаменателю.
Пример №1:
Для дроби (frac{1}{2}) запишите равную дробь со знаменателем: а) 12 б) 18 в) 50?
Решение:
а) Число 2 нужно умножить на 6, чтобы получить 12. Следовательно, мы всю дробь умножаем на дополнительный множитель 6.
(frac{1}{2} = frac{1 times color{red} {6}}{2 times color{red} {6}} = frac{6}{12})
б) Число 2 нужно умножить на 9, чтобы получить 18. Следовательно, мы всю дробь умножаем на дополнительный множитель 9.
(frac{1}{2} = frac{1 times color{red} {9}}{2 times color{red} {9}} = frac{9}{18})
в) Число 2 нужно умножить на 25, чтобы получить 50. Следовательно мы всю дробь умножаем на дополнительный множитель 25.
(frac{1}{2} = frac{1 times color{red} {25}}{2 times color{red} {25}} = frac{25}{50})
Ëþáûå 2 äðîáè âîçìîæíî ïðèâåñòè ê îäèíàêîâîìó çíàìåíàòåëþ, ëèáî, ãîâîðÿ äðóãèìè ñëîâàìè, ê îáùåìó çíàìåíàòåëþ. Ïðèâåäåíèå äðîáåé ê îáùåìó çíàìåíàòåëþ çíà÷èò âûðàçèòü äðîáè â îäèíàêîâûõ ÷àñòÿõ åäèíèöû ñ ñîõðàíåíèåì âåëè÷èíû äðîáè.
Êàëüêóëÿòîð äðîáåé îíëàéí. Ñëîæåíèå, âû÷èòàíèå, óìíîæåíèå, äåëåíèå äðîáåé.
Êàëüêóëÿòîð äåñÿòè÷íûõ äðîáåé îíëàéí. Ïåðåâîä äåñÿòè÷íûõ äðîáåé â îáû÷íûå è îáû÷íûõ â äåñÿòè÷íûå.
Îáùèì çíàìåíàòåëåì äðîáåé ìîæåò ñòàòü êàæäîå îáùåå êðàòíîå çíàìåíàòåëåé ýòèõ äðîáåé (ïðèìåð: ïðîèçâåäåíèå çíàìåíàòåëåé). Îí ðàâåí íàèìåíüøåìó îáùåìó êðàòíîìó (ÍÎÊ) çíàìåíàòåëåé ýòèõ äðîáåé. Äðîáü íå èçìåíèòñÿ, åñëè åå ÷èñëèòåëü è çíàìåíàòåëü óìíîæàòü íà îäèíàêîâîå ÷èñëî, íå ðàâíîå íóëþ.
Çà÷åì ïðèâîäÿò äðîáè ê îáùåìó çíàìåíàòåëþ? Íèæå ïðèâåäåíû íåêîòîðûå ïðè÷èíû:
- Ñëîæåíèå è âû÷èòàíèå äðîáåé ñ ðàçíûìè çíàìåíàòåëÿìè. Äðóãèõ ñïîñîáîâ äëÿ âûïîëíåíèÿ ýòîé îïåðàöèè íå ñóùåñòâóåò;
- Ñðàâíåíèå äðîáåé. Èíîãäà ïðèâåäåíèå ê îáùåìó çíàìåíàòåëþ ñèëüíî îáëåã÷àåò âûïîëíåíèå çàäàíèÿ;
- Ðåøåíèå çàäà÷ íà äîëè è ïðîöåíòû. Ïðîöåíòíûå ñîîòíîøåíèÿ ýòî, ïî ñóòè, îáûêíîâåííûå âûðàæåíèÿ, ñîäåðæàùèå äðîáè.
×òîáû ïðèâåñòè äðîáè ê îáùåìó çíàìåíàòåëþ, íåîáõîäèìî:
- íàéòè íàèìåíüøåå îáùåå êðàòíîå (ÍÎÊ) çíàìåíàòåëåé ýòèõ äðîáåé (íàèìåíüøèé îáùèé çíàìåíàòåëü – ÍÎÇ);
- ïîäåëèòü íàèìåíüøèé îáùèé çíàìåíàòåëü (ÍÎÇ) íà çíàìåíàòåëè ýòèõ äðîáåé, òî åñòü, íàéòè êàæäîé äðîáè äîïîëíèòåëüíûé ìíîæèòåëü;
- óìíîæèòü ÷èñëèòåëü è çíàìåíàòåëü êàæäîé äðîáè íà äîïîëíèòåëüíûé ìíîæèòåëü.
Ðàññìîòðèì ïðèìåð:
Ïðèâåñòè äðîáè  ,
,  ê íàèìåíüøåìó îáùåìó çíàìåíàòåëþ (ÍÎÇ).
ê íàèìåíüøåìó îáùåìó çíàìåíàòåëþ (ÍÎÇ).
1. Îïðåäåëèì íàèìåíüøåå îáùåå êðàòíîå (ÍÎÊ) çíàìåíàòåëåé çàäàííûõ äðîáåé – ýòî áóäåò èñêîìûì íàèìåíüøèì îáùèì çíàìåíàòåëåì:
4 = 2 • 2;
6 = 2 • 3;
ÍÎÊ (4 , 6) = 2 • 2 • 3 = 12;
ÍÎÇ (íàèìåíüøèé îáùèé çíàìåíàòåëü) = 12;
2. Ðàçäåëèì íàèìåíüøèé îáùèé çíàìåíàòåëü íà çíàìåíàòåëè çàäàííûõ äðîáåé, òî åñòü íàéäåì äëÿ êàæäîé äðîáè äîïîëíèòåëüíûé ìíîæèòåëü:
äîïîëíèòåëüíûé ìíîæèòåëü äëÿ äðîáè  :
:
12 : 4 = 3;
äîïîëíèòåëüíûé ìíîæèòåëü äëÿ äðîáè  :
:
12 : 6 = 2;
3. Óìíîæèì ÷èñëèòåëü è çíàìåíàòåëü êàæäîé äðîáè íà äîïîëíèòåëüíûé ìíîæèòåëü:
 ,
, 
Äðîáè ïðèâåäåíû ê îáùåìó çíàìåíàòåëþ.
Èíæåíåðíûé êàëüêóëÿòîð | |
| Èíæåíåðíûé êàëüêóëÿòîð âû÷èñëÿåò ñèíóñ, êîñèíóñ, òàíãåíñ, ëîãàðèôì, ýêñïîíåíòó, âîçâåäåíèå â ñòåïåíü è ò.ä. | |
| Èíæåíåðíûé êàëüêóëÿòîð | |
Êàëüêóëÿòîð äðîáåé | |
| Êàëüêóëÿòîð äðîáåé — ñëîæåíèå, âû÷èòàíèå, óìíîæåíèå, äåëåíèå äðîáåé â òîì ÷èñëå ñ öåëûìè ÷èñëàìè. | |
| Êàëüêóëÿòîð äðîáåé | |
Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû: êîðíè, äðîáè, ñòåïåíè, óðàâíåíèÿ, ôèãóðû, ñèñòåìû ñ÷èñëåíèÿ è äðóãèå êàëüêóëÿòîðû. | |
| Ìàòåìàòè÷åñêèå êàëüêóëÿòîðû | |
Êàëüêóëÿòîðû ïî àëãåáðå | |
| Ðåøåíèÿ, ïîäñêàçêè è ó÷åáíèê ëèíåéíîé àëãåáðû îíëàéí (âñå êàëüêóëÿòîðû ïî àëãåáðå). | |
| Êàëüêóëÿòîðû ïî àëãåáðå | |
Îáûêíîâåííûå äðîáè | |
| Ïðàâèëüíûå, íåïðàâèëüíûå, ñìåøàííûå, ñîñòàâíûå, äåñÿòè÷íûå äðîáè, ñîêðàùåíèå, äåëåíèå äðîáåé | |
| Îáûêíîâåííûå äðîáè | |
Ìàòåìàòèêà 4,5,6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ìàòåìàòèêè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ìàòåìàòèêà 4,5,6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
